미적분학

미적분학(微積分學, calculus)은 수학의 한 분야로 극한, 함수, 미분, 적분, 무한급수를 다루는 학문이다. 미분은 도함수라는 정의역에서 미소한 차이에 대한 함수값의 차이 값의 비를 구한다. 그 값은 곡선의 기울기로 해석한다. 또 넓이, 부피, 길이 등은 곡선으로 제한된다. 여기서 "곡선"은 직선을 의미할 수도 있으므로 주의해야 한다. 또 극한을 구하는 과정을 유도하는 무한 과정 또는 궁극점(일반적으로 구하는 값)에 접근해 가는 것과 관련이 있다. 이 2가지 방법은 수학적 해석학의 토대가 되고 있다. 기하학이 모양에 중심을 둔 학문이고 대수학이 연산에 대한 수학이라면, 미적분학은 변화에 중점을 둔 수학이다. 미적분학은 크게 2개의 분야로 분류되는데, 미분과 적분이 바로 그것이다. 미분은 미소적인 변화를 다루는 분야이고, 적분은 미소적인 양의 집적을 다루는 분야이다.

미분의 기하학적 의미를 보면, 특정 함수 그래프의 어떤 점에서 접선, 혹은 접평면을 구하는데 필요한 연산이다. 더 일반적으로, 미분은 원래는 어렵게 정의된 함수를 선형근사해서 다루기 쉬운 형태로 바꾸어 파악하려는 목적을 가지고 있다. 미분은 선형사상이 된다. 그래서 선형 대수학에서 미분가능한 함수들의 선형공간을 다룰 때 중요한 선형사상으로 여겨진다. (단, 다변수 함수의 미분을 선형사상으로 취급하는 방식은 20세기에 들어서부터 확립됐다.) 미분방정식은 이런 사고의 자연스러운 연장 선상에 있다.

적분은 기하학적으로 보면, 곡선 또는 곡면과 좌표축으로 둘러싸인 영역의 면적을 구하는 것에 해당된다.(단, 이때는 절댓값 기호를 씌워서 곡선 또는 곡면을 x축위로 꺾어올렸을때의 상태이다.)(실제 적분의 기하학적인 의미는 y좌표, 즉 길이들의 합이다.) 그러나 적분의 의미는 오랫동안 확실하게 파악되지 못하고 있었다. 적분의 확실한 정의를 내린 사람은 베른하르트 리만이 최초이다. 리만이 생각한 적분을 정식화한 것을 리만 적분이라고 한다. 적분 또한 선형사상이다.

미분과 적분은 완전히 별개의 개념이지만, 밀접한 연관성을 갖는다. 변수가 하나인 경우, 하나가 나머지의 역연산이 된다. 이를 미적분학의 기본정리라고 부른다.

역사

고대 시기

적분을 이끌어내기 위한 몇 가지 아이디어들은 고대에서부터 시작됐지만 이 시대의 방법들은 수학적으로 엄밀하지도 않고 체계적이지 않았다. 모스크바 수학 파피루스(Moscow mathematical papyrus)에서 적분의 목표 중 하나인 부피계산법들이 나와있으나 이것들은 방법으로서 설명이 부족하고 몇 가지는 틀렸다. 고대 그리스에서는 크니도스의 에우독소스(Eudoxus)가 극한의 개념과 유사한 문제의 철저 검토법을 사용했고 아르키메데스는 이 방법을 발전시킨 발견적 교수법이라는 적분과 비슷한 방법을 만들었다. 중국에서는 유휘가 3세기에 원의 넓이를 구하기 위해 크니도스의 에우독소스와 같은 방법을 발명하였다.

중세 시기

14세기에 인도의 수학자들은 일부 삼각함수에 적용할 수 있는 미분과 비슷한 엄격하지 않은 방법을 제시했다. Sangamagrama의 Madhava및 Kerala 천문학 및 수학 학교 에서는 미적분학의 구성 요소를 명시했다. 이러한 구성요소를 포괄하는 완전한 이론은 이제 서구 세계에서 Taylor 계열 또는 무한 계열 근사로 잘 알려져 있다..

근대 시기

프랑스 수학자 피에르 드 페르마는 무한소 오차항이 있어도 등호가 성립된다는 것을 보여주는 adequality 개념을 소개했으며, 미분해서 0이 되는 곳을 구하여서 극대 극소를 찾는 법을 만들었다. 아일랜드 수학자 제임스 그레고리(James Gregory)이 미적분학의 핵심 정리인 미적분학 기본정리의 증명을 출판하였으며, 영국 수학자 아이작 배로(Issac Barrow)가 좀 더 일반적인 경우를 증명하였다. 무한소 미적분과 유한차 미적분의 결합은 두 번째 미적분학 기본정리가 증명되고 2년이 지나서 존 월리스(John Wallis), 아이작 배로(Issac Barrow)와 제임스 그레고리(James Gregory)에 의해 1670년경에 완성됐다.

이후 고트프리트 라이프니츠, 아이작 뉴턴이 당시 알려져 있던 미적분학을 좀 더 체계화하고 발전시켰다.

아이작 뉴턴은 그가 수리물리학 문제를 풀 때 사용했던 이상한 형태의 곱의 미분법, 연쇄법칙, 고계도 미분계수의 개념, 테일러 급수와 해석함수를 공개했다. 하지만 그가 출판물로 낼 때는 그 시대의 수학적 표현방법에 맞게 그의 아이디어와 동등한 의미를 지니는 기하적 표현으로 그의 아이디어를 적어냈다. 뉴턴은 그의 책 자연철학의 수학적 원리에서 거론한 행성의 운동, 회전하는 유체 표면의 모양, 지구의 편평도, 사이클로이드에서 미끄러지는 물체의 운동 같은 문제들을 푸는 데 미적분을 사용했다. 뉴턴은 미적분과 함께 함수의 급수를 실수의 범위로 확장했고 테일러 급수의 원칙들을 이해하고 있었다. 하지만 그는 그가 이뤄낸 모든 발견을 출판하지는 않았고 이 시대에 무한소를 이용한 방법은 여전히 평이 좋지 않았다.

그의 아이디어들은 뉴턴이 자신을 표절했다고 고소한 고트프리트 라이프니츠에 의해서 참된 무한소 미적분으로 체계화됐다. 뉴턴은 그를 표절자로 여겼지만, 현재는 그도 독립적으로 얻은 것임이 밝혀졌다. 그는 무한소를 다루는 규칙들을 명확하게 정리했고 2계도 이상의 미분을 가능하도록 해줬으며 곱의 미분법과 연계법칙을 미분 적분 형태로 모두 만들었다.

앞에서 말했듯이 뉴턴과 라이프니츠는 모두 미적분학에 기여한 자로 인정받고 있다. 하지만 둘의 미적분의 성격은 다르다. 뉴턴은 미적분을 물리학에서 활용한 첫 번째 사람으로, 라이프니츠는 오늘날 사용하는 미적분 표기법의 대부분을 만든 사람으로 여겨진다. 또 라이프니츠는 뉴턴과는 달리 형식을 중시해서 알맞은 표현법을 만들어내는데 며칠을 쓰는 일도 종종 있었다고 한다. 두 사람의 미적분에서 규정한 기본적인 사항들로는 미분과 적분의 법칙들, 2계도 이상에서의 미분, 다항 함수 급수의 근사에 대한 개념들이 있다. (뉴턴과 라이프니츠 이전에 미분과 적분이 역관계라는 미적분학의 기본정리들은 이미 알려져 있었다.)

라이프니츠가 그의 결과를 발표하고 뉴턴이 그의 아이디어에 대해서 권리를 주장하자 수학자들 사이에서는 어떤 사람을 우선권자로 인정을 해야 하느냐는 주제로 큰 논란이 일었다. 뉴턴이 최초로 결과를 이끌어 낸 사람이지만 출판을 한 것은 라이프니츠가 처음이었기 때문이다. 뉴턴은 라이프니츠가 자신이 출판하지 않고 왕립학회에서 공유한 노트들에서 아이디어를 훔쳤다고 주장했다. 이 논란 때문에 영국 수학자들과 유럽 대륙의 수학자들이 오랫동안 갈라지게 되고 이는 영국 수학에 큰 손실을 초래했다. 현재는 뉴턴과 라이프니츠의 논문에 대한 면밀한 조사 덕분에 그들이 독립적으로 결론을 이끌어 냈다는 것이 밝혀졌다. 라이프니츠는 적분에서부터 뉴턴은 미분에서부터 시작해서 결과를 도출해냈다.

이 시대 이후에 수많은 수학자들이 미적분학 발전에 크게 공헌했다. 첫 번째로 가장 성공적이었던 업적 중 하나로 마리아 아녜시가 1748년에 쓴 무한과 유한 분석이 있다.

기초

미적분학에서 기초(foundations)는 정확하고 엄밀한 공리와 정의들의 발전을 말한다. 초기 미적분학에서 사용한 무한소는 엄밀하지 않은 것으로 생각되었기에 많은 수학자들에게 특히 미셸 롤과 조지 버클리(George Berkeley)에게 맹렬하게 비난 받았다. 버클리는 그가 1734년에 출판한 《해석학자》(영어: The Analyst)라는 책에서 무한소를 ‘사라진 값들의 유령’(영어: the Ghosts of departed quantities)이라고 묘사했다. 미적분학의 엄밀한 기초를 도출해내는 일은 여러 수학자들이 제공했고 오늘날까지도 연구활동이 있는 분야다.

콜린 매클로린(Colin Maclaurin)을 포함한 다수의 수학자들이 무한소의 사용이 정당하는 것을 증명하려고 시도했지만 그것은 150년이 지나서야 오귀스탱 루이 코시와 카를 바이어슈트라스에 의해서 증명됐고 무한소의 의미가 극히 작은 값이라는 관념을 막을 방법을 찾았다. 이것이 미분과 적분을 위한 기초를 놓았다. 코시의 필기에서 무한소의 형태로 적혀진 연속의 정의와 극한의 (ε-δ) 정의의 원형 등의 기초에 접근하기 위한 다양한 방법을 찾을 수 있다. 코시의 업적에서 바이어슈트라스는 극한의 정의를 공식화 시키고 무한소의 개념을 없애버린다. 바이어슈트라스의 작업에 따라서 미적분학은 무한소가 아닌 극한에 기초하는 것이 일반적이게 됐다. 베른하르트 리만은 바이어슈트라스의 개념을 사용해서 적분의 정확한 개념을 만들었다. 그리고 이 발견의 기간 동안 미적분학의 아이디어들은 유클리드 공간과 복소평면에서 일반화됐다. 현대 수학에서 미적분학의 기초는 미적분학의 정리에 대한 완전한 정의와 증명들을 포함하는 실해석 분야에 포함되어 있고 미적분학의 범위는 엄청나게 확대됐다. 앙리 르베그는 측도론을 만들어서 거의 모든 함수에서 적분을 가능하게 했다. 로랑 슈바르츠는 어떤 함수도 미분시킬 수 있는 분포 이론을 만들었다.

일반적으로 극한의 개념을 미적분학의 기초로 두지만 극한이 미적분학의 기초에 대한 유일한 접근법은 아니다. 에이브러햄 로빈슨(Abraham Robinson)의 비표준해석학이 대안책이다. 1960년대에 만들어진 로빈슨의 접근법은 미적분학 초창기에 사용했던 개념인 무한소와 무한수로 실수체계를 늘린 체계를 사용한다. 그 결과로 나온 수를 초실수라고 부른다. 초실수는 미적분학의 일반적인 법칙들을 라이프니츠의 방식처럼 이끌어 낼 수 있다.

함수

함수의 정의

함수 $f$ 란 집합 $D$안에 있는 원소 $x$가 집합 $E$에 있는 정확히 한 원소, $f(x)$에 대응되는 규칙을 말한다. 여기서 집합 $D$는 정의역이라하고 $E$는 공역이라고 한다. 또한 정의역에 있는 임의의 수를 나타내는 기호를 독립변수, 공역에 있는 원소를 나타내는 기호를 종속변수라고 한다.

함수의 표현방법

함수를 표현하는 방법에는 말로 설명하는 방법, 표를 이용하는 방법, 그래프를 이용하는 방법, 대수학적 식으로 표현하는 방법 등이 있다.

극한

극한의 정의

$\lim _{x\to a}f(x)=L$는 $x$가 $a$로 다가갈 때 $f(x)$가 $L$로 다가간다는 것이다. 극한에는 좌극한과 우극한이 존재하는데 좌극한이란 $x$가 $a$보다 작은 곳에서 $a$로 다가갈 때 $f(x)$가 다가가는 값을 의미하고 우극한은 반대로 $x$가 $a$보다 큰 곳에서 다가간다. 좌극한과 우극한은 기호로 각각 $\lim _{x\to a^{-}}f(x)=L$, $\lim _{x\to a^{+}}f(x)=L$라고 표시한다. 극한값이 $L$라는 것과 좌극한과 우극한 모두 $L$라는 것은 필요충분조건이다.$\lim _{x\to a}f(x)=\infty$는 $x$가 $a$로 다가갈 때 $f(x)$는 무한히 커진다는 것이고 $\lim _{x\to a}f(x)=-\infty$는 무한히 작아진다는 것이다.

엡실론-델타 논법

 이 부분의 본문은 엡실론-델타 논법입니다.

극한의 더 정확한 수학적 정의는 엡실론-델타 논법이다. $\lim _{x\to a}f(x)=L$는 모든 양수 $\epsilon$에 대해 만약 $0<|x-a|<\delta$ 면 $|f(x)-L|<\varepsilon$인 $\delta$가 존재한다는 것이다. 이 말을 기호로 나타내면 다음과 같다.

$\forall \varepsilon >0\ \ \exists \,\delta \ \ s.t\ \ if\ \ 0<|x-a|<\delta \ \ then\ \ |f(x)-L|<\varepsilon$

이 방법을 이용하여 여러 가지 극한들을 정의하면 다음과 같다.

• $\lim _{x\to a^{-}}f(x)=L$: $\forall \varepsilon >0\ \ \exists \delta \ \ s.t\ \ if\ \ a-\delta <x<a\ \ then\ \ |f(x)-L|<\varepsilon$
• $\lim _{x\to a^{+}}f(x)=L$: $\forall \varepsilon >0\ \ \exists \delta \ \ s.t\ \ if\ \ a<x<a+\delta \ \ then\ \ |f(x)-L|<\varepsilon$
• $\lim _{x\to a}f(x)=\infty$: $\forall M>0\ \ \exists \delta \ \ s.t\ \ if\ 0<|x-a|<\delta \ \ then\ \ f(x)>M$
• $\lim _{x\to a}f(x)=-\infty$: $\forall N<0\ \ \exists \delta \ \ s.t\ \ if\ 0<|x-a|<\delta \ \ then\ \ f(x)<N$
• $\lim _{x\to \infty }f(x)=L$: $\forall \epsilon >0\ \ \exists N\ \ s.t\ \ if\ x>N\ \ then\ \ |f(x)-L|<\epsilon$
• $\lim _{x\to -\infty }f(x)=L$: $\forall \epsilon >0\ \ \exists N\ \ s.t\ \ if\ x<N\ \ then\ \ |f(x)-L|<\epsilon$
• $\lim _{x\to \infty }f(x)=\infty$: $\forall M>0\ \ \exists N\ \ s.t\ \ if\ x>N\ \ then\ \ f(x)>M$

극한의 성질

$c$가 상수이고 $\lim _{x\to a}f(x)$ 와 $\lim _{x\to a}g(x)$가 존재할 때 다음 성질들을 만족한다.

• $\lim _{x\to a}[f(x)+g(x)]=\lim _{x\to a}f(x)+\lim _{x\to a}g(x)$
• $\lim _{x\to a}[f(x)-g(x)]=\lim _{x\to a}f(x)-\lim _{x\to a}g(x)$
• $\lim _{x\to a}[cf(x)]=c\lim _{x\to a}f(x)$
• $\lim _{x\to a}[f(x)g(x)]=\lim _{x\to a}f(x)\lim _{x\to a}g(x)$
• $\lim _{x\to a}\left[{\frac {f(x)}{g(x)}}\right]={\frac {\lim _{x\to a}f(x)}{\lim _{x\to a}g(x)}}\ \ if\ \ \lim _{x\to a}g(x)\neq 0$
• $\lim _{x\to a}[f(x)]^{n}=[\lim _{x\to a}f(x)]^{n}$

극한에 관한 정리

• 만약 $a$ 근처 $x$에서 $f(x)\leq g(x)$이고 $f,g$ 둘다 $a$에서 극한값이 존재한다면 $\lim _{x\to a}f(x)\leq \lim _{x\to a}g(x)$이다.
• 샌드위치 정리(조임 정리): 만약 $a$ 근처 $x$에서 $f(x)\leq g(x)\leq h(x)$이고 세 함수 모두 $a$에서 극한값이 존재하고 $\lim _{x\to a}f(x)=\lim _{x\to a}h(x)=L$이라면 $\lim _{x\to a}g(x)=L$이다.

연속

 이 부분의 본문은 연속함수입니다.

 함수의 극한 문서를 참고하십시오.

함수 $f(x)$가 $x=a$에서 연속

$\mathbb {R} \to \mathbb {R}$에서 정의된 함수 $f(x)$가 다음의 조건을 만족할 때 $f(x)$는 $x=a$인 점에서 연속이라고 한다. ($a\in \mathbb {R}$)

• $x=a$에서 함숫값 $f(a)$가 존재한다.
• $x=a$에서 극한값 $\lim _{x\to a}f(x)$가 존재한다.
• $x=a$에서 함숫값과 극한값이 일치한다.

함수 $f(x)$가 연속

함수 $f(x)$가 정의역에 존재하는 모든 $x$에서 연속일 때, $f(x)$는 연속함수라고 한다.

정의역 이외의 $x$에 대해서 불연속이더라도, 함수의 연속성에는 영향을 미치지 않는다. 예를 들어, $f(x)={\frac {1}{x}}$은 $x=0$ 이외의 모든 점에서 연속이다. $x=0$에서는 함숫값이 정의되지 않아 불연속이지만, $0$은 정의역에 있지 않는 수이므로 함수 $f(x)$는 연속함수이다.

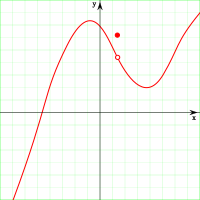
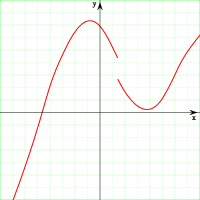
함수의 그래프	연속성
	연속이다.
	함숫값이 존재하지 않으므로 불연속이다.
	함숫값과 극한값이 일치하지 않으므로 불연속이다.
	좌극한값과 우극한값이 일치하지 않아 극한값이 존재하지 않으므로 불연속이다.

균등연속(Uniform Continuity)

함수 f(x)가 모든 정의역에서 연속이면, 정의역의 모든점 $x_{0}$에 대해서 ε-δ 논법에 의해 모든 ε>0에 대해 0<|$x-x_{0}$|<δ를 만족하는 x가 |$f(x)-f(x_{0})$|<ε가 되게 하는 δ>0이 존재한다. 만약 모든 $x_{0}$에 대해서 δ가 같다면, 즉, δ가 $x_{0}$에 변화에 따르지 않고 오직 ε의 변화에만 따른다면, 이 함수 f(x)가 균등연속(Uniformly continuous)이라고 한다.

제거 가능한 불연속성

제거 가능한 불연속성을 지니는 함수

함수 f(x)가 $x=x_{0}$에서 불연속이지만 $f(x_{0})$를 적절히 정했을 때 연속이 될 수 있다면, $f(x)$는 $x=x_{0}$에서 제거 가능한 불연속성을 지닌다고 표현한다.

예를 들어 $f(x)={\frac {\sin x}{x}}$라면, $x=0$인 점에서 함숫값이 정의되지 않아 불연속이다. 그러나 $\lim _{x\to 0}f(x)=1$로 극한값이 존재하므로 만약 $f(0)=1$로 함숫값을 정하면 불연속성이 제거될 수 있다. 따라서 함수 $f(x)$는 x=0인 점에서 제거 가능한 불연속성을 지닌다.

미분

도함수

그래프 $y=f(x)$에서 점$P(a,f(a))$을 통과하는 접선은 기울기 $m=\lim _{x\to a}{\frac {f(x)-f(a)}{x-a}}$를 가진다. 여기서 $x-a=h$라고 하면 $m=\lim _{h\to 0}{\frac {f(a+h)-f(a)}{h}}$가 된다. 함수 $f(x)$의 도함수 $f^{'}(x)$란 $m=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}$를 의미한다. 도함수 표현법에는 $f'(x)=y'={\frac {dy}{dx}}={\frac {df}{dx}}={\frac {d}{dx}}f(x)=Df(x)=D_{x}f(x)$ 등이 있다. 도함수를 한번 더 미분한 것을 이계도함수라고 한다. 이계도함수의 표현법에는 $y''=f''(x)={\frac {d}{dx}}({\frac {dy}{dx}})={\frac {d^{2}y}{dx^{2}}}$ 등이 있다.이계도함수를 또 한번 더 미분한 것을 삼차도함수라고 하고 이것은 $y'''=f'''(x)={\frac {d}{dx}}\left({\frac {d^{2}y}{dx^{2}}}\right)={\frac {d^{3}y}{dx^{3}}}$ 등으로 표현한다. $f$를 $n$번 미분한 것은 $y^{(n)}=f^{(n)}(x)={\frac {d^{n}y}{dx^{n}}}$ 등으로 표현한다.

미분 가능성

함수 $f$가 $a$에서 미분 가능하다는 말은 $f'(a)$가 존재한다는 것이다. 구간$(a,b),(a,\infty ),(-\infty ,a),(-\infty ,\infty )$에서 미분가능하다는 말은 구간 내의 모든점에서 미분가능하다는 것이다. 함수 $f$가 점 $a$에서 미분 가능하다는 말은 $a$에서 연속하다는 것이다. 미분 불가능한 경우에는 좌미분계수$\left(m=\lim _{h\to 0^{-}}{\frac {f(x+h)-f(a)}{x}}\right)$와 우미분계수$\left(m=\lim _{h\to 0^{+}}{\frac {f(x+h)-f(a)}{x}}\right)$값이 다르거나 불연속하거나 수직 접선을 가지고 있다는 것이다. 수직접선이란 $\lim _{x\to a}|f'(x)|=\infty$일 때 $a$에서 수직 접선을 가진다.

미분의 성질

$c$는 상수이고 $f,g$는 미분 가능할 때 다음을 만족한다.

• ${\frac {d}{dx}}(c)=0$
• ${\frac {d}{dx}}(x^{n})=nx^{n-1}$
• $(cf)'=cf'$
• $(f+g)'=f'+g'$
• $(f-g)'=f'-g'$
• $(fg)'=f'g+g'f$
• $\left({\frac {f}{g}}\right)'={\frac {gf'-fg'}{g^{2}}}$

삼각함수의 미분

$\lim _{\theta \to 0}{\frac {\sin \theta }{\theta }}=1$이다. 이것을 이용하여 삼각함수의 미분을 할 수 있다. 삼각함수들의 미분은 다음과 같다.

• $(\sin x)'=\cos x$
• $(\cos x)'=-\sin x$
• $(\tan x)'=\sec ^{2}x$
• $(\csc x)'=-\csc x\cot x$
• $(\sec x)'=\sec x\tan x$
• $(\cot x)'=-\csc ^{2}x$

연쇄법칙

$g$가 $x$에서 미분가능하고 $f$가 $g(x)$에서 미분가능하면 $F(x)=f(g(x))$는 $x$에서 미분가능하고 $F'(x)=f'(g(x))g'(x)$로 표현된다. 이것을 다른방식으로 표현하면 $y=f(u)$와 $u=g(x)$가 미분가능한 함수면 ${\frac {dy}{dx}}={\frac {dy}{du}}{\frac {du}{dx}}$이다.

음함수 미분법

일반적으로 함수는 $y=f(x)$로 표현된다. 하지만 $x^{2}+y^{2}=25$ 나 $x^{3}+y^{3}=xy$와 같이 표현되는 음함수도 존재한다. 이런 함수를 미분할 때는 이 함수를 $y=f(x)$형태로 바꿀 필요 없이 음함수 미분법을 사용하면 된다. 이 방법은 양변을 모두 $x$에 대하여 미분을 한 뒤, $y'$에 대한 방정식을 풀면 된다. 예를 들어 $x^{2}+y^{2}=25$는 양변을 $x$로 미분하면 $2x+2yy'=0$가 돼서 $y'=-{\frac {x}{y}}$가 된다.

지수, 로그 함수의 미분

지수함수 $y=a^{x}$를 정의를 이용해 미분하면 $y'=a^{x}\lim _{h\to 0}{\frac {a^{h}-1}{h}}$이다. 이때 $f'(0)=\lim _{h\to 0}{\frac {a^{h}-1}{h}}$이므로 $f'(x)=f'(0)\,a^{x}$이다. 이때 $f'(0)=1$이 되는 $a$를 $e$라고 한다. 즉, $\lim _{h\to 0}{\frac {e^{h}-1}{h}}=1$이고 $(e^{x})'=e^{x}$이다.$a^{y}=x$일 때, $\log _{a}{x}=y$라고 정의한다. 이때 $a$를 밑이라고 하는데 밑이 $e$ 인 로그를 자연로그라고하고 $\ln$라고 표현한다. 즉, $\log _{e}{x}=\ln x$이다. $y=\ln x$를 $e^{y}=x$임을 이용하여 미분하면 $(\ln x)'={\frac {1}{x}}$임을 알 수 있다. 이 자연로그의 미분을 이용하여 일반적인 밑을 가지는 지수, 로그 함수의 미분을 구하면 다음과 같다.

• $(a^{x})'=a^{x}\ln a$
• $(\log _{a}{x})'={\frac {1}{x\ln a}}$

적분

역도함수(부정적분)

모든 $x\in I$에 대하여 $F'(x)=f(x)$일 때 함수 $F$를 구간 $I$에서의 $f$의 역도함수(부정적분)라고 한다. 여기서 F가 f의 부정적분이면 일반적으로 F+C도 f의 부정적분이다. 여기서 C는 임의의 상수이다.

정적분

함수 f가 구간 [a,b]에서 정의된 연속함수 일 때, 구간 [a,b]를 동일한 n개의 폭 $\Delta _{x}={\frac {b-a}{n}}$으로 분할하여, 이 n개의 부분구간들의 끝점들을 $x_{0},x_{1},...x_{n}$이라하자. $[x_{i-1},x_{i}]$에 속하도록 표본점 ${x_{i}}^{*}$을 잡자. 이 때 $\lim _{n\to \infty }\sum _{k=1}^{n}f(x_{k})\Delta x$가 존재하면, 그 값을 a로부터 b까지의 f의 정적분$\int _{a}^{b}f(x)dx$이라고 하고, 함수 f는 구간 [a,b]에서 적분 가능하다고 한다. 이 때 표본점은 각구간의 끝점 또는 중점으로 잡는다. 일반적으로 함수f가 구간 [a,b]에서 유한개의 불연속점을 가지면 f가 구간[a,b]에서 적분 가능하다.

정적분의 성질

1. $\int _{a}^{b}f(x)\,dx=-\int _{b}^{a}f(x)\,dx$
2. $\int _{a}^{b}cf(x)\,dx=c\int _{a}^{b}f(x)\,dx$ (단, $c$는 임의의 실수)
3. $\int _{a}^{b}(f(x)+g(x))\,dx=\int _{a}^{b}f(x)\,dx+\int _{a}^{b}g(x)\,dx$
4. $\int _{a}^{c}f(x)\,dx+\int _{c}^{b}f(x)\,dx=\int _{a}^{b}f(x)\,dx$
5. $a\leq x\leq b$인 $x$에 대해서 $f(x)\geq 0$이면 $\int _{a}^{b}f(x)\,dx\geq 0$이다.
6. $a\leq x\leq b$인 $x$에 대해서 $f(x)\geq g(x)$이면 $\int _{a}^{b}f(x)\,dx\geq \int _{a}^{b}g(x)\,dx$이다.
7. $a\leq x\leq b$인 $x$에 대해서 $m\leq f(x)\leq M$이면 $m(b-a)\leq \int _{a}^{b}f(x)\,dx\leq M(b-a)$이다.
8. $a\leq b$이면 $\left\vert \,\int _{a}^{b}f(x)dx\,\right\vert \leq \int _{a}^{b}\ |f(x)|dx$

미적분학의 기본정리

함수 $f$가 구간 $[\,a,\,b\,]$에서 연속이면, $g(x)=\int _{a}^{x}f(t)dt$, $a\leq x\leq b$로 정의된 함수 $g$는 $[\,a,\,b\,]$에서 연속이고 $(\,a,\,b\,)$에서 미분가능하며, $g'(x)=f(x)$이다.

증명:

$x$와 $x+h$가 $(\,a,\,b\,)$안에 있다고 하면 $${\begin{alignedat}{2}g(x+h)-g(x)&=\int _{a}^{x+h}\,f(t)\,dt-\int _{a}^{x}\,f(t)\,dt\\&=\int _{x}^{x+h}f(t)dt\end{alignedat}}$$ 따라서 $h\neq 0$인 $h$에 대해 $${\frac {g(x+h)-g(x)}{h}}={\frac {1}{h}}\int _{x}{x+h}\,f(t)\,dt\,\,\,\cdots \cdots \,\,\,(a)$$이다. 이제 $h>0$임을 가정하자. 극값정리(${\text{Extreme Value Theory}}$에 의해) $f(u)=m$이고 $f(v)=M$인 $u,\,v$가 $[\,x,\,x+h\,]$안에 존재한다. ($m,\,M$은 각각 함수 $f$의 $[\,x,\,x+h\,]$에서의 최솟값과 최댓값) 따라서$$mh\leq \int _{x}^{x+h}\,f(t)dt\leq Mh$$이다. $(a)$에 의해 $$f(u)\leq {\frac {g(x+h)-g(x)}{h}}\leq f(v)$$이고, $(f(u)=m,\,f(v)=M)$, $h<0$인 경우도 비슷한 방법으로 이 부등식을 얻을 수 있다. $h$가 $0$에 가까워질때, $u,\,v$가 $[\,x,\,x+h\,]$안에 있으므로 $u,\,v$는 $x$에 근접하게 된다. 따라서$$\lim _{h\to 0}f(u)=\lim _{h\to 0}f(v)=f(x)$$이다. 그러므로 압축정리에 의해서(${\text{Squeeze Theorem}}$)$$\lim _{h\to 0}{\frac {g(x+h)-g(x)}{h}}=f(x)$$이다.

함수 $f$가 닫힌 구간 $[\,a,\,b\,]$에서 연속이면, $\int _{a}^{b}f(x)dx=F(b)-F(a)$이다.
여기에서 $F$는 $f$의 임의의 역도함수, 즉 $F'=f$이다.

증명:
$g(x)=\int _{a}^{x}f(t)dt$로 놓으면 위의 기본정리에 의해 $g'(x)=f(x)$이다. $f$의 임의의 도함수 $F$는 $g$와 상수만큼 차이가 있다. $F(x)=g(x)+C$ 여기서 C는 상수라고 하자. 따라서 $${\begin{aligned}F(b)-F(a)&=[g(b)+C]-[g(a)+c]\\&=g(b)-g(a)=g(b)\\&=\int _{a}^{b}f(t)dt\end{aligned}}$$이다.

치환 법칙

함수 $u=g(x)$가 미분 가능하고, 그 치역이 구간 I이며 함수 f가 구간 I에서 연속이면,
$\int _{}^{}f(g(x))g'(x)dx=\int _{}^{}f(u)du$이다.

정적분에 대해 변형시키면,
함수 g'이 [a,b]에서 연속이고, 함수 f가 $u=g(x)$의 치역에서 연속이면,
$\int _{a}^{b}f(g(x))g'(x)dx=\int _{g(a)}^{g(b)}f(u)du$이다.

부분적분법

 이 부분의 본문은 부분적분입니다.

두 미분가능한 연속 함수 $f(x)$와 $g(x)$에 대해서, 적분 구간이 $[a,b]$ 일 때, 부분적분법은 다음과 같이 표현할 수 있다.

$\int _{a}^{b}f(x)g'(x)\,dx=\left[f(x)g(x)\right]_{a}^{b}-\int _{a}^{b}f'(x)g(x)\,dx$

이때 우변의 첫째 항은 다음을 나타낸다.

$\left[f(x)g(x)\right]_{a}^{b}=f(b)g(b)-f(a)g(a).$

이 법칙은 다음과 같이 미분의 곱셈 법칙과 미적분학의 기본정리로 증명할 수 있다.

$f(b)g(b)-f(a)g(a)\,$	$=\int _{a}^{b}{\frac {d}{dx}}(f(x)g(x))\,dx$
	$=\int _{a}^{b}f'(x)g(x)\,dx+\int _{a}^{b}f(x)g'(x)\,dx$

부정적분의 경우에는 다음과 같다.

$\int f(x)g'(x)\,dx=f(x)g(x)-\int g(x)f'(x)\,dx$

또는, 짧게 줄여서 다음과 같이 표현하기도 한다.

$\int u\,dv=uv-\int v\,du$

여기서, $u=f(x),\ v=g(x)$이고, $du=f'(x)dx,\ dv=g'(x)dx$이다.

넓이

[a,b]안의 모든 x에 대하여 f,g가 연속이고, $f(x)$≥$g(x)$일 때, 곡선$y=f(x)$,$y=g(x)$와 직선 $x=a$,$x=b$로 둘러싸인 영역의 넓이 A는
$A=\int _{a}^{b}[f(x)-g(x)]dx$로 정의된다.

부피

S를 $x=a$와 $x=b$에 놓인 입체도형이라 하자. x를 지나고 x축에 수직인 평면 P_x에 있는 S의 절단면의 넓이가 A(x)이고, A가 연속이라면 S의 부피(V)는
$V=\int _{a}^{b}A(x)dx$이다.

회전체의 경우, 위의 방법으로는 부피를 구하기 어려운 경우가 많다. 회전체의 부피의 경우, 아래와 같은 방법을 이용한다.
곡선 $y=f(x)$와 $x=a$및 $x=b$로 둘러싸인 영역을 $y$축을 둘레로 회전시킬 때 생기는 회전체의 부피는 다음과 같다.
$V=\int _{a}^{b}2\pi xf(x)dx$

속도와 거리

수직선 위를 움직이는 점 P의 시각 $t$에서의 속도가 $v(t)$이고, 시각 $t=a$에서의 위치가 $x_{0}$일 때, 다음이 성립한다.

1. 시각 $t$에서 점 P의 위치 $x$는 $x=x_{0}+\int _{a}^{t}v(t)dt$
2. 시각 $t=a$에서 $t=b$까지 점 P의 위치의 변화량은 $\int _{a}^{b}v(t)dt$
3. 시각 $t=a$에서 $t=b$까지 점 P가 움직인 거리 s는 $s=\int _{a}^{b}|v(t)|dt$

좌표평면 위를 움직이는 점 P의 시각 $t$에서의 위치 $(x,y)$가 $x=f(t)$, $y=g(t)$일 때, 시각 $t=a$에서 $t=b$까지 점 P가 움직인 거리 s는 다음과 같다.

$s=\int _{a}^{b}{\sqrt {{\biggl (}{dx \over dt}{\biggr )}^{2}+{\biggl (}{dy \over dt}{\biggr )}^{2}}}dt=\int _{a}^{b}{\sqrt {\{f'(t)\}^{2}+\{g'(t)\}^{2}}}dt$

곡선 $x=f(t)$, $y=g(t)$ $(a\leq t\leq b)$의 겹치는 부분이 없을 때 길이 $l$은 다음과 같다.

$l=\int _{a}^{b}{\sqrt {{\biggl (}{dx \over dt}{\biggr )}^{2}+{\biggl (}{dy \over dt}{\biggr )}^{2}}}dt=\int _{a}^{b}{\sqrt {\{f'(t)\}^{2}+\{g'(t)\}^{2}}}dt$

곡선 $y=f(x)$ $(a\leq x\leq b)$의 길이 $l$은 다음과 같다.

$l=\int _{a}^{b}{\sqrt {1+\{f'(t)\}^{2}}}dt$

급수

 이 부분의 본문은 급수입니다.

급수(級數)란 수학에서 수열들의 각 항의 합을 의미한다. 즉, 급수란 여러 수들의 합연산으로 표현된다. 급수의 예로는 아래와 같은 등차수열의 합이 있다. 1 + 2 + 3 + 4 + 5 + ... + 99 + 100 급수에 더해지는 각 항들이 어떤 공식이나 알고리즘에 의해 표현되는 경우도 있다. 난수들로 이루어진 급수도 생각할 수 있다. 급수는 유한 급수와 무한급수로 나눌 수 있다. 유한 급수의 경우 기초적인 대수학의 법칙들만 사용하여도 그 값을 구할 수 있다. 하지만 무한급수는 그 정확한 합을 구하기 위해서는 해석학의 여러 정리들이 필요하다. 예를 들어 등차수열들의 합으로 이루어진 급수의 경우, 다음과 같이 나타낼 수 있다.$$\sum _{n=0}^{k}\,(an+b);$$

등비수열의 합으로 이루어진 급수의 경우, 다음과 같이 나타낼 수 있다.$$\sum _{n=0}^{k}a^{n}.$$

무한급수

$$S_{n}=a_{0}+a_{1}+a_{2}+\cdots +a_{n},$$

무한급수는 위의 $S_{n}$, 즉 급수의 부분합으로 이루어지는 수열의 극한값으로 생각한다. $n$이 무한대로 갈 때, 그 극한이 유한한 값을 갖는다면 이 급수가 수렴한다고 한다. 만약 이 값이 무한하거나 존재하지 않는다면, 이 급수는 발산한다고 한다.

무한급수의 수렴을 판정하는데는 비교판정법, 적분판정법, 일반항판정법, 멱근판정법, 비율판정법 등이 있다.

멱급수

주어진 수열 $\{a\}=(a_{0},\ a_{1},\ a_{2},\ \cdots )$와 변수 $x$에 대해서 $a(x)=a_{0}+a_{1}x+a_{2}x^{2}+\cdots$
를 수열 a로부터 얻은 멱급수라고 부른다.
$\rho \equiv \lim _{n\to \infty }\ \left\vert {\frac {a_{n+1}}{a_{n}}}\right\vert$가 존재한다고 하자.

이때, 이 수열의 멱급수는 $\ |\,x\,|<{\frac {1}{\rho }}$일 때 수렴한다.

테일러 급수

 이 부분의 본문은 테일러 급수입니다.

원점 $0$을 포함하는 구간I에 대해서 정의된 n번 미분가능한 함수 f:I→R 에 대하여
$T_{n}f(x)\equiv \sum _{k=0}^{n}{\frac {f^{(k)}(0)x^{k}}{k!}}$
$f$의 $n$차 근사 다항식이라하고,
$R_{n}f(x)\equiv f(x)-T_{n}f(x)$
를 $n$차 테일러 나머지 항이라고 하자.
그리고 원점 근방에서 정의된 무한번 미분 가능한 함수 $f(x)$에 대하여 멱급수
$Tf(x)\equiv \sum _{n=0}^{\infty }{\frac {f^{(n)}(0)x^{n}}{n!}}$
를 $f$의 테일러 급수라고 한다. 테일러 급수가 원래 함수에 수렴할 필요충분조건은
$\lim _{n\to \infty }R_{n}f(x)=0$ 이다.

교육

세계의 여러 나라에서 미적분학을 가르치고 있다.

대한민국

 이 부분의 본문은 대한민국의 고등학교 수학 교과목입니다.

대한민국에서는 고등학교의 "수학 II" 과목과 "미적분" 과목에서 미적분학을 배운다.

같이 보기

• 푸리에 급수