미적분학의 기본 정리 (微積分學의基本定理, 영어 : fundamental theorem of calculus )는 미분 과 적분 을 서로 연관시키는 정리이다. 미적분학의 기본 정리와 그 증명은 제임스 그레고리(1638–1675)가 발표하였으며, 아이작 베로우(1630–1677)는 더욱 일반적인 경우를 증명하였다. 이후 아이작 베로우의 제자인 아이작 뉴턴이 미적분학의 기본 정리를 완성시켰고, 이 정리의 제안과 증명으로부터 적분과 미분이 통합된 미적분학 이 창시되었다. 독일의 라이프니츠 역시 뉴턴과는 독자적으로 미적분학의 기본 정리의 최종형태를 발견했고, dx와 dy와 같은 무한소를 나타내는 기호를 도입함으로써 미적분학의 발전에 크게 기여하였다.
미적분학의 기본 정리는 두 결과로 구성되며, 이 둘 가운데 하나를 뜻하기도 한다. 미적분학의 제1 기본 정리 는 미분과 적분이 서로 역연산 관계에 있다는 정리이다. 이 정리는 관련이 없어 보이는 두 수학이 아주 긴밀한 관계를 가지고 있음을 보여준다. 미적분학의 제2 기본 정리 는 정적분 을 부정적분 의 차로 간단히 계산할 수 있음을 의미한다. 이 정리가 있기에 계산이 힘든 리만 합 의 극한을 매번 계산할 필요 없이 간단히 부정적분을 사용해 정적분의 값을 계산할 수 있다.
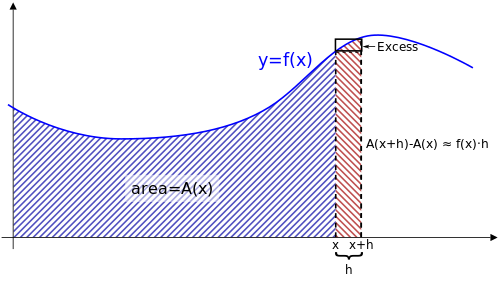
기하학적 직관 [ 편집 ] 빨간색 영역의 넓이는 정확히
A
(
x
+
h
)
−
A
(
x
)
{\displaystyle A(x+h)-A(x)}
h
{\displaystyle h}
f
(
x
)
h
{\displaystyle f(x)h}
연속 함수
f
:
R
→
R
{\displaystyle f\colon \mathbb {R} \to \mathbb {R} }
(
t
,
y
)
{\displaystyle (t,y)}
데카르트 좌표계 를 추가한 평면 위의 곡선으로 나타낼 수 있다. 만약 항상
f
(
t
)
≥
0
{\displaystyle f(t)\geq 0}
t
=
x
{\displaystyle t=x}
A
(
x
)
{\displaystyle A(x)}
리만 적분
A
(
x
)
=
∫
0
x
f
(
t
)
d
t
{\displaystyle A(x)=\int _{0}^{x}f(t)\,dt}
으로 주어진다. 작은 실수
h
>
0
{\displaystyle h>0}
A
(
x
+
h
)
−
A
(
x
)
{\displaystyle A(x+h)-A(x)}
t
=
x
{\displaystyle t=x}
t
=
x
+
h
{\displaystyle t=x+h}
A
(
x
+
h
)
−
A
(
x
)
≈
f
(
x
)
h
{\displaystyle A(x+h)-A(x)\approx f(x)h}
로 근사할 수 있다. 따라서,
h
{\displaystyle h}
A
(
x
+
h
)
−
A
(
x
)
h
≈
f
(
x
)
{\displaystyle {\frac {A(x+h)-A(x)}{h}}\approx f(x)}
이다. 이 근사는 절댓값 이 작은
h
<
0
{\displaystyle h<0}
t
=
x
{\displaystyle t=x}
t
=
x
+
h
{\displaystyle t=x+h}
기울기 이며,
A
{\displaystyle A}
x
{\displaystyle x}
미분
A
′
(
x
)
{\displaystyle A'(x)}
극한
A
′
(
x
)
=
lim
h
→
0
A
(
x
+
h
)
−
A
(
x
)
h
{\displaystyle A'(x)=\lim _{h\to 0}{\frac {A(x+h)-A(x)}{h}}}
으로 주어진다. 따라서,
A
′
(
x
)
=
f
(
x
)
{\displaystyle A'(x)=f(x)}
이다.
물론 직관적인 관찰에는 직사각형 넓이와 실제 넓이의 오차에 대한 고려가 빠져 있다. 사실,
f
{\displaystyle f}
연속 함수 이므로,
h
{\displaystyle h}
t
∈
[
x
,
x
+
h
]
{\displaystyle t\in [x,x+h]}
f
(
t
)
{\displaystyle f(t)}
f
(
t
)
{\displaystyle f(t)}
t
∈
[
x
,
x
+
h
]
{\displaystyle t\in [x,x+h]}
m
{\displaystyle m}
M
{\displaystyle M}
m
h
≤
A
(
x
+
h
)
−
A
(
x
)
≤
M
h
{\displaystyle mh\leq A(x+h)-A(x)\leq Mh}
m
h
≤
f
(
x
)
h
≤
M
h
{\displaystyle mh\leq f(x)h\leq Mh}
에 속한다. 따라서, 기울기와 그 근삿값
f
(
x
)
{\displaystyle f(x)}
M
−
m
{\displaystyle M-m}
|
A
(
x
+
h
)
−
A
(
x
)
h
−
f
(
x
)
|
≤
M
−
m
{\displaystyle \left|{\frac {A(x+h)-A(x)}{h}}-f(x)\right|\leq M-m}
h
{\displaystyle h}
f
{\displaystyle f}
M
−
m
{\displaystyle M-m}
속도와 변위 [ 편집 ] 어떤 물체가 직선 위에서 시간
t
∈
[
t
0
,
t
1
]
{\displaystyle t\in [t_{0},t_{1}]}
속도
v
(
t
)
≥
0
{\displaystyle v(t)\geq 0}
변위
Δ
s
{\displaystyle \Delta s}
연속 함수 ), 시간
t
∈
[
t
0
,
t
1
]
{\displaystyle t\in [t_{0},t_{1}]}
리만 적분
Δ
s
=
∫
t
0
t
1
v
(
t
)
d
t
{\displaystyle \Delta s=\int _{t_{0}}^{t_{1}}v(t)\,dt}
과 같다. 또한,
t
0
{\displaystyle t_{0}}
t
1
{\displaystyle t_{1}}
Δ
s
=
s
(
t
1
)
−
s
(
t
0
)
{\displaystyle \Delta s=s(t_{1})-s(t_{0})}
와 같다. 따라서, 다음이 성립한다.
∫
t
0
t
1
v
(
t
)
d
t
=
s
(
t
1
)
−
s
(
t
0
)
{\displaystyle \int _{t_{0}}^{t_{1}}v(t)\,dt=s(t_{1})-s(t_{0})}
즉, 상수를 더하는 차이를 무시하면, 변위는 속도의 적분과 같다. 다른 한편, 속도는 정의에 따라 변위의 미분 이다.
v
(
t
)
=
s
′
(
t
)
=
lim
Δ
t
→
0
s
(
t
+
Δ
t
)
−
s
(
t
)
Δ
t
{\displaystyle v(t)=s'(t)=\lim _{\Delta t\to 0}{\frac {s(t+\Delta t)-s(t)}{\Delta t}}}
미적분학의 기본 정리 제1 기본 정리 [ 편집 ] 리만 적분 가능 함수
f
:
[
a
,
b
]
→
R
{\displaystyle f\colon [a,b]\to \mathbb {R} }
F
:
[
a
,
b
]
→
R
{\displaystyle F\colon [a,b]\to \mathbb {R} }
F
(
x
)
=
∫
a
x
f
(
t
)
d
t
(
∀
x
∈
[
a
,
b
]
)
{\displaystyle F(x)=\int _{a}^{x}f(t)\,dt\qquad (\forall x\in [a,b])}
미적분학의 제1 기본 정리 에 따르면, 다음이 성립한다.
F
{\displaystyle F}
립시츠 연속 함수 이다. 따라서,
F
{\displaystyle F}
균등 연속 함수 이며, 연속 함수 이다.만약
f
{\displaystyle f}
연속 함수 라면,
F
{\displaystyle F}
미분 가능 함수 이며, 그 미분은
F
′
=
f
{\displaystyle F'=f}
함수
f
{\displaystyle f}
유계 함수 이다. 즉,
M
=
sup
t
∈
[
a
,
b
]
|
f
(
t
)
|
<
∞
{\displaystyle M=\sup _{t\in [a,b]}|f(t)|<\infty }
이다. 따라서, 임의의
a
≤
x
≤
y
≤
b
{\displaystyle a\leq x\leq y\leq b}
|
F
(
y
)
−
F
(
x
)
|
=
|
∫
a
y
f
(
t
)
d
t
−
∫
a
x
f
(
t
)
d
t
|
=
|
∫
x
y
f
(
t
)
d
t
|
≤
∫
x
y
|
f
(
t
)
|
d
t
≤
M
(
y
−
x
)
{\displaystyle |F(y)-F(x)|=\left|\int _{a}^{y}f(t)\,dt-\int _{a}^{x}f(t)\,dt\right|=\left|\int _{x}^{y}f(t)\,dt\right|\leq \int _{x}^{y}|f(t)|\,dt\leq M(y-x)}
이다. 즉,
F
{\displaystyle F}
립시츠 연속 함수 이다.
이제,
f
{\displaystyle f}
연속 함수 라고 가정하고, 임의의
x
∈
[
a
,
b
]
{\displaystyle x\in [a,b]}
ϵ
>
0
{\displaystyle \epsilon >0}
f
{\displaystyle f}
|
f
(
t
)
−
f
(
x
)
|
<
ϵ
(
∀
t
∈
(
x
−
δ
,
x
+
δ
)
∩
[
a
,
b
]
)
{\displaystyle |f(t)-f(x)|<\epsilon \qquad (\forall t\in (x-\delta ,x+\delta )\cap [a,b])}
인
δ
>
0
{\displaystyle \delta >0}
y
∈
(
(
x
−
δ
,
x
)
∪
(
x
+
δ
)
)
∩
[
a
,
b
]
{\displaystyle y\in ((x-\delta ,x)\cup (x+\delta ))\cap [a,b]}
|
F
(
y
)
−
F
(
x
)
y
−
x
−
f
(
x
)
|
=
|
1
y
−
x
∫
x
y
f
(
t
)
d
t
−
1
y
−
x
∫
x
y
f
(
x
)
d
t
|
=
|
1
y
−
x
∫
x
y
(
f
(
t
)
−
f
(
x
)
)
d
t
|
<
ϵ
{\displaystyle \left|{\frac {F(y)-F(x)}{y-x}}-f(x)\right|=\left|{\frac {1}{y-x}}\int _{x}^{y}f(t)\,dt-{\frac {1}{y-x}}\int _{x}^{y}f(x)\,dt\right|=\left|{\frac {1}{y-x}}\int _{x}^{y}(f(t)-f(x))\,dt\right|<\epsilon }
이다. 따라서,
F
{\displaystyle F}
x
{\displaystyle x}
F
′
(
x
)
=
f
(
x
)
{\displaystyle F'(x)=f(x)}
제2 기본 정리 [ 편집 ] 리만 적분 가능 함수
f
:
[
a
,
b
]
→
R
{\displaystyle f\colon [a,b]\to \mathbb {R} }
F
′
=
f
{\displaystyle F'=f}
미분 가능 함수
F
:
[
a
,
b
]
→
R
{\displaystyle F\colon [a,b]\to \mathbb {R} }
F
{\displaystyle F}
f
{\displaystyle f}
부정적분 이다). 미적분학의 제2 기본 정리 에 따르면, 다음 등식이 성립한다.
∫
a
b
f
(
t
)
d
t
=
F
(
b
)
−
F
(
a
)
{\displaystyle \int _{a}^{b}f(t)\,dt=F(b)-F(a)}
폐구간
[
a
,
b
]
{\displaystyle [a,b]}
P
=
(
x
0
P
,
x
1
P
,
…
,
x
n
(
P
)
P
)
{\displaystyle P=(x_{0}^{P},x_{1}^{P},\dots ,x_{n(P)}^{P})}
a
=
x
0
P
<
x
1
P
<
⋯
<
x
n
(
P
)
P
=
b
{\displaystyle a=x_{0}^{P}<x_{1}^{P}<\cdots <x_{n(P)}^{P}=b}
을 생각하자. 평균값 정리 에 따라, 각
i
=
1
,
…
,
n
(
P
)
{\displaystyle i=1,\dots ,n(P)}
F
(
x
i
P
)
−
F
(
x
i
−
1
P
)
=
f
(
ξ
i
P
)
(
x
i
P
−
x
i
−
1
P
)
{\displaystyle F(x_{i}^{P})-F(x_{i-1}^{P})=f(\xi _{i}^{P})(x_{i}^{P}-x_{i-1}^{P})}
인
ξ
i
P
∈
(
x
i
−
1
P
,
x
i
P
)
{\displaystyle \xi _{i}^{P}\in (x_{i-1}^{P},x_{i}^{P})}
i
{\displaystyle i}
F
(
b
)
−
F
(
a
)
=
∑
i
=
1
n
(
P
)
f
(
ξ
i
P
)
(
x
i
P
−
x
i
−
1
P
)
{\displaystyle F(b)-F(a)=\sum _{i=1}^{n(P)}f(\xi _{i}^{P})(x_{i}^{P}-x_{i-1}^{P})}
을 얻는다. 우변은
f
{\displaystyle f}
P
{\displaystyle P}
리만 합 이므로, 분할
P
{\displaystyle P}
리만 적분
F
(
b
)
−
F
(
a
)
=
∫
a
b
f
(
t
)
d
t
{\displaystyle F(b)-F(a)=\int _{a}^{b}f(t)\,dt}
을 얻는다.
일반화 [ 편집 ] 르베그 적분 [ 편집 ] 르베그 적분 은 리만 적분 을 효과적으로 일반화한다. 구체적으로, 모든 리만 적분 가능 함수는 르베그 적분 을 가지며, 이는 리만 적분 과 일치한다. 미적분학의 기본 정리의 르베그 적분 형태가 존재하며, 다음과 같다. 르베그 적분 을 갖는 가측 함수
f
:
[
a
,
b
]
→
R
{\displaystyle f\colon [a,b]\to \mathbb {R} }
F
:
[
a
,
b
]
→
R
{\displaystyle F\colon [a,b]\to \mathbb {R} }
F
(
x
)
=
∫
a
x
f
(
t
)
d
t
(
∀
x
∈
[
a
,
b
]
)
{\displaystyle F(x)=\int _{a}^{x}f(t)\,dt\qquad (\forall x\in [a,b])}
는 절대 연속 함수 이며, 거의 모든
x
∈
[
a
,
b
]
{\displaystyle x\in [a,b]}
F
′
(
x
)
=
f
(
x
)
{\displaystyle F'(x)=f(x)}
미분 가능 함수
F
:
[
a
,
b
]
→
R
{\displaystyle F\colon [a,b]\to \mathbb {R} }
도함수
F
′
=
f
{\displaystyle F'=f}
르베그 적분 을 갖는다면,
∫
a
b
f
(
t
)
d
t
=
F
(
b
)
−
F
(
a
)
{\displaystyle \int _{a}^{b}f(t)\,dt=F(b)-F(a)}
이다.
스토크스 정리 [ 편집 ] 미적분학의 기본 정리는 폐구간 및 0-형식 에 대한 스토크스 정리 와 같다.
같이 보기 [ 편집 ] 참고 문헌 [ 편집 ] 외부 링크 [ 편집 ]






















![{\displaystyle t\in [x,x+h]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b7755cf92fd927bba783907054f6ac416970739)








![{\displaystyle t\in [t_{0},t_{1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b698b33a7f49fc270026c5ecaaad66a0e9e588a)








![{\displaystyle f\colon [a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5ab61178bf5349838758ffe3d96135406ed0245)
![{\displaystyle F\colon [a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/22aae183016ffbb759663208b693d6a28be4e69e)
![{\displaystyle F(x)=\int _{a}^{x}f(t)\,dt\qquad (\forall x\in [a,b])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/638b5668d7153ce65d559ec56afa1701cefdbb8f)


![{\displaystyle M=\sup _{t\in [a,b]}|f(t)|<\infty }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4052d13c2a58f03b2e82ea921575cd5f4806794)


![{\displaystyle x\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/026357b404ee584c475579fb2302a4e9881b8cce)

![{\displaystyle |f(t)-f(x)|<\epsilon \qquad (\forall t\in (x-\delta ,x+\delta )\cap [a,b])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b557f844066d3b820d88c8b72f07d468792e00a4)

![{\displaystyle y\in ((x-\delta ,x)\cup (x+\delta ))\cap [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1589996f15f1d6c3b0dd5ff1167c28113c08acd5)



![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)








