적분
| 관련 문서 둘러보기 |
| 미적분학 |
|---|

적분(한국 한자: 積分, 영어: integral)은 정의된 함수의 그래프와 그 구간으로 둘러싸인 도형의 넓이를 구하는 것이다. 리만 적분에서 다루는 고전적인 정의에 따르면, 실수의 척도를 사용하는 측도 공간에 나타낼 수 있는 연속인 함수 f(x)에 대하여 그 함수의 정의역의 부분 집합을 이루는 구간 [a, b] 에 대응하는 치역으로 이루어진 곡선의 리만 합의 극한을 구하는 것이다. 이를 정적분(定積分, 영어: definite integral)이라 한다. 구간 [a, b]에 대하여 이면 적분은 곡선의 면적과 동일하다. 그러나, 오른쪽 그림과 같이 구간 가운데 일부가 음수인 치역을 갖는다면 적분 값은 서로 상쇄되어 곡선이 이루는 면적과 다를 수 있다.[1]
이를 수식으로 나타내면, 폐구간에서 연속인 함수 에 대한 정적분은 다음과 같은 수식으로 나타낼 수 있다.[1]
역사
[편집]아르키메데스가 적분의 아이디어를 처음 생각해내었고 앙리 르베그가 적분론을 완성하였다.[2]
고대 그리스 시대 시라쿠사의 수학자 아르키메데스는 도형의 면적이나 부피를 구하는데 오늘날의 적분과 유사한 방법을 사용하였다. 아르키메데스는 구적법을 이용하여 원, 구, 포물선의 일부 등에 대한 면적과 부피를 구하는 증명을 제시하였다.[3] 구적법 문제는 이후 오랫동안 별다른 진전을 보이지 못하였다가 르네상스 시기에 이르러 보나벤투라 카발리에리가 무한의 개념을 도입하면서 진전이 있었다. 1622년 카발리에리는 곡선으로 둘러싸인 도형의 면적을 매우 폭이 좁은 직사각형들의 면적을 합한 것으로 이해할 수 있다는 착상을 내놓았다. 이후 블레즈 파스칼은 지금의 적분 기호를 사용한 것은 아니지만 곡선의 면적은 모든 가로 선분의 합인 의 단위, 즉 n에 대한 비와 같다는 것을 파악하고 있었다.[4]
카발리에리 이후 유럽에서는 도형을 당시의 표현을 빌리자면 불가분량이라고 부르는 아주 작은 양으로 나누어 넓이나 부피를 구하는 방법이 지속적으로 연구되었다. 케플러는 케플러의 행성운동법칙에서 지구의 공전 궤도가 타원을 이루며 같은 시간 동안 지구가 지나가는 황도면의 넓이는 같다고 주장하였다. 그는 타원의 넓이를 계산하기 위해 카빌리에리 이후 알려진 불가분량을 이용하였다. 또한, 케플러는 포도주통의 내측 부피를 구하기 위해 포도주통을 이루는 입체도형을 얇은 막들의 집합으로 파악하여 합산하였다. 이러한 발상은 케플러가 적분의 발견에 매우 근접하였다는 것을 보여준다.[5]:77–79[6]
한편, 데카르트가 제시한 좌표 평면과 해석기하학의 출현은 미적분학이 발전하는 중요한 밑거름이 되었다.[7] 아이작 뉴턴과 고트프리트 빌헬름 라이프니츠는 각자 독자적으로 미적분학을 수립하였으며 적분은 결국 미분의 역산으로 역도함수를 구하는 것과 같다는 점을 발견하였다. 이를 미적분학의 기본정리라고 한다.[8]
19세기에 이르러 베른하르트 리만은 적분에 대해 수학적으로 엄밀한 정의를 내렸다. 1823년 오귀스탱 루이 코시는 모든 연속함수는 적분 가능함을 증명하였고, 리만은 이를 확장하여 연속 함수 f(x)의 적분은 해당 구간에서 리만 합의 극한과 같다는 점을 증명하였다. 이렇게 정의된 적분을 흔히 리만 적분이라 한다.[9]:118–119 리만 적분은 이후 토마스 요아너스 스틸티어스에 의해 보다 간단히 정리되었다.[10]
1902년 앙리 르베그는 연속된 함수의 유계 구간에 대해 내측도와 외측도의 개념을 정립하고 이를 덮개로 파악하여 계측하는 르베그 측도를 이용한 르베그 적분을 발표하였다. 르베그 적분은 n차원의 일반적인 함수에 대해 리만 적분을 확장하여 적용한 것이다. 르베그 적분은 특정 함수에 대해 리만 적분이 존재할 때에는 리만 적분과 일치하지만, 그렇지 않은 경우에도 적분 가능한 함수들을 만들어 낸다.[9]:277
미적분학, 특히 적분은 수학의 역사에서 비교적 최근에 발전한 학문으로 꾸준히 확장되고 있다.[9]
어원
[편집]‘적분(積分)’이란 번역어를 근대에 처음 쓴 문헌은 엘리어스 루미스의 《Analytical Geometry and of the Differential and Integral Calculus》(1835)를 1859년 알렉산더 와일리와 이선란이 번역한 《대미적습급(代微積拾級)》이다. 한편 조지프 니덤은 《중국의 과학과 문명》에서 11세기 중국에서 이미 ‘적분’이라는 번역어를 사용했었다고 주장했다.[11]
개요
[편집]적분은 곡면으로 이루어진 도형의 넓이나 물체의 부피와 같은 것에서 중력의 중심을 구하는 문제에 이르기까지 폭넓게 사용된다. 예를 들어 곡면으로 이루어진 수영장을 채우기 위해 얼마만큼의 물이 필요한지를 계산할 수 있다.
임의의 함수 의 정의역 가운데 일부 구간 에 대한 적분은 구간 내의 치역이 모두 이상일 때 해당 구간의 넓이와 같다. 치역의 일부 구간이 음수일 경우 이상인 구간과 상계되어 엄밀한 의미에서 적분과 구간의 넓이는 동일한 개념은 아니지만, 적분의 개요를 이해하기 위해 여기서는 넓이를 구하는 방법으로서 적분을 다룬다.

인 곡선에서 부터 사이의 넓이를 구하는 경우를 가정할 때, 라면. 이것은 다음과 같은 적분식으로 표현할 수 있다.
이제 다음과 같은 방법에 따라 위 식이 나타내는 넓이를 구할 수 있다. 우선 , 이므로 구간 에서 전체의 넓이는 가로와 세로가 각각 1인, 즉 넓이가 1인 정사각형 안에 있다고 할 수 있다. 물론, 여기서 구하고자 하는 곡선의 넓이는 이 전체 구간의 넓이보다 작다. 더욱 정확한 넓이를 계산하기 위해서는 구간을 더 세밀하게 나눌 필요가 있다. 오른쪽 그림의 노란색 사각형과 같이 구간 [0, 1]을 폭이 0.2인 구간으로 나누어 오른쪽 값을 높이로 하는 다섯 개의 사각형을 그릴 수 있다. 이들 사각형의 넓이의 합은
이 된다. 그래프에서 나타난 것과 같이 이 사각형들의 넓이의 합은 실제 넓이보다 여전히 크다.
한편, 오른쪽 그래프의 녹색 사각형은 구간 [0,1]을 12등분하여 왼쪽 값을 높이로 하는 사각형을 그린 것이다. 이 사각형들의 넓이의 합은
이다. 이 경우에는 사각형들의 넓이의 합은 실제 곡선의 넓이보다 작다.
이렇게 작게 나눈 구간의 오른쪽을 사각형의 높이로 삼으면 실제 곡선의 넓이보다 크게 되고 왼쪽을 사각형의 높이로 삼으면 실제 곡선의 넓이보다 작게된다. 그러나, 작게 나눈 구간의 폭을 매우 작게 만들면 둘의 차이는 거의 없게 되고 곡선의 실제 넓이에 근사하게 된다.
이와 같이 적분은 곡선의 넓이를 구하기 위해 밑변의 길이가 0으로 수렴하는 무수히 많은 사각형들의 넓이를 합한 것과 같다. 다항식을 관계식으로 하는 함수의 적분 계산법에 따라 구간 [0,1]에서 의 적분은 다음과 같이 계산된다.
- 단,
계산의 자세한 방법은 이 글의 #표기와 계산 문단에 있다.
지금까지의 예제는 리만 적분에 따른 것이다. 리만 적분에서 함수 f(x)의 적분은 다음과 같이 표기한다.
이때 ∫는 S를 변형시킨 것으로 합한다(영어: summation)는 것을 나타내는 적분 기호이고 는 함수를 는 의 구간에 대한 변화량(영어: differentials)을 곱한다는 의미를 지닌다.
르베그 적분에서는
와 같은 표기를 사용하는데, 리만 적분과는 달리 곡선을 가로로 잘라낸 사각형들의 넓이의 합을 구한다는 의미를 나타낸다.
이 외에도 스토크스의 정리에서는 적분을 보다 일반적으로 정의하여 다음과 같이 표기한다.
표기와 계산
[편집]오늘날 일반적으로 사용되는 적분을 나타내는 표기 은 라이프니츠가 제안한 것이다.[8]:140–141 적분 가능한 함수 f(x)가 있을 때 적분의 표기는 다음과 같다.[12]
- (구간 에 대한 함수 의 적분)
미적분학의 기본정리에 따라 적분은 미분의 역연산이다. 즉, 함수 를 도함수로 하는 원시함수 가 존재한다. 원시함수를 구하는 과정을 부정적분(不定積分)이라 한다. 이를 식으로 나타내면 다음과 같은 관계가 성립한다.[13]
예를 들어, 라고 하면 원시함수 는 다음과 같이 생각하여 구할 수 있다.
이 때 도함수가 인 원시 함수 는 일반적인 다항식을 관계식으로 하는 함수이므로
의 형태가 됨을 알 수 있다. 따라서, 다항식의 도함수 계산법을 이용하면 가 되고, 는 임의의 상수가 된다. 즉,
위 식에서 나타나는 임의의 상수 를 적분상수라고 한다. 원시함수 에 나타나는 적분 상수는 함수 로 미분될 때 이 되어 소멸한다.[14]
일반적으로,
- (단, )
의 꼴을 갖는 다항식을 관계식으로 하는 함수의 원시 함수 F(x)는 다음과 같은 형태가 된다.[15]:246–247
- (C는 적분 상수)
일반적인 경우를 살펴보자. 구간 [a, b]에서 적분 가능한 함수 의 임의의 두 부정적분을 , 라 하자. 라 하자. 구간 에 속하는 임의의 에 대하여, 함수 에 평균값의 정리를 적용하면
를 만족하는 c가 구간 (a, x)에 존재한다. 그런데
이므로
이다. 즉 H(x) = H(a)이다. 구간 (a, b]에 속하는 임의의 x를 택하였으므로, 구간 [a, b]에서 이 식이 성립한다. 즉, 구간 [a, b]에서 H(x)는 상수함수이다. 따라서 H(x) = k (k는 상수)라 할 수 있으므로
이다. 즉, 구간 [a, b]에서 두 함수 F(x)와 G(x)는 상수만큼 차이난다. 따라서 함수 f(x)의 임의의 부정적분 F(x)와 G(x)는 상수만큼 차이난다. 어떤 함수의 부정적분을 적분상수를 이용하여 표기하는 것이 정당함을 알 수 있다.
한편, 함수 f(x)의 구간 [a, b]에 대한 적분은 시작점과 끝점이 있는 유계의 변화량을 뜻하며 이를 정적분(定積分)이라 한다. 구간 [a, b]에 대한 함수 f(x)의 정적분은 다음과 같이 계산될 수 있다. 일반적으로 적분은 정적분을 가리킨다. 또한, 리만 합의 극한으로서 정적분을 정의하는 것을 리만 적분이라고 하며, 별다른 설명이 없을 경우 적분은 흔히 리만 적분을 가리킨다.[16]
(단, 는 의 원시 함수)

위에서 예를 든 의 구간 [4, 9] 에 대한 적분을 계산하면,
구간 [4, 9]에 대한 함수 f(x)=x의 치역은 모두 양수 이므로 위 결과는 구간 [4, 9]에 대한 f(x)=x의 넓이와 같다. 오른쪽의 그래프와 같이 이는 결국 한변의 길이가 9인 직각이등변삼각형의 넓이에서 한변의 길이가 4인 직각이등변삼각형의 넓이를 뺀 것과 동일하고, 그 결과 역시 같다.
위의 예와 같이 적분은 하나의 수로서 와는 무관하다. 즉 다음의 등식이 성립한다.[16]
삼각 함수의 적분
[편집]삼각함수 역시 미분적분의 기본정리를 이용하여 원시 함수를 구한후 정적분을 계산한다. 예를 들어 의 원시 함수는 가 되므로, 구간 [a,b]의 정적분은
와 같이 계산할 수 있다.
적분의 여러 형식
[편집]적분은 여러 가지 형식으로 구분된다. 적분 계산에 대한 정의 방식이 달라 서로 다른 형식으로 분류되는 것이 대부분이지만, 교육적인 목적때문에 구분한 경우도 있다. 가장 일반적으로 널리 쓰이는 적분은 리만 적분과 르베그 적분이다.
리만 적분
[편집]
리만 적분은 주어진 구간에서 리만 합의 극한으로 적분을 정의한다. 폐구간 [a,b]는 다음과 같이 보다 작은 구간으로 분할 될 수 있다.
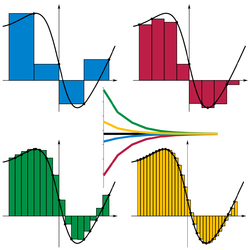
구간 [a,b]를 n 개의 하위 구간으로 분할하는 경우, 하위 구간들은 [xi−1, xi]와 같이 i에 의해 표기될 수 있다. 분할된 각각의 하위 구간의 표시는, ti ∈ [xi−1, xi]와 같이 지정할 수 있다. 함수 f(x)의 특정 구간 [a, b]를 n 개의 하위 구간으로 분할 할 때 리만 합은 다음과 같이 정의된다.
왼쪽의 그래프와 같이 각각의 하위 구간들은 사각형을 구성하게 된다. 이때 곡선과 만나는 어느 지점을 사각형의 높이로 삼을 것인지에 따라 사각형의 크기가 달라지게 된다. 예를 들어 하위 구간의 시작점을 기준으로 한다면 그래프에서는 왼쪽을 기준으로 한 사각형을 그릴 수 있다. 이 경우를 왼쪽 리만 합이라고 한다. 같은 방법으로 하위 구간의 끝점을 기준으로 하는 오른쪽 리만 합, 가운데 지점을 기준으로 하는 가운데 리만 합, 하위 구간에서 곡선의 가장 높은 곳을 기준으로 하는 최댓값 리만 합 등을 만들 수 있다. 왼쪽의 그림에서 가운데에 있는 그래프는 오른쪽 리만 합이든 다른 종류의 리만 합이든 종류에 관계없이 극한을 취할 경우 같은 값으로 수렴함을 보여주고 있다.
구간 [a,b]에 대하여 k를 간격으로 하여 n 개로 분할된 하위 구간의 변량을 Δk = xk−xk−1 라 하면, 전체 구간 [a,b]는 분할 된 각각의 하위 구간들의 합으로 생각할 수 있다. 위에서 설명한 〈적분의 개요〉에서 보았듯이 적분은 하위 구간의 변량 Δk 가 0으로 수렴하는 경우를 구하는 것이다. 즉, 리만 적분은 구간 [a.b]에서 리만 합의 극한을 구하는 것과 같다. 이를 식으로 나타내면 다음과 같다.[17][15]:253–255
르베그 적분
[편집]
르베그 적분은 리만 적분에 비해 보다 광범위하게 적용할 수 있는 적분이다. 예를 들어 리만 적분은 강철 빔의 질량을 쉽게 계산할 수 있지만 강철 구의 경우에는 해결하기가 쉽지 않다. 반면, 르베그 적분은 형태에 제약없이 사용할 수 있다. 르베그 적분은 하중의 계산 등에 흔히 쓰인다.
르베그 적분의 정의는 측도 μ를 정의하는 것에서부터 시작한다. 간단한 경우를 보면, 르베그 측도 μ(A)는 구간 A = [a,b]를 폭으로 삼는다. 이것은 b − a 가 되며, 이 경우 르베그 적분과 리만 적분은 같은 값을 갖는다. 보다 복잡한 경우, 르베그 적분은 불연속 구간에서의 적분과 분할된 구간들이 서로 다른 형상을 갖는 경우 등을 포함한다.
이를 테면 르베그 적분은 리만 적분의 확장이라고 볼 수 있다. 리만 적분이 “함수 f의 구간 [a,b] 에 대하여 분할된 하위 구간의 합”을 살피는 것부터 접근하는데 비해, 르베그 적분은 “함수 f의 범위에 대해 유효한 분할”을 살피는 것에서부터 적분의 정의에 접근한다.[18]
일반적인 접근법은 우선 측도 A의 지시 함수의 적분을 다음과 같이 정의하는 것이다.
- .
측정 가능한 단순 함수 s를 0 이상의 자연수인 n개의 구역으로 분할하면,
이 때, 단순 함수 s에 의한 측도 Ai 에 포함되는 값 ai가 존재한다. 한편, 측정 가능한 E를 다음과 같이 정의한다.
따라서, 함수 f의 르베그 적분은
- ; (s는 단순 함수)
과 같이 되고, 음이 아닌 측정가능한 함수 f의 상한은 다음과 같이 표현할 수 있다.
결국, f의 르베그 적분은
일때
로 정의된다.
기타 적분
[편집]리만 적분과 르베그 적분을 확장한 리만-스틸티어스 적분, 르베그-스틸티어스 적분 등 여러 가지 확장이 존재한다. 적멸적분이라는 방법 역시 있다.
같이 보기
[편집]각주
[편집]- ↑ 가 나 김성수 외, 대학수학, 청문각, 1998년, ISBN 89-7088-171-9, 169-171쪽
- ↑ 변창호, 르베그 적분, 전남대학교 출판부, 2007년, ISBN 89-7598-624-1, 9쪽
- ↑ E.T. 벨, 안재구 역, 수학을 만든 사람들(상), 미래사, ISBN 89-7087-703-7, 13-14쪽, 43-44쪽
- ↑ 변창호, 르베그 적분, 전남대학교 출판부, 2007년, ISBN 89-7598-624-1, 10쪽
- ↑ 마오, 엘리 (2000). 《오일러가 사랑한 수 e》. 번역 허민. 경문사. ISBN 978-89-7282-467-1.
- ↑ 케플러가 적용한 방법은 엄밀하지는 않지만 본질적으로 리만 적분의 방법과 동일한 것이다.
- ↑ E.T. 벨, 안재구 역, 수학을 만든 사람들(상), 미래사, ISBN 89-7087-703-7, 13-14쪽, 48-71쪽
- ↑ 가 나 이광연 (2007). 《수학자들의 전쟁》. 프로네시스. ISBN 89-01-07286-6.
- ↑ 가 나 다 박진홍 (1998). 《미분적분학》. 학문사. ISBN 89-467-4063-9.
- ↑ Thomas Jan Stieltjes
- ↑ Masini, Federico (2005) [1993]. 《근대 중국의 언어와 역사》. 번역 이정재. 소명출판.
- ↑ 하영원, 전기 수학, 기전연구사, 2009년, ISBN 89-336-0807-9, 232쪽
- ↑ 강후경, 이공수학개요, 학문사, 1996, ISBN 89-467-4065-5, 189쪽
- ↑ 한상렬, 현대토목수학, 동화기술, 2010, ISBN 89-425-1522-3, 252-253쪽
- ↑ 가 나 박은순 (2008). 《쉬운 미분·적분학》. 숭실대학교출판부. ISBN 89-7450-235-6.
- ↑ 가 나 김성수, 대학수학, 청문각, 1998년, ISBN 89-7088-171-9, 168-169쪽
- ↑ 김성수, 대학수학, 청문각, 1998년, ISBN 89-7088-171-9, 170쪽
- ↑ Folland, Gerald B. (1984), Real Analysis: Modern Techniques and Their Applications (1st ed.), John Wiley & Sons, ISBN 978-0-471-80958-6
외부 링크
[편집]- “Integral”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4.
- Riemann Sum by Wolfram Research
- Introduction to definite integrals by Khan Academy


![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)













![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)

























![{\displaystyle (a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a6969e731af335df071e247ee7fb331cd1a57ae)








![{\displaystyle [4,9]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e52f81a7e0c9e3e24749e9b3a26c7236a25e302)
















