이중 적분은 그래프 곡면 아래의 부피를 구하는 방법이다. 밑면(직사각형)은 함수의 정의역 을 나타내며, 윗면(쌍곡 포물면 z = 10 - (x 2 - y 2 ) / 8)은 함수의 그래프 를 나타낸다. 미적분학 에서 중적분 (重積分, 영어 : multiple integral )은 정적분 을 다변수 함수 에까지 확장한 것이다.[1] 이중 적분 (二重積分, 영어 : double integral )이라고 하며, 양의 함숫값의 함수의 이중 적분은 함수의 그래프 곡면과
x
y
{\displaystyle xy}
삼중 적분 (三重積分, 영어 : triple integral )이라고 하며, 양의 함숫값의 함수의 삼중 적분 역시 (4차원 공간 속의) 초곡면과 좌표 초평면 사이의 초부피라고 생각할 수 있다. 계산을 위해 2차원에선 극좌표, 3차원에서는 구면좌표계와 원통좌표계를 쓴다.
중적분은 정적분을 여러 번 반복하여 계산할 수 있으며, 이를 푸비니 정리 라고 한다. 복잡한 중적분의 계산에는 변수 변환 을 통해 적분 집합이나 함수를 단순화하는 기법이 필요하며, 이를 치환 적분 이라고 한다.
일변수 함수의 리만 적분 · 리만-스틸티어스 적분 · 르베그 적분 · 르베그-스틸티어스 적분 에 대하여 각각 그에 대응하는 중적분이 존재한다. 임의의 측도 (또는 유한 가법 측도 )에 의한 적분이 주어졌을 때, 이에 대응하는 중적분은 곱측도 에 의한 적분이다.
리만 중적분 [ 편집 ] 조르당 측도 [ 편집 ] 평면 도형이 조르당 가측 집합일 필요 충분 조건은, 각각 안과 밖에 놓인, 직사각형의 유한 합집합을 통해 얻은 근사 넓이가 서로 같다는 것이다. 리만 중적분 (영어 : multiple Riemann integral )의 정의는 조르당 측도 (영어 : Jordan measure/content )에 기반한다.
유계 집합
E
⊆
R
n
{\displaystyle E\subseteq \mathbb {R} ^{n}}
조르당 내측도 (영어 : inner Jordan measure )
m
∗
(
E
)
{\displaystyle \operatorname {m} _{*}(E)}
m
∗
(
E
)
=
sup
{
∑
i
=
1
m
∏
j
=
1
n
(
b
i
j
−
a
i
j
)
:
⨆
i
=
1
m
∏
j
=
1
n
[
a
i
j
,
b
i
j
)
⊆
E
,
a
i
j
,
b
i
j
∈
R
,
m
∈
N
}
{\displaystyle \operatorname {m} _{*}(E)=\sup \left\{\sum _{i=1}^{m}\prod _{j=1}^{n}(b_{ij}-a_{ij})\colon \bigsqcup _{i=1}^{m}\prod _{j=1}^{n}[a_{ij},b_{ij})\subseteq E,\;a_{ij},b_{ij}\in \mathbb {R} ,\;m\in \mathbb {N} \right\}}
비슷하게,
E
{\displaystyle E}
조르당 외측도 (영어 : outer Jordan measure )
m
∗
(
E
)
{\displaystyle \operatorname {m} ^{*}(E)}
m
∗
(
E
)
=
inf
{
∑
i
=
1
m
∏
j
=
1
n
(
b
i
j
−
a
i
j
)
:
⨆
i
=
1
m
∏
j
=
1
n
[
a
i
j
,
b
i
j
)
⊇
E
,
a
i
j
,
b
i
j
∈
R
,
m
∈
N
}
{\displaystyle \operatorname {m} ^{*}(E)=\inf \left\{\sum _{i=1}^{m}\prod _{j=1}^{n}(b_{ij}-a_{ij})\colon \bigsqcup _{i=1}^{m}\prod _{j=1}^{n}[a_{ij},b_{ij})\supseteq E,\;a_{ij},b_{ij}\in \mathbb {R} ,\;m\in \mathbb {N} \right\}}
유계 집합
E
⊆
R
n
{\displaystyle E\subseteq \mathbb {R} ^{n}}
E
{\displaystyle E}
조르당 가측 집합 (영어 : Jordan measurable set )이라고 한다.
m
∗
(
E
)
=
m
∗
(
E
)
=
d
e
f
m
(
E
)
{\displaystyle \operatorname {m} _{*}(E)=\operatorname {m} ^{*}(E)\ {\overset {\underset {\mathrm {def} }{}}{=}}\,\operatorname {m} (E)}
m
(
E
)
{\displaystyle \operatorname {m} (E)}
E
{\displaystyle E}
조르당 측도 라고 한다.
m
∗
(
∂
E
)
=
0
{\displaystyle m^{*}(\partial E)=0}
조르당 측도는 유한 가법 측도 이지만, 이름과 달리 측도 가 아니다. 리만 중적분은 조르당 가측 집합 위에서만 정의된다.
(유계) 조르당 가측 집합
E
⊆
R
n
{\displaystyle E\subseteq \mathbb {R} ^{n}}
분할 (영어 : partition )은 다음 세 조건을 만족시키는 유한 집합족
{
E
i
}
i
=
1
m
⊆
P
(
E
)
{\displaystyle \{E_{i}\}_{i=1}^{m}\subseteq {\mathcal {P}}(E)}
모든
1
≤
i
≤
m
{\displaystyle 1\leq i\leq m}
E
i
{\displaystyle E_{i}}
모든
1
≤
i
<
j
≤
m
{\displaystyle 1\leq i<j\leq m}
m
(
E
i
∩
E
j
)
=
0
{\displaystyle \operatorname {m} (E_{i}\cap E_{j})=0}
E
1
∪
⋯
∪
E
m
=
E
{\displaystyle E_{1}\cup \cdots \cup E_{m}=E}
또한, 분할
{
E
i
}
i
=
1
m
⊆
P
(
E
)
{\displaystyle \{E_{i}\}_{i=1}^{m}\subseteq {\mathcal {P}}(E)}
메시 (영어 : mesh )
λ
(
{
E
i
}
i
=
1
m
)
{\displaystyle \lambda (\{E_{i}\}_{i=1}^{m})}
λ
(
{
E
i
}
i
=
1
m
)
=
max
1
≤
i
≤
m
diam
E
i
{\displaystyle \lambda (\{E_{i}\}_{i=1}^{m})=\max _{1\leq i\leq m}\operatorname {diam} E_{i}}
리만 중적분 [ 편집 ] 함수
f
:
E
→
R
{\displaystyle f\colon E\to \mathbb {R} }
E
⊆
R
n
{\displaystyle E\subseteq \mathbb {R} ^{n}}
{
E
i
}
i
=
1
m
⊆
P
(
E
)
{\displaystyle \{E_{i}\}_{i=1}^{m}\subseteq {\mathcal {P}}(E)}
리만 합 (영어 : Riemann sum )은 다음과 같다.
∑
i
=
1
m
f
(
ξ
1
(
i
)
,
…
,
ξ
n
(
i
)
)
m
(
E
i
)
(
ξ
1
(
i
)
,
…
,
ξ
n
(
i
)
)
∈
E
i
{\displaystyle \sum _{i=1}^{m}f(\xi _{1}^{(i)},\dotsc ,\xi _{n}^{(i)})\operatorname {m} (E_{i})\qquad (\xi _{1}^{(i)},\dotsc ,\xi _{n}^{(i)})\in E_{i}}
또한, 다르부 상합 (영어 : upper Darboux sum )은 다음과 같다.
∑
i
=
1
m
sup
(
x
1
,
…
,
x
n
)
∈
E
i
f
(
x
1
,
…
,
x
n
)
m
(
E
i
)
{\displaystyle \sum _{i=1}^{m}\sup _{(x_{1},\dotsc ,x_{n})\in E_{i}}f(x_{1},\dotsc ,x_{n})\operatorname {m} (E_{i})}
또한, 다르부 하합 (영어 : lower Darboux sum )은 다음과 같다.
∑
i
=
1
m
inf
(
x
1
,
…
,
x
n
)
∈
E
i
f
(
x
1
,
…
,
x
n
)
m
(
E
i
)
{\displaystyle \sum _{i=1}^{m}\inf _{(x_{1},\dotsc ,x_{n})\in E_{i}}f(x_{1},\dotsc ,x_{n})\operatorname {m} (E_{i})}
함수
f
:
E
→
R
{\displaystyle f\colon E\to \mathbb {R} }
E
⊆
R
n
{\displaystyle E\subseteq \mathbb {R} ^{n}}
{
E
i
}
i
=
1
m
{\displaystyle \{E_{i}\}_{i=1}^{m}}
(
ξ
1
(
i
)
,
…
,
ξ
n
(
i
)
)
{\displaystyle (\xi _{1}^{(i)},\dotsc ,\xi _{n}^{(i)})}
f
{\displaystyle f}
E
{\displaystyle E}
리만 적분 가능 함수 (영어 : Riemann integrable function )라고 하며, 이 극한을
f
{\displaystyle f}
리만
n
{\displaystyle n}
(영어 : n-ple Riemann integral )이라고 한다.
∫
E
f
(
x
)
d
x
=
∬
⋯
∫
E
f
(
x
1
,
…
,
x
n
)
d
x
1
⋯
d
x
n
=
lim
λ
(
{
E
i
}
i
=
1
m
)
→
0
∑
i
=
1
m
f
(
ξ
1
(
i
)
,
…
,
ξ
n
(
i
)
)
m
(
E
i
)
{\displaystyle \int _{E}f(x)dx=\iint \cdots \int _{E}f(x_{1},\dotsc ,x_{n})dx_{1}\cdots dx_{n}=\lim _{\lambda (\{E_{i}\}_{i=1}^{m})\to 0}\sum _{i=1}^{m}f(\xi _{1}^{(i)},\dotsc ,\xi _{n}^{(i)})\operatorname {m} (E_{i})}
또한, 다르부 상적분 (영어 : upper Darboux integral )은 다음과 같으며, 이는 항상 존재한다.
∫
E
¯
f
(
x
)
d
x
=
∬
⋯
∫
E
¯
f
(
x
1
,
…
,
x
n
)
d
x
1
⋯
d
x
n
=
lim
λ
(
{
E
i
}
i
=
1
m
)
→
0
∑
i
=
1
m
sup
(
x
1
,
…
,
x
n
)
∈
E
i
f
(
x
1
,
…
,
x
n
)
m
(
E
i
)
=
inf
P
(
E
)
⊇
{
E
i
}
i
=
1
m
∈
dom
λ
∑
i
=
1
m
sup
(
x
1
,
…
,
x
n
)
∈
E
i
f
(
x
1
,
…
,
x
n
)
m
(
E
i
)
{\displaystyle {\begin{aligned}{\overline {\int _{E}}}f(x)dx={\overline {\iint \cdots \int _{E}}}f(x_{1},\dotsc ,x_{n})dx_{1}\cdots dx_{n}&=\lim _{\lambda (\{E_{i}\}_{i=1}^{m})\to 0}\sum _{i=1}^{m}\sup _{(x_{1},\dotsc ,x_{n})\in E_{i}}f(x_{1},\dotsc ,x_{n})\operatorname {m} (E_{i})\\&=\inf _{{\mathcal {P}}(E)\supseteq \{E_{i}\}_{i=1}^{m}\in \operatorname {dom} \lambda }\sum _{i=1}^{m}\sup _{(x_{1},\dotsc ,x_{n})\in E_{i}}f(x_{1},\dotsc ,x_{n})\operatorname {m} (E_{i})\end{aligned}}}
마찬가지로, 다르부 하적분 (영어 : lower Darboux integral )은 다음과 같으며, 이는 항상 존재한다.
∫
E
_
f
(
x
)
d
x
=
∬
⋯
∫
E
_
f
(
x
1
,
…
,
x
n
)
d
x
1
⋯
d
x
n
=
lim
λ
(
{
E
i
}
i
=
1
m
)
→
0
∑
i
=
1
m
inf
(
x
1
,
…
,
x
n
)
∈
E
i
f
(
x
1
,
…
,
x
n
)
m
(
E
i
)
=
sup
P
(
E
)
⊇
{
E
i
}
i
=
1
m
∈
dom
λ
∑
i
=
1
m
inf
(
x
1
,
…
,
x
n
)
∈
E
i
f
(
x
1
,
…
,
x
n
)
m
(
E
i
)
{\displaystyle {\begin{aligned}{\underline {\int _{E}}}f(x)dx={\underline {\iint \cdots \int _{E}}}f(x_{1},\dotsc ,x_{n})dx_{1}\cdots dx_{n}&=\lim _{\lambda (\{E_{i}\}_{i=1}^{m})\to 0}\sum _{i=1}^{m}\inf _{(x_{1},\dotsc ,x_{n})\in E_{i}}f(x_{1},\dotsc ,x_{n})\operatorname {m} (E_{i})\\&=\sup _{{\mathcal {P}}(E)\supseteq \{E_{i}\}_{i=1}^{m}\in \operatorname {dom} \lambda }\sum _{i=1}^{m}\inf _{(x_{1},\dotsc ,x_{n})\in E_{i}}f(x_{1},\dotsc ,x_{n})\operatorname {m} (E_{i})\end{aligned}}}
특히, 리만 이중 적분을
∬
E
f
(
x
,
y
)
d
x
d
y
=
∬
E
f
(
x
,
y
)
d
A
=
lim
λ
(
{
E
i
}
i
=
1
m
)
→
0
∑
i
=
1
m
f
(
ξ
i
,
η
i
)
m
(
E
i
)
{\displaystyle \iint _{E}f(x,y)dxdy=\iint _{E}f(x,y)dA=\lim _{\lambda (\{E_{i}\}_{i=1}^{m})\to 0}\sum _{i=1}^{m}f(\xi _{i},\eta _{i})\operatorname {m} (E_{i})}
와 같이 표기하며, 리만 삼중 적분을
∭
E
f
(
x
,
y
,
z
)
d
x
d
y
d
z
=
∭
E
f
(
x
,
y
,
z
)
d
V
=
lim
λ
(
{
E
i
}
i
=
1
m
)
→
0
∑
i
=
1
m
f
(
ξ
i
,
η
i
,
ζ
i
)
m
(
E
i
)
{\displaystyle \iiint _{E}f(x,y,z)dxdydz=\iiint _{E}f(x,y,z)dV=\lim _{\lambda (\{E_{i}\}_{i=1}^{m})\to 0}\sum _{i=1}^{m}f(\xi _{i},\eta _{i},\zeta _{i})\operatorname {m} (E_{i})}
와 같이 표기한다.
이상 리만 중적분 [ 편집 ] 유계 집합과 (정의역이 조르당 영집합이 아니라면) 유계 함수에 한정된 리만 중적분을 무계 집합과 무계 함수를 허용하는 이상 리만 중적분 (영어 : improper multiple Riemann integral )으로 확장할 수 있다. 일변수 함수에서와 달리, 이상 리만 중적분이 수렴할 필요충분조건은 절대 수렴한다는 것이다.
함수
f
:
E
→
R
{\displaystyle f\colon E\to \mathbb {R} }
E
⊆
R
n
{\displaystyle E\subseteq \mathbb {R} ^{n}}
E
{\displaystyle E}
무계 집합 이다.
f
{\displaystyle f}
유계 함수 이다.임의의
r
>
0
{\displaystyle r>0}
E
∩
B
¯
R
(
0
)
{\displaystyle E\cap {\bar {B}}_{R}(0)}
닫힌집합 이다.
여기서
B
¯
R
(
0
)
=
{
(
x
1
,
…
,
x
n
)
:
x
1
2
+
⋯
x
n
2
≤
R
2
}
{\displaystyle {\bar {B}}_{R}(0)=\{(x_{1},\dotsc ,x_{n})\colon x_{1}^{2}+\cdots x_{n}^{2}\leq R^{2}\}}
닫힌 공 이다.
특히,
E
{\displaystyle E}
E
∩
B
¯
R
(
0
)
{\displaystyle E\cap {\bar {B}}_{R}(0)}
임의의 조르당 가측 닫힌집합
F
⊆
E
{\displaystyle F\subseteq E}
f
{\displaystyle f}
F
{\displaystyle F}
이러한
f
{\displaystyle f}
E
{\displaystyle E}
F
⊆
E
{\displaystyle F\subseteq E}
f
{\displaystyle f}
E
{\displaystyle E}
이상 리만 중적분 이라고 한다.
∬
⋯
∫
E
f
(
x
1
,
…
,
x
n
)
d
x
1
⋯
d
x
n
=
lim
sup
{
r
>
0
:
F
⊇
E
∩
B
¯
R
(
0
)
}
→
∞
∬
⋯
∫
F
f
(
x
1
,
…
,
x
n
)
d
x
1
⋯
d
x
n
{\displaystyle \iint \cdots \int _{E}f(x_{1},\dotsc ,x_{n})dx_{1}\cdots dx_{n}=\lim _{\sup\{r>0\colon F\supseteq E\cap {\bar {B}}_{R}(0)\}\to \infty }\iint \cdots \int _{F}f(x_{1},\dotsc ,x_{n})dx_{1}\cdots dx_{n}}
비슷하게,
E
⊆
R
n
{\displaystyle E\subseteq \mathbb {R} ^{n}}
(
a
1
,
…
,
a
n
)
∈
E
{\displaystyle (a_{1},\dotsc ,a_{n})\in E}
f
:
E
∖
{
(
a
1
,
…
,
a
n
)
}
→
R
{\displaystyle f\colon E\setminus \{(a_{1},\dotsc ,a_{n})\}\to \mathbb {R} }
E
{\displaystyle E}
유계 집합 이다.
f
{\displaystyle f}
무계 함수 이다.임의의
r
>
0
{\displaystyle r>0}
E
∖
B
R
(
a
)
{\displaystyle E\setminus B_{R}(a)}
여기서
B
R
(
a
)
=
{
(
x
1
,
…
,
x
n
)
:
(
x
1
−
a
1
)
2
+
⋯
+
(
x
n
−
a
n
)
2
≤
r
2
}
{\displaystyle B_{R}(a)=\{(x_{1},\dotsc ,x_{n})\colon (x_{1}-a_{1})^{2}+\cdots +(x_{n}-a_{n})^{2}\leq r^{2}\}}
열린 공 이다.
특히,
E
{\displaystyle E}
임의의 조르당 가측 닫힌집합
F
⊆
E
∖
{
(
a
1
,
…
,
a
n
)
}
{\displaystyle F\subseteq E\setminus \{(a_{1},\dotsc ,a_{n})\}}
f
{\displaystyle f}
F
{\displaystyle F}
이러한
f
{\displaystyle f}
E
{\displaystyle E}
F
⊆
E
∖
{
(
a
1
,
…
,
a
n
)
}
{\displaystyle F\subseteq E\setminus \{(a_{1},\dotsc ,a_{n})\}}
f
{\displaystyle f}
E
{\displaystyle E}
이상 리만 중적분 이라고 한다.
∬
⋯
∫
E
f
(
x
1
,
…
,
x
n
)
d
x
1
⋯
d
x
n
=
lim
inf
{
r
>
0
:
F
⊇
E
∖
B
R
(
a
)
}
→
0
+
∬
⋯
∫
F
f
(
x
1
,
…
,
x
n
)
d
x
1
⋯
d
x
n
{\displaystyle \iint \cdots \int _{E}f(x_{1},\dotsc ,x_{n})dx_{1}\cdots dx_{n}=\lim _{\inf\{r>0\colon F\supseteq E\setminus B_{R}(a)\}\to 0^{+}}\iint \cdots \int _{F}f(x_{1},\dotsc ,x_{n})dx_{1}\cdots dx_{n}}
르베그 중적분 [ 편집 ] 르베그 중적분 (영어 : multiple Lebesgue integral )은 유클리드 공간 의 르베그 측도 에 기반하여 정의된다.
리만 적분 가능 함수는 유계 함수 일 필요가 없다. 예를 들어, 정의역이 조르당 영집합인 함수는 항상 리만 적분 가능 함수이다. 그러나, 양의 조르당 측도의 집합들로 임의로 세밀하게 분할될 수 있는 정의역 위의 리만 적분 가능 함수는 항상 유계 함수이다. 특히, 조르당 가측 열린집합 또는 그 폐포 위의 리만 적분 가능 함수는 항상 유계 함수이다.[2]
리만 중적분은 일변수 함수의 리만 적분과 같은 성질들을 갖췄다. 예를 들어, 리만 중적분은 선형성 · 적분 집합에 대한 가법성 · 비엄격 부등식의 보존 · 곱의 적분 가능성 보존 등을 만족시킨다.[2]
누차 적분과의 관계 [ 편집 ] 함수를 먼저 일부 변수에 대하여 적분한 뒤, 다시 남은 변수에 대하여 적분하는 것을 누차 적분 (累次積分, 영어 : repeated integral ) 또는 반복 적분 (反復積分)이라고 한다. 중적분은 일정 조건 아래 누차 적분을 통해 구할 수 있다.
함수
f
:
E
→
R
{\displaystyle f\colon E\to \mathbb {R} }
E
⊆
R
n
{\displaystyle E\subseteq \mathbb {R} ^{n}}
f
{\displaystyle f}
E
{\displaystyle E}
임의의
(
x
1
,
…
,
x
n
)
∈
E
{\displaystyle (x_{1},\dotsc ,x_{n})\in E}
∬
⋯
∫
⏞
{
(
x
m
+
1
,
…
,
x
n
)
:
(
x
1
,
…
,
x
n
)
∈
E
}
n
−
m
f
(
x
1
,
…
,
x
n
)
d
x
m
+
1
⋯
d
x
n
{\displaystyle \overbrace {\iint \cdots \int } _{\{(x_{m+1},\dotsc ,x_{n})\colon (x_{1},\dotsc ,x_{n})\in E\}}^{n-m}f(x_{1},\dotsc ,x_{n})dx_{m+1}\cdots dx_{n}}
그렇다면, 다음이 성립한다.[2]
∬
⋯
∫
⏞
E
n
f
(
x
1
,
…
,
x
n
)
d
x
1
⋯
d
x
n
=
∬
⋯
∫
⏞
{
(
x
1
,
…
,
x
m
)
:
(
x
1
,
…
,
x
n
)
∈
E
}
m
d
x
1
⋯
d
x
m
∬
⋯
∫
⏞
{
(
x
m
+
1
,
…
,
x
n
)
:
(
x
1
,
…
,
x
n
)
∈
E
}
n
−
m
f
(
x
1
,
…
,
x
n
)
d
x
m
+
1
⋯
d
x
n
{\displaystyle \overbrace {\iint \cdots \int } _{E}^{n}f(x_{1},\dotsc ,x_{n})dx_{1}\cdots dx_{n}=\overbrace {\iint \cdots \int } _{\{(x_{1},\dotsc ,x_{m})\colon (x_{1},\dotsc ,x_{n})\in E\}}^{m}dx_{1}\cdots dx_{m}\overbrace {\iint \cdots \int } _{\{(x_{m+1},\dotsc ,x_{n})\colon (x_{1},\dotsc ,x_{n})\in E\}}^{n-m}f(x_{1},\dotsc ,x_{n})dx_{m+1}\cdots dx_{n}}
적분 구역 a ≤ x ≤ b , α (x ) ≤ y ≤ β (x ) 위의 적분은 x 를 고정한 채 y 에 대하여 적분한 뒤, 이를 다시 x 에 대하여 적분한 것과 같다. 일부 특수한 정의역의 경우는 다음과 같다. (여기서
ϕ
≤
ψ
{\displaystyle \phi \leq \psi }
σ
≤
τ
{\displaystyle \sigma \leq \tau }
∬
[
a
,
b
]
×
[
c
,
d
]
f
(
x
,
y
)
d
x
d
y
=
∫
a
b
d
x
∫
c
d
f
(
x
,
y
)
d
y
{\displaystyle \iint _{[a,b]\times [c,d]}f(x,y)dxdy=\int _{a}^{b}dx\int _{c}^{d}f(x,y)dy}
∬
{
(
x
,
y
)
:
a
≤
x
≤
b
,
ϕ
(
x
)
≤
y
≤
ψ
(
x
)
}
f
(
x
,
y
)
d
x
d
y
=
∫
a
b
d
x
∫
ϕ
(
x
)
ψ
(
x
)
f
(
x
,
y
)
d
y
{\displaystyle \iint _{\{(x,y)\colon a\leq x\leq b,\phi (x)\leq y\leq \psi (x)\}}f(x,y)dxdy=\int _{a}^{b}dx\int _{\phi (x)}^{\psi (x)}f(x,y)dy}
∬
{
(
x
,
y
)
:
a
≤
y
≤
b
,
ϕ
(
y
)
≤
x
≤
ψ
(
y
)
}
f
(
x
,
y
)
d
x
d
y
=
∫
a
b
d
y
∫
ϕ
(
y
)
ψ
(
y
)
f
(
x
,
y
)
d
x
{\displaystyle \iint _{\{(x,y)\colon a\leq y\leq b,\phi (y)\leq x\leq \psi (y)\}}f(x,y)dxdy=\int _{a}^{b}dy\int _{\phi (y)}^{\psi (y)}f(x,y)dx}
∭
{
(
x
,
y
,
z
)
:
(
x
,
y
)
∈
Ω
,
ϕ
(
x
,
y
)
≤
z
≤
ψ
(
x
,
y
)
}
f
(
x
,
y
,
z
)
d
x
d
y
d
z
=
∬
Ω
d
x
d
y
∫
ϕ
(
x
,
y
)
ψ
(
x
,
y
)
f
(
x
,
y
,
z
)
d
z
{\displaystyle \iiint _{\{(x,y,z)\colon (x,y)\in \Omega ,\phi (x,y)\leq z\leq \psi (x,y)\}}f(x,y,z)dxdydz=\iint _{\Omega }dxdy\int _{\phi (x,y)}^{\psi (x,y)}f(x,y,z)dz}
∭
{
(
x
,
y
,
z
)
:
(
x
,
z
)
∈
Ω
,
ϕ
(
x
,
z
)
≤
y
≤
ψ
(
x
,
z
)
}
f
(
x
,
y
,
z
)
d
x
d
y
d
z
=
∬
Ω
d
x
d
z
∫
ϕ
(
x
,
z
)
ψ
(
x
,
z
)
f
(
x
,
y
,
z
)
d
y
{\displaystyle \iiint _{\{(x,y,z)\colon (x,z)\in \Omega ,\phi (x,z)\leq y\leq \psi (x,z)\}}f(x,y,z)dxdydz=\iint _{\Omega }dxdz\int _{\phi (x,z)}^{\psi (x,z)}f(x,y,z)dy}
∭
{
(
x
,
y
,
z
)
:
(
y
,
z
)
∈
Ω
,
ϕ
(
y
,
z
)
≤
x
≤
ψ
(
y
,
z
)
}
f
(
x
,
y
,
z
)
d
x
d
y
d
z
=
∬
Ω
d
y
d
z
∫
ϕ
(
y
,
z
)
ψ
(
y
,
z
)
f
(
x
,
y
,
z
)
d
x
{\displaystyle \iiint _{\{(x,y,z)\colon (y,z)\in \Omega ,\phi (y,z)\leq x\leq \psi (y,z)\}}f(x,y,z)dxdydz=\iint _{\Omega }dydz\int _{\phi (y,z)}^{\psi (y,z)}f(x,y,z)dx}
∭
{
(
x
,
y
,
z
)
:
a
≤
x
≤
b
,
(
y
,
z
)
∈
Ω
x
}
f
(
x
,
y
,
z
)
d
x
d
y
d
z
=
∫
a
b
d
x
∬
Ω
x
f
(
x
,
y
,
z
)
d
y
d
z
{\displaystyle \iiint _{\{(x,y,z)\colon a\leq x\leq b,(y,z)\in \Omega _{x}\}}f(x,y,z)dxdydz=\int _{a}^{b}dx\iint _{\Omega _{x}}f(x,y,z)dydz}
∭
{
(
x
,
y
,
z
)
:
a
≤
y
≤
b
,
(
x
,
z
)
∈
Ω
y
}
f
(
x
,
y
,
z
)
d
x
d
y
d
z
=
∫
a
b
d
y
∬
Ω
y
f
(
x
,
y
,
z
)
d
x
d
z
{\displaystyle \iiint _{\{(x,y,z)\colon a\leq y\leq b,(x,z)\in \Omega _{y}\}}f(x,y,z)dxdydz=\int _{a}^{b}dy\iint _{\Omega _{y}}f(x,y,z)dxdz}
∭
{
(
x
,
y
,
z
)
:
a
≤
z
≤
b
,
(
x
,
y
)
∈
Ω
z
}
f
(
x
,
y
,
z
)
d
x
d
y
d
z
=
∫
a
b
d
z
∬
Ω
z
f
(
x
,
y
,
z
)
d
x
d
y
{\displaystyle \iiint _{\{(x,y,z)\colon a\leq z\leq b,(x,y)\in \Omega _{z}\}}f(x,y,z)dxdydz=\int _{a}^{b}dz\iint _{\Omega _{z}}f(x,y,z)dxdy}
∭
{
(
x
,
y
,
z
)
:
a
≤
x
≤
b
,
ϕ
(
x
)
≤
y
≤
ψ
(
x
)
,
σ
(
x
,
y
)
≤
z
≤
τ
(
x
,
y
)
}
f
(
x
,
y
,
z
)
d
x
d
y
d
z
=
∫
a
b
d
x
∫
ϕ
(
x
)
ψ
(
x
)
d
y
∫
σ
(
x
,
y
)
τ
(
x
,
y
)
f
(
x
,
y
,
z
)
d
z
{\displaystyle \iiint _{\{(x,y,z)\colon a\leq x\leq b,\phi (x)\leq y\leq \psi (x),\sigma (x,y)\leq z\leq \tau (x,y)\}}f(x,y,z)dxdydz=\int _{a}^{b}dx\int _{\phi (x)}^{\psi (x)}dy\int _{\sigma (x,y)}^{\tau (x,y)}f(x,y,z)dz}
그러나, 둘째 전제가 없다면 결론이 성립하지 않을 수 있다. 예를 들어, 다음과 같은 함수를 정의하자.
f
(
x
,
y
)
=
{
x
(
x
,
y
)
∈
{
1
,
1
/
2
,
1
/
3
,
…
}
×
Q
0
(
x
,
y
)
∉
{
1
,
1
/
2
,
1
/
3
,
…
}
×
Q
{\displaystyle f(x,y)={\begin{cases}x&(x,y)\in \{1,1/2,1/3,\dots \}\times \mathbb {Q} \\0&(x,y)\not \in \{1,1/2,1/3,\dots \}\times \mathbb {Q} \end{cases}}}
그렇다면,
∬
[
0
,
1
]
×
[
0
,
1
]
f
(
x
,
y
)
d
x
d
y
=
0
{\displaystyle \iint _{[0,1]\times [0,1]}f(x,y)dxdy=0}
∫
0
1
d
y
∫
0
1
f
(
x
,
y
)
d
x
=
0
{\displaystyle \int _{0}^{1}dy\int _{0}^{1}f(x,y)dx=0}
이지만,
f
(
1
/
n
,
y
)
=
1
Q
(
y
)
/
n
{\displaystyle f(1/n,y)=1_{\mathbb {Q} }(y)/n}
n
=
1
,
2
,
…
{\displaystyle n=1,2,\dots }
∫
0
1
d
x
∫
0
1
f
(
x
,
y
)
d
y
{\displaystyle \int _{0}^{1}dx\int _{0}^{1}f(x,y)dy}
는 존재하지 않는다.
치환 적분 [ 편집 ] 극좌표계 원통 좌표계 구면 좌표계 함수
g
:
E
→
R
n
{\displaystyle g\colon E\to \mathbb {R} ^{n}}
E
⊆
R
n
{\displaystyle E\subseteq \mathbb {R} ^{n}}
닫힌집합 ) 및
f
:
g
(
E
)
→
R
{\displaystyle f\colon g(E)\to \mathbb {R} }
g
{\displaystyle g}
단사
C
1
{\displaystyle {\mathcal {C}}^{1}}
임의의
t
∈
D
{\displaystyle t\in D}
det
J
g
(
t
)
≠
0
{\displaystyle \det J_{g}(t)\neq 0}
f
{\displaystyle f}
g
(
E
)
{\displaystyle g(E)}
그렇다면, 다음이 성립한다.
∫
g
(
E
)
f
(
x
)
d
x
=
∫
E
f
(
g
(
t
)
)
|
det
J
g
(
t
)
|
d
t
{\displaystyle \int _{g(E)}f(x)dx=\int _{E}f(g(t))\left|\det J_{g}(t)\right|dt}
여기서
det
J
g
{\displaystyle \det J_{g}}
g
{\displaystyle g}
야코비 행렬식 인데, 어떤 점에서의 야코비 행렬식의 값은 대략 변환이 그 점 주위의 초부피를 확대시키는 배수를 나타낸다.
예를 들어, 극좌표 변환
x
=
r
cos
θ
{\displaystyle x=r\cos \theta }
y
=
r
sin
θ
{\displaystyle y=r\sin \theta }
det
∂
(
x
,
y
)
∂
(
r
,
θ
)
=
|
cos
θ
−
r
sin
θ
sin
θ
r
cos
θ
|
=
r
{\displaystyle \det {\frac {\partial (x,y)}{\partial (r,\theta )}}={\begin{vmatrix}\cos \theta &-r\sin \theta \\\sin \theta &r\cos \theta \end{vmatrix}}=r}
에 의한 치환 적분 공식은 다음과 같다.
∬
D
f
(
x
,
y
)
d
x
d
y
=
∬
g
−
1
(
D
)
f
(
r
cos
θ
,
r
sin
θ
)
r
d
r
d
θ
{\displaystyle \iint _{D}f(x,y)dxdy=\iint _{g^{-1}(D)}f(r\cos \theta ,r\sin \theta )rdrd\theta }
또한, 원통 좌표 변환
x
=
r
cos
θ
{\displaystyle x=r\cos \theta }
y
=
r
sin
θ
{\displaystyle y=r\sin \theta }
z
=
z
{\displaystyle z=z}
det
∂
(
x
,
y
,
z
)
∂
(
r
,
θ
,
z
)
=
r
{\displaystyle \det {\frac {\partial (x,y,z)}{\partial (r,\theta ,z)}}=r}
에 의한 치환 적분 공식은 다음과 같다.
∭
D
f
(
x
,
y
,
z
)
d
x
d
y
d
z
=
∭
g
−
1
(
D
)
f
(
r
cos
θ
,
r
sin
θ
,
z
)
r
d
r
d
θ
{\displaystyle \iiint _{D}f(x,y,z)dxdydz=\iiint _{g^{-1}(D)}f(r\cos \theta ,r\sin \theta ,z)rdrd\theta }
또한, 구면 좌표 변환
x
=
r
cos
θ
sin
φ
{\displaystyle x=r\cos \theta \sin \varphi }
y
=
r
sin
θ
sin
φ
{\displaystyle y=r\sin \theta \sin \varphi }
z
=
r
cos
φ
{\displaystyle z=r\cos \varphi }
det
∂
(
x
,
y
,
z
)
∂
(
r
,
θ
,
φ
)
=
−
r
2
sin
φ
{\displaystyle \det {\frac {\partial (x,y,z)}{\partial (r,\theta ,\varphi )}}=-r^{2}\sin \varphi }
에 의한 치환 적분 공식은 다음과 같다.
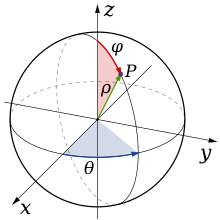
∭
D
f
(
x
,
y
,
z
)
d
x
d
y
d
z
=
∭
g
−
1
(
D
)
f
(
r
cos
θ
sin
φ
,
r
sin
θ
sin
φ
,
r
cos
φ
)
r
2
sin
φ
d
r
d
θ
d
φ
{\displaystyle \iiint _{D}f(x,y,z)dxdydz=\iiint _{g^{-1}(D)}f(r\cos \theta \sin \varphi ,r\sin \theta \sin \varphi ,r\cos \varphi )r^{2}\sin \varphi drd\theta d\varphi }
기하학적 성질 [ 편집 ] 음이 아닌 값의 함수
f
:
E
→
R
{\displaystyle f\colon E\to \mathbb {R} }
E
⊆
R
n
{\displaystyle E\subseteq \mathbb {R} ^{n}}
∬
⋯
∫
E
f
(
x
1
,
…
,
x
n
)
d
x
1
⋯
d
x
n
=
m
(
{
(
x
1
,
…
,
x
n
+
1
)
:
(
x
1
,
…
,
x
n
)
∈
E
,
0
≤
x
n
+
1
≤
f
(
x
1
,
…
,
x
n
)
}
)
{\displaystyle \iint \cdots \int _{E}f(x_{1},\dotsc ,x_{n})dx_{1}\cdots dx_{n}=\operatorname {m} (\{(x_{1},\dotsc ,x_{n+1})\colon (x_{1},\dotsc ,x_{n})\in E,\;0\leq x_{n+1}\leq f(x_{1},\dotsc ,x_{n})\})}
특히, 상수 함수 1의 리만 중적분은 정의역의 조르당 측도와 같다.
∬
⋯
∫
E
d
x
1
⋯
d
x
n
=
m
(
E
)
{\displaystyle \iint \cdots \int _{E}dx_{1}\cdots dx_{n}=\operatorname {m} (E)}
이상 중적분의 성질 [ 편집 ] 이상 중적분 역시 중적분과 비슷한 성질들을 만족시킨다.
예를 들어, 함수
f
:
[
a
,
∞
)
×
[
b
,
∞
)
→
R
{\displaystyle f\colon [a,\infty )\times [b,\infty )\to \mathbb {R} }
임의의 조르당 가측 닫힌집합
F
⊆
[
a
,
∞
)
×
[
b
,
∞
)
{\displaystyle F\subseteq [a,\infty )\times [b,\infty )}
f
{\displaystyle f}
F
{\displaystyle F}
그렇다면, 다음이 성립한다.[3] :175, 定理15.5.4
만약
∫
a
∞
d
x
∫
b
∞
|
f
(
x
,
y
)
|
d
y
<
∞
{\displaystyle \int _{a}^{\infty }dx\int _{b}^{\infty }|f(x,y)|dy<\infty }
∬
[
a
,
∞
)
×
[
b
,
∞
)
f
(
x
,
y
)
d
x
d
y
=
∫
a
∞
d
x
∫
b
∞
|
f
(
x
,
y
)
|
d
y
{\displaystyle \iint _{[a,\infty )\times [b,\infty )}f(x,y)dxdy=\int _{a}^{\infty }dx\int _{b}^{\infty }|f(x,y)|dy}
만약
∫
a
∞
d
x
∫
b
∞
|
f
(
x
,
y
)
|
d
y
=
∞
{\displaystyle \int _{a}^{\infty }dx\int _{b}^{\infty }|f(x,y)|dy=\infty }
∬
[
a
,
∞
)
×
[
b
,
∞
)
f
(
x
,
y
)
d
x
d
y
{\displaystyle \iint _{[a,\infty )\times [b,\infty )}f(x,y)dxdy}
또한, 무계 닫힌집합
E
⊆
R
n
{\displaystyle E\subseteq \mathbb {R} ^{n}}
C
1
{\displaystyle {\mathcal {C}}^{1}}
g
:
E
→
R
n
{\displaystyle g\colon E\to \mathbb {R} ^{n}}
f
:
g
(
E
)
→
R
{\displaystyle f\colon g(E)\to \mathbb {R} }
∬
⋯
∫
g
(
E
)
f
(
x
)
d
x
=
∬
⋯
∫
E
f
(
g
(
t
)
)
|
det
J
g
(
t
)
|
d
t
{\displaystyle \iint \cdots \int _{g(E)}f(x)dx=\iint \cdots \int _{E}f(g(t))\left|\det J_{g}(t)\right|dt}
가운데 하나가 존재한다면, 남은 하나도 존재하며, 이 둘은 서로 같다.[3] :175, 정리 15.5.5
이상 리만 중적분
∬
⋯
∫
E
f
(
x
1
,
…
,
x
n
)
d
x
1
⋯
d
x
n
{\displaystyle \iint \cdots \int _{E}f(x_{1},\dotsc ,x_{n})dx_{1}\cdots dx_{n}}
이 수렴할 필요충분조건은
∬
⋯
∫
E
|
f
(
x
1
,
…
,
x
n
)
|
d
x
1
⋯
d
x
n
<
∞
{\displaystyle \iint \cdots \int _{E}|f(x_{1},\dotsc ,x_{n})|dx_{1}\cdots dx_{n}<\infty }
이다. 즉, 일변수 함수의 경우와 달리, 이상 리만 중적분이 수렴할 필요충분조건은 절대 수렴이다.
직육면체의 부피 [ 편집 ] 직육면체
[
0
,
1
]
×
[
0
,
2
]
×
[
0
,
3
]
{\displaystyle [0,1]\times [0,2]\times [0,3]}
∭
[
0
,
1
]
×
[
0
,
2
]
×
[
0
,
3
]
d
x
d
y
d
z
=
∫
0
1
d
x
∫
0
2
d
y
∫
0
3
d
z
=
∫
0
1
d
x
∫
0
2
3
d
y
=
∫
0
1
6
d
x
=
6
{\displaystyle {\begin{aligned}\iiint _{[0,1]\times [0,2]\times [0,3]}dxdydz&=\int _{0}^{1}dx\int _{0}^{2}dy\int _{0}^{3}dz\\&=\int _{0}^{1}dx\int _{0}^{2}3dy\\&=\int _{0}^{1}6dx\\&=6\end{aligned}}}
삼각뿔의 부피 [ 편집 ] 삼각뿔
{
(
x
,
y
,
z
)
:
0
≤
x
,
y
,
z
≤
x
+
y
+
z
≤
1
}
{\displaystyle \{(x,y,z)\colon 0\leq x,y,z\leq x+y+z\leq 1\}}
∭
{
(
x
,
y
,
z
)
:
0
≤
x
,
y
,
z
≤
x
+
y
+
z
≤
1
}
d
x
d
y
d
z
=
∫
0
1
d
x
∫
0
1
−
x
d
y
∫
0
1
−
x
−
y
d
z
=
∫
0
1
d
x
∫
0
1
−
x
(
1
−
x
−
y
)
d
y
=
∫
0
1
(
1
−
x
)
2
2
d
x
=
1
6
{\displaystyle {\begin{aligned}\iiint _{\{(x,y,z)\colon 0\leq x,y,z\leq x+y+z\leq 1\}}dxdydz&=\int _{0}^{1}dx\int _{0}^{1-x}dy\int _{0}^{1-x-y}dz\\&=\int _{0}^{1}dx\int _{0}^{1-x}(1-x-y)dy\\&=\int _{0}^{1}{\frac {(1-x)^{2}}{2}}dx\\&={\frac {1}{6}}\end{aligned}}}
이차 곡면으로 둘러싸인 도형의 부피 [ 편집 ] 타원 포물면 z = x 2 + y 2 와 원기둥 x 2 + y 2 = a 2 에 의해 둘러싸인 도형구 x 2 + y 2 + z 2 = a 2 와 원뿔 z 2 = (x 2 + y 2 )tana 에 의해 둘러싸인 도형타원 포물면 과 원기둥 으로 둘러싸인 도형
{
(
x
,
y
,
z
)
:
0
≤
z
≤
x
2
+
y
2
≤
a
2
}
{\displaystyle \{(x,y,z)\colon 0\leq z\leq x^{2}+y^{2}\leq a^{2}\}}
∭
{
(
x
,
y
,
z
)
:
0
≤
z
≤
x
2
+
y
2
≤
a
2
}
d
x
d
y
d
z
=
∫
0
a
r
d
r
∫
0
2
π
d
θ
∫
0
r
d
z
=
∫
0
a
r
2
d
r
∫
0
2
π
d
θ
=
∫
0
a
2
π
r
2
d
r
=
2
3
π
a
3
{\displaystyle {\begin{aligned}\iiint _{\{(x,y,z)\colon 0\leq z\leq x^{2}+y^{2}\leq a^{2}\}}dxdydz&=\int _{0}^{a}rdr\int _{0}^{2\pi }d\theta \int _{0}^{r}dz\\&=\int _{0}^{a}r^{2}dr\int _{0}^{2\pi }d\theta \\&=\int _{0}^{a}2\pi r^{2}dr\\&={\frac {2}{3}}\pi a^{3}\end{aligned}}}
구 와 원뿔 로 둘러싸인 도형
{
(
x
,
y
,
z
)
:
x
2
+
y
2
cot
α
≤
z
≤
a
2
−
x
2
−
y
2
}
{\displaystyle \textstyle \left\{(x,y,z)\colon {\sqrt {x^{2}+y^{2}}}\cot \alpha \leq z\leq {\sqrt {a^{2}-x^{2}-y^{2}}}\right\}}
∭
{
(
x
,
y
,
z
)
:
x
2
+
y
2
cot
α
≤
z
≤
a
2
−
x
2
−
y
2
}
d
x
d
y
d
z
=
∫
0
α
sin
φ
d
φ
∫
0
2
π
d
θ
∫
0
a
r
2
d
r
=
1
3
a
3
∫
0
α
sin
φ
d
φ
∫
0
2
π
d
θ
=
2
3
π
a
3
∫
0
α
sin
φ
d
φ
=
2
3
π
a
3
(
1
−
cos
α
)
{\displaystyle {\begin{aligned}\iiint _{\left\{(x,y,z)\colon {\sqrt {x^{2}+y^{2}}}\cot \alpha \leq z\leq {\sqrt {a^{2}-x^{2}-y^{2}}}\right\}}dxdydz&=\int _{0}^{\alpha }\sin \varphi d\varphi \int _{0}^{2\pi }d\theta \int _{0}^{a}r^{2}dr\\&={\frac {1}{3}}a^{3}\int _{0}^{\alpha }\sin \varphi d\varphi \int _{0}^{2\pi }d\theta \\&={\frac {2}{3}}\pi a^{3}\int _{0}^{\alpha }\sin \varphi d\varphi \\&={\frac {2}{3}}\pi a^{3}(1-\cos \alpha )\end{aligned}}}
치환 적분의 예 [ 편집 ] 극좌표 변환 · 원통 좌표 변환 · 구면 좌표 변환 외의 변환을 사용하여 구할 수 있는 중적분의 한 가지 예는 다음과 같다.
∬
{
(
x
,
y
)
:
0
≤
x
,
y
≤
x
+
y
≤
1
}
x
y
x
+
y
d
x
d
y
{\displaystyle \iint _{\{(x,y)\colon 0\leq x,y\leq x+y\leq 1\}}{\sqrt {\frac {xy}{x+y}}}dxdy}
여기에서 다음과 같은 변환을 사용하자.
x
=
r
cos
2
θ
{\displaystyle x=r\cos ^{2}\theta }
y
=
r
sin
2
θ
{\displaystyle y=r\sin ^{2}\theta }
이 변환의 야코비 행렬식 은 다음과 같다.
det
∂
(
x
,
y
)
∂
(
r
,
θ
)
=
|
cos
2
θ
−
r
sin
2
θ
sin
2
θ
r
sin
2
θ
|
=
r
sin
2
θ
{\displaystyle \det {\frac {\partial (x,y)}{\partial (r,\theta )}}={\begin{vmatrix}\cos ^{2}\theta &-r\sin 2\theta \\\sin ^{2}\theta &r\sin 2\theta \end{vmatrix}}=r\sin 2\theta }
따라서 상술 이중 적분을 다음과 같이 구할 수 있다.
∬
{
(
x
,
y
)
:
0
≤
x
,
y
≤
x
+
y
≤
1
}
x
y
x
+
y
d
x
d
y
=
1
2
∫
0
1
r
3
d
r
∫
0
π
2
sin
2
2
θ
d
θ
=
π
20
{\displaystyle \iint _{\{(x,y)\colon 0\leq x,y\leq x+y\leq 1\}}{\sqrt {\frac {xy}{x+y}}}dxdy={\frac {1}{2}}\int _{0}^{1}{\sqrt {r^{3}}}dr\int _{0}^{\frac {\pi }{2}}\sin ^{2}2\theta d\theta ={\frac {\pi }{20}}}
이상 중적분의 예 [ 편집 ] 가우스 함수 의 적분
∫
0
∞
e
−
x
2
d
x
{\displaystyle \int _{0}^{\infty }e^{-x^{2}}dx}
은 이상 중적분
∬
R
2
e
−
x
2
−
y
2
d
x
d
y
{\displaystyle \iint _{\mathbb {R} ^{2}}e^{-x^{2}-y^{2}}dxdy}
을 통해 구할 수 있는데, 이는
∬
R
2
e
−
x
2
−
y
2
d
x
d
y
=
lim
a
→
∞
∬
[
−
a
,
a
]
×
[
−
a
,
a
]
e
−
x
2
−
y
2
d
x
d
y
=
lim
a
→
∞
∫
−
a
a
e
−
x
2
d
x
∫
−
a
a
e
−
y
2
d
y
=
4
(
∫
0
∞
e
−
x
2
d
x
)
2
{\displaystyle {\begin{aligned}\iint _{\mathbb {R} ^{2}}e^{-x^{2}-y^{2}}dxdy&=\lim _{a\to \infty }\iint _{[-a,a]\times [-a,a]}e^{-x^{2}-y^{2}}dxdy\\&=\lim _{a\to \infty }\int _{-a}^{a}e^{-x^{2}}dx\int _{-a}^{a}e^{-y^{2}}dy\\&=4\left(\int _{0}^{\infty }e^{-x^{2}}dx\right)^{2}\end{aligned}}}
이기 때문이다. 이 이상 중적분의 값은
∬
R
2
e
−
x
2
−
y
2
d
x
d
y
=
lim
a
→
∞
∬
{
(
x
,
y
)
:
x
2
+
y
2
≤
a
2
}
e
−
x
2
−
y
2
d
x
d
y
=
lim
a
→
∞
∬
{
(
r
,
θ
)
:
0
≤
r
≤
a
,
0
≤
θ
≤
2
π
}
e
−
r
2
r
d
r
d
θ
=
lim
a
→
∞
∫
0
a
e
−
r
2
r
d
r
∫
0
2
π
d
θ
=
π
{\displaystyle {\begin{aligned}\iint _{\mathbb {R} ^{2}}e^{-x^{2}-y^{2}}dxdy&=\lim _{a\to \infty }\iint _{\{(x,y)\colon x^{2}+y^{2}\leq a^{2}\}}e^{-x^{2}-y^{2}}dxdy\\&=\lim _{a\to \infty }\iint _{\{(r,\theta )\colon 0\leq r\leq a,\;0\leq \theta \leq 2\pi \}}e^{-r^{2}}rdrd\theta \\&=\lim _{a\to \infty }\int _{0}^{a}e^{-r^{2}}rdr\int _{0}^{2\pi }d\theta \\&=\pi \end{aligned}}}
이므로, 가우스 함수의 적분 값은
∫
0
∞
e
−
x
2
d
x
=
π
2
{\displaystyle \int _{0}^{\infty }e^{-x^{2}}dx={\frac {\sqrt {\pi }}{2}}}
이다.
외부 링크 [ 편집 ]
























































![{\displaystyle \iint _{[a,b]\times [c,d]}f(x,y)dxdy=\int _{a}^{b}dx\int _{c}^{d}f(x,y)dy}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1016de94be4c0a651bcb5e1b980341a5271e54c7)










![{\displaystyle \iint _{[0,1]\times [0,1]}f(x,y)dxdy=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/641f45be6eb345752c6cbf3f53faf67bde299056)




































![{\displaystyle [0,1]\times [0,2]\times [0,3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8903de200f226a575b5e2e7633f8c0d2e8e59af0)
![{\displaystyle {\begin{aligned}\iiint _{[0,1]\times [0,2]\times [0,3]}dxdydz&=\int _{0}^{1}dx\int _{0}^{2}dy\int _{0}^{3}dz\\&=\int _{0}^{1}dx\int _{0}^{2}3dy\\&=\int _{0}^{1}6dx\\&=6\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b115bb7dbfd038109e6c9784a79276c153449cf)













![{\displaystyle {\begin{aligned}\iint _{\mathbb {R} ^{2}}e^{-x^{2}-y^{2}}dxdy&=\lim _{a\to \infty }\iint _{[-a,a]\times [-a,a]}e^{-x^{2}-y^{2}}dxdy\\&=\lim _{a\to \infty }\int _{-a}^{a}e^{-x^{2}}dx\int _{-a}^{a}e^{-y^{2}}dy\\&=4\left(\int _{0}^{\infty }e^{-x^{2}}dx\right)^{2}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6a98d7636ad76aa75a78401a14e26719db18381)

