함수의 그래프 와 그 접선 . 함수의 점에서의 미분은 그 점에서의 접선의 기울기 와 같다.미분 (한국 한자 : 영어 : derivative ) 또는 도함수 (한국 한자 : 함수 의 정의역 속 각 점에서 함숫값의 변화량과 독립 변숫값의 변화량 비의 극한 혹은 극한들로 치역이 구성되는 새로운 함수다.[1] 순간 변화율 (미분계수)을 구하는 것을 의미하며 순간변화율은 독립 변수 x의 증분에 관한 함숫값 ƒ(x)의 증분의 비가 한없이 일정한 값에 가까워질 때 그 일정한 값, 즉 함수에서 변수 x값의 변화량에 관한 함숫값 ƒ(x)의 변화량 비가 한없이 일정한 값에 가까워질 때 그 일정한 값 dy/dx 로 나타낸다.
동사로서 미분(영어 : differentiation )은 이러한 극한이나 도함수를 구하는 일, 즉 미분법을 뜻하기도 한다. 도함수에서 미분의 역연산을 통해 원시함수(antiderivative)를 구하는 것 역시 미분법(differential calculus)의 주요 주제다.
미분은 비선형 함수를 선형함수로 근사적으로 나타내려는 시도다. 비선형 함수를 미분하여 한 점 주변에서 1차 함수로 생각한다. 이를 반복하면 함수의 다항함수 근사를 얻으며 무한 번 하면 테일러 급수 를 얻는다. 이는 14세기 인도 수학자의 저작에도 등장한다. 기하학적으로는, 비선형적인 함수로 표현되는 곡선의 한 점에서 그 곡선과 비슷한 직선인 접선을 구하는 것으로도 볼 수 있다. 일반적으로 미분기하학 에서는 선형 공간인 접공간 을 생각하여 미분다양체 를 선형적으로 바라보며, 미분형식 , 미분다양체에서 적분 등은 모두 접공간이 필수적으로 고려되어야 한다.
함수 미분은 존재하지 않을 수 있다. 미분이 모든 곳에서 존재하는 함수를 미분 가능 함수 라고 한다. 미분 가능 함수는 반드시 연속 함수 (=독립 변수의 변화가 미세할 때 함숫값의 변화 역시 미세한 함수)이어야 한다. 그러나 연속 함수가 반드시 미분 가능 함수이지는 않다. 연속함수이지만 모든 정의역에서 미분 불가능한 함수가 아주 많이 존재한다(예: 바이어슈트라스 함수 ). 함수 미분을 정의역 속 각 점에 그 점에서의 미분을 대응시키는 함수 (도함수)로 여길 수 있다. 따라서, 함수의 도함수의 도함수, 함수의 도함수의 도함수의 도함수 따위를 생각할 수 있으며, 이들을 그 함수의 고계 도함수(高階導函數, 영어 : higher order derivative ) 또는 고계 미분(高階微分)이라고 한다. 이런 고계미분이 되고 그 고계도함수가 연속함수인 함수들의 집합을 기호로
C
0
{\displaystyle {\mathcal {C}}^{0}}
C
1
{\displaystyle {\mathcal {C}}^{1}}
C
n
{\displaystyle {\mathcal {C}}^{n}}
C
∞
{\displaystyle {\mathcal {C}}^{\infty }}
C
ω
{\displaystyle {\mathcal {C}}^{\omega }}
미적분학의 기본 정리 에 따르면 원시함수는 부정적분 과 같아서 정적분 을 미분법의 역연산을 통해 구할 수 있으므로 미분과 적분 은 대략 서로 역연산의 관계이다.
미분의 개념에 대한 여러 가지 일반화가 존재한다. 벡터 미적분학 의 기울기 , 다변수 미적분학 의 야코비 행렬 , 함수해석학 의 프레셰 도함수 따위가 있다. 또한, 미분을 주어진 함수에 새 함수를 대응시키는 연산자(미분 연산자 )로 생각할 수 있다.
미분이 나오는 예 [ 편집 ] 접선 문제 [ 편집 ] 곡선의 서로 다른 두 점의 연결선을 할선 이라고 한다. 접선 은 할선의 극한이다.할선은
Δ
x
→
0
{\displaystyle \Delta x\to 0}
기하학 적 관점에서, 미분은 주어진 곡선 의 접선 을 구하는 문제와 동치이다. 접선의 기하학적 의미는 곡선과 스치듯이 만나는 직선이다. 즉, 직선에 미세한 변화를 가하면 곡선과의 교점의 개수가 변화하게 된다. 예를 들어, 직선
x
=
0
{\displaystyle x=0}
y
=
0
{\displaystyle y=0}
포물선
y
=
x
2
{\displaystyle y=x^{2}}
평면 곡선
y
=
f
(
x
)
{\displaystyle y=f(x)}
(
a
,
f
(
a
)
)
{\displaystyle (a,f(a))}
(
x
,
f
(
x
)
)
{\displaystyle (x,f(x))}
x
≠
a
{\displaystyle x\neq a}
k
¯
{\displaystyle {\bar {k}}}
k
¯
=
Δ
y
Δ
x
=
f
(
x
)
−
f
(
a
)
x
−
a
{\displaystyle {\bar {k}}={\frac {\Delta y}{\Delta x}}={\frac {f(x)-f(a)}{x-a}}}
점
(
x
,
f
(
x
)
)
{\displaystyle (x,f(x))}
(
a
,
f
(
a
)
)
{\displaystyle (a,f(a))}
k
=
tan
α
=
lim
Δ
x
→
0
Δ
y
Δ
x
=
lim
x
→
a
f
(
x
)
−
f
(
a
)
x
−
a
{\displaystyle k=\tan \alpha =\lim _{\Delta x\to 0}{\frac {\Delta y}{\Delta x}}=\lim _{x\to a}{\frac {f(x)-f(a)}{x-a}}}
접선의 기울기 역시 함수의 변화량과 독립 변수의 변화량의 비의 극한이므로, 함수의 미분과 같다. 즉,
k
=
tan
α
=
f
′
(
a
)
=
d
y
d
x
|
x
=
a
{\displaystyle k=\tan \alpha =f'(a)=\left.{\frac {dy}{dx}}\right|_{x=a}}
이다.
증분과 평균 변화율과 순간 변화율 [ 편집 ] 일반적인 함수
y
=
f
(
x
)
{\displaystyle y=f(x)}
증분 (增分, 영어 : increment )은 독립 변숫값의 변화량
Δ
x
{\displaystyle \Delta x}
및 함숫값의 변화량
Δ
y
=
f
(
x
+
Δ
x
)
−
f
(
x
)
{\displaystyle \Delta y=f(x+\Delta x)-f(x)}
을 뜻하는 용어이며, 평균 변화율 (平均變化率, 영어 : average rate of change )은 두 증분의 비
Δ
y
Δ
x
=
f
(
x
+
Δ
x
)
−
f
(
x
)
Δ
x
{\displaystyle {\frac {\Delta y}{\Delta x}}={\frac {f(x+\Delta x)-f(x)}{\Delta x}}}
를 뜻하는 용어이다.[2] :211–212 미분 계수 (微分係數, 영어 : differential coefficient ) 또는 순간 변화율 (瞬間變化率, 영어 : instantaneous rate of change )은 평균 변화율의 극한
d
y
d
x
=
lim
Δ
x
→
0
Δ
y
Δ
x
=
lim
Δ
x
→
0
f
(
x
+
Δ
x
)
−
f
(
x
)
Δ
x
{\displaystyle {\frac {dy}{dx}}=\lim _{\Delta x\to 0}{\frac {\Delta y}{\Delta x}}=\lim _{\Delta x\to 0}{\frac {f(x+\Delta x)-f(x)}{\Delta x}}}
을 뜻하는 용어이다.[2] 좌극한 을 사용하면 좌미분 또는 좌미분 계수 (左微分係數)의 개념을 얻으며, 우극한 을 사용하면 우미분 또는 우미분 계수 (右微分係數)의 개념을 얻는다.
순간 속도 문제 [ 편집 ] 자유 낙하 과정을 스트로보스코프로 촬영하여 시간과 변위의 함수 관계를 구할 수 있으며, 여기에 미분을 취하면 (순간) 속도가 된다. 어떤 물체의 시간에 따른 변위
s
=
s
(
t
)
{\displaystyle s=s(t)}
t
∼
t
+
Δ
t
{\displaystyle t\sim t+\Delta t}
평균 속도
v
¯
{\displaystyle {\bar {v}}}
v
¯
=
Δ
s
Δ
t
=
s
(
t
+
Δ
t
)
−
s
(
t
)
Δ
t
{\displaystyle {\bar {v}}={\frac {\Delta s}{\Delta t}}={\frac {s(t+\Delta t)-s(t)}{\Delta t}}}
등속 운동 의 경우 각 시점의 빠르기는 서로 같으며, 이는 아무 부분의 평균 속도와도 같다. 하지만, 일반적인 물체의 운동은 변속 운동 이므로, 빠르기가 시간에 따라 변화한다. 이 경우 평균 속도는 각 시점의 빠르기를 정확하게 반영하지 못하므로, 순간 속도 라는 개념이 필요하게 된다. 평균 속도를 구하는 과정의 시간
Δ
t
{\displaystyle \Delta t}
Δ
t
→
0
{\displaystyle \Delta t\to 0}
v
(
t
)
=
lim
Δ
t
→
0
Δ
s
Δ
t
=
lim
Δ
t
→
0
s
(
t
+
Δ
t
)
−
s
(
t
)
Δ
t
{\displaystyle v(t)=\lim _{\Delta t\to 0}{\frac {\Delta s}{\Delta t}}=\lim _{\Delta t\to 0}{\frac {s(t+\Delta t)-s(t)}{\Delta t}}}
일반적인 함수에 대하여, 미분은 그 함수의 변화량과 독립 변수의 변화량의 비가, 변화량이 0에 가까워질 때 갖는 극한으로 정의된다. 이에 따라, 순간 속도
v
(
t
)
{\displaystyle v(t)}
s
(
t
)
{\displaystyle s(t)}
t
{\displaystyle t}
v
(
t
)
=
s
′
(
t
)
{\displaystyle v(t)=s'(t)}
또는
v
=
d
s
d
t
{\displaystyle v={\frac {ds}{dt}}}
와 같이 표기할 수 있다.
예를 들어, 다리 위에서 손에 쥐었던 농구 공을 가만히 놓아 떨어뜨렸을 때, 공기 저항이나 바람 의 영향이 크지 않다면, 농구공의 운동은 자유 낙하 이며, 그 변위는 다음과 같다.
h
=
1
2
g
t
2
{\displaystyle h={\frac {1}{2}}gt^{2}}
따라서, 그 순간 속도를 다음과 같이 구할 수 있다.[3]
v
=
d
h
d
t
=
lim
Δ
t
→
0
1
2
g
(
t
+
Δ
t
)
2
−
1
2
g
t
2
Δ
t
=
lim
Δ
t
→
0
(
g
t
+
1
2
g
Δ
t
)
=
g
t
{\displaystyle {\begin{aligned}v&={\frac {dh}{dt}}\\&=\lim _{\Delta t\to 0}{\frac {{\frac {1}{2}}g(t+\Delta t)^{2}-{\frac {1}{2}}gt^{2}}{\Delta t}}\\&=\lim _{\Delta t\to 0}(gt+{\frac {1}{2}}g\Delta t)\\&=gt\end{aligned}}}
함수
f
:
I
→
R
{\displaystyle f\colon I\to \mathbb {R} }
I
{\displaystyle I}
열린구간 )의 점
a
∈
I
{\displaystyle a\in I}
미분
f
′
(
a
)
{\displaystyle f'(a)}
극한 이다.
f
′
(
a
)
=
lim
x
→
a
f
(
x
)
−
f
(
a
)
x
−
a
=
lim
Δ
x
→
0
f
(
a
+
Δ
x
)
−
f
(
a
)
Δ
x
{\displaystyle {\begin{aligned}f'(a)&=\lim _{x\to a}{\frac {f(x)-f(a)}{x-a}}\\&=\lim _{\Delta x\to 0}{\frac {f(a+\Delta x)-f(a)}{\Delta x}}\end{aligned}}}
이러한 극한은 존재하지 않을 수 있다. 이 극한이 존재하는 경우,
f
{\displaystyle f}
a
{\displaystyle a}
미분가능 하다고 한다. 미분의 기호는
f
′
(
a
)
{\displaystyle f'(a)}
D
f
(
a
)
{\displaystyle Df(a)}
d
f
d
x
(
a
)
{\displaystyle {\frac {df}{dx}}(a)}
[4] :217–218
좌미분과 우미분 [ 편집 ] 함수
f
:
(
b
,
a
]
→
R
{\displaystyle f\colon (b,a]\to \mathbb {R} }
a
{\displaystyle a}
좌미분 (左微分, 영어 : left derivative )
f
−
′
(
a
)
{\displaystyle f'_{-}(a)}
좌극한 이다.
f
−
′
(
a
)
=
lim
x
→
a
−
f
(
x
)
−
f
(
a
)
x
−
a
=
lim
Δ
x
→
0
−
f
(
a
+
Δ
x
)
−
f
(
a
)
Δ
x
{\displaystyle {\begin{aligned}f'_{-}(a)&=\lim _{x\to a^{-}}{\frac {f(x)-f(a)}{x-a}}\\&=\lim _{\Delta x\to 0^{-}}{\frac {f(a+\Delta x)-f(a)}{\Delta x}}\end{aligned}}}
마찬가지로, 함수
f
:
[
a
,
c
)
→
R
{\displaystyle f\colon [a,c)\to \mathbb {R} }
a
{\displaystyle a}
우미분 (右微分, 영어 : right derivative )
f
+
′
(
a
)
{\displaystyle f'_{+}(a)}
우극한 이다.
f
+
′
(
a
)
=
lim
x
→
a
+
f
(
x
)
−
f
(
a
)
x
−
a
=
lim
Δ
x
→
0
+
f
(
a
+
Δ
x
)
−
f
(
a
)
Δ
x
{\displaystyle {\begin{aligned}f'_{+}(a)&=\lim _{x\to a^{+}}{\frac {f(x)-f(a)}{x-a}}\\&=\lim _{\Delta x\to 0^{+}}{\frac {f(a+\Delta x)-f(a)}{\Delta x}}\end{aligned}}}
미분과 좌미분과 우미분의 관계는 극한과 좌극한과 우극한의 관계와 유사하다. 좌미분과 우미분은 존재하지 않을 수 있으며, 모두 존재하더라도 서로 같지 않을 수 있다. 만약 좌미분과 우미분이 모두 존재하며 서로 같다면, 그 점에서의 미분 역시 존재하게 된다.
미분가능 함수 [ 편집 ] 열린구간
(
a
,
b
)
{\displaystyle (a,b)}
f
:
(
a
,
b
)
→
R
{\displaystyle f\colon (a,b)\to \mathbb {R} }
f
{\displaystyle f}
(
a
,
b
)
{\displaystyle (a,b)}
미분가능 함수 라고 한다.
f
{\displaystyle f}
x
∈
(
a
,
b
)
{\displaystyle x\in (a,b)}
닫힌구간
[
a
,
b
]
{\displaystyle [a,b]}
f
:
[
a
,
b
]
→
R
{\displaystyle f\colon [a,b]\to \mathbb {R} }
f
{\displaystyle f}
[
a
,
b
]
{\displaystyle [a,b]}
미분가능 함수 라고 한다.
f
{\displaystyle f}
x
∈
(
a
,
b
)
{\displaystyle x\in (a,b)}
f
{\displaystyle f}
a
{\displaystyle a}
f
{\displaystyle f}
b
{\displaystyle b}
비슷하게, 임의의 유형의 구간에서의 미분가능 함수를 정의할 수 있다. 즉, 구간에서의 미분가능 함수는 내부점에서 미분가능하며, 구간에 속하는 왼쪽 끝점에서 우미분이 존재하며, 구간에 속하는 오른쪽 끝점에서 좌미분이 존재하는 함수이다.
도함수 [ 편집 ] 함수 f (x ) = x sinx 2 + 1의 도함수는 f' = sinx 2 + 2x 2 cosx 2 이다. 미분 가능 함수
f
:
I
→
R
{\displaystyle f\colon I\to \mathbb {R} }
I
{\displaystyle I}
구간 )가 주어졌다고 하자. 그렇다면, 임의의 점
x
∈
I
{\displaystyle x\in I}
f
{\displaystyle f}
x
{\displaystyle x}
f
′
(
x
)
{\displaystyle f'(x)}
f
{\displaystyle f}
도함수 라고 하거나, 똑같이 미분 이라고 한다. 즉,
f
{\displaystyle f}
f
′
{\displaystyle f'}
f
′
:
I
→
R
{\displaystyle f'\colon I\to \mathbb {R} }
f
′
:
x
↦
lim
I
∋
y
→
x
f
(
y
)
−
f
(
x
)
y
−
x
{\displaystyle f'\colon x\mapsto \lim _{I\ni y\to x}{\frac {f(y)-f(x)}{y-x}}}
함수
f
{\displaystyle f}
f
′
{\displaystyle f'}
D
f
{\displaystyle Df}
d
f
d
x
{\displaystyle {\frac {df}{dx}}}
고계 도함수 [ 편집 ] 함수
f
:
I
→
R
{\displaystyle f\colon I\to \mathbb {R} }
I
{\displaystyle I}
n
{\displaystyle n}
f
(
n
)
{\displaystyle f^{(n)}}
f
{\displaystyle f}
n
{\displaystyle n}
n
{\displaystyle n}
n
{\displaystyle n}
n
{\displaystyle n}
영어 :
n
{\displaystyle n}
f
(
n
)
=
f
″
⋯
′
⏞
n
{\displaystyle f^{(n)}=f^{\overbrace {''\cdots '} ^{n}}}
즉, 이는 다음과 같다.
(영계 도함수/미분 , 零階導函數/微分, 영어 : zeroth derivative )
f
(
0
)
=
f
{\displaystyle f^{(0)}=f}
(일계 도함수/미분 , 一階導函數/微分, 영어 : first derivative )
f
(
0
)
{\displaystyle f^{(0)}}
I
{\displaystyle I}
f
(
1
)
=
f
(
0
)
′
=
f
′
{\displaystyle f^{(1)}={f^{(0)}}'=f'}
f
(
1
)
{\displaystyle f^{(1)}}
(이계 도함수/미분 , 二階導函數/微分, 영어 : second derivative )
f
(
1
)
{\displaystyle f^{(1)}}
I
{\displaystyle I}
f
(
2
)
=
f
(
1
)
′
=
f
″
{\displaystyle f^{(2)}={f^{(1)}}'=f''}
f
(
2
)
{\displaystyle f^{(2)}}
f
″
{\displaystyle f''}
D
2
f
{\displaystyle D^{2}f}
d
2
f
d
x
2
{\displaystyle {\frac {d^{2}f}{dx^{2}}}}
[5] :39
(삼계 도함수/미분 , 三階導函數/微分, 영어 : third derivative )
f
(
2
)
{\displaystyle f^{(2)}}
I
{\displaystyle I}
f
(
3
)
=
f
(
2
)
′
=
f
‴
{\displaystyle f^{(3)}={f^{(2)}}'=f'''}
f
(
3
)
{\displaystyle f^{(3)}}
f
‴
{\displaystyle f'''}
D
3
f
{\displaystyle D^{3}f}
d
3
f
d
x
3
{\displaystyle {\frac {d^{3}f}{dx^{3}}}}
...
(
n
{\displaystyle n}
n
{\displaystyle n}
영어 :
n
{\displaystyle n}
f
(
n
−
1
)
{\displaystyle f^{(n-1)}}
I
{\displaystyle I}
f
(
n
)
=
f
(
n
−
1
)
′
=
f
″
⋯
′
⏞
n
{\displaystyle f^{(n)}={f^{(n-1)}}'=f^{\overbrace {''\cdots '} ^{n}}}
f
(
n
)
{\displaystyle f^{(n)}}
n
{\displaystyle n}
f
(
n
)
{\displaystyle f^{(n)}}
D
n
f
{\displaystyle D^{n}f}
d
n
f
d
x
n
{\displaystyle {\frac {d^{n}f}{dx^{n}}}}
... 이러한
f
(
n
)
{\displaystyle f^{(n)}}
n
≥
3
{\displaystyle n\geq 3}
f
{\displaystyle f}
고계 도함수 또는 고계 미분 라고 한다.
함수
f
:
I
→
R
{\displaystyle f\colon I\to \mathbb {R} }
I
{\displaystyle I}
f
′
{\displaystyle f'}
f
′
{\displaystyle f'}
I
{\displaystyle I}
연속 함수 라면,
f
{\displaystyle f}
I
{\displaystyle I}
연속 미분 가능 함수
C
1
{\displaystyle {\mathcal {C}}^{1}}
f
{\displaystyle f}
k
{\displaystyle k}
f
(
k
)
{\displaystyle f^{(k)}}
f
{\displaystyle f}
C
k
{\displaystyle {\mathcal {C}}^{k}}
f
{\displaystyle f}
f
(
1
)
,
f
(
2
)
,
f
(
3
)
,
…
{\displaystyle f^{(1)},f^{(2)},f^{(3)},\dots }
f
{\displaystyle f}
매끄러운 함수
C
∞
{\displaystyle {\mathcal {C}}^{\infty }}
해석 함수
C
ω
{\displaystyle {\mathcal {C}}^{\omega }}
테일러 급수 가 자기 자신으로 수렴하는 함수이다. 이 경우,
k
{\displaystyle k}
C
k
−
1
{\displaystyle {\mathcal {C}}^{k-1}}
C
k
{\displaystyle {\mathcal {C}}^{k}}
라이프니츠의 표기법 [ 편집 ] 고트프리트 빌헬름 라이프니츠 는 도함수를 미분 계수를 통해 표기하였다. 이 표기에서, 도함수의 표기는 다음 가운데 하나이다.
d
y
d
x
=
d
f
d
x
=
d
d
x
f
{\displaystyle {\frac {dy}{dx}}={\frac {df}{dx}}={\frac {d}{dx}}f}
또한, 점에서의 미분의 표기는 다음 가운데 하나이다.
d
f
d
x
|
x
=
a
=
d
f
d
x
(
a
)
=
d
d
x
f
(
a
)
{\displaystyle \left.{\frac {df}{dx}}\right|_{x=a}={\frac {df}{dx}}(a)={\frac {d}{dx}}f(a)}
또한, 고계 도함수의 표기는 다음 가운데 하나이다.
d
n
y
d
x
n
=
d
n
f
d
x
n
=
d
n
d
x
n
f
{\displaystyle {\frac {d^{n}y}{dx^{n}}}={\frac {d^{n}f}{dx^{n}}}={\frac {d^{n}}{dx^{n}}}f}
어떤 미분 법칙들은 라이프니츠 표기법으로 표기할 경우 더 기억하기 쉽다. 예를 들어, 연쇄 법칙 을 다음과 같이 표기할 수 있다.[6] :142–144
d
y
d
x
=
d
y
d
u
⋅
d
u
d
x
{\displaystyle {\frac {dy}{dx}}={\frac {dy}{du}}\cdot {\frac {du}{dx}}}
기호
d
y
{\displaystyle dy}
미적분학 에서, 이는 선형 주요 부분 을 뜻한다. 비표준 해석학 에서, 이는 일종의 무한소로 정의된다. 미분기하학 에서, 이는 외미분 을 뜻한다.
라그랑주의 표기법 [ 편집 ] 조제프루이 라그랑주 는 도함수를 함수 기호의 오른쪽 위에 프라임 부호 를 써서 표기하였다. 즉, 도함수·이계 도함수·삼계 도함수·고계 도함수의 표기는 각각 다음과 같다.
f
(
1
)
=
f
′
{\displaystyle f^{(1)}=f'}
f
(
2
)
=
f
″
{\displaystyle f^{(2)}=f''}
f
(
3
)
=
f
‴
{\displaystyle f^{(3)}=f'''}
f
(
n
)
=
f
″
⋯
′
⏞
n
{\displaystyle f^{(n)}=f{\overbrace {''{}^{\cdots }{'}} ^{n}}}
뉴턴의 표기법 [ 편집 ] 아이작 뉴턴 은 도함수를 함수 위에 점을 찍어 표기하였다. 즉, 일계·이계·삼계·사계·고계 도함수의 표기는 각각 다음과 같다.
y
.
1
=
y
˙
{\displaystyle {\overset {\overset {1}{.}}{y}}={\dot {y}}}
y
.
2
=
y
¨
{\displaystyle {\overset {\overset {2}{.}}{y}}={\ddot {y}}}
y
.
3
=
y
.
.
.
=
y
¨
˙
{\displaystyle {\overset {\overset {3}{.}}{y}}={\overset {...}{y}}={\dot {\ddot {y}}}}
y
.
4
=
y
.
.
.
.
=
y
¨
¨
{\displaystyle {\overset {\overset {4}{.}}{y}}={\overset {....}{y}}={\ddot {\ddot {y}}}}
y
.
n
{\displaystyle {\overset {\overset {n}{.}}{y}}}
뉴턴의 표기법은 주로 물리학 에서 시간 변수에 대한 미분을 표기하는 데 사용된다. 이는 고계 도함수를 나타내기 힘겨운 표기법이지만, 시간에 대한 미분은 보통 이계를 넘지 않는 편이다.
오일러의 표기법 [ 편집 ] 레온하르트 오일러 는 도함수를 미분 연산자 를 통해 표기하였다. 즉, 일계·고계 도함수의 표기는 각각 다음과 같다.
D
f
{\displaystyle Df}
D
n
f
{\displaystyle D^{n}f}
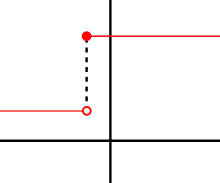
미분 가능성 [ 편집 ] 이 함수는 0을 도약 불연속점으로 하므로, 0에서 미분 가능하지 않다. 미분 가능 함수는 항상 연속 함수 이다. (이는 연속 함수가 아니라면, 독립 변숫값이 0에 가까워질 때 함숫값이 0에 가까워지지 않으므로, 이 둘의 비가 유한한 값으로 수렴하지 못하기 때문이다.) 그러나 연속 함수는 미분 가능 함수가 아닐 수 있다.
열린구간
I
{\displaystyle I}
f
:
I
→
R
{\displaystyle f\colon I\to \mathbb {R} }
a
∈
I
{\displaystyle a\in I}
f
′
(
a
)
{\displaystyle f'(a)}
f
{\displaystyle f}
a
{\displaystyle a}
f
+
′
(
a
)
=
f
−
′
(
a
)
{\displaystyle f'_{+}(a)=f'_{-}(a)}
f
{\displaystyle f}
a
{\displaystyle a}
lim sup
x
→
a
f
(
x
)
−
f
(
a
)
x
−
a
=
lim inf
x
→
a
f
(
x
)
−
f
(
a
)
x
−
a
{\displaystyle \limsup _{x\to a}{\frac {f(x)-f(a)}{x-a}}=\liminf _{x\to a}{\frac {f(x)-f(a)}{x-a}}}
간단한 미분 법칙 [ 편집 ] 미분 가능 함수에 대하여, 다음과 같은 미분 법칙들이 성립한다.
(합의 법칙 )
(
f
(
x
)
+
g
(
x
)
)
′
=
f
′
(
x
)
+
g
′
(
x
)
{\displaystyle (f(x)+g(x))'=f'(x)+g'(x)}
(곱의 법칙 )
(
f
(
x
)
g
(
x
)
)
′
=
f
′
(
x
)
g
(
x
)
+
f
(
x
)
g
′
(
x
)
{\displaystyle (f(x)g(x))'=f'(x)g(x)+f(x)g'(x)}
(몫의 법칙 )
(
f
(
x
)
g
(
x
)
)
′
=
f
′
(
x
)
g
(
x
)
−
f
(
x
)
g
′
(
x
)
g
2
(
x
)
{\displaystyle \left({\frac {f(x)}{g(x)}}\right)'={\frac {f'(x)g(x)-f(x)g'(x)}{g^{2}(x)}}}
(연쇄 법칙 )
(
f
(
g
(
x
)
)
)
′
=
f
′
(
g
(
x
)
)
g
′
(
x
)
{\displaystyle (f(g(x)))'=f'(g(x))g'(x)}
(역함수 정리 ) 만약
f
{\displaystyle f}
f
′
(
x
)
≠
0
{\displaystyle f'(x)\neq 0}
f
−
1
′
(
x
)
=
1
f
′
(
f
−
1
(
x
)
)
{\displaystyle {f^{-1}}'(x)={\frac {1}{f'(f^{-1}(x))}}}
(음함수 정리 ) 만약 음함수
F
(
x
,
y
)
=
0
{\displaystyle F(x,y)=0}
F
{\displaystyle F}
F
y
≠
0
{\displaystyle F_{y}\neq 0}
y
x
=
−
F
x
(
x
,
y
)
F
y
(
x
,
y
)
{\displaystyle y_{x}=-{\frac {F_{x}(x,y)}{F_{y}(x,y)}}}
만약 매개 변수 함수
x
=
x
(
t
)
{\displaystyle x=x(t)}
y
=
y
(
t
)
{\displaystyle y=y(t)}
x
(
t
)
{\displaystyle x(t)}
y
(
t
)
{\displaystyle y(t)}
x
′
(
t
)
≠
0
{\displaystyle x'(t)\neq 0}
y
x
=
y
′
(
t
)
x
′
(
t
)
{\displaystyle y_{x}={\frac {y'(t)}{x'(t)}}}
만약 극좌표 함수
r
=
r
(
θ
)
{\displaystyle r=r(\theta )}
y
x
=
tan
θ
+
r
(
θ
)
/
r
′
(
θ
)
1
−
r
(
θ
)
tan
θ
/
r
′
(
θ
)
{\displaystyle y_{x}={\frac {\tan \theta +r(\theta )/r'(\theta )}{1-r(\theta )\tan \theta /r'(\theta )}}}
라이프니츠 표기법을 사용하면 다음과 같다.
(합의 법칙 )
d
(
f
+
g
)
d
x
=
d
f
d
x
+
d
g
d
x
{\displaystyle {\frac {d(f+g)}{dx}}={\frac {df}{dx}}+{\frac {dg}{dx}}}
(곱의 법칙 )
d
(
f
g
)
d
x
=
g
d
f
d
x
+
f
d
g
d
x
{\displaystyle {\frac {d(fg)}{dx}}=g{\frac {df}{dx}}+f{\frac {dg}{dx}}}
(몫의 법칙 )
d
d
x
f
g
=
1
g
2
(
g
d
f
d
x
−
f
d
g
d
x
)
{\displaystyle {\frac {d}{dx}}{\frac {f}{g}}={\frac {1}{g^{2}}}\left(g{\frac {df}{dx}}-f{\frac {dg}{dx}}\right)}
(연쇄 법칙 )
d
y
d
x
=
d
y
d
u
d
u
d
x
{\displaystyle {\frac {dy}{dx}}={\frac {dy}{du}}{\frac {du}{dx}}}
(역함수 정리 ) 만약
f
{\displaystyle f}
d
y
d
x
≠
0
{\displaystyle {\frac {dy}{dx}}\neq 0}
d
x
d
y
=
1
/
d
y
d
x
{\displaystyle {\frac {dx}{dy}}=1{\bigg /}{\frac {dy}{dx}}}
(음함수 정리 ) 만약 음함수
F
(
x
,
y
)
=
0
{\displaystyle F(x,y)=0}
F
{\displaystyle F}
F
y
≠
0
{\displaystyle F_{y}\neq 0}
d
y
d
x
=
−
∂
F
∂
x
/
∂
F
∂
y
{\displaystyle {\frac {dy}{dx}}=-{\frac {\partial F}{\partial x}}{\bigg /}{\frac {\partial F}{\partial y}}}
만약 매개 변수 함수
x
=
x
(
t
)
{\displaystyle x=x(t)}
y
=
y
(
t
)
{\displaystyle y=y(t)}
x
(
t
)
{\displaystyle x(t)}
y
(
t
)
{\displaystyle y(t)}
x
′
(
t
)
≠
0
{\displaystyle x'(t)\neq 0}
d
y
d
x
=
d
y
d
t
/
d
x
d
t
{\displaystyle {\frac {dy}{dx}}={\frac {dy}{dt}}{\bigg /}{\frac {dx}{dt}}}
단조성과의 관계 [ 편집 ] 함수의 일부 성질은 도함수 또는 고계 도함수를 통해 판정할 수 있다. 예를 들어, 단조성 과 도함수의 관계는 다음과 같다.
f
:
I
→
R
{\displaystyle f\colon I\to \mathbb {R} }
I
{\displaystyle I}
f
{\displaystyle f}
증가 함수 일 필요충분조건은 임의의
x
∈
I
{\displaystyle x\in I}
f
′
(
x
)
≥
0
{\displaystyle f'(x)\geq 0}
f
{\displaystyle f}
감소 함수 일 필요충분조건은 임의의
x
∈
I
{\displaystyle x\in I}
f
′
(
x
)
≤
0
{\displaystyle f'(x)\leq 0}
f
{\displaystyle f}
엄격 증가 함수 일 필요충분조건은 임의의
x
∈
I
{\displaystyle x\in I}
f
′
(
x
)
≥
0
{\displaystyle f'(x)\geq 0}
J
⊆
I
{\displaystyle J\subseteq I}
f
′
(
x
)
≠
0
{\displaystyle f'(x)\neq 0}
x
∈
J
{\displaystyle x\in J}
f
{\displaystyle f}
엄격 감소 함수 일 필요충분조건은 임의의
x
∈
I
{\displaystyle x\in I}
f
′
(
x
)
≤
0
{\displaystyle f'(x)\leq 0}
J
⊆
I
{\displaystyle J\subseteq I}
f
′
(
x
)
≠
0
{\displaystyle f'(x)\neq 0}
x
∈
J
{\displaystyle x\in J}
극값과의 관계 [ 편집 ] 또한, 극값 과 도함수의 관계는 다음과 같다.
f
:
I
→
R
{\displaystyle f\colon I\to \mathbb {R} }
I
{\displaystyle I}
I
{\displaystyle I}
I
∖
{
a
}
{\displaystyle I\setminus \{a\}}
만약 어떤 빠진 근방
J
∖
{
a
}
⊆
I
{\displaystyle J\setminus \{a\}\subseteq I}
x
∈
J
∖
{
a
}
{\displaystyle x\in J\setminus \{a\}}
f
′
(
x
)
(
x
−
a
)
<
0
{\displaystyle f'(x)(x-a)<0}
f
(
a
)
{\displaystyle f(a)}
엄격 극댓값 이다.
만약 어떤 빠진 근방
J
∖
{
a
}
⊆
I
{\displaystyle J\setminus \{a\}\subseteq I}
x
∈
J
∖
{
a
}
{\displaystyle x\in J\setminus \{a\}}
f
′
(
x
)
(
x
−
a
)
>
0
{\displaystyle f'(x)(x-a)>0}
f
(
a
)
{\displaystyle f(a)}
엄격 극솟값 이다.
f
:
I
→
R
{\displaystyle f\colon I\to \mathbb {R} }
I
{\displaystyle I}
n
{\displaystyle n}
I
{\displaystyle I}
0
=
f
(
1
)
(
a
)
=
f
(
2
)
(
a
)
=
⋯
=
f
(
n
−
1
)
(
a
)
{\displaystyle 0=f^{(1)}(a)=f^{(2)}(a)=\cdots =f^{(n-1)}(a)}
만약
n
{\displaystyle n}
f
(
n
)
(
a
)
≠
0
{\displaystyle f^{(n)}(a)\neq 0}
f
(
a
)
{\displaystyle f(a)}
만약
n
{\displaystyle n}
f
(
n
)
(
a
)
<
0
{\displaystyle f^{(n)}(a)<0}
f
(
a
)
{\displaystyle f(a)}
만약
n
{\displaystyle n}
f
(
n
)
(
a
)
>
0
{\displaystyle f^{(n)}(a)>0}
f
(
a
)
{\displaystyle f(a)}
볼록성과의 관계 [ 편집 ] 또한, 볼록성 과 도함수의 관계는 다음과 같다.
f
:
I
→
R
{\displaystyle f\colon I\to \mathbb {R} }
I
{\displaystyle I}
f
{\displaystyle f}
x
<
y
{\displaystyle x<y}
f
−
′
(
x
)
≤
f
+
′
(
x
)
≤
f
−
′
(
y
)
≤
f
+
′
(
y
)
{\displaystyle f'_{-}(x)\leq f'_{+}(x)\leq f'_{-}(y)\leq f'_{+}(y)}
f
{\displaystyle f}
오목 함수 일 필요충분조건은 어디서나 좌미분과 우미분이 존재하며, 임의의
x
<
y
{\displaystyle x<y}
f
−
′
(
x
)
≥
f
+
′
(
x
)
≥
f
−
′
(
y
)
≥
f
+
′
(
y
)
{\displaystyle f'_{-}(x)\geq f'_{+}(x)\geq f'_{-}(y)\geq f'_{+}(y)}
f
{\displaystyle f}
엄격 볼록 함수 일 필요충분조건은 어디서나 좌미분과 우미분이 존재하며, 임의의
x
<
y
{\displaystyle x<y}
f
−
′
(
x
)
≤
f
+
′
(
x
)
<
f
−
′
(
y
)
≤
f
+
′
(
y
)
{\displaystyle f'_{-}(x)\leq f'_{+}(x)<f'_{-}(y)\leq f'_{+}(y)}
f
{\displaystyle f}
엄격 오목 함수 일 필요충분조건은 어디서나 좌미분과 우미분이 존재하며, 임의의
x
<
y
{\displaystyle x<y}
f
−
′
(
x
)
≥
f
+
′
(
x
)
>
f
−
′
(
y
)
≥
f
+
′
(
y
)
{\displaystyle f'_{-}(x)\geq f'_{+}(x)>f'_{-}(y)\geq f'_{+}(y)}
도함수는 연속 함수가 아닐 수 있지만, 도함수는 충분히 좋은 성질들을 갖췄으며, 다음과 같다.
(다르부 정리 ) 도함수는 중간값 성질을 만족시킨다.
도함수의 연속점은 조밀하다.
어떤 함수가 만약 임의의 도함수의 왼쪽에 합성되었을 때 도함수가 된다면, 이 함수는 일차 함수 이다. 미분표 문서를 참고하십시오.
제곱 함수의 그래프바이어슈트라스 함수 는 모든 점에서 연속이면서 모든 점에서 미분 불가능한 병적 함수의 예이다.절댓값 함수는 0을 지나는 직선 가운데 접선과 유사한 성질을 갖는 것들은 기울기가 [-1, 1]에 속하는 직선들이며, 이는 유일하지 않다.세제곱근 함수의 0에서의 접선은 기울기가 무한대인 수직선이다.f (x ) = x sin(1/x ) (x ≠ 0); f (0) = 0와 같이 정의되는 함수의, 0을 지나는 할선의 기울기는 -1과 1 사이에서 심하게 요동친다.정의를 통한 계산 [ 편집 ] 함수
f
(
x
)
=
x
2
{\displaystyle f(x)=x^{2}}
f
′
(
x
)
=
lim
Δ
x
→
0
f
(
x
+
Δ
x
)
−
f
(
x
)
Δ
x
=
lim
Δ
x
→
0
(
x
+
Δ
x
)
2
−
x
2
Δ
x
=
lim
Δ
x
→
0
x
2
+
2
x
Δ
x
+
(
Δ
x
)
2
−
x
2
Δ
x
=
lim
Δ
x
→
0
2
x
Δ
x
+
(
Δ
x
)
2
Δ
x
=
lim
Δ
x
→
0
(
2
x
+
Δ
x
)
=
2
x
{\displaystyle {\begin{aligned}f'(x)&=\lim _{\Delta x\to 0}{\frac {f(x+\Delta x)-f(x)}{\Delta x}}\\&=\lim _{\Delta x\to 0}{\frac {(x+\Delta x)^{2}-x^{2}}{\Delta x}}\\&=\lim _{\Delta x\to 0}{\frac {x^{2}+2x\Delta x+(\Delta x)^{2}-x^{2}}{\Delta x}}\\&=\lim _{\Delta x\to 0}{\frac {2x\Delta x+(\Delta x)^{2}}{\Delta x}}\\&=\lim _{\Delta x\to 0}(2x+\Delta x)\\&=2x\end{aligned}}}
초등 함수 [ 편집 ] 몇 가지 기본적인 실수 초등 함수 의 (자연 정의역 에서의) 미분은 다음과 같다.
(상수 함수 )
(
C
)
′
=
0
{\displaystyle (C)'=0}
(멱함수 )
(
x
α
)
′
=
α
x
α
−
1
(
α
∈
R
)
{\displaystyle (x^{\alpha })'=\alpha x^{\alpha -1}\qquad (\alpha \in \mathbb {R} )}
(지수 함수 )
(
e
x
)
′
=
e
x
{\displaystyle (e^{x})'=e^{x}}
(지수 함수 )
(
a
x
)
′
=
a
x
ln
a
(
a
>
0
)
{\displaystyle (a^{x})'=a^{x}\ln a\qquad (a>0)}
(로그 함수 )
(
ln
x
)
′
=
1
x
{\displaystyle (\ln x)'={\frac {1}{x}}}
(로그 함수 )
(
log
a
x
)
′
=
1
x
ln
a
(
a
>
0
,
a
≠
1
)
{\displaystyle (\log _{a}x)'={\frac {1}{x\ln a}}\qquad (a>0,\;a\neq 1)}
(삼각 함수 )
(
sin
x
)
′
=
cos
x
{\displaystyle (\sin x)'=\cos x}
(삼각 함수 )
(
cos
x
)
′
=
−
sin
x
{\displaystyle (\cos x)'=-\sin x}
(삼각 함수 )
(
tan
x
)
′
=
sec
2
x
{\displaystyle (\tan x)'=\sec ^{2}x}
(삼각 함수 )
(
cot
x
)
′
=
−
csc
2
x
{\displaystyle (\cot x)'=-\csc ^{2}x}
(삼각 함수 )
(
sec
x
)
′
=
sec
x
tan
x
{\displaystyle (\sec x)'=\sec x\tan x}
(삼각 함수 )
(
csc
x
)
′
=
−
csc
x
cot
x
{\displaystyle (\csc x)'=-\csc x\cot x}
(역삼각 함수 )
(
arcsin
x
)
′
=
1
1
−
x
2
{\displaystyle (\arcsin x)'={\frac {1}{\sqrt {1-x^{2}}}}}
(역삼각 함수 )
(
arccos
x
)
′
=
−
1
1
−
x
2
{\displaystyle (\arccos x)'=-{\frac {1}{\sqrt {1-x^{2}}}}}
(역삼각 함수 )
(
arctan
x
)
′
=
1
1
+
x
2
{\displaystyle (\arctan x)'={\frac {1}{1+x^{2}}}}
(역삼각 함수 )
(
arccot
x
)
′
=
−
1
1
+
x
2
{\displaystyle (\operatorname {arccot} x)'=-{\frac {1}{1+x^{2}}}}
(역삼각 함수 )
(
arcsec
x
)
′
=
1
|
x
|
x
2
−
1
{\displaystyle (\operatorname {arcsec} x)'={\frac {1}{|x|{\sqrt {x^{2}-1}}}}}
(역삼각 함수 )
(
arccsc
x
)
′
=
−
1
|
x
|
x
2
−
1
{\displaystyle (\operatorname {arccsc} x)'=-{\frac {1}{|x|{\sqrt {x^{2}-1}}}}}
(쌍곡선 함수 )
(
sinh
x
)
′
=
cosh
x
{\displaystyle (\sinh x)'=\cosh x}
(쌍곡선 함수 )
(
cosh
x
)
′
=
sinh
x
{\displaystyle (\cosh x)'=\sinh x}
(쌍곡선 함수 )
(
tanh
x
)
′
=
sech
2
x
{\displaystyle (\tanh x)'=\operatorname {sech} ^{2}x}
(쌍곡선 함수 )
(
coth
x
)
′
=
−
csch
2
x
{\displaystyle (\coth x)'=-\operatorname {csch} ^{2}x}
(쌍곡선 함수 )
(
sech
x
)
′
=
−
sech
x
tanh
x
{\displaystyle (\operatorname {sech} x)'=-\operatorname {sech} x\tanh x}
(쌍곡선 함수 )
(
csch
x
)
′
=
−
csch
x
coth
x
{\displaystyle (\operatorname {csch} x)'=-\operatorname {csch} x\coth x}
(역쌍곡선 함수 )
(
arsinh
x
)
′
=
1
x
2
+
1
{\displaystyle (\operatorname {arsinh} x)'={\frac {1}{\sqrt {x^{2}+1}}}}
(역쌍곡선 함수 )
(
arcosh
x
)
′
=
1
x
2
−
1
{\displaystyle (\operatorname {arcosh} x)'={\frac {1}{\sqrt {x^{2}-1}}}}
(역쌍곡선 함수 )
(
artanh
x
)
′
=
1
1
−
x
2
{\displaystyle (\operatorname {artanh} x)'={\frac {1}{1-x^{2}}}}
(역쌍곡선 함수 )
(
arcoth
x
)
′
=
1
1
−
x
2
{\displaystyle (\operatorname {arcoth} x)'={\frac {1}{1-x^{2}}}}
(역쌍곡선 함수 )
(
arsech
x
)
′
=
−
1
x
1
−
x
2
{\displaystyle (\operatorname {arsech} x)'=-{\frac {1}{x{\sqrt {1-x^{2}}}}}}
(역쌍곡선 함수 )
(
arcsch
x
)
′
=
−
1
|
x
|
1
+
x
2
{\displaystyle (\operatorname {arcsch} x)'=-{\frac {1}{|x|{\sqrt {1+x^{2}}}}}}
미분 가능성 [ 편집 ] 바이어슈트라스 함수 는 연속 함수 이지만, 어디서도 미분 가능하지 않다.
절댓값 함수
|
x
|
{\displaystyle |x|}
립시츠 연속 함수 이며, 0이 아닌 어디서나 미분 가능하지만, 0이 첨점 (좌미분과 우미분이 존재하지만 서로 다른 점)이므로 0에서 미분 가능하지 않다.[4] :217–218
(
|
x
|
)
′
=
sgn
x
(
x
≠
0
)
{\displaystyle (|x|)'=\operatorname {sgn} x\qquad (x\neq 0)}
(
|
x
|
)
+
′
|
x
=
0
=
1
{\displaystyle (|x|)'_{+}|_{x=0}=1}
(
|
x
|
)
−
′
|
x
=
0
=
−
1
{\displaystyle (|x|)'_{-}|_{x=0}=-1}
세제곱근 함수
x
3
{\displaystyle {\sqrt[{3}]{x}}}
(
x
3
)
′
=
{
1
3
x
2
3
x
≠
0
∞
x
=
0
{\displaystyle ({\sqrt[{3}]{x}})'={\begin{cases}{\frac {1}{3{\sqrt[{3}]{x^{2}}}}}&x\neq 0\\\infty &x=0\end{cases}}}
함수
{
x
sin
1
x
x
≠
0
0
x
=
0
{\displaystyle {\begin{cases}x\sin {\frac {1}{x}}&x\neq 0\\0&x=0\end{cases}}}
는 연속 함수이며, 0이 아닌 어디서나 미분 가능하지만, 극한
lim
x
→
0
x
sin
1
x
−
0
x
−
0
=
lim
x
→
0
sin
1
x
{\displaystyle \lim _{x\to 0}{\frac {x\sin {\frac {1}{x}}-0}{x-0}}=\lim _{x\to 0}\sin {\frac {1}{x}}}
가 존재하지 않으므로 0에서 미분 가능하지 않다.
미분 가능 함수가 아닌 절대 연속 함수와 모든 부분 구간에서 단조 함수가 아닌 미분 가능 함수가 존재한다.
미분은 최적화 (변분법 )·미분 방정식 ·테일러 급수 에서 응용된다.
일반화 [ 편집 ] 다변수 벡터 함수의 경우 [ 편집 ] 일변수 실숫값 함수의 미분의 개념을 일반화하여 다변수 벡터 함수의 편미분 ·전미분 ·기울기 ·헤세 행렬 ·야코비 행렬 의 개념을 얻을 수 있다.
바나흐 공간 사이의 함수의 경우 [ 편집 ] 바나흐 공간
V
,
W
{\displaystyle V,W}
f
:
U
→
W
{\displaystyle f\colon U\to W}
U
⊆
V
{\displaystyle U\subseteq V}
열린집합 )의 점
a
∈
U
{\displaystyle a\in U}
프레셰 도함수 연속 선형 변환
D
a
f
:
V
→
W
{\displaystyle D_{a}f\colon V\to W}
[7]
lim
x
→
a
‖
f
(
x
)
−
f
(
a
)
−
D
a
f
(
x
−
a
)
‖
‖
x
−
a
‖
=
0
{\displaystyle \lim _{x\to a}{\frac {\Vert f(x)-f(a)-D_{a}f(x-a)\Vert }{\Vert x-a\Vert }}=0}
이러한 연속 선형 변환
D
a
f
{\displaystyle D_{a}f}
f
{\displaystyle f}
a
{\displaystyle a}
프레셰 미분 가능
V
=
R
{\displaystyle V=\mathbb {R} }
W
{\displaystyle W}
실수 바나흐 공간 인 경우, 다음 두 조건이 서로 동치이다.[7]
f
{\displaystyle f}
a
{\displaystyle a}
f
′
(
a
)
=
lim
x
→
a
f
(
x
)
−
f
(
a
)
x
−
a
∈
W
{\displaystyle f'(a)=\lim _{x\to a}{\frac {f(x)-f(a)}{x-a}}\in W}
또한, 이 경우
f
{\displaystyle f}
a
{\displaystyle a}
D
a
f
:
R
→
W
{\displaystyle D_{a}f\colon \mathbb {R} \to W}
[7]
D
a
f
(
Δ
x
)
=
Δ
x
f
′
(
a
)
{\displaystyle D_{a}f(\Delta x)=\Delta xf'(a)}
그 밖의 미분의 일반화에는 미분 연산자 ·미분 대수 ·두 매끄러운 다양체 사이의 미분 가능 함수 따위가 있다. 주로 볼록 함수에 대해서 하방미분 이라는 일반화 방법이 있다.
뉴턴은 변화량의 순간변화율이 곡선의 접선과 같다는 점을 발견하였다. 미분적분학 은 고대로 거슬러 올라간다. 대표적으로 크니도스의 에우독소스 와 고대 그리스 의 아르키메데스 , 중국의 유휘 등이 있다. 고대 수학자들은 대상을 잘게 나눠서 더하는 과정을 극한으로 하여 무한대와 무한소를 고려하며 원주율 을 구하고 구 와 원기둥 의 부피 를 계산하였다.[8] 케랄라 학파(Kerala school of astronomy and mathematics)가 테일러 급수 , 무한급수의 근사법, 수렴에 대한 적분판정법, 미분의 초기형태, 비선형 방정식 풀이를 위한 방법, 곡선 아래부분이 차지하는 넓이가 적분값과 같다는 이론 등 미적분을 위한 많은 요소들을 기술하였다. 17세기 프랑스 수학자 피에르 드 페르마 는 무한소를 다루는 adequality 개념을 도입하여, 함수의 미분을 하였고, 미분해서 함수의 극대와 극소를 찾는 법을 만들었다. 이탈리아 의 수학자 에반젤리스타 토리첼리 는 무한소의 개념(무한히 작은 단위량)을 도입하여 포물선 일부 구간의 면적을 구하는 방법을 정리하였다. 또한 거리와 속도의 관계를 밝혔고 넓이를 구하는 문제가 접선을 구하는 문제와 역관계가 있다는 것을 밝혔다.[9] :69–70
이후 아일랜드 수학자 제임스 그레고리 (James Gregory)가 미적분학의 핵심 정리인 미적분학 기본정리 의 증명을 출판하였으며, 영국 수학자 아이작 배로 (Issac Barrow)가 좀 더 일반적인 경우를 증명하였다. 무한소 미적분과 유한차 미적분의 결합은 두 번째 미적분학 기본정리 가 증명되고 2년이 지나서 존 월리스 (John Wallis), 아이작 배로 (Issac Barrow)와 제임스 그레고리 (James Gregory)에 의해 1670년경에 완성됐다.
아이작 뉴턴 과 라이프니츠 는 각각 독자적인 방법으로 미분적분학 에 기여하였다. 뉴턴은 기하학을 바탕으로 순간적인 변화량을 구하는 방법을 유율법(영어 : fluxion )이라고 불렀다. 뉴턴은 유율법을 곡선에 대한 접선과 곡률의 견지에서 파악하였다. 뉴턴은 1687년 《자연 철학의 수학적 원리》에 유율법을 발표하였다. 한편, 라이프니츠는 함수 f(x)에서 x가 무한히 작은 증분인 미분(영어 : differential )의 변화량을 가질 때 f(x)의 변화량을 구하는 방법으로서 미분을 하였다. 라이프니츠는 1677년 무렵에는 미분의 계산방법과 표기법을 완성하였다. 오늘날에는 보다 수학적으로 효율적인 라이프니츠의 방법이 주로 쓰인다.[6] :102–141
뉴턴과 라이프니츠는 미분에 대한 업적을 놓고 오랫동안 다투었으며 이로 인해 유럽의 수학계는 둘 중 누구를 지지하는 가를 놓고 심한 대립을 보이기도 하였다. 뉴턴과 라이프니츠는 서로 상대방이 자신의 아이디어를 훔쳤다고 비판하였다. 이러한 대립은 라이프니츠가 사망한 이후에도 계속되었다. 오늘날에는 뉴턴과 라이프니츠가 각자 독자적인 방법으로 미분을 발견했다고 본다.[6]
‘미분(微分)’이란 말은 작게 자른다는 뜻이다. ‘미분’이란 번역어를 근대에 처음 쓴 문헌은 엘리어스 루미스 (영어판 ) 알렉산더 와일리 (영어판 ) 이선란 이 번역한 《대미적습급(代微積拾級)》이다. 한편 조지프 니덤 은 《중국의 과학과 문명 (영어판 ) [10]
외부 링크 [ 편집 ]


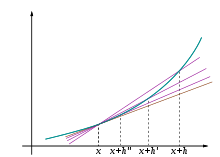





















































![{\displaystyle f\colon (b,a]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac43d0d26d5d1018c11178b4784863b201275d0b)








![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
![{\displaystyle f\colon [a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5ab61178bf5349838758ffe3d96135406ed0245)





































































































































![{\displaystyle {\sqrt[{3}]{x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a55f866116e7a86823816615dd98fcccde75473)
![{\displaystyle ({\sqrt[{3}]{x}})'={\begin{cases}{\frac {1}{3{\sqrt[{3}]{x^{2}}}}}&x\neq 0\\\infty &x=0\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/758afc3e579bac7937f393ded46d4018ef6b84d5)













