조화급수 (harmonic series) 란 각 항의 역수 가 등차수열 을 이루는 급수 로, 다음의 발산하는 무한급수 를 가리킨다.
∑
k
=
1
∞
1
k
=
1
1
+
1
2
+
1
3
+
1
4
+
⋯
.
{\displaystyle \sum _{k=1}^{\infty }{\frac {1}{k}}={\frac {1}{1}}+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+\cdots .\!}
조화급수라는 명칭은 배음 또는 음악의 화성학 에서 유래되었다. 악기의 진동하는 현의 배음의 파장은 현의 기본 파장 의 1/2, 1/3, 1/4, ...에 해당하는 값이다. 첫 번째 값 이후에 나오는 모든 값들은 이웃 값의 조화 평균 이다. 조화 평균이라는 명칭 또한 음악에서 유래하였다.
조화급수가 발산한다는 사실은 14세기 니콜 오렘 에 의해 처음 증명되었으나, 이 발견은 세상에서 잊혀졌다. 그 후 17세기 피에트로 멩골리(Pietro Mengoli), 요한 베르누이 , 야코프 베르누이 에 의해 다시 증명되었다.
역사적으로 조화급수는 건축가들에게 특히 인기 있었다. 이러한 경향은 바로크 시대에 특히 강해서, 건축가들은 교회와 궁전을 건축할 때 평면도 및 입면도상의 비례와 건물 내·외부간의 건축 디테일의 조화를 위해 조화급수를 사용하였다.[1]
발산성 [ 편집 ] 수열 각각의 항은 점차 0 에 가까워지고 있음에도 불구하고, 총합은 무한대로 발산한다. 발산하는 속도는 매우 느려서
ln
n
{\displaystyle \ln n}
조화수열 과 자연로그 의 오차의 극한을 나타내는 상수로 오일러-마스케로니 상수 가 있다). 조화급수는 최초
10
43
{\displaystyle 10^{43}}
비교판정법 [ 편집 ] 니콜 오렘 의 가장 유명한 발산 증명으로
2
n
{\displaystyle 2^{n}}
∑
k
=
1
∞
1
k
=
1
+
[
1
2
]
+
[
1
3
+
1
4
]
+
[
1
5
+
1
6
+
1
7
+
1
8
]
+
[
1
9
+
⋯
]
+
⋯
>
1
+
[
1
2
]
+
[
1
4
+
1
4
]
+
[
1
8
+
1
8
+
1
8
+
1
8
]
+
[
1
16
+
⋯
]
+
⋯
=
1
+
1
2
+
1
2
+
1
2
+
1
2
+
⋯
{\displaystyle {\begin{aligned}\sum _{k=1}^{\infty }{\frac {1}{k}}&{}=1+\left[{\frac {1}{2}}\right]+\left[{\frac {1}{3}}+{\frac {1}{4}}\right]+\left[{\frac {1}{5}}+{\frac {1}{6}}+{\frac {1}{7}}+{\frac {1}{8}}\right]+\left[{\frac {1}{9}}+\cdots \right]+\cdots \\&{}>1+\left[{\frac {1}{2}}\right]+\left[{\frac {1}{4}}+{\frac {1}{4}}\right]+\left[{\frac {1}{8}}+{\frac {1}{8}}+{\frac {1}{8}}+{\frac {1}{8}}\right]+\left[{\frac {1}{16}}+\cdots \right]+\cdots \\&{}=1+\ {\frac {1}{2}}\ \ \ +\quad {\frac {1}{2}}\ \quad +\ \qquad \quad {\frac {1}{2}}\qquad \ \quad \ +\quad \ \ {\frac {1}{2}}\ \quad +\ \cdots \end{aligned}}}
=
1
+
0.5
+
0.5
+
0.5
+
0.5
+
⋯
{\displaystyle \;\;\;\;\;\;\;\;=1+0.5+0.5+0.5+0.5+\cdots }
=
1
+
1
+
1
+
⋯
{\displaystyle \;\;\;\;\;\;=1+1+1+\cdots }
조화급수보다 작은 급수가 발산하므로, 조화급수도 발산하게 된다.
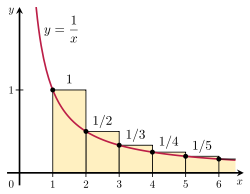
적분판정법 [ 편집 ] 적분판정법 으로도 간단하게 발산함을 증명할 수 있다.
조화급수는 우측 그림에서 색칠한 사각형들의 넓이를 모두 더한 것이 된다.
그런데 만약 곡선
y
=
1
/
x
{\displaystyle y=1/x}
조화급수의 최초
k
{\displaystyle k}
∑
k
=
1
∞
1
k
{\displaystyle \textstyle \sum _{k=1}^{\infty }{\frac {1}{k}}}
k
+
1
{\displaystyle k+1}
∫
1
k
+
1
1
x
d
x
{\displaystyle \int _{1}^{k+1}{\frac {1}{x}}\,dx\;}
∫
1
∞
1
x
d
x
=
lim
k
→
∞
∫
1
k
+
1
1
x
d
x
=
lim
k
→
∞
ln
(
k
+
1
)
=
∞
{\displaystyle \int _{1}^{\infty }{\frac {1}{x}}\,dx\;=\;\lim _{k\to \infty }\int _{1}^{k+1}{\frac {1}{x}}\,dx\;=\;\lim _{k\to \infty }\ln(k+1)=\infty }
따라서 적분 판정법에 의해 조화급수도 동시에 발산하게 된다.
잘 알려진 성질 [ 편집 ] 이 무한급수는 리만 제타 함수 에 1을 대입했을 때 얻어지는 수열이다. 따라서 리만 제타 함수는 1에서 특이점을 가지게 된다.
부호를 번갈아가며 쓴 교대조화급수(alternating harmonic series)는 수렴한다. 그 수렴 값은
ln
2
{\displaystyle \ln 2}
절대 수렴 하지 않는다. 따라서, 교대조화급수의 경우 항을 재배치하여 원하는 어떤 실수 값이든 만들어낼 수 있다.
같이 보기 [ 편집 ]
↑ George L. Hersey (2002년 12월 1일). 《Architecture and Geometry in the Age of the Baroque》. University Of Chicago Press. 11-12, 37-51쪽. ISBN 0226327841





![{\displaystyle {\begin{aligned}\sum _{k=1}^{\infty }{\frac {1}{k}}&{}=1+\left[{\frac {1}{2}}\right]+\left[{\frac {1}{3}}+{\frac {1}{4}}\right]+\left[{\frac {1}{5}}+{\frac {1}{6}}+{\frac {1}{7}}+{\frac {1}{8}}\right]+\left[{\frac {1}{9}}+\cdots \right]+\cdots \\&{}>1+\left[{\frac {1}{2}}\right]+\left[{\frac {1}{4}}+{\frac {1}{4}}\right]+\left[{\frac {1}{8}}+{\frac {1}{8}}+{\frac {1}{8}}+{\frac {1}{8}}\right]+\left[{\frac {1}{16}}+\cdots \right]+\cdots \\&{}=1+\ {\frac {1}{2}}\ \ \ +\quad {\frac {1}{2}}\ \quad +\ \qquad \quad {\frac {1}{2}}\qquad \ \quad \ +\quad \ \ {\frac {1}{2}}\ \quad +\ \cdots \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18b1003a191cc2345d1dc4d6877d3994a7411c07)









