코시 열
이 문서는 자연스럽지 않게 번역되었으며, 기계 번역을 통해 작성되었을 수도 있습니다. (2022년 3월) |
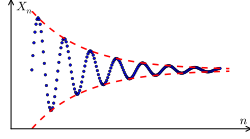
코시 열(Cauchy列, 영어: Cauchy sequence)은 해석학에서 점 사이의 거리가 서로 점점 가까워지는 수열이다. 프랑스의 수학자인 오귀스탱 루이 코시에서 이름을 따서 명명되었다.[1] 보다 정확히 말하면 작은 양수의 거리가 주어진 경우에 수열의 유한한 수의 원소를 제외한 모든 원소가 서로 주어진 거리보다 작다.
각 항이 "이전" 항에 임의로 근접하는 것은 충분하지 않다. 예를 들어 자연수의 제곱근 수열은 다음과 같다.
연속 항은 다음과 같이 임의로 서로 가까워진다.
그러나 지수 n의 값이 증가함에 따라 an 항은 임의로 커지게 된다. 따라서 모든 지수 n과 거리 d에 대해 am – an > d과 같이 충분히 큰 지수 m이 존재한다. 실제로 m > (√n + d)2이면 충분하다. 결과적으로, 얼마나 멀리 가더라도 수열의 나머지 항은 서로 가까워지지 않으므로 수열은 코시 열이 아니다.
코시 열의 효용성은 완비 거리 공간(모든 그러한 수열이 극한으로 수렴한다고 알려진 곳)[2]에서 수열의 수렴 기준이 극한을 사용하는 정의와는 다르게 수열의 항 자체에만 의존하는 점에 있다. 이는 이론 및 응용 알고리즘에서 종종 이용되는데 반복적 프로세스는 반복법으로 구성된 코시 열을 생성하기 위해 상대적으로 쉽게 보여질 수 있으며 따라서 종료와 같은 논리적 조건을 충족시킨다.
보다 추상적인 균등 공간에서 코시 열은 코시 필터와 코시 그물의 형태로 일반화 할 수 있다.
실수에서의 활용[편집]
실수의 수열 이 있다고 하자. 모든 양수인 ε에 대해 양의 정수 N이 있어서, 모든 자연수 m, n > N이 다음 조건을 만족한다면, 이 수열을 코시 열이라고 부른다.
여기서 수직 막대는 절댓값을 나타낸다. 비슷한 방법으로 유리수나 복소수의 코시 열을 정의할 수 있다. 코시는 이러한 조건을 무한대인 m, n의 모든 쌍에 대해 이 무한소가 되는 것으로 공식화했다.
실수 r의 경우에는 r의 잘린 소수 확장 수열은 코시 열을 형성한다. 예를 들어 r = π일 때 이 수열은 (3, 3.1, 3.14, 3.141, ...)이다. m < n을 가정할 때 m번째와 n번째 항은 최대 101−m만큼 달라지며 m이 커짐에 따라 고정된 양수 ε보다 작아진다.
코시 수렴 계수[편집]
만약 가 집합 의 수열인 경우에는 수열에 대한 "코시 수렴 계수"는 자연수 집합에서 자신에게 와 같은 함수 이다.
코시 수렴 계수가 있는 모든 수열은 코시 열이다. 코시 열을 위한 계수의 존재는 자연수의 순서적 특성에서 비롯된다 (는 코시 열의 정의에서 가능한 가장 작은 이 되도록 하여 을 로 한다). 또한 계수의 존재는 선택 공리의 약한 형태인 의존적 선택 공리로부터 따르며 또한 AC00이라고 불리는 훨씬 더 약한 조건으로부터 온다. "정규 코시 열"은 주어진 코시 수렴 계수(보통 또는 )의 수열이다. 코시 수렴 계수를 갖는 모든 코시 열은 정규 코시 열과 동일하다. 이것은 어떠한 형태의 선택 공리도 사용하지 않고 증명될 수 있다.
코시 수렴 계수는 어떠한 형태의 선택도 사용하지 않으려는 구성주의 수학자들에 의해 사용된다. 코시 수렴 계수를 사용하면 구성주의 해석학에서 정의와 이론을 모두 단순화할 수 있다. 정규 코시 열은 에렛 비숍(Errett Bishop)의 구성적 해석학 기초(Foundations of Constructive Analysis)에서, 더글러스 브리지(Douglas Bridges)의 비구성적 교과서(ISBN 978-0-387-98239-7)에서 사용되었다.
거리 공간에서의 활용[편집]
코시 열의 정의는 거리 개념만 포함하므로 이를 거리 공간 X로 일반화하는 것이 간단하다. 이를 위해 |xm − xn|은 xm과 xn 사이의 거리 d (xm, xn) (여기서 d는 거리를 나타냄)로 대체된다.
일반적으로 주어진 거리 공간 (X, d)의 수열은 x1, x2, x3, ...이다. 코시 열(d(xm, xn) < ε)은 모든 양의 실수 ε > 0인 경우 모든 양의 정수 m, n > N에 대해 거리d(xm, xn) < ε인 양의 정수 N이 있다는 것을 의미한다.
대략적으로 말해서 수열의 항은 X에 극한이 있어야 한다는 것을 암시하는 방식으로 점점 더 가까워지고 있다. 그럼에도 불구하고 그러한 극한은 항상 X 내에 존재하는 것은 아니다. 모든 코시 열이 공간에서 수렴하는 공간의 속성을 완비성이라고 하며 아래에 자세히 설명되어 있다.
완비성[편집]
모든 코시 열이 X의 원소로 수렴되는 거리 공간(X, d)을 완비 거리 공간이라고 한다.
예시[편집]
실수는 일반적인 절댓값에 의해 유도된 거리 아래에서 완비이며 실수의 구성 가운데 유리수의 코시 열을 포함한다. 이 구조에서 특정한 꼬리 행동을 가진 유리수의 코시 열의 각 동치류, 즉 서로 임의로 가까워지는 수열의 모임은 실수이다.
다소 다른 유형의 예는 이산 위상을 가진 거리 공간 X이다. X 원소의 모든 코시 열은 어떤 지점 이후에는 값이 일정해야 하며, 결국 반복해서 등장하는 값으로 수렴한다.
예시가 아닌 경우: 유리수[편집]
유리수 Q는 일반적인 거리에서 완비가 아니다. 무리수 R에 수렴하는 일련의 유리수들이 있는데 이들은 Q에 극한이 없는 코시 열들이다. 실수 x가 무리수인 경우에 n번째 항이 x의 소수점 확장에서 n번째 항이 잘린 소수점 자리인 수열(xn)은 무리수인 극한 x를 가진 유리수의 코시열을 제공한다. 무리수는 확실히 R에 존재한다. 예를 들면 다음과 같다.
- 에 의해 정의된 수열은 정의로부터 유리수로만 구성된 수열임이 명확하지만, 이는 바빌로니아 법으로 를 임의의 정밀도로 근사하는 수열이므로 수열은 어떤 유리수로 수렴하지 않는다.
- 연속된 피보나치 수의 비의 수열인 는 만약 그것이 수렴한다면 를 만족하는 극한 로 수렴하는데, 어떤 유리수도 이 성질을 가지고 있지 않다. 그러나 이것을 실수 수열으로 생각한다면 무리수인 황금비 로 수렴한다.
- 지수, 사인, 코사인 함수 exp(x), sin(x), cos(x)의 값은 x≠0인 모든 유리수의 값에 대해 무리수인 것으로 알려져 있지만 각각 테일러 급수를 사용하는 유리수의 코시 열의 극한으로 정의될 수 있다.
예시가 아닌 경우: 열린 구간[편집]
R에 보통 거리가 있는 실수의 집합에서 열린 구간 는 완비 공간이 아니다. 그 안에 수열 이 있는데 이것은 코시 열(임의적으로 작은 거리 경계 의 경우 의 모든 항 이 구간에 적합하다)이다. 그러나 "극한"인 수 은 공간 에 속하지 않는다.
그 외의 속성[편집]
- 모든 수렴 수열(극한 s 포함)은 코시 열로서 어떠한 고정된 지점을 넘어서 특정한 실수 ε > 0이 주어지면 수열의 모든 항은 s의 거리 ε/2 안에 있기 때문에 수열의 특정한 두 항은 서로 거리 ε 안에 있다.
- 모든 거리 공간에서 코시 열 xn은 유계 함수이다 (일부 N의 경우 N번째 이후의 수열의 모든 항은 서로 거리 1 안에 있고 M이 xN과 N번째까지의 모든 항 사이의 가장 큰 거리라면 수열의 어떤 항도 xN으로부터 M + 1보다 큰 거리를 갖지 않는다.
- 임의의 거리 공간에서 극한 s와 수렴된 수열을 갖는 코시 열은 동일한 극한 그 자체로 수렴한다. 왜냐하면 원래 수열의 일부 고정점을 넘어서 임의의 실수 r > 0이 주어지기 때문에 수열의 모든 항은 s의 r/2 안에 있고 원래 수열의 두 항은 각각 거리 r/2 안에 있기 때문이다. 원래 수열의 모든 항은 s의 거리 r 안에 있다.
볼차노-바이어슈트라스 정리, 하이네-보렐 정리는 이들의 마지막 2가지 특성과 밀접하게 관련된 실수의 완비성에 대한 표준 증거를 제시한다. 실수의 코시 열은 유계이고 볼차노-바이어슈트라스 정리에 따라 수렴하는 부분 수열을 갖기 때문에 그 자체를 스스로 수렴한다. 실수의 완전성에 대한 이 증거는 암시적으로 최소 상계 성질을 이용한다. 위에서 언급한 유리수의 완성으로서 실수를 구성하는 대안적 접근 방식은 실수의 완전성을 자율적으로 만든다.
코시 열로 작업하고 완비성을 사용할 수 있는 이점을 보여주는 표준 삽화 가운데 하나는 무한히 연속되는 실수의 합계(또는 보다 일반적인 노름 공간 또는 바나흐 공간의 원소)를 고려하여 제공된다. 이러한 급수 은 부분합 의 수열이 수렴하는 경우에만 수렴하는 것으로 간주된다. 여기서 이라는 등식이 성립된다. 양수 p > q인 경우에는 이라는 등식을 통해 부분합의 수열이 코시 열인지 아닌지를 판단할 수 있다.
만약 가 거리 공간 M과 N 사이의 균등 연속 함수이고 (xn)가 M의 코시 열이라면, 는 N의 코시 열이다. 만약 와 가 유리수, 실수 또는 복소수에서 2개의 코시 열이라면, 합계 와 곱 역시 코시 열이다.
일반화[편집]
위상 벡터 공간[편집]
위상 벡터 공간 에 대한 코시 열의 개념도 있다. 먼저 0에 대한 국소기저인 의 를 선택한다. ()는 각 구성체가 일 때에 이 의 원소일 때에 코시 열이다. 의 위상 배치가 변환 불변 공간 와 호환된다면 2가지 정의는 일치한다.
위상군[편집]
코시 열의 위상 벡터 공간 정의는 연속적인 "추출" 연산만 있으면 되기 때문에 위상군의 맥락에서 설명될 수 있다. 위상군 의 수열 는 의 항등원의 모든 열린 근방 에 대해 이 존재할 때마다 를 따르는 일부 이 존재한다면 코시 열이다.
거리 공간의 완비화 구성과 마찬가지로 에 있는 모든 열린 근방 에 대해 이 을 따르도록 몇 개의 이 존재한다면 와 가 동등하다는 코시 열에 대한 이진 관계를 정의할 수 있다. 이러한 관계는 동치관계이고 이러한 수열은 반사적인 코시 열이다. 이러한 수열은 이기 때문에 대칭이며 이는 역의 연속성에 의해 항등원의 또다른 열린 근방이기 때문에 대칭이다. 에서 와 는 와 같이 항등원의 개방된 근방이기 때문에 추이적 관계이다. 이러한 쌍들은 군 연산의 연속성에 의해 존재한다.
군[편집]
군에는 코시 열 개념도 있다: 은 유한 지수 의 정규 부분군이 감소하는 수열이다. 의 수열 는 코시 열(w.r.t. )이라고 표현하는데 과 같은 인 경우에 이 있는 경우에만 해당된다. 기술적으로 이것은 의 위상 배치를 위한 코시 열과 동일하며 가 국소기저이다.
이러한 코시 열의 집합 는 (성분별 결과물인 경우) 군을 형성하며 Null 수열(s.th. )의 집합 은 의 정규 부분군이다. 요인 그룹 은 와 관련하여 의 완성이라고 한다. 그런 다음에 이러한 완비가 수열 의 역극한과 같은 형이라는 것을 확인할 수 있다.
정수론과 대수기하학에서 익숙한 이러한 구조의 예는 소수 p에 대한 p진수 완비 구조이다. 이 경우 G는 추가되는 정수이고 Hr은 pr의 정수 배수로 구성된 가법 부분군이다. 만약 가 공종 집합 수열이라면(즉 유한 지수의 모든 정규 부분군은 을 포함한다) 이 완비는 의 역극한과 동일하다는 점에서 표준이다. 여기서 는 유한 지수의 "모든" 정규 부분군에 걸쳐 변화한다.
초실수의 연속[편집]
실제 수열 은 일반적인 자연수 n 이외에 지수 n의 초정수 값에 대해 정의된 자연적인 초실수 확장 H를 갖고 있다. 무한대인 H와 K에 대해 값이 표시되는 경우()만 코시 열이다. 여기서 "st"는 표준부분함수이다.
코시 범주 완비[편집]
헤닝 크라우제(Henning Krause)는 2018년에 범주의 코시 완비화에 대한 개념을 도입했다. Q(유리수를 대상으로 하며, 작은 유리수에서 큰 유리수로의 사상을 가지는 얇은 범주)의 범주 코시 완비화는 R(마찬가지의 범주)이다.[3]
같이 보기[편집]
참고 문헌[편집]
- Bourbaki, Nicolas (1972년). 《Commutative Algebra》 영어 번역판. Addison-Wesley. ISBN 0-201-00644-8.
- Krause, Henning (2018년), 《Completing perfect complexes: With appendices by Tobias Barthel and Bernhard Keller》, arXiv:1805.10751, Bibcode:2018arXiv180510751B
- Lang, Serge (1993년), 《Algebra》 3판, Reading, Massachusetts: Addison-Wesley Pub. Co., ISBN 978-0-201-55540-0, Zbl 0848.13001
- Spivak, Michael (1994년). 《Calculus》 3판. Berkeley, CA: Publish or Perish. ISBN 0-914098-89-6. 2007년 5월 17일에 원본 문서에서 보존된 문서. 2007년 5월 26일에 확인함.
- Troelstra, Anne Sjerp; van Dalen, Dirk. 《Constructivism in Mathematics: An Introduction》. (건설적인 수학에 이용하기 위함)
- Reed, Michael; Barry Simon (1980년). 《Methods of Modern Mathematical Physics, Vol. 1: Functional Analysis》 2판. San Diego, California: Academic press inc. ISBN 0-12-585050-6.
각주[편집]
- ↑ Serge, Lang (1993년). 《Algebra》 3판. Reading, Massachusetts: Addison-Wesley Pub. Co. ISBN 978-0-201-55540-0. Zbl 0848.13001.
- ↑ Reed, Michael; Barry Simon (1980년). 《Methods of Modern Mathematical Physics, Vol. 1: Functional Analysis》 2판. San Diego, California: Academic press inc. 6쪽. ISBN 0-12-585050-6.
- ↑ Krause, Henning (2018년), 《Completing perfect complexes: With appendices by Tobias Barthel and Bernhard Keller》, arXiv:1805.10751, Bibcode:2018arXiv180510751B
외부 링크[편집]
- “Fundamental sequence”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4.