조화수열

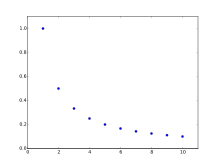
조화수열(harmonic progression)은 어떤 수열의 각 항의 역수들이 등차수열을 이룰 때이다. 다시 말해서, 다음 형태의 수열이다.

$a,\ {\frac {a}{1+d}},\ {\frac {a}{1+2d}},\ {\frac {a}{1+3d}}.$

조화급수(harmonic series)와는 다른 개념이다.

예

적당한 등차수열을 취해서 그 역수를 만들어 주면 간단히 만들 수 있다. 예를 들어 다음과 같은 수열이다.

• 1/1, 1/2, 1/3, 1/4
• 1, 1, 1, 1, 1
• 1/23461234, 1/23843963, 1/24226692, 1/24609421
• -1, -1/3, -1/5, -1/7

조화 중항

세 수 $a$, $b$, $c$가 이 순서로 조화수열을 이룰때, $b$는 $a$와 $c$의 조화 중항이라고 한다. 이 때, $b$는 $a$와 $c$의 조화 평균이 된다. 식으로 표현하면 다음과 같다.

$b={\frac {2ac}{a+c}}$

두 수 a, b가 모두 양수라면, 두 수의 조화 평균은 기하 평균보다 항상 작거나 같다. 기하 평균은 산술 평균보다 작거나 같으므로, 다음과 같은 연쇄적인 부등식이 성립한다.

$a$, $b$ 두 수가 모두 양수일 때, ${\frac {a+b}{2}}\geq {\sqrt {ab}}\geq {\frac {2ab}{a+b}}$가 성립한다.

무한합

조화수열의 무한합은 발산한다. 적분판정법으로 간단하게 확인할 수 있다.

같이 보기

• 등비수열
• 등차수열
• 조화급수