원주율
 3.1415926535897932384626433832795…… |
| 원주율 |
|---|
 |
| 이용 |
| 원넓이 · 원둘레 · 기타 이용 |
| 특성 |
| 무리수 · 초월수 |
| 유용성 |
| 22/7보다 작음증명 · 근사값 · 값 암기 |
| 관련 인물 |
|
아르키메데스 · 유휘 · 조충지 |
| 역사 |
| 연대기 · 원주율의 역사 |
| 원주율과 문화 |
| 입법 · 파이의 날 |
| 기타 |
| 원적문제 · 바젤 문제 · 파인만 포인트 · 기타 문서.. |
원주율(圓周率, 문화어: 원주률)은 원둘레와 지름의 비 즉, 원의 지름에 대한 둘레의 비율을 나타내는 수학 상수이다. 수학과 물리학의 여러 분야에 두루 쓰인다. 그리스 문자 π로 표기하고, 파이(π)라고 읽는다.[1] 원주율은 수학에서 다루는 가장 중요한 상수 가운데 하나이다.[2] 무리수인 동시에 초월수이다. 아르키메데스의 계산이 널리 알려져 있어 아르키메데스 상수라고 부르기도 하며, 독일에서는 1600년대 뤼돌프 판 쾰런이 소수점 이하 35자리까지 원주율을 계산한 이후 뤼돌프 수라고 부르기도 한다.[3] 원주율의 값은 순환하지 않는 무한소수(무리수)이기 때문에, 원주율을 포함한 계산에서는 3.14 또는 3.141 등 첫 소수점 아랫자리를 취한 근삿값을 사용하거나 기호 파이(π)를 사용한다.
개요[편집]

유클리드 평면에서 원은 크기와 관계없이 언제나 닮은 도형이다. 따라서 원의 지름에 대한 둘레의 비는 언제나 일정하며, 이를 원주율이라 한다. 즉, 원의 지름을 d, 둘레를 C라 하면 원주율 π는 다음의 식으로 나타낼 수 있다.[4]
원주율을 나타내는 기호 π는 1706년 영국의 수학자 윌리엄 존스가 최초로 사용했다. 이것은 둘레를 뜻하는 고대 그리스어 "페리페레스"(περιφηρής) 또는 "페리메트론"(περίμετρον)의 첫 글자를 딴 것이다.[5] 윌리엄 존스는 “특정 도형의 길이나 넓이를 구하는 계산에 매우 유용한 방법이 여러 가지 있다. 원을 예로 들면 지름이 1인 원의 둘레를 약 3.14159…= π로 표기하는 것이다.”라고 기호 π의 사용을 제안하였다.[6]
원주율은 소수점 아래 어느 자리에서도 끝나지 않고, 순환마디도 없이 무한히 계속되는 비순환소수이다. 원주율이 무리수라는 것은 1761년 요한 하인리히 람베르트가 증명했다. 원주율의 소수점 이하에서 나타나는 수열은 무작위 표집을 통해 만드는 난수표와 성질이 같다.[7] 원주율은 십진법으로는 값을 정확하게 표기할 수 없기 때문에 실제 계산에서는 근삿값을 이용한다.




한편, 원주율은 계수가 유리수인 유한 차수 다항식의 해가 될 수 없다. 이러한 종류의 수를 초월수라 부른다. 이 사실은 1882년 페르디난트 폰 린데만이 증명하였다. 여기에서 원주율은 어떤 정수에 적당한 유리수를 곱하고 제곱근을 씌우는 등의 연산을 조합하여 얻어낼 수 없다는 사실을 알 수 있다. 또한 원주율이 초월수라는 사실을 통해, 그리스 3대 난제 중 하나였던 “자와 컴퍼스만을 사용하여 원과 넓이가 같은 정사각형을 작도하는 원적문제”가 유한한 대수적 방법으로는 불가능하다는 것을 증명할 수 있다.
유클리드 기하학에서 원과 원주율의 관계를 살펴보면 다음과 같은 사실을 확인할 수 있다.[8]:183
- 원의 둘레를 구하는 식은 원주율의 정의와 같다.
- 원의 둘레 = 지름 × 원주율
- 원의 넓이를 구하는 방법은 아르키메데스 시대 이후 여러 가지 기법이 알려져 있다. 널리 사용하는 방법 가운데 하나는 레오나르도 다빈치가 고안한 것으로, 정육각형을 이용한 구적법이다. 레오나르도 다빈치는 왼쪽 그림과 같이 정육각형을 이용하여 분할한 원을 직사각형으로 치환하여 원의 넓이를 계산하였다.[9]
- 원의 넓이 = 원주율 × 반지름2
원주율이 보이는 복잡한 수열에 비해 이를 계산하는 방법은 의외로 단순하다. 라이프니츠가 정리한 다음 계산식이 널리 알려져 있다.
역사[편집]
고대[편집]
고대의 여러 문화에서 원주율의 값으로 3이 쓰였다. 고대 메소포타미아에서도 원주율을 3으로 계산하였고[10], 구약성경 열왕기상 7장 23절과 역대하 4장 2절에는 직경과 둘레의 길이를 기술하여 원주율이 3정도 임을 알고 있었다고 추측된다. 고대 중국의 수학책인 《구장산술》에서도 3을 원주율로 제시하였다. 《구장산술》에는 다음과 같은 문제가 실려 있다.[11]
| 원문 | 번역 |
|---|---|
| 今有圓田周三十步經十步問爲田幾何 答曰七十五步 |
둘레가 30걸음, 지름이 10걸음인 원 모양의 밭이 있다면 넓이는 얼마인가? 답: 75걸음² |
| 원주율의 근삿값을 3.14로 할 때 오늘날의 계산은
| |
구장산술의 계산은 평균값으로 이루어져있다. (1) 원둘레가 30보인 경우 반지름은 30=2r*3.14 r=4.78 이경우의 면적은 71.74 (2) 지름이 10보인 경우 면적은 78.5. (1)과 (2)의 평균은 75보. 그러므로 구장산술의 계산이 부정확하다는 것은 잘못되었다.

구장산술에 실린 계산이 매우 부정확하다는 것은 왼쪽 그림을 보면 쉽게 알 수 있다. 지름이 1인 원에 내접하는 정육각형의 둘레는 3이고 실제 원의 둘레는 그것과는 차이가 상당하기 때문이다.[12] 이는 고대에서부터 이미 널리 알려진 문제였고 값을 보다 정확하게 구하기 위한 노력이 계속되었다. 고대 이집트에서는 원통형 바퀴를 굴려 직접 측정해 원주율을 계산하였는데 256⁄81=3.16049……를 사용하였다.[10]

한편 기원전 3세기의 고대 그리스 수학자 아르키메데스는 근대 적분이 없었던 당시에 무한소라는 개념을 사용하였다. 그는 소거법을 사용하여 의 근삿값을 계산하였다. 이 방법은 임의 차원의 미지항에 대해 극한을 취하는 것으로, 귀류법을 사용하여 동일한 계산을 반복하는 과정을 통해 해답을 얻는 것이다. 아르키메데스는 변이 매우 많은 다각형이 임의의 원에 내접하는 경우와 외접하는 경우를 비교하여 원주율을 계산하였다. 즉, 임의의 원의 둘레는 그것에 외접하는 다각형의 둘레보다 짧고 내접하는 다각형보다 길다. 이때 다각형의 변이 많아질수록 외접하는 경우와 내접하는 경우의 둘레 차는 작아지므로 원의 둘레에 근사한다. 즉, 지름이 d인 원에 내접하는 변의 개수가 n인 정다각형의 둘레 Pn에 대해 다음과 같이 함수의 극한을 취하면 원주율을 얻을 수 있다.
아르키메데스는 정구십육각형을 이용하여 의 값을 다음과 같이 계산하였다.[13]
아르키메데스는 이 결과에 따라 의 근삿값으로 3.1416을 제시하였다. 또한, 아르키메데스는 원의 면적이 임을 증명하였다. 아르키메데스는 자신의 저서 《구와 원기둥》에서 어떠한 크기가 주어지더라도 임의의 크기에 적당한 수를 곱하여 주어진 크기를 초과할 수 있다고 가정하였다. 이를 실수에서의 아르키메데스 성질이라고 한다.[14]
중국의 삼국시대 위나라 수학자 유휘는 《구장산술》에 주해를 달아 다시 출판하였는데, 아르키메데스와 같은 방법을 사용하여 원주율을 157⁄50=3.14 로 계산하였다. 유휘가 계산한 원주율 근삿값은 오늘날에도 일상생활에서 사용한다.[15]
2세기에 들어 중국의 장형은 원주율을 3.1623으로 계산하였고[16] 5세기 중국 남북조 시대 송나라의 조충지는 3.141592로 계산하였다.[17] 독일에서는 1600년대 뤼돌프 판 쾰런이 소수점 이하 35자리까지 계산하였다.[3] 컴퓨터를 도입하기 이전에 가장 긴 자리수의 원주율을 계산한 사람은 영국의 수학자 샹크스였다. 그는 15년이나 걸려 1873년까지 소수점 이하 707자리까지 원주율 값을 계산해냈다. 하지만 후에 그 계산은 528자리까지만 정확한 것으로 밝혀졌다.[18]
컴퓨터를 통한 원주율 계산[편집]
1949년 9월 최초로 컴퓨터를 이용하여 70시간에 걸쳐 소수점 아래 2,037자리까지 계산하였다. 원주율 계산에 컴퓨터를 도입한 이후 원주율 계산은 단순 알고리즘의 무한 반복에 불과한 작업이 되어 수학적 의미를 잃었다.[19] 이 계산은 종종 컴퓨터의 성능을 시험하기 위한 방법으로 사용한다.[18] 2005년 일본 도쿄 대학의 가네다 야스마사 교수는 컴퓨터를 601시간 56분 동안 사용하여 원주율을 소수점 1,241,100,000,000자리까지 구하였다. 2009년 〈도쿄신문〉에 따르면, 일본 쓰쿠바 대학 계산과학연구센터는 17일, 슈퍼컴퓨터를 사용한 원주율 계산에서, 2조 5769억 8037만 자리수의 세계기록을 수립했다고 한다. (73시간 59분 소요)[20][21] 그 이후 프랑스에서는 2조 7천억 자리까지 계산하였다.[22] 2010년 8월 3일에는 일본의 회사원 곤도 시게루(近藤茂)가 소수점 이하 5조 자리까지 계산하였다. (90일 7시간 소요, 검증 기간 포함 / PC 사용)[23] 2016년 11월 11일 스위스의 입자 물리학자인 페터 트뤼프(Peter Trüb)는 105일 동안 계산하여, 원주율을 소수점 이하 22조 4591억 5771만 8361자리(조 개)까지 계산했다.[24]
원주율의 값[편집]
값의 소수점 아래 1,000자리 수는 다음과 같다.
3.1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989...
수학적 특성[편집]
원주율은 두 정수의 비로 나타낼 수 없는 무리수이다. 또한, 계수가 유리수인 다항식의 근이 될 수 없는 초월수이다.
무리수[편집]
원주율이 무리수라는 것은 1761년에 요한 하인리히 람베르트가 증명했다.[25] 람베르트는 다음과 같이 탄젠트 함수의 연분수 전개식을 이용하여 이를 증명하였다.[26]
가 이 아닌 유리수일 때 위에 전개된 연분수를 십진기수법으로 나타내면 언제나 순환하지 않는 소수이므로 항상 무리수이다. 한편, 이므로 는 반드시 무리수여만 한다. 따라서 역시 무리수이다.[27][주해 1]
초월수[편집]
원주율이 초월수임은 오일러 등식을 이용하여 다음과 같이 증명할 수 있다.[28] 오일러 등식은,
- …… (1)[주해 2]
이다. 이 때 π가 정계수 대수방정식 의 근이라면 이다. 따라서 역시 성립하여야 한다. 이제 y=iπ라 하면 π=-iy 이고 -π=iy 이므로, iπ는 다음 식으로 나타낼 수 있는 정계수 대수방정식을 만족시켜야 한다.
이제 을 ν차원의 방정식이라 하면 그 근인 y1, y2,……, yν에는 iπ가 존재하여야 하므로, 식 (1)에 따라 다음과 같이 나타낼 수 있다.
그런데 이러한 관계를 만족하는 대수방정식의 근이 유리수라고 가정하면 무한히 약분할 수 있어서, 이를 기약분수로 표현할 수 없는 모순이 생긴다.[주해 3] 유리수를 기약분수로 표현할 수 없다는 것은 유리수의 정의에 어긋나므로 π가 정계수 대수방정식 의 근이라는 최초의 가정이 잘못되었다고 볼 수밖에 없다. 즉, 원주율은 초월수이다. 자세한 증명은 링크한 주석을 참고하기 바란다.[29]
수열[편집]
개요에서 밝혔듯이 원주율은 반복되지 않고 무한히 계속되는 수열을 이룬다. 네덜란드 수학자 라위트전 브라우어르는 다음과 같은 질문을 제기하였다.[30]
- 원주율 π = 3.141592……의 전개에서 계속되는 소수의 수열에 9가 연속적으로 100회 나타날까?
브라우어르는 이 수열이 무한히 계속되기 때문에 이 수열을 어느 정도까지만 확인한 결과만으로는 위 질문에 답할 수 없다는 점을 지적하였다. 실제 소수점 이하 762번째에서부터 수열 999999 가 출현한다. 이 수열은 파인만 포인트로 알려져 있으며 원주율의 소수점 이하 수열에서 확률 0.08%로 발견할 수 있는 것으로 알려져 있다.[31] 따라서 경험적 방법으로는 위 문제에 답할 수 없다. 브라우어르는 이러한 논의를 바탕으로 아리스토텔레스의 배중률[주해 4] 은 유한한 개수를 대상으로 한 것에만 적용 수 있을 뿐 무한한 것에 적용할 수 없다고 결론지었다.[30]
원주율에서 나타나는 수열은 무작위 표집을 사용해 만든 난수표의 성질을 보인다. 하지만, 실제 원주율의 수열이 완전한 무작위성을 보이는지는 증명되지 않았다.[7]
계산식[편집]
원주율은 무리수이기 때문에 그 값은 근삿값으로밖에 알 수 없다. 대부분의 계산에는 3.14나 22/7 라는 근삿값을 사용해도 충분하다. 355/113은 외우기 좋고, 정밀도도 좋다. 좀 더 정밀한 기술의 계산에서는 3.1416 또는 3.14159 등을 사용하기도 한다. 기상 예보나 인공 위성 등의 계산에는 소수점 아래 30자리까지 나아간 근삿값을 사용하고 있다. 이렇게 불규칙적인 패턴을 가지는 원주율은 다음과 같이 규칙적인 수식을 이용하여 계산할 수 있다. 더 정확한 값을 얻으려면 수식을 연장하기만 하면 된다.[19]
위 식은 고트프리트 빌헬름 라이프니츠가 전개한 것으로 흔히 라이프니츠의 공식이라고 부른다. 이 식 외에도 원주율을 계산하는 공식으로는 다음과 같은 것이 있다.[32]
- …… 월리스 공식 1655년
- ……오일러의 곱셈 공식 1735년[주해 5]
17세기의 프랑스 수학자 프랑수아 비에트는 다음과 같은 무한급수로 원주율을 계산하였다.[33][34]
또한, 스털링 근사를 사용해 원주율을 유도할 수도 있다.[35]
원주율은 다음과 같이 연분수로 표현할 수 있다.[36]
1996년 데이빗 베일리는 피터 보어와인, 시몽 플루프와 공동으로 π에 관련된 새로운 무한급수를 발견했다.
이 식을 이용하면 2진수 그리고 16진수로 표기한 π값의 소수점 아래 n자리 값을 n-1째 자리까지 구하지 않고 바로 계산해 낼 수 있다. 베일리의 홈페이지 에선 다양한 프로그래밍 언어를 이용해 구현한 실제 예를 볼 수 있다.
적용[편집]
원주율은 수학과 물리학 등 여러 분야에서 다양하게 적용한다.
기하학[편집]
아르키메데스는 원과 구의 다음과 같은 성질을 증명하였다.[37]
한편, 원은 이심률이 0인 타원으로 간주할 수 있으며 이에 따라 타원 방정식은 일반적으로 다음과 같이 표현한다.[38]:70
이 때 타원의 넓이를 A라 하면 다음과 같이 계산할 수 있다.

각의 크기를 나타내는 무차원 단위인 라디안은 오른쪽 그림과 같이 정의하여 반지름과 호의 길이가 같을 때 1라디안이 된다. 따라서, 원 전체는 2π라디안이고 이를 도로 환산하면 다음과 같다.[38]:119
- π라디안 = 180°
바젤 문제[편집]
1687년 스위스의 바젤의 수학 교수였던 야코프 베르누이와 요한 베르누이 형제는 조화급수가 발산한다는 사실을 증명하였다. 그러나, 조화급수의 각 분모를 제곱한 다음 식을 닫힌 형식으로 나타내는 것에는 실패하였으며 논문의 끝에 이 문제를 해결하였다면 알려주기 바란다고 적었다.
당대의 유명한 수학자들이 이 문제를 풀기 위해 시도하였으나 결국 실패하였고, 이 문제는 바젤 문제로 알려지며 해석학자의 악몽으로까지 불리게 되었다. 이를 해결한 사람은 레온하르트 오일러로 1735년에 이 급수의 값이 다음과 같다는 것을 증명하였다.
후일 이 급수는 다음과 같은 일반식으로 표현되었는데 이것이 리만 제타 함수이다.[39]
리만 제타 함수는 s가 짝수일 때 위 식을 이용하여 그 값을 쉽게 계산할 수 있으나 홀수일 때는 자명하지 않다. 1978년 s가 3일 때 무리수로 수렴하는 것이 증명되었다. 이 수렴값은 아페리 상수라고 한다.[40]
복소수 계산[편집]

복소수 는 극좌표계를 이용하여 다음과 같이 나타낼 수 있다.[41]
복소해석학에서 π는 복소수 변수가 지수 함수에서 보이는 행동과 연관이 있으며 오일러의 공식에 따라 다음과 같이 표현할 수 있다.
i는 허수 단위이기 때문에 i2 = −1 이므로 이를 π라디안(=180°)과 함께 자연로그의 밑 e의 지수로 표현하면 다음과 같은 오일러 등식을 얻는다.
따라서 n 번째 단위근은 다음과 같다.
이제 가우스 적분으로 나타내면,
이 결과는 반정수의 감마 함수가 √π의 유리수 곱임을 뜻한다.
확률과 통계[편집]

확률과 통계에서 원주율이 등장하는 정리들은 다음과 같은 것들이 있다.
이 된다.[42]
- 참고로, 모든 확률 밀도 함수는 다음과 같이 적분한다.[44]
조르주루이 르클레르 드 뷔퐁이 제기한 뷔퐁의 바늘 문제는 원주율의 근삿값을 구하는 경험주의적인 방법으로 거론된다. 길이가 L인 바늘을 일정 간격으로 그린 평행선에 떨어뜨린다고 가정해 보자. 이 때 평행선의 간격 S가 바늘의 길이보다 크다고 하면, 바늘을 떨어뜨린 횟수 n번에 대해 바늘이 평행선 밖으로 나간 횟수 x번(단, x>0)에는 몬테카를로 방법에 의해 다음과 같은 관계가 있다.[45]
즉, 뷔퐁의 바늘 문제에서 바늘을 떨어뜨리는 횟수가 매우 많아지면 바늘이 평행선을 벗어나는 횟수에 대한 바늘을 떨어뜨린 전체 횟수의 비는 원주율에 근사한다.
물리학[편집]
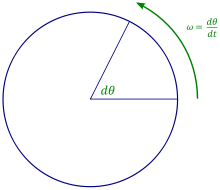
원주율 자체는 물리 상수가 아니지만 물리학의 여러 분야에서 두루 사용한다. 이는 자연 현상의 상당수가 원과 관계가 있기 때문이다. 예를 들어 회전수를 일정하게 유지하는 등속원운동에서 각속도와 원주속도는 다음과 같이 계산할 수 있다.[46]
- 각속도를 ω (= θ / 초), 분당 회전수를 N이라 하면
- 이때, 반지름을 r이라 하면 원주속도 v는
이 외에 물리학에서 원주율을 사용하는 경우는 다음과 같다.
- 불확정성 원리에 따라, 양자 역학적인 물리량은 동시에 정확히 관찰할 수 없다. 예를 들어 입자의 특정 위치를 Δ x라 하고 이 때의 운동량을 Δ p 라 하면, 이 둘의 크기를 둘 다 정확히 관찰할 수는 없으며 다음 식을 사용해 확률적으로만 계산한다.[47]
같이 보기[편집]
주해[편집]
참고[편집]
- ↑ 송은영, 재미있는 수학상식, 맑은창, 2007, ISBN 89-86607-59-X, 126-133 쪽
- ↑ Pickover, Clifford A. (2005). A passion for mathematics: numbers, puzzles, madness, religion, and the quest for reality. John Wiley and Sons. p. 52. ISBN 0-471-69098-8., Extract of page 52
- ↑ 가 나 파이(π) 본격 연구는 아르키메데스부터 Archived 2012년 12월 9일 - 웨이백 머신, 사이언스타임즈, 2010년 1월 20일
- ↑ "About Pi". Ask Dr. Math FAQ. Retrieved 2007-10-29.
- ↑ Stein, Sherman (2006). 《아르키메데스》. 번역 이우영. 경문사. 170쪽. ISBN 89-7282-926-9.
- ↑ Smith, David Eugene. A source book in mathematics, Volume I, pp. 346-347.
- ↑ 가 나 Pi Seems A Good Random Number Generator But Not Always The Best, Science daily, 2005-4-25
- ↑ Rudin, Walter (1976). 《Principles of mathematical analysis》. International Series in Pure and Applied Mathematics (영어) 3판. McGraw-Hill. ISBN 978-0-07-054235-8. MR 0385023. Zbl 0346.26002. 2014년 10월 6일에 원본 문서에서 보존된 문서. 2014년 10월 6일에 확인함.
- ↑ Beckmann, Petr (1976), A History of Pi, St. Martin's Griffin, ISBN 978-0-312-38185-1
- ↑ 가 나 김흥식, 세상의 모든지식, 서해문집, 2007, ISBN 89-7483-317-4 545-546쪽
- ↑ 과학동아 2006년 7월호, 원주율 π의 수수께끼
- ↑ 장혜원, 청소년을 위한 동양수학사, 두리미디어, 2006, ISBN 89-7715-160-0, 71쪽
- ↑ 나숙자, 친절한 도형 교과서, 부키, 2007, ISBN 89-6051-016-5, 243쪽
- ↑ Kaye, R.W.. "Archimedean ordered fields" Archived 2009년 3월 16일 - 웨이백 머신. web.mat.bham.ac.uk. Retrieved 2009-11-07.
- ↑ 장혜원, 청소년을 위한 동양수학사, 두리미디어, 2006, ISBN 89-7715-160-0, 70-73쪽
- ↑ 위안싱페이, 장연 역, 중국문명대시야 1, 김영사, 2007, ISBN 89-349-2736-4, 465쪽
- ↑ 중국사학회, 강영매 역, 중국역사박물관 4, 범우사, 2004년, ISBN 89-08-04302-0, 76쪽
- ↑ 가 나 첨단과학과 원주율 Archived 2013년 12월 12일 - 웨이백 머신, 국민일보, 2005-7-11
- ↑ 가 나 사이먼 싱, 박병철 역, 페르마의 마지막 정리, 영림카디널, 2002, ISBN 89-85055-97-6 74-75쪽
- ↑ 日, 쓰쿠바 대학 세계 신기록 원주율 자리수 계산, JPNews, 2009-8-18
- ↑ 円周率の計算けた数で世界記録を樹立 Archived 2012년 6월 28일 - 웨이백 머신, 쓰쿠바 대학 홈페이지 (일본어)
- ↑ 파이(π), 2조7천억 자리까지 계산 Archived 2012년 12월 9일 - 웨이백 머신, 사이언스타임즈, 2010-1-19
- ↑ 日회사원, 원주율 소수점 이하 5조 자리까지 계산 성공 :: 네이버 뉴스
- ↑ Peter Trüb가 계산한 값 22조 자리 중 첫 1조 자리의 값은 http://pi2e.ch/blog/ 사이트에서 다운로드 받을 수 있다.
- ↑ 김흥식, 세상의 모든지식, 서해문집, 2007, ISBN 89-7483-317-4 547쪽
- ↑ Laczkovich, Miklós (1997), "On Lambert's proof of the irrationality of π", American Mathematical Monthly 104 (5): 439–443, ISSN 0002-9890
- ↑ Zhou, Li; Markov, Lubomir (2010), "Recurrent Proofs of the Irrationality of Certain Trigonometric Values", American Mathematical Monthly 117 (4): 360–362
- ↑ 김태성, e 및 π의 초월성과 고등학교에서 초월수 지도 Archived 2012년 11월 7일 - 웨이백 머신, 한국수학교육학회 A 통권 14권 2호, 1976년, 17-22
- ↑ Hilberts Beweis der Transzendenz der Ludolphschen Zahl π Archived 2011년 7월 16일 - 웨이백 머신(독일어)
- ↑ 가 나 장우석, 수학 철학에 미치다, 숨비소리, 2008년, ISBN 89-93265-01-1, 174-178쪽
- ↑ Arndt, J. & Haenel, C. (2001), Pi — Unleashed, Berlin: Springer, p. 3, ISBN 3-540-66572-2.
- ↑ 나카다 노리오, 황소연 역, 피라미드에서 수학을 배우자 (수학의 도레미 3), 이지북, 2001년, ISBN 89-89422-62-0, 160-161쪽
- ↑ Pierre Eymard,Jean Pierre Lafon, The number π, 45p.
- ↑ Opera mathematica ... opera atque studio Francisci à Schooten, Leydensis, ... - P400L17,Variorum de rebus Mathèmaticis Reíponíorum Liber VIII
- ↑ Lennart Berggren,Jonathan M. Borwein,Peter B. Borwein, Pi, a source book
- ↑ Lange, L. J. (May 1999). "An Elegant Continued Fraction for π". The American Mathematical Monthly 106 (5): 456–458. doi:10.2307/2589152
- ↑ Stein, Sherman (2006). 《아르키메데스》. 번역 이우영. 경문사. 145-168쪽. ISBN 89-7282-926-9.
- ↑ 가 나 박은순 (2008). 《쉬운 미분·적분학》. 숭실대학교출판부. ISBN 89-7450-235-6.
- ↑ 존 더비셔, 박병철 역, 《리만 가설》, 승산, ISBN 978-89-88907-88-7, 99-122쪽
- ↑ Proving A Proof Is A Proof « Gödel’s Lost Letter and P=NP
- ↑ Smith, Julius O.. "Euler's Identity", Mathematics of the Discrete Fourier Transform (DFT). W3K Publishing. 0-9745607-0-7. 2011년 2월 5일에 확인.
- ↑ Gaussian Integral, MathWorld, 2004-10-07 확인
- ↑ Cauchy Distribution, MathWorld, 2007-11-08 확인
- ↑ Probability Function Archived 2011년 8월 15일 - 웨이백 머신, MathWorld, 2007-11-08 확인함
- ↑ Weisstein, Eric W (2005-12-12). "Buffon's Needle Problem". MathWorld. Retrieved 2007-11-10.
- ↑ 문성수, 정설 재료역학, 기전연구사, 2000년, ISBN 89-336-0539-8, 52-53쪽
- ↑ 존 테일러, 강희재 외 역, 현대물리학, 교보문고, 2005, ISBN 89-7085-543-2, 242-244쪽
- ↑ Einstein, Albert (1916). "The Foundation of the General Theory of Relativity" Archived 2006년 8월 29일 - 웨이백 머신 (PDF). Annalen der Physik.
외부 링크[편집]
 위키미디어 공용에 원주율 관련 미디어 분류가 있습니다.
위키미디어 공용에 원주율 관련 미디어 분류가 있습니다.- “산학의 원주율”. 《네이버캐스트》.
- “원주율 π”. 《네이버캐스트》.
- 온라인 원주율 계산기
- (영어) Project Gutenberg E-Text containing a million digits of Pi Archived 2004년 7월 1일 - 웨이백 머신
- (영어) From the Wolfram Mathematics site lots of formulae for π
- (영어) 원주율에 관한 것
- (영어) Peter Trüb가 계산한 원주율 - 소수점 아래 22조 자리까지 계산

































































