연속 함수

위상수학과 해석학에서, 연속 함수(連續函數, 문화어: 련속함수, 영어: continuous function)는 정의역의 점의 "작은 변화"에 대하여, 치역의 값 역시 작게 변화하는 함수이다.

정의

점에서의 연속성

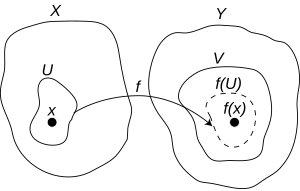
위상 공간 $X$ 및 $Y$ 사이의 함수 $f\colon X\to Y$ 및 점 $x\in X$가 다음 조건을 만족시킨다면, $f$가 점 $x$에서 연속 함수이다(continuous at the point x)라고 한다.

• 임의의 점 $x\in X$ 및 근방 $V\ni f(x)$에 대하여, $f(U)\subseteq V$인 $x$의 근방 $U\ni x$가 존재한다.

위상 공간 $X$ 및 $Y$ 사이의 함수 $f\colon X\to Y$에 대하여, 다음 조건들이 서로 동치이며, 이를 만족시키는 함수를 연속 함수라고 한다.

• 임의의 열린 집합 $U\subseteq Y$에 대하여, 원상 $f^{-1}(Y)\subseteq X$는 열린 집합이다.
• 임의의 닫힌 집합 $C\subseteq Y$에 대하여, 원상 $f^{-1}(C)\subseteq X$는 닫힌 집합이다.
• $f$는 $X$의 모든 점에서 연속 함수이다.
• 임의의 부분 집합 $A\subseteq X$에 대하여, 항상 $f(\operatorname {cl} (A))\subseteq \operatorname {cl} (f(A))$이다. 여기서 $\operatorname {cl}$은 폐포를 일컫는다.

위상 공간 $X$ 및 $Y$ 사이의 함수 $f\colon X\to Y$가 다음 조건을 만족시킨다면, $f$를 점렬 연속 함수(點列連續函數, 영어: sequentially continuous function)라고 한다.

• 임의의 점렬 $x_{i}\in X$ 및 점 $x\in X$에 대하여, 만약 $x_{i}\to x$라면 $f(x_{i})\to f(x)$이다.

좌·우 연속성

어떤 구간 $I\subset \mathbb {R}$ 및 위상 공간 $Y$ 사이의 함수 $f\colon I\to Y$ 및 실수 $r\in I$에 대하여, 다음을 정의하자.

• 만약 $\lim _{x\to r^{+}}f(x)=f(c)$라면, $f$는 $c$에서 우연속 함수(영어: right-continuous function)이다.
• 만약 $\lim _{x\to r^{-}}f(x)=f(c)$라면, $f$는 $c$에서 좌연속 함수(영어: left-continuous function)이다.

성질

연속함수는 위상공간의 몇가지 성질을 보존하기 때문에 매우 유용하다.

• f : X → Y 와 g : Y → Z 가 연속 함수이면 합성 함수 g o f : X → Z 도 연속 함수이다.
• f : X → Y 가 연속 함수이면
  • X 가 콤팩트 공간이라면, f(X) 도 콤팩트 공간이다.
  • X 가 연결 공간이라면, f(X) 도 연결 공간이다.
  • X 가 경로 연결 공간이라면, f(X) 도 경로 연결 공간이다.

임의의 두 위상 공간 $X$, $Y$ 사이의 점렬 연속 함수는 항상 연속 함수이다. 만약 $X$가 제1 가산 공간이라면, $X$와 $Y$ 사이의 함수에 대하여 연속 함수와 점렬 연속 함수가 서로 동치이다.

거리 공간에서의 연속 함수

 엡실론-델타 논법 문서를 참고하십시오.

두 거리 공간 $(X,d_{X})$ 및 $(Y,d_{Y})$ 사이의 함수 $f\colon X\to Y$ 및 점 $x\in X$에 대하여, 다음 두 조건이 서로 동치이다.

• $f\colon X\to Y$는 $x$에서 연속 함수이다.
• 임의의 양의 실수 $\epsilon >0$에 대하여, 다음 조건을 만족시키는 양의 실수 $\delta _{\epsilon }$이 존재한다.
  • 임의의 $x'\in X$에 대하여, 만약 $d_{X}(x,x')<\delta _{\epsilon }$라면, $d_{Y}(f(x),f(x'))<\epsilon$이다.

실수값 연속 함수

임의의 위상 공간 $X$ 위의 두 연속 함수

$f,g\colon X\to \mathbb {R}$

에 대하여, 다음이 성립한다.

• $f+g\colon X\to \mathbb {R}$는 연속 함수이다.
• $fg\colon X\to \mathbb {R}$는 연속 함수이다.
  • 상수 함수는 연속 함수이므로, 만약 $g$가 임의의 실수 $r$라면, $rf\colon X\to \mathbb {R}$는 연속 함수이다.
• 만약 모든 $x\in X$에 대하여 $f(x)\neq 0$이라면, $1/f$는 연속 함수이다.

실수 위의 함수

실수 구간 $I\subset \mathbb {R}$으로부터 위상 공간 $Y$로 가는 함수 $f\colon I\to \mathbb {R}$ 및 임의의 실수 $r\in I$에 대하여, 다음이 성립한다.

• $f$는 $r$에서 좌연속 함수이며 우연속 함수이다.
• $f$는 $r$에서 연속 함수이다.

예

실수선에 표준적인 위상을 정의하였을 때, 다음 함수들은 연속 함수이다.

• 모든 다항식 $\mathbb {R} \to \mathbb {R}$
• 지수 함수 $\exp \colon \mathbb {R} \to \mathbb {R}$
• 사인 $\sin \colon \mathbb {R} \to \mathbb {R}$
• 코사인 $\cos \colon \mathbb {R} \to \mathbb {R}$
• 절댓값 $|\cdot |\colon \mathbb {R} \to \mathbb {R}$

다음 함수는 연속 함수가 아니다.

• 부호 함수 $\operatorname {sgn} \colon x\mapsto {\begin{cases}1&x>0\\0&x=0\\-1&x<0\end{cases}}$

참고 문헌

• Munkres, James R. (2000). 《Topology》 2판. Prentice Hall. ISBN 978-013181629-9. MR 0464128. Zbl 0951.54001.  CS1 관리 - 추가 문구 (링크)

바깥 고리

• “Continuous function”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4. 
• “Continuous mapping”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4. 
• Weisstein, Eric Wolfgang. “Continuous function”. 《Wolfram MathWorld》 (영어). Wolfram Research. 
• Weisstein, Eric Wolfgang. “Continuous map”. 《Wolfram MathWorld》 (영어). Wolfram Research. 
• Weisstein, Eric Wolfgang. “Piecewise continuous”. 《Wolfram MathWorld》 (영어). Wolfram Research. 

같이 보기

• 반연속성
• 불연속점의 분류
• 균등 연속 함수
• 절대 연속 함수
• 립시츠 연속 함수
• 동등연속
• 유계 작용소