시공간
| 시리즈의 일부 |
| 시공간 |
|---|
 |
| 특수 상대성이론 · 일반 상대성이론 |
물리학에서, 시공간은 공간의 3차원과 시간의 1차원을 한 단일 4차원 연속체로 융합하는 어떤 수학적 모형이다. 시공간 다이어그램은 다른 관찰자들이 어떻게 어디에서 그리고 언제 사건들이 발생하는가를 인식하는지와 같은 상대론적 효과들을 시각화하고 또한 이해하는데에 유용하다.
20세기에 접어들 무렵까지, 우주의 3차원 기하학(위치들, 모양들, 거리들 및 방향들에 관한 그 기술)은 1차원 시간(우주 내에서 언제 사건들이 발생하는가의 측정)과 구별된다고 가정이 있었다. 그렇지만, 로런츠 변환과 특수 상대성이론과 더불어 공간과 시간은 새로운 의미를 갖게 되었다.
1908년에, 헤르만 민코프스키는 시간과 공간의 세 가지 차원을 현재 민코프스키 공간으로 알려진 한 단일 4-차원 연속체로 융합하는 특수 상대성이론에 대한 한 기하학적 해석을 제시했다. 이 해석은 일반 상대성이론에 불가결한 것으로 증명되었으며, 여기에서는 시공간이 질량과 에너지에 의해서 휘어진다.
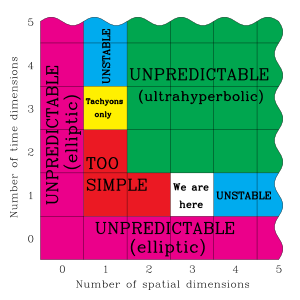
기본들[편집]
정의들[편집]
비상대론적 고전역학은 시간을 공간 전체에 걸쳐 균일하고 공간과 분리된 한 보편적 측정량으로 취급한다. 고전역학은, 관찰자의 운동 상태나 외부의 어떤 것과도 관계없이, 시간이 한 일정한 흐름의 속도로 갖는다고 가정한다.[1] 또한, 그것은 공간이 유클리드라고 가정한다; 그것은 공간이 상식의 기하학을 따른다고 가정한다.[2]
특수 상대성이론의 맥락에서, 시간은 3차원 공간과 분리될 수 없으니, 왜냐하면 한 물체에 대해서 관찰된 시간의 경과하는 속도는 그 관찰자에 대한 물체의 상대 속도에 의존하기 때문이다.[3]:214-217 일반 상대성이론도 또한 중력장들이 그 장 밖의 어떤 관찰자에 의해서 보여질 경우에 어떻게 한 물체를 위한 시간의 흐름을 늦출 수 있는지에 대한 설명을 제공한다.
일반적인 공간에서, 위치는 차원이라고 알려진 세 개의 숫자로 지정된다. 데카르트 좌표계에서는, 이것들은 보통 x, y 및 z라 불린다. 시공간의 한 위치는 한 사건이라고 불리며, 이것은 지정되기 위해 4개의 숫자를 필요로 한다: 즉, 공간에서의 삼차원 위치, 그리고 더하기 시간에서의 위치 (그림 1). 한 사건은 좌표 x, y, z 및 t의 한 집합으로 표시된다.[4] 시공간은 따라서 사차원이다.
폭죽들이나 불꽃들과 같은 사건을 설명하기 위해 대중적인 글에서 사용되는 비유들과 달리, 수학적 사건들은 지속 시간이 영인 지속 지간을 갖으며 또한 시공간에서 한 단일 지점을 나타낸다.[5] 한 폭죽이나 한 불꽃이 튀는 것에 상대적으로 움직이는 것은 가능하지만, 한 관찰자가 한 사건에 대해 상대적으로 움직이는 것은 가능하지 않다.
시공간을 통해 움직이는 한 입자의 경로는 한 사건들의 연속으로 볼 수 있다. 일련의 사건들은 서로 연결되어 한 입자의 시공간을 통한 진행을 나타내는 한 선을 형성할 수 있다. 그 선은 그 입자의 세계선(world line)이라고 불린다.[6]:105
수학적으로 시공간은 한 다양체이며, 말하자면, 이것은 충분히 작은 축척들에서 지구가 평평하게 보이는 것과 같은 방식으로 각 지점 근처에서 국소적으로 "평평하게" 나타난다.[7] 한 척도 인자인 c(일반적으로 광속이라고 부름)는 공간에서 측정된 거리와 시간으로 측정된 거리를 연결한다. 이 척도 인자의 크기(공간에서 거의 300,000km 또는 190,000마일은 시간으로 1초에 해당함)와 시공간의 적절한 모형이 다양체라는 사실은, 보통의 비상대적인 속도와 보통의 인간 규모의 거리에서, 만약 세계가 유클리드적이라면 인간이 관찰할 수 있는 것과 눈에 띄게 다른 것은 거의 없다는 것을 의미한다. 피조 실험(Fizeau experiment)과 마이컬슨-몰리 실험과 같은, 민감한 과학적 측정이 1800년대 중반에 등장하면서야 비로소 유클리드 공간의 암묵적인 가정에 기반한 관측과 예측 사이에 혼란스러운 불일치가 나타나기 시작했다.[8]

특수 상대성이론에서, 한 관찰자는, 대부분의 경우들에 있어서, 대상들이나 사건들의 집합을 측정하는 한 기준 프레임을 의미할 것이다. 이 사용법은 용어의 일반적인 영어 의미와 크게 다르다. 기준 프레임들은 본질적으로 비국소적 구성들이며, 또한 용어의 사용에 따르면, 관찰자가 위치를 가지고 있다고 말하는 것은 이치에 맞지 않는다. 그림 1-1에서, 고려 중인 프레임에 3차원 공간 전체에 걸쳐 무한히 확장되는 이 기준 프레임 내에서 동기화된 조밀한 시계들의 격자가 장착되어 있다고 상상해 보라. 격자 내의 특정 위치는 중요하지 않다. 시계의 격자 구조는 전체 프레임 내에서 발생하는 사건의 시간과 위치를 결정하는 데 사용된다. 관찰자라는 용어는 하나의 기준 관성 프레임과 관련된 시계들의 전체 앙상블을 나타낸다.[9]:17–22 이 이상적인 경우, 공간의 모든 지점에는 연결된 한 시계가 있으므로, 시계는 각 사건을 즉시 등록하며, 한 사건과 그 녹화 사이에는 시간 지연이 없다. 실제 관찰자는, 그렇지만, 빛의 속도로 인해서 신호 방출과 감지 사이에 지연이 있음을 보게 될 것이다. 그 시계들을 동기화하기 위해서, 한 실험에 따르는 데이터 보정(data reduction)에서, 신호가 수신된 시간은 이상적인 시계들의 격자에 의해 기록된 실제 시간을 반영하도록 수정된다.
특수 상대성이론에 관한 많은 책, 특히 오래된 책에서 "관찰자"라는 단어는 보다 일반적인 의미로 사용된다. 어떤 의미가 채택되었는지는 일반적으로 문맥에서 분명하다.
물리학자들은 측정한다 혹은 관찰한다 (사람이 신호 전파 지연을 고려한 후에) 대 그러한 보정들 없이 시각적으로 보는 것을 구별한다. 측정/관찰하는 것 대 보는 것 간의 차이를 이해하지 못하는 것은 상대성의 을 초보 학생들 사이에서 많은 오류의 소스이다.[10]
역사[편집]
1800년대 중반까지, 아라고 반점(Arago spot)의 관찰 및 물 대 공기 중의 광속의 차등적 측정과 같은 다양한 실험은 빛의 미입자 이론(corpuscular theory of light)과 반대되는 빛의 파동 특성을 입증하는 것으로 간주되었다.[11] 파동들의 전파는 한 파동하는 매체의 존재를 필요로 하는 것으로 가정되었다; 광파의 경우, 이것은 한 가상의 루미니퍼러스 에테르로 간주되었다.[노트 1] 그러나그렇지만, 이 가상 매질의 특성을 확립하려는 다양한 시도는 모순된 결과들을 도출했다. 예를 들어, 1851년 프랑스 물리학자 이폴리트 피조에 의해 수행된 피조 실험(Fizeau experiment)은 흐르는 물에서 광속이 공기 중의 광속에 물의 속도를 더한 합보다 물의 굴절률에 의존하는 어떤 양만큼 작다는 것을 증명했다.[12] 다른 문제들 중에서는, 굴절률(파장에 따라 다름)에 대한 이 실험에 의해 암시된 부분적인 에테르-끌림(aether-dragging)의 의존성은 에테르가 서로 다른 색상의 빛에 대해 서로 다른 속도로 동시에 흐른다는 좋지 않은 결론으로 이어졌다.[13] 1887년의 유명한 마이컬슨-몰리 실험(그림 1-2)은 가상의 에테르를 통한 지구의 운동이 빛의 속도에 미치는 차등적 영향을 보여주지 않았으며, 또한 가장 가능성 있는 설명인 완전한 에테르 끌림은, 항성 광행차의 관측과 모순되었다.[8]
1889년 조지 프랜시스 피츠제럴드George Francis FitzGerald[14]와 1892년 헨드릭 로런츠는 독립적으로 고정된 에테르를 통과하는 물질체들이 통과에 의해 물리적으로 영향을 받으며 운동 방향으로 수축하는 것을 설명하는 데 정확히 마이컬슨-몰리 실험의 부정적인 결과에 필요한 양만큼 수축한다고 제안했다. (움직이는 방향의 가로 방향에서는 길이 변화가 일어나지 않는다.)
1904년까지, 로런츠는 그의 이론을 확장하여 아인슈타인이 나중에 도출하게 된 것과 형식적으로 동일한 방정식(즉, 로런츠 변환)과 형식적으로 동일한 방정식에 도달했다[15] 동역학의 한 이론(힘들과 토크들과 그것들의 운동에 미치는 영향의 연구)으로서, 그의 이론은 물질의 물리적 구성 요소들의 실제 물리적 변형들을 가정했다.[16]:163-174 로런츠의 방정식들은 국소 시간이라고 부르는 한 양을 예측했는데, 이것으로 그눈 광행차, 피조 실험 및 기타 현상들을 설명할 수 있었다.
앙리 푸앵카레는 공간과 시간을 시공간으로 결합한 최초의 사람이었다.[17][18]: 73–80, 93–95 그는 1898년에 두 사건들의 동시성은 관습의 문제라고 주장했다.[19][노트 2] 1900년에, 그는 로런츠의 "국소 시간"이 실제로 일정한 광속을 가정한 시계 동기화의 한 명시적인 작동적 정의를 적용함으로써 움직이는 시계들에 의해서 표시되는 것임을 인식했다.[노트 3] 1900년과 1904년에, 그는 그가 상대성 원리라고 부른 것의 타당성을 강조함으로써 에테르에 내재된 탐지 불가능성을 제시했고, 1905/1906년[20] 그는 상대성의 가정에 부합하도록 로런츠의 전자 이론을 수학적으로 완성했다. 로런츠 불변적 중력에 대한 다양한 가설을 논의하면서, 그는 의 다양한 사-벡터, 즉, 4-위치, 4-속도 및 4-힘 를 정의하여 4차원 시공간의 혁신적인 개념을 도입했다.[21][22] 그는 후속 논문들에서 4차원적 형식주의를 추구하지 않았지만, 그렇지만, 이러한 연구의 방식이 "제한된 이익을 위해 큰 고통을 수반하는" 듯하다고 언급하면서, 궁극적으로 "삼차원 언어가 우리 세상을 기술하는 데 가장 적합해 보인다"는 결론을 내렸다. ".[22] 또한, 1909년 후반까지도, 푸앵카레는 로런츠 변환의 동적 해석을 계속 기술했다.[16]:163–174
1905년 알베르트 아인슈타인은 특수 상대성이론을 동역학이 아닌 운동학(힘들에 대한 참조 없이 움직이는 물체들을 연구하는 학문)의 관점에서 분석했다. 그의 결과들은 로런츠와 푸앵카레의 그것들과 수학적으로 동등했다. 그는 전체 이론이 두 가지 가정들을 기반으로 구축될 수 있다는 것을 인식함으로써 이러한 결과를 얻었다: 상대성 원리와 광속 불변의 원리. 그의 연구는 움직이는 시계들 사이의 빛 신호들의 교환, 움직이는 막대들의 길이에 대한 세심한 측정들 및 다른 그러한 예들을 포함하는 생생한 이미지로 가득했다.[23][노트 4][24]
또한, 아인슈타인은 1905년에 일반적 질량-에너지 등가성을 도입함으로써 전자기 질량(electromagnetic mass)-에너지 관계의 이전 시도들을 대체했으며, 이것은 관성 질량과 중력 질량의 등가를 선언한 1907년에의 등가원리의 후속의 공식화에 수단이 되었는데, 이것은 관성 질량과 중력 질량의 등가를 선언한다. 질량-에너지 등가성을 이용하여, 아인슈타인은, 추가로, 한 물체의 중력적 질량이 그 에너지 함량에 비례한다는 것을 보여주었는데, 이것은 일반 상대성이론을 발전시킨 초기 결과들 중 하나였다. 그는 처음에 시공간에 대해 기하학적으로 생각하지 않았던 것으로 보이지만,[3]:219 일반 상대성이론을 더 발전시키면서 아인슈터인은 시공간 형식주의를 완전히 통합했다.
아인슈타인이 1905년에 출판했을 때, 그의 또 다른 경쟁자인 그의 전 수학 교수인 헤르만 민코프스키도 역시 특수 상대성이론의 기본 요소들의 대부분에 도달했다. 막스 보른은 민코프스키의 학생/협력자가 되기 위해 민코프스키와 함께 했던 회의에 대해 자세히 말했다:[25]
나는 쾰른에 가서, 민코프스키를 만났고 또한 1908년 9월 2일에 행해진 그의 유명한 강의 '공간과 시간'을 들었다. [...] 그는 나중에 나에게 아인슈타인이 서로 상대적으로 움직이는 관찰자들의 다른 국소 시간들의 동등성이 표명된 그의 논문을 발표했을 때 그것은 그에게 커다란 충격을 받았다고 말했다; 왜냐하면 그는 독립적으로 동일한 결론에 도달했지만 그러나 그는 먼저 그 모든 훌류함 속에서 수학적 구조를 해결하기를 원했기 때문에 그것들을 출판하지 않았기 때문이다. 그는 결코 우선권 주장을 하지 않았으며 또한 항상 아인슈타인에게 그 위대한 발견에 대한 전적인 몫을 주었다.
민코프스키는 마이컬슨의 파괴적 실험 이후 최소한 1905년 여름 이후 전기역학의 상태에 관심을 가졌는데. 이때 민코프스키와 다비드 힐베르트는 로런츠, 푸앵카레 등의 논문들을 연구하기 위해 당대의 저명한 물리학자들이 참석한 한 고급 세미나를 이끌었다. 민코프스키는 아인슈타인의 작업을 로런츠 작업의 연장선으로 생각했으며, 또한 푸앵카레에 의한 가장 직접적인 영향을 받았다.[26]
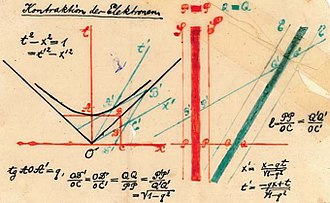
1907년 11월 5일(사망하기 1년 조금 전), 민코프스키는 상대성 원리(Das Relativitätsprinzip)라는 제목으로 괴팅겐 수학 학회에 강의에서 시공간의 기하학적 모형을 소개했다.[노트 5][25] 9월 21일 1908년, 민코프스키는 그의 유명한 강연인 공간과 시간(Raum und Zeit)[27]을 독일 과학자 및 물리학자 협회에서 발표했다. 공간과 시간의 서두는 "이제부터, 공간 단독으로, 그리고 시간 단독으로는 단지 그림자에 불과할 것이며, 또한 이 둘의 어떤 결합만이 독립성을 보존할 것이다"라는 민코프스키의 유명한 언급을 포함한다. 공간과 시간은 시공간 도표(그림 1-4)의 첫 번째 공개 발표를 포함했으며, 또한 불변적 간격의 개념(아래에서 논의됨)을 포함하여, 빛의 속도가 유한하다는 경험적 관찰과 더불어, 특수 상대성이론 전체의 도출 허용한다.[노트 6][27]
시공간 개념과 로런츠 그룹은 구, 쌍곡기하학 또는 등각 기하학(conformal geometry) 및 19세기에 이미 개발된 특정 유형의 변환 그룹들과 밀접하게 연결되어 있으며, 여기에서는 시공간 간격과 유사한 불변 간격이 사용된다.[노트 7][28]:41–42; 39–42[29]:22[30]:3.2.3
아인슈타인은, 그로서는, 처음에는 특수 상대성이론에 대한 민코프스키의 기하학적 해석을 불팔요한 박학함(überflüssige Gelehrsamkeit)으로 간주하며 무시하였다. 그렇지만, 1907년에 시작된 일반 상대성이론에 대한 탐구를 완성하기 위해서는, 상대성이론에 대한 민코프스키 시공간이 주는 기하학적 관점이 불가결함이 입증되었고, 그리고 1916년에, 아인슈타인은 일반 상대성이론으로의 전환을 크게 촉진한 민코프스키에게 대한 자신의 빚을 완전히 인정했다.[16]:151–152 일반 상대성이론의 곡선 시공간과 같은 다른 유형들의 시공간이 있기 때문에, 특수 상대성이론의 시공간은 오늘날 민코프스키 시공간으로 알려져 있다.
특수 상대성이론에서의 시공간[편집]
시공간 간격[편집]
3차원에서, 두 점들 간의 거리 는 피타고라스 정리를 사용하여 정의될 수 있다:
두 명의 보는 사람들이 서로 다른 좌표계들을 사용하여 두 점들의 x, y 및 z 위치를 측정할 수 있지만, 점들 사이의 거리는 둘 다 동일하며(같은 단위를 사용하여 측정한다고 가정하면). 그 거리는 "불변이다".
특수 상대성이론에서는, 그렇지만, 만일 관찰자 중 한 명이 움직이고 있을 때 두 명의 다른 관찰자가 측정하면, 로런츠 수축때문에, 두 점 사이의 거리는 더 이상 동일하지 않다. 두 지점이 공에서 뿐만 아니라 시간에서도 분리되어 있다면 상황은 더욱 복잡해진다. 예를 들어, 만일 한 관찰자가 같은 장소에서 두 개의 이벤트가 발생하지만, 다른 시간에 발생하는 것을 본다면, 첫 번째 관찰자와 관련하여 이동하는 사람은 (자신의 관점에서) 두 사건들이 고정되어 있고, 그 사건의 위치가 멀어지거나 가까워지고 있기 때문에, 두 사건들이 다른 장소에서 발생하는 것으로 볼 수 있다. 따라서, 두 사건들 간의 유효한 "거리"를 측정하려면 어떤 다른 측정을 사용되어야만 한다.[31]:48-50,100-102
사차원 시공간에서, 거리에 대한 유사물은 간격이다. 시간은 한 네 번째 차원으로 들어오지만, 그것은 공간 차원들과는 다르게 취급된다. 민코프스키 공간은 그래서 사차원 유클리드 공간과 중요한 사항들에서 다르다. 공간과 시간을 시공간으로 통합하는 근본적인 이유는 공간과 시간이 별도로 불변하지 않기 때문이니, 말하자면, 적절한 조건에서는, 서로 다른 관찰자들은 두 사건 사이의 시간의 길이(시간 팽창으로 인해) 또는 두 사건들 사이의 거리(길이 수축때문에)에 대해서 동의하지 않을 것이다. 그러나 특수 상대성이론은 공간과 시간의 거리를 결합하는 시공간 간격이라고 부르는 한 새로운 불변량을 제공한다. 어떤 두 사건들 사이의 시간과 거리를 측정하는 모든 관찰자들은 결국 동일한 시공간 간격을 계산하게 될 것이다. 한 관찰자가 와 공간적 거리 에 의해 시간적으로 분리된 두 사건을 측정한다고 가정하라. 그러면 공간에서 거리 와 -좌표에서 에 의해서 로 분리된 두 사건 사이의 시공간 간격 은:[32]:26-28
혹은 삼차원 공간 차원의 경우에는,
상수 인 빛의 속도는 시간 단위(초와 같은)를 공간 단위(미터와 같은)로 변환한다. 간격의 제곱 은 사건가 진행되는 두 개의 분리된 객체들이 있거나 혹은 공간에 있는 단일 객체가 사건들 사이에서 관성적으로 움직이기 때문에 시간적으로 분리되어 있고 공간적으로 분리되어 있는 사건들 A와 B 사이의 분리의 측정값이다. 그 분리 간격은 사건 B와 사건 A를 분리하는 공간 거리를 제곱하고 또한 동일한 시간 간격 에서 광 신호가 이동한 공간 거리의 제곱에서 빼서 도출된다. 만일 사건 분리가 한 광 신호로 인한 것이라면, 이 차이는 사라지고 또한 .
고려된 사건이 서로 극도로 가까울 때, 우리는 쓰기를
다른 한 관성계에서, 말하자면 좌표 로 시공간 간격 는 위과 같은 형식으로 써질 수 있다. 위에. 빛의 속도의 일정성 때문에, 모든 관성계의 빛 사건들은 영 간격인 에 속한다. 인 다른 극소 사건의 경우에는, 임을 증명할 수 있으며, 이는 다시 적분에 의해 로 이어진다.[33]:2 모든 중간 좌표계 사이의 모든 사건 간격의 불변성은 특수 상대성이론의 기본적인 결과들 중 하나이다.
간결성을 위해, 다음 논의의 대부분을 포함하여, 델타들 없이 표현된 간격 표현식을 자주 볼 수 있지만, 일반적으로 는 등을 의미한다는 것이 이해되어야 한다. 우리는 항상 두 사건에 속하는 공간적 또는 시간적 좌표 값들의 차이,'에 대해 관심을 갖고 있으며, 또한 선호되는 원점이 없기 때문에, 단일 좌표 값들은 본질적인 의미를 갖지 않는다.

그 방정식은 와 항들 사이에 마이너스 기호가 있다는 점을 제외하고는 피타고라스 정리와 유사하다. 시공간 간격은 자체가 아니라 수량 이다. 그 이유는 유클리드 기하학의 거리와 달리 민코프스키 시공간의 간격들이 음수일 수 있기 때문이다. 물리학자들은, 음수의 제곱근을 다루기보다, 관습적으로 가 어떤 것의 제곱이 아니라 그 자체로 한 별개의 기호로 간주한다.[3]:217
일반적으로 은 어떤 실수의 값을 가정할 수 있다. 만일 이 양수이면, 그 시공간 간격을 시간꼴로서 참조된다. 어떤 무거운 물체가 가로지르는 공간 거리는 같은 시간 간격 동안 빛이 이동한 거리보다 항상 작기 때문에, 실제 간격은 항상 시간성이다. 만일 가 음수이면 시공간 간격을 공간꼴이라고 말하며, 여기서 시공간 간격은 허수이다. 일 때 시공간 간격은 영과 같다. 다시 말해서, 세계선에서 빛의 속도로 움직이는 두 사건 사이의 시공간 간격은 영이다. 이러한 간격을 빛꼴 또는 널이라고 한다. 먼 별에서 우리 눈에 들어오는 광자는 (우리의 관점에서) 통과하는 데 몇 년이 걸렸음에도 불구하고 나이가 들지 않을 것이다.[31]:48-50
시공간 다이어그램은 일반적으로 한 단일 공간과 한 단일 시간 좌표만으로 그려진다. 그림 2-1은 동일한 사건에서 발생하고 반대 방향으로 진행하는 두 광자들인 A와 B의 세계선들(즉, 시공간의 경로들)을 나타내는 한 시공간 다이아그램을 나타낸다. 또한, C는 광속보다 느린 물체의 세계선을 도해한다. 수직 시간 좌표는 수평 공간 좌표와 동일한 단위(미터)를 갖도록 에 의해 스케일링된다. 광자들은 빛의 속도로 이동하기 때문에, 그것들의 세계선의 기울기는 ±1이다.[31]:23-25 다시 말해서, 광자가 왼쪽이나 오른쪽으로 이동하는 각 미터는 대략 3.3나노초의 시간를 필요로 한다.
상대성 이론에서 사용되는 두 가지 기호 규칙들이 있다:
그리고
이러한 기호 규칙은 계량 부호수 (+−−−) 및 (−+++)와 연관된다. 한 약간의 변형은 시간 좌표를 처음보다 마지막에 배치하는 것이다. 두 규칙들은 둘 다 연구 분야에서 널리 사용된다.[34]
기준 프레임[편집]


서로 다른 기준계들에서 관찰자들이 측정한 시공간 좌표가 서로 어떻게 비교되는지에 대한 통찰력을 얻으려면 한 표준 구성의 프레임로 한 단순화된 설정으로 작업하는 것이 좋다. 조심스럽게, 이것은 도달된 결론들에서 일반성을 잃지 않고 수학의 단순화를 허용한다. 그림 2-2에서는, 두 개의 갈릴레이 기준 프레임들(즉, 기존의 3차원 좌표계들)이 상대적인 움직임으로 표시된다. 프레임 S는 어떤 첫 번째 관찰자 O에 속하고 프레임 S'("S 프라임"으로 발음)는 어떤 두 번째 관찰자 O'에 속한다.
- 프레임 S의 x, y, z축은 프레임 S'의 각 프라임 축과 평행하게 향한다.
- 프레임 S'는 프레임 S에서 측정된 일정한 속도 v로 프레임 S의 x방향으로 이동한다.
- 프레임 S와 S'의 원점들은 프레임 S계에 대해 t = 0이고 프레임 S'에 대해 t′ = 0일 때 일치한다.[6]:107
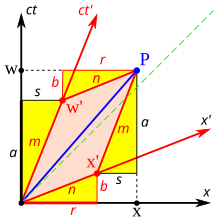
그림 2-3a는 그림 2-2를 한 다른 방향으로 다시 그린다. 그림 2-3b는 관찰자 O의 관점에서 본 시공간 다이어그램을 도해한다. S와 S'는 표준 구성에 있으므로, 프레임 S에서 시간 t = 0, 프레임 S'에서 t′ = 0에서 원점이 일치한다. ct′ 축은 x′ = 0인 프레임 S′계의 사건들을 관통한다. 그러나 x′ = 영이 아닌 점들은 프레임 S의 x 방향으로 속도 v로 이동하므로, ct와 일치하지 않는다. 0이 아닌 다른 시간에 축. 따라서 ct′축은 ct 축에 대해 다음과 같은 각도 θ만큼 기울어진다.
x′축도 x축에 대해 기울어져 있다. 이 기울기의 각도를 결정하기 위해 우리는 한 광 펄스의 세계선의 기울기가 항상 ±1임을 기억한다. 그림 2-3c는 관찰자 O′의 관점에서 본 시공간도를 나타낸다. 사건 P는 x′ = 0, ct′ = -a에서 한 광 펄스의 방출을 나타냉다. 펄스는 광원(사건 Q)에서 거리 a에 위치한 거울에서 반사되고, 또한 x′ = 0, ct′ = a(사건 R)에서 광원으로 돌아간다.
동일한 사건들 P, Q, R은 관찰자 O의 프레임에서 그림 2-3b에 표시된다. 광 경로들은 기울기 = 1 및 -1을 가지므로, △PQR은 45도에서 PQ 및 QR이 모두 x축 및 ct축에 대해 45도인 직각 삼각형을 형성한다. OP = OQ = OR이므로, x′와 x사이의 각도는 θ이여야만 한다.[6]:113-118
정지 프레임은 직각으로 만나는 공간 및 시간 축들을 가지고 있는 반면, 움직이는 프레임은 한 예각으로 만나는 축들로 그려잔다. 그 프레임들은 실제로 동일하다. 비대칭은 시공간 좌표가 데카르트 평면에 매핑될 수 있는 방법의 불가피한 왜곡들로 인한 것이며, 또한 지구의 극 근처의 육지 덩어리의 상대적 크기(그린란드 및 남극 대륙)가 적도 근처의 육지 덩어리에 비해 매우 과장되어 있는 메르카토르 도법 방식보다 보다 더 이상하다고 여겨서는 안된다.
광추[편집]

그림 2-4에서, 사건 O는 시공간 도표의 원점에 있으며, 또한 두 개의 대각선들은 원점 사건에 대해 시공간 간격이 영인 모든 사건을 나타낸다. 이 두 선들은 사건 O의 광추이라고 불리는 것을 형성하는데, 이는 두 번째 공간 차원(그림 2-5)을 추가하면 O에서 정점들을 만나는 두 개의 원뿔들의 모양을 만들기 때문이다. 한 원뿔은 미래(t>0) 로 확장되고, 다른 원뿔은 과거(t<0) 로 확장된다.

한 (이중) 광추는 시공간을 그 정점에 대해서 분리된 영역들로 나눈다. 미래 광추의 내부는 광속으로 공간적 거리를 가로지르는 데 필요한 것보다 더 많은 시간(시간적 거리)만큼 정점에서 분리된 모든 사건들로 구성된다; 이 사건들은 사건 O의 시간꼴 미래를 구성한다. 마찬가지로 시간꼴 과거는 과거 광추의 내부 사건을 포함한다. 그래서 시간꼴 간격 Δct는 Δx보다 커서 시간과 같은 간격들을 양수로 만든다. 광추의 외부 영역은 주어진 시간에 광속으로 건너갈 수 있는 것보다 더 많은 공간만큼 사건 O에서 분리된 사건으로 구성된다. 이러한 사건들은 그림 2-4에서 "다른 곳"으로 표시된 사건 O의 소위 공간꼴 영역으로 구성된다. 광추 자체의 사건은 O에서 빛꼴(또는 널 분리된)이라고 말한다. 시공간 간격의 불변성 때문에, 모든 관찰자들은 주어진 사건에 동일한 광추를 할당할 것이고, 또한 따라서 이러한 시공간의 분할에 동의할 것이다.[3]:220
광추는 인과관계의 개념 내에서 필수적인 역할을 한다. 광속보다 빠르지 않은 신호는 O의 위치와 시간에서 D의 위치와 시간으로 이동할 수 있다(그림 2-4). 따라서 사건 O가 사건 D에 한 인과적 영향을 미칠 수 있다. 미래의 광추는 O에 의해 인과적으로 영향을 받을 수 있는 모든 사건들을 포함한다. 마찬가지로, 광속보다 빠르지 않은 신호는 A의 위치와 시간으로부터 O의 위치와 시간으로 이동한다. 과거의 광추에는 O에 인과적 영향을 미칠 수 있는 모든 사건들을 포함한다. 대조적으로, 신호가 빛의 속도보다 빠르게 이동할 수 없다고 가정하면, 사건, 공간꼴 영역(다른 곳)에서 어떤 사건 즉, 예를 들어 B 또는 C는, 사건 O에 영향을 줄 수 없으며, 또는 이러한 신호를 사용하는 사건 O에 의해 영향을 받을 수도 없다. 이 가정 하에서 사건 O와 광추의 공간꼴 영역의 사건 사이의 어떤 인과 관계도 배제된다.[35]
동시성의 상대성[편집]

모든 관찰자들은 어떤 주어진 사건에 대해서, 주어진 사건의 미래 광추내의 한 사건이 주어진 사건 후에 발생한다는 데 동의한다. 마찬가지로, 어떤 주어진 사건에 대해서, 주어진 사건의 과거 광추 내의 한 사건은 주어진 사건보다 전에 발생한다. 시간꼴-분리된 사건들에 대해 관찰된 전후 관계는 관찰자의 기준 프레임, 즉 관찰자가 어떻게 움직여도 상관없다. 공간꼴-분리된 사건의 경우는 상황이 상당히 다르다. 그림 2-4는 v = 0에서 움직이는 관찰자의 기준 프레임에서 그린 것이다. 이 기준 프레임로부터, 사건 C는 사건 O 후에 발생하는 것으로 관찰되고, 또한 사건 B는 사건 O 전에 발생하는 것으로 관찰된다. 다른 기준 프레임에서 이러한 비인과적인 사건들의 순서는 역전될 수 있다. 특히, 만일 한 특정 기준 프레임에서 두 개의 사건이 동시에 발생하는 경우 필연적으로 공간꼴 간격에 의하여 분리되므로 비인과적으로 관련된다는 점을 주목한다. 동시성이 절대적이지 않고, 관찰자의 기준 프레임에 의존한다는 관찰은 동시성의 상대성이라고 불린다.[36]
그림 2-6은 동시성의 상대성 분석에서 시공간의 다이어그램을 사용하는 것을 보여준다. 시공간에서의 사건들은 불변하지만, 좌표계들은 그림 2-3에 대해 위에서 설명한 대로 변환한다. 세 가지 사건들 (A, B, C)는 v = 0으로 움직이는 관찰자의 기준 프레임에서 동시에 발생한다. v = 0.3c로 움직이는 관찰자의 기준계로부터 사건들은 C, B, A 순서로 발생하는 것으로 보인다. v = −0.5c로 움직이는 관찰자의 기준계로부터 사건들은 A, B, C의 순서로 발생하는 것으로 보인다. 흰색 선은 관찰자의 과거에서 현재 시점으로 이동하는 한 동시성의 평면을 나타낸다. 관찰자의 미래, 거기에 있는 사건을 강조 표시한다. 회색 영역은 관찰자의 광추이고, 이것은 불변함을 유지한다.
만일 측정되는 사건들이 관찰자에게 동시적에 발생했다면 한 공간꼴 시공간 간격은 한 관찰자가 측정하려는 것과 동일한 거리를 제공한다. 공간꼴 시공간 간격은 따라서 고유 거리, 즉 실제 거리 = 의 측정값을 제공한다. 마찬가지로, 시간꼴 시공간 간격은 주어진 세계선을 따라 움직이는 한 시계의 누적 똑딱거림에 의해서 표시되는 것과 동일한 시간 측정값을 제공한다. 한 시간꼴 시공간 간격은 따라서 고유 시간 = 의 한 측정값을 제공한다.[3]:220–221
불변 쌍곡선[편집]

유클리드 공간(공간 차원만 있음)에서 일부 점에서 등거리(유클리드 계량 사용)의 점 집합은 원(2차원) 또는 구(3차원)를 형성한다. (1+1)차원의 민코프스키 시공간(하나의 시간적 차원과 하나의 공간적 차원을 가짐)에서 원점에서 일정한 시공간 간격(민코프스키 계량 사용)에 있는 점은 두 방정식으로 주어진 곡선을 형성한다
이것은 어떤 양의 실수 상수 와 함께 한다. 이 방정식들은x-ct 시공간 도표에서 쌍곡선들의 두 모임들을 설명하는데, 이것들은 불변 쌍곡선들이라 불린다.
그림 2-7a에서, 각 자홍색 쌍곡선들은 원점으로부터 일부의 고정된 공간꼴 분리가 있는 모든 사건들을 연결하고, 반면에 녹색 쌍곡선들은 동일한 시간꼴 분리의 사건들을 연결한다.
x축을 가로지르는 자홍색 쌍곡선은 시간꼴 곡선들이고, 이러한 쌍곡선들은 시공간의 (지속적으로 가속하는) 입자들이 통과할 수 있는 실제 경로들을 나타낸다: 하나의 쌍곡선에 있는 어떤 두 사건들 사이에는 인과관계가 가능한데, 이는 모든 할선들에 대한 기울기-필요한 속도를 나타내는-의 역수가 c보다 작기 때문이다. 반면에, ct축을 가로지르는 녹색 쌍곡선은 이 쌍곡선을 따라 있는 모든 간격이 공간꼴 간격이기 때문에 공간꼴 곡선이다: 이 쌍곡선들 중 하나에 있는 두 점들 사이에는 아무런 인과관계가 가능하지 않다, 왜냐하면 모든 할선들이 c보다 큰 속도들을 나타내기 때문이다.
그림 2-7b는 (1+2)차원적 민코프스키 시공간(1개의 시간적 차원과 2개의 공간적 차원)에서 해당 쌍곡면들의 상황을 반영한다. 원점으로부터 공간꼴 간격들에 의한 변위된 불변 쌍곡선들은 한 장의 쌍곡면을 생성하고, 반면에 원점으로부터 시간꼴 간격만큼 변위된 불변 쌍곡선들은 두 장의 쌍곡면을 생성한다.
원점에 대해 영의 시공간 간격을 형성하는 사건들에 의해 확립된 공간꼴 쌍곡면과 시간꼴 쌍곡면 사이의 (1+2)차원 경계는, 쌍곡면을 광추로 퇴화시켜 구성된다. (1+1)차원에서 쌍곡선들은 그림 2-7a에 표시된 두 개의 회색 45°선들로 퇴화된다.
시간 팽창과 길이 수축[편집]
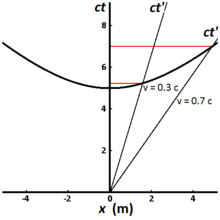
그림 2-8은 5미터(약 1.67 × 10-8초)의 고유 시간에 원점으로부터 도달할 수 있는 모든 사건들에 대한 불변 쌍곡선을 도해한다. 다른 세계 선들은 다른 속도들로 움직이는 시계들을 나타낸다. 관찰자에 대해 정지해 있는 시계는 수직인 한 세계선을 가지며, 관찰자에 의해 측정된 경과 시간은 고유 시간과 동일하다. 0.3c로 이동하는 한 시계의 경우에는 관찰자에 의해 측정된 경과 시간은 5.24미터(1.75 × 10-8s)이고, 반면에 0.7c로 이동하는 시계의 경우 관찰자에 의해 측정된 경과 시간은 7.00미터(2.34 × 10-8초)이다. 이것은 시간 팽창으로 알려진 현상을 도해한다. 더 빨리 이동하는 시계들은 동일한 양의 고유 시간을 똑딱거리는 데 (그 관찰자 프레임에서) 더 오래 걸리며, 또한 시간 팽창이 없는 경우보다 그 고유 시간 내에서 x축을 따라 더 멀리 이동한다.[3]:220–221 다른 관성 기준계에서 두 관찰자들이 시간 팽창을 측정하는 것은 상호적이다. 만일 관찰자 O가 자신의 프레임에서 관찰자 O'의 시계가 느리게 실행되는 것으로 측정하면, 관찰자 O'도 차례로 관찰자 O의 시계가 느리게 실행되는 것으로 측정할 것이다.

길이 수축(length contraction)은, 시간 팽창과 마찬가지로, 동시성의 상대성이론의 한 표명이다. 길이를 측정하려면 한 사람의 기준계에서 동시에 발생하는 두 사건들 사이의 시공간 간격을 측정해야 한다. 그러나 한 기준계에서 동시적인 사건들은, 일반적으로, 다른 기준계들에서는 동시적이지 않다.
그림 2-9는 x축을 따라 0.5c로 이동하는 1m 막대의 운동을 보여준다. 파란색 밴드의 가장자리는 막대의 두 끝점에 대한 세계선을 나타낸다. 불변 쌍곡선은 1m의 공간 간격으로 원점에서 분리된 사건을 나타다. t′ = 0 일 때 측정된 끝점 O와 B는 S′프레임에서 동시 사건이다. 그러나 S프레임의 관찰자에게 사건 O와 B는 동시적이지 않다. 길이를 측정하기 위해서, S프레임의 관찰자는 그 세계선들을 따라 x 축에 투영된 막대의 끝점을 측정한다. x축에 투영된 막대의 세계 쉬트의 투영은 단축된 길이 OC를 산출한다.[6]:125
(도해되지 않은) A를 지나는 수직선을 그려서 x′축 과 교차하면, 관찰자 O의 관점에서 OB가 축소되더라도, 관찰자 O′의 관점에서 OA도 마찬가지로 축소됨을 알 수 있다. 각 관찰자가 상대방들의 시계들이 느리게 움직이는 것으로 측정하는 것과 같은 방식으로, 각 관찰자는 상대방 들의 눈금자들이 수축된 것으로 측정한다.
상호 길이 수축과 관련하여, 그림 2-9는 프라임된 그리고 비프라임된 프레임들은 한 쌍곡선 각도(hyperbolic angle)(유클리드 기하학의 일반 각도와 유사한)에 의해 상호 회전되는 것을 도해한다.[노트 8] 이 회전으로 인해, 비프라임된 x 축에의 한 프라임된 미터-막대의 투영은 축소되며, 반면에 프라임된 x′-축에의 한 비프라임된 미터-막대의 투영도 마찬가지로 축소된다.
상호 시간 팽창과 쌍둥이 역설[편집]
상호 시간 팽창[편집]
상호 시간 팽창과 길이 수축은 초보자를 본질적으로 자기모순적인 개념들로 인식시키는 경향이 있다. 만일 프레임 S의 한 관찰자가 프레임 S'에서 정지한 시계를 자신의 것보다 느리게 가는 것으로 측정하는 반면에, S'가 S에서 속도 v로 움직이면, 상대성 원리는 프레임 S'에서 -v로 움직이는 프레임 S의 한 관찰자도 마찬가지로 프레임 S계의 시계가 그녀의 것보다 느리게 가는 것을 측정한다. 어떻게 두 시계들이 다른 시계보다 들 다 느리게 갈 수 있는지는 "특수 상대성이론을 이해하는 핵심으로 가는" 한 중요한 질문이다.[3]:198
이 명백한 모순은 필요한 관련 측정들의 다른 설정들을 올바르게 고려하지 않은 데서 비롯된다. 이러한 설정들은 유일한 명백한 모순에 대한 한 일관된 설명을 허용한다. 그것은 두 개의 동일한 시계들의 추상적인 똑딱거림에 관한 것이 아니라, 한 움직이는 시계의 두 똑딱임의 시간적 거리를 한 프레임에서 측정하는 방법에 관한 것이다. 각각의 프레임에서 움직이는 시계의 똑딱거림 사이의 지속 시간을 상호 관찰함에 있어서, 다른 시계들의 세트들이 관련되어야만 한다. 프레임 S에서 움직이는 시계 W'(S'에서는 정지)의 똑딱거림 지속 시간을 측정하기 위해서는, 공간 거리 d를 가진 S의 두 개의 임의의 고정된 지점들에서 정지한 두 개의 추가 동기화된 시계 W1 및 W2를 사용한다.
- 두 개의 사건들은 "두 개의 시계가 동시에 한 장소에 있다"는 조건에 의해서 정의할 수 있으니, 즉, 이 때에는 W'가 각 W1 및 W2를 통과한다. 두 사건들 모두에 대해 배치된 시계들의 두 판독값들이 기록된다. W1과 W2의 두 판독값들의 차이는 S에서 두 사건들의 시간적 거리이고 그것들의 공간적 거리는 d이다. W'의 두 판독값의 차이는 S'의 두 사건들의 시간적 거리이다. S'에서는 이러한 사건들이 시간적으로만 분리되어 있으며, S'에서는 같은 장소에서 발생한다. 이 두 사건들에 걸쳐 있는 시공간 간격의 불변성과 S의 영이 아닌 공간 분리로 인해 S'에서의 시간적 거리는 S에서의 시간적 거리보다 작아야 한다. 움직이는 시계 W'의 판독값은 느리게 가는 시계 W'에 속한다.
반대로, 프레임 S'에서 어떤 움직이는 시계 W의 두 사건의 시간적 거리를 판단하려면(S에서는 정지된) S'에서 정지한 두 개의 시계들이 필요하다.
- 이 비교에서 시계 W는 속도 -v로 움직인다. "한 장소에서 동시에 두 개의 시계들"로 정의된 사건들에 대한 네개의 판독값들을 다시 기록하면 두 사건들의 유사한 시간적 거리들이 생성되는데, 이것들은 이제 S'에서 시간적 및 공간적으로 분리되고 또한 시간적으로만 분리되지만 S에 배치된다. 시공간 간격을 불변으로 유지하려면, S'에서의 사건들의 공간적으로 분리 때문에 S에서의 시간적 거리는 S'에서 보다 작아야 한다: 이제 시계 W는 느리게 가는 것으로 관찰된다.
각각 S 또는 S'에 "움직이는 시계 한 개" 및 "정지한 시계 두 개"가 있는 두 가지 판단에 필요한 기록들은 각각 세 개의 시계들이 있는 두 개의 다른 세트들을 포함한다. 측정들과 관련된 다양한 시계 세트들이 있기 때문에, 만일 한 관찰자가 움직이는 시계를 느리게 측정하면, 다른 관찰자는 자신의 시계를 빠르게 측정하도록 하는 그 측정이 상호적으로 "일관성"이 있어야 할 내재적인 필요는 없다.[3]:198-199
그림 2-10은 민코프스키 다이어그램듷과 함께하는 상호 시간 팽창에 대한 이전 논의를 도해한다. 위쪽 그림은 비프라임된 직사각형 축들과 함께 하는 프레임 S와 또한 "v > 0으로 움직이는" 프레임 S'가 오른쪽으로 기울어진 비스듬한 프라임된 축들로부터 보여진 측정값들을 반영한다; 아래쪽 그림은 프라임된 직교 좌표와 함께 하는 "정지 상태"인 프레임 S'와 또한 왼쪽으로 기울어진 비스듬한 비프라임된 축과 함께 하는 "-v < 0으로 움직이는" 프레임 S를 보여준다.
공간 축(x, x′)에 평행하게 그려진 각 선은 동시성의 선을 나타낸다. 이러한 라인의 모든 사건들은 동일한 시간 값(ct, ct′)을 갖는다. 마찬가지로, 시간축(ct, ct′)에 평행하게 그려진 각 선은 동일한 공간 좌표 값들(x, x′)의 선을 나타낸다.
- 두 그림들 모두에서 사건으로서 원점 O (= O′)를 지정할 수 있는데, 여기서 각각의 "움직이는 시계"는 두 비교들에서 "정지 중인 첫 번째 시계"와 함께 배치된다. 분명히, 이 사건의 경우 두 비교에서 두 시계들 모두의 판독값은 영이다. 그 결과, 움직이는 시계들의 세계선은 오른쪽 ct′축(위 그림, 시계 W')으로 기울어져 있고, 또한 왼쪽 ct축(아래 그림, 시계 W)으로 기울어져 있다. W1 및 W'1의 세계선들은 해당하는 수직 시간 축이다(위 그림의 ct, 아래 그림의 ct′).
- 위의 그림에서 W2의 위치는 Ax > 0으로 간주되므로, 따라서 이 시계의 세계선(그림에는 표시되지 않음)은 A라고 표시된 사건에서 움직이는 시계(ct′축)의 세계선과 교차한다. 여기서 "두 개의 시계는 동시에 한 장소에 있다". 아래 그림에서 W'2 위치는 Cx′ < 0인 것으로 간주되므로, 또한 이 측정에서 움직이는 시계 W는 사건 C에서 W'2를 통과한다.
- 위 그림에서 사건 A(W2의 판독값)의 ct좌표 At 는 B로 표시되고, 따라서 W1과 W2로 측정된 두 사건 사이의 경과 시간을 OB로 제공한다. 비교를 위해, W'로 측정한 시간 간격 OA의 길이는 ct축의 눈금으로 변환되어야만 한다. 이것은 A를 통한 불변 쌍곡선(그림 2-8 참조)에 의해 수행되며, A와 원점으로부터 동일한 시공간 간격을 가진 모든 사건들을 연결한다. 이것은 ct-축에 사건 C를 산출하고, 또한 분명히: OC < OB 이라서, "움직이는" 시계 W'는 느리게 간다.
바로 위 그림에서 상호 시간 팽창을 보여주기 위해 사건 D는 x′ = 0(S에서 시계 W의 위치)에서의 사건으로 구성될 수 있으며, 이는 S에서 C(OC는 OA 와 동일한 시공간 간격을 가진다)와 동시적이다. 이것은 시간 간격 OD가 OA보다 길다는 것을 보여주며, "움직이는" 시계가 느리게 간다는 것을 보여준다.[6]:124
아래 그림에서 프레임 S는 정지된 프레임 S'에서 −v의 속도로 움직이고 있다. 시계 W의 세계선은 ct축(왼쪽으로 기울어진)이고, W'1의 세계선은 세로 ct′축이며, 또한 W'2는 ct′-좌표 D가 있는 사건 C를 통한 수직이다. 사건 C를 통한 불변 쌍곡선은 시간 간격 OC를 OD보다 짧은 OA로 조정한다; 또한 B는 (위 그림의 D와 유사하게) x = 0에서 S의 A와 동시에 구성된다. 결과 OB > OC는 다시 위와 부합한다.
"측정"이라는 단어가 중요하다. 고전 물리학에서 한 관찰자는 한 관찰된 대상에 영향을 줄 수 없지만, 그러나 그 대상의 운동 상태는 관찰자의 대상에 대한 관찰들에 영향을 줄 수 있다.
쌍둥이 역설[편집]
특수 상대성이론에 대한 많은 소개는 일련의 "역설"을 제시함으로써 갈릴레이 상대성이론과 특수 상대성이론의 차이점을 설명한다. 이러한 역설은 사실, 빛의 속도에 필적하는 속도에 익숙하지 않기 때문에 발생하는 잘못된 문제이다. 해결책은 특수 상대성이론의 많은 문제를 해결하고 소위 반직관적 예측에 익숙해지는 것이다. 시공간을 연구하는 기하학적 접근 방식은 현대적인 직관력을 개발하는 가장 좋은 방법 중 하나로 간주된다.[37]
쌍둥이 역설은 일란성 쌍둥이가 고속 로켓을 타고 우주로 여행을 갔다가 집으로 돌아와 지구에 남아 있던 쌍둥이가 더 늙어가는 것을 발견하는 사고 실험이다. 이 결과는 각 쌍둥이가 다른 쌍둥이가 움직이는 것을 관찰하기 때문에 어리둥절해 보이고, 언뜻 보기에는 서로가 덜 늙었다고 생각해야 하는 것처럼 보일 것이다. 쌍둥이 역설은 세 번째 시계에 대한 요구 사항을 피함으로써 위에서 제시된 상호 시간 팽창의 정당성을 회피한다.[3]:207 그럼에도 불구하고, 쌍둥이 역설은 특수 상대성이론의 맥락에서 쉽게 이해되기 때문에 진정한 역설이 아니다.
역설이 존재한다는 인상은 특수 상대성이론에 대한 오해에서 비롯된다. 특수 상대성이론은 모든 기준 프레임들이 동등하다고 선언하지 않고, 관성 프레임들만을 그렇다고 선언한다. 여행 중인 쌍둥이의 프레임은 가속하는 동안에는 관성적이 아니다. 게다가, 쌍둥이 사이의 차이는 관찰할 수 있다. 여행 중인 쌍둥이는 집으로 돌아가기 위해 로켓을 발사해야 하지만 집에 있는 쌍둥이는 그렇지 않다.[38][노트 9]
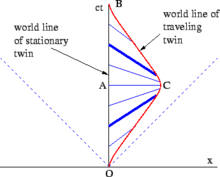
이러한 구별은 쌍둥이의 나이 차이가 발생해야 한다. 그림 2-11의 시공간 도표는 x축을 따라 직선으로 갔다가 즉시 되돌아오는 쌍둥이의 간단한 경우를 나타낸다. 재택 쌍둥이의 입장에서 볼 때 쌍둥이 역설은 전혀 당혹스러울 것이 없다. O에서 C까지 여행하는 쌍둥이의 세계선을 따라 측정한 고유 시간과 C에서 B까지 측정한 고유 시간은 O에서 A에서 B로 측정된 재택 쌍둥이의 고유 시간보다 짧다. 더 복잡한 궤적은 여행 중인 쌍둥이가 경험한 고유 시간의 총량을 계산하기 위해서는 곡선을 따라(즉, 경로 적분) 각 사건 사이의 고유 시간을 적분하여야 한다.[38]
쌍둥이 역설을 여행하는 쌍둥이의 관점에서 분석하면 문제가 발생한다.
집에 있는 쌍둥이를 테렌스Terence로, 여행 중인 쌍둥이를 스텔라Stella로 지정하는 바이스Weiss의 명명법이 이후에 사용된다.[38]
스텔라는 관성 프레임에 있지 않다. 이 사실을 감안할 때, 쌍둥이 역설의 완전한 해결은 일반 상대성이론을 필요로 한다고 잘못 언급되는 경우가 있다.[38]
순수한 SR(특수 상대성) 분석은 다음과 같다. 스텔라의 정지 프레임에서 분석하면 그녀는 전체 여행 동안 움직이지 않는다. 그녀가 선회를 위해 로켓을 발사할 때, 그녀는 중력과 유사한 유사 힘을 경험한다.[38] 그림 2-6 및 2-11은 동시성의 선(평면) 개념을 보여준다: 관찰자의 x-축(xy-평면)에 평행한 선은 관찰자 계에서 동시에 발생하는 일련의 사건 나타낸다. 그림 2-11에서 파란색 선은 스텔라의 관점에서 그녀의 세계선에서 사건과 동시에 발생하는 테렌스 세계선에서 사건을 연결한다. (테렌스는 동시에 일련의 수평선을 관찰할 것이다.) 스텔라의 여정의 출발 및 복귀 구간 모두에서 그녀는 테렌스의 시계가 자신보다 느리게 작동하는 것으로 측정한다. 그러나 방향 전환을 하는 동안(즉, 그림에서 굵은 파란색 선 사이), 스텔라가 동시성으로 간주하는 테렌스의 세계선에서 사건의 빠른 건너뛰기에 해당하는 동시성 선의 각도에서 이동이 발생한다. 따라서 여행이 끝나면 스텔라는 테렌스가 자신보다 더 늙었다는 것을 알게 된다.[38]
쌍둥이 역설을 분석하는 데 일반 상대성이론이 필요하지는 않지만 일반 상대성이론의 등가 원리를 적용하면 주제에 대한 추가 통찰력을 얻을 수 있다. 스텔라는 관성 프레임에서 고정되어 있지 않다. 스텔라의 정지 프레임으로 분석하면 그녀는 전체 여행 동안에 움직이지 않는다. 그녀가 코스팅(coasting)할 때 그녀의 정지 프레임은 관성적이며 테렌스의 시계는 느리게 작동하는 것처럼 보인다. 그러나 그녀가 방향 전환을 위해 로켓을 시동할 때, 그녀의 정지 프레임은 한 가속된 프레임이고 또한 그녀는 마치 중력장에 있는 것처럼 그녀를 밀어내는 어떤 힘을 경험한다. 테렌스는 그 장에서 높은 위치에 있는 것처럼 보일 것이며 또한 중력 시간 팽창으로 인해, 그의 시계가 빠르게 작동하는 것처럼 보일 것이므로, 최종 결과는 그들이 다시 만났을 때 테렌스는 스텔라보다 더 나이들게 될 것이다.[38] 중력 시간 팽창을 예측하는 이론적 주장들은 일반 상대성이론에만 국한되지 않는다. 만일, 뉴턴의 이론을 포함하여, 등가 원리를 존중한다면 모든 중력의 이론들은 중력 시간 팽창을 예측할 것이다.[3]:16
중력[편집]
이 입문 섹션은 설명하기 가장 쉬운 특수 상대성이론의 시공간에 초점을 맞췄다. 민코프스키 시공간은 평평하고 중력을 고려하지 않고 전체적으로 균일하며 그 안에서 일어나는 사건에 대한 정적 배경에 불과하다. 중력의 존재는 시공간의 기술을 매우 복잡하게 만든다. 일반 상대성이론에서 시공간은 더 이상 정적인 배경이 아니라 그 안에 포함된 물리적 시스템과 능동적으로 상호 작용한다. 물질이 있는 상태에서 시공간 곡선은 파동을 전파하고 빛을 구부리며 기타 여러 현상을 나타낼 수 있다.[3]:221 이러한 현상 중 몇 가지에 대해서는 이 문서의 나중 섹션들에서 설명한다.
시공간의 기초 수학[편집]
갈릴레이 변환[편집]
한 기본 목표는 상대 운동에서 관찰자가 수행한 측정을 비교할 수 있도록 하는 것이다. 만일 프레임 S에 사건의 시간 및 공간 좌표를 측정한 관찰자 O가 있다면, 이 사건에 3개의 데카르트 좌표와 동기화된 시계 (x, y, z, t)의 격자에서 측정된 시간을 할당한다(그림 1-1 참조). 다른 프레임 S'의 두 번째 관찰자 O'는 좌표계와 동기화된 시계 격자 (x′, y′, z′, t′)에서 동일한 사건을 측정한다. 관성 프레임에서는 어느 관찰자도 가속되지 않으며 간단한 방정식 세트를 통해 좌표 (x, y, z, t)를 (x′, y′, z′, t′)에 연관시킬 수 있다. 평행한 (x, y, z) 좌표와 정렬되고 t′ = 0일 때 t = 0인 경우를 의미하는 두 좌표계가 표준 구성에 있으면, 좌표 변환은 다음과 같다.[39][40]
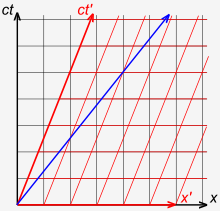
그림 3-1은 뉴턴의 이론에서는, 시간은 보편적이지만, 빛의 속도는 그렇지 않다는 것을 보여준다.[41]:36-37 다음과 같은 사고 실험을 고려하라: 빨간색 화살표는 플랫폼을 기준으로 0.4c로 이동하는 열차를 나타낸다. 열차 안에서 승객이 열차의 계 안에서 0.4c의 속도로 총알을 쏜다. 파란색 화살표는 기차 선로에 서 있는 사람이 0.8c로 이동하는 것으로 탄환을 측정한다는 것을 보여준다. 이것은 우리의 순진한 기대와 일치한다.
보다 일반적으로, 프레임 S'가 프레임 S에 대해 속도 v로 움직이고 있다고 가정하면, 프레임 S' 내에서 관찰자 O'는 속도 u′로 움직이는 물체를 측정한다. x = ut, x′ = x − vt, t = t′이므로 프레임 S에 대한 속도 u는 다음과 같이 쓸 수 있다. x′ = ut − vt = (u − v)t = (u − v)t′. 이것은 u′ = x′/t′로 이어지며 궁극적으로
- 또는
이것은 상식적인 속도들의 덧셈에 대한 갈릴레이 법칙이다.
속도들의 상대론적 구성[편집]

속도들의 구성은 상대론적 시공간에서 상당히 다르다. 방정식의 복잡성을 조금 줄이기 위해 빛에 대한 물체의 속도 비율에 대한 다음의 일반적 축약법을 도입하여,
그림 3-2a는 v/c = β = s/a로 주어진 어떤 속도로 전진하는 한 빨간색 기차를 보여준다. 기차의 프라임된 프레임에서 한 승객은 u′/c = β′ = n/m로 주어진 어떤 속도로 총알을 쏘는데. 여기서 그 거리는 검은색 x축에 평행하지 않고 빨간색 x′축에 평행한 한 선을 따라 측정된다. 파란색 화살표로 표시된 플랫폼에 대한 총알의 합성 속도 u는 얼마일까? 그림 3-2b 참조하면:
- 플랫폼으로부터, 총알의 합성 속도는 u = c(s + r)/(a + b)로 주어진다.
- 두 개의 노란색 삼각형들은 공통 각도 α를 공유하는 직삼각형이기 때문에 닮음 꼴이다. 그 비율 s/a = v/c = β이다.
- 두 개의 노란색 삼각형들의 대응하는 변의 비율은 일정하므로, r/a = b/s = n/m = β′. 따라서 b = u′s/c}} 그리고 r = u′a/c.
- 속도들 덧셈에 대한 아인슈타인의 공식을 산출하기 위해서 b 및 r에 대한 표현식을 1단계의 u에 대한 표현식에 대입하라.[41]:42–48
위에 제시된 속도들의 덧셈을 위한 상대론적 공식은 몇 가지 중요한 특징들을 보여준다:
- 만일 u′ 및 v가 모두 빛의 속도에 비해 매우 작으면, 곱셈 vu′/c2는 사라지게 작아지고, 또한 전체 결과는 속도들의 덧셈에 대한 갈릴레이 공식(뉴턴 공식)과 구별할 수 없게 된다: u = u′ + v. 갈릴레이 공식은 낮은 속도들에 적용되는 상대론적 공식의 한 특수한 경우이다.
- 만일 u′가 c와 같게 설정되면, 수식은 v의 시작 값에 관계없이 u = c를 산출한다. 빛의 속도는 방출하는 소스에 대한 그들의 상대적인 움직임에 관계없이 모든 관찰자에게 동일하다.[41]:49
시간 팽창과 길이 수축 재검토[편집]

시간 팽창과 길이 수축에 대한 정량적 표현을 얻는 것은 간단하다. 그림 3-3은 두개의 이전 애니메이션들에서 가져온 개별적 프레임들을 포함하는 한 합성 이미지이며, 이 섹션의 목적을 위해 단순화되고 레이블이 다시 지정되었다.
방정식들의 복잡성을 약간 줄이기 위해서, ct에 대한 다양한 축약 표기법이 있다.
- 그리고 는 일반적이다.
- 또한 관례 의 매우 자주 사용됨을 본다.

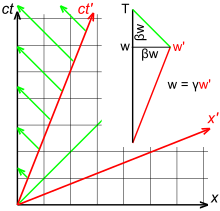
그림 3-3a에서 선분들 'OA'와 'OK'는 동일한 시공간 간격들을 나타낸다. 시간 팽창은 OB/OK 비율로써 표시된다. 불변 쌍곡선의 방정식은 w = √x2 + k2를 가지며 여기서 k = OK 이고, 움직이는 입자의 세계선을 나타내는 빨간색 선은 방정식 w = x/β = xc/v를 가진다. 약간의 대수적 조작은 을 산출한다.
제곱근 기호를 포함하는 표현은 상대성 이론에서 매우 자주 등장하며, 또한 그 표현 위에 하나를 로런츠 인자라고 불리며 그리스 문자 감마 로 표시된다:[42]
만일 v가 c보다 크거나 같으면, 에 대한 표현은 물리적으로 의미가 없어졔서, c가 자연에서 가능한 최대 속도임을 의미한다. 영보다 큰 모든 v의 경우, 로런츠 인자는 1보다 크지만, 곡선의 모양은 저속에서는 로런츠 인자가 1에 극도로 가깝다.
그림 3-3b에서 선분 'OA'와 'OK'는 동일한 시공간을 나타낸다. 길이 수축은 OB/OK 비율로 표시된다. 불변 쌍곡선은 방정식 x = √w2 + k2를 갖으며, 여기서 k = OK, 그리고 움직이는 막대 끝점의 세계선을 나타내는 파란색 띠의 가장자리는 기울기 1/β = c/v를 갖는다. 사건 A는 좌표 (x, w) = (γk, γβk)를 갖즌다. A와 B를 지나는 접선은 방정식 w = (x − OB)/β를 가지므로, 우리는 γβk = (γk − OB)/β 및 다음을 갖는다.
로런츠 변환들[편집]
갈릴레이 변환들과 그에 따른 속도들의 덧셈의 상식적인 법칙은 비행기, 자동차 및 공으로 구성된 일반적인 저속 세계에서 잘 작동한다. 그러나 1800년대 중반부터, 민감한 과학 기기가 일반적인 속도 법칙과 맞지 않는 이상 현상들을 발견하기 시작했다.
로런츠 변환들은 특수 상대성이론에서 사건의 좌표를 한 계에서 다른 계으로 변환하는 데 사용된다.
로런츠 인자는 로런츠 변환에 나타난다.
역 로런츠 변환은:
v ≪ c이고 그리고 x가 충분히 작을 때, v2/c2와 vx/c2 항이 영에 접근하고, 그러면 로런츠 변환들은 갈릴레이 변환들에 근사치이다.
등은 대부분 종종 실제로는 등을 의미한다. 로런츠 변환은 간결함을 위해 델타들 없이 작성되지만, x는 Δx 등을 의미한다. 우리는, 일반적으로, 항상 사건 간의 공간과 시간 '차이'에 관심을 갖는다.
한 집합의 변환들을 일반 로런츠 변환들이라고 부르고 다른 하나는 역변환들이라고 부르는 것은 프레임들 간에 본질적인 차이가 없기 때문에 오해의 소지가 있다. 다른 저자들은 하나 또는 다른 변환들의 세트를 "역" 집합라고 부른다. S 프레임은 S'에 대해서만 앞으로 또는 뒤로 이동할 수 있기 때문에 순방향 및 역변환은 서로 자명한 관련이 있다. 따라서 방정식들을 뒤집는 것은 단순히 프라임된 변수들과 비프라임돤 변수들을 전환하고 v를 -v로 바꾸는 것을 수반한다.[43]:71–79.
예: 테렌스와 스텔라는 한 지구에서-화성까지 우주 경주를 하고 있다. 테렌스는 그 출발선에 있는 한 심판원이고 스텔라는 한 참가자이다. t = t′ = 0 시간에 스텔라의 우주선은 순간적으로 0.5 c의 속도로 가속된다. 지구에서 화성까지의 거리는 300광초(약 90.0×106 km)이다. 테렌스는 t = 600.00 s에 결승선 시계를 통과하는 스텔라를 관찰한다. 그러나 스텔라는 우주선 크로노미터(정밀 시계)의 시간이 임을 관찰한다. 그녀가 결승선을 통과할 때 출발선과 결승선 사이의 거리를, 자신의 프레임에서 측정했을 때, 259.81광초(약 77.9×106 km)로 계산한다.
로런츠 변환들을 유도하기[편집]
1905년 아인슈타인의 독창적인 작업 이후로 수십 가지의 로런츠 변환의 유도(derivations of the Lorentz transformations)들이 있었으며, 각각은 특정한 초점을 가지고 있다. 아인슈타인의 유도는 빛의 속도의 불변성을 기반으로 했지만, 출발점으로 작용할 수 있는 다른 물리적 원리들이 있다. 궁극적으로, 이러한 대안적 출발점들은 밑에 있는 국소성의 원리의 다른 표현으로 간주될 수 있으며, 이것은 하나의 입자가 다른 입자에 미치는 영향이 순간적으로 전달될 수 없다는 것을 진술한다.[44]
여기에 제공되고 또한 그림 3-5에 설명된 유도는 바이스Bais가 제시한 것을 기반으로 하며[41]:64–66 또한 속도들의 상대론적 구성, 시간 팽창 및 길이 수축 섹션들로부터의 이전 결과들을 사용한다. 사건 P는 검은색 "정지 시스템"의 좌표 (w, x)와 속도 매개변수 β = v/c로 움직이는 빨간색 프레임의 좌표 (w′, x′)를 가진디. w′ 및 x′를 w 및 x(또는 그 반대로)로 결정하려면 먼저 '역' 로런츠 변환을 유도한는 것ㄹ이 더 쉽다..
- 가로 방향으로는 길이 확장/수축이 있을 수 없으며, y′는 y와 같아야 하고 또한 z′는 z와 같아야 한다. 그렇지 않으면 빠르게 움직이는 1m 공이 1m 원형 구멍을 통과할 수 있는지는 관찰자에 따라 다르다. 상대성 이론의 첫 번째 가정은 모든 관성 프레임들은 동일하며 가로 확장/수축은 이 법칙을 위반한다는 것이다.[43]:27–28
- 그림에서, w = a + b 또한 x = r + s
- 닮은꼴 삼각형들을 사용한 이전 결과에서 s/a = b/r = v /c = β.
- 시간 팽창 때문에, a = γw′
- 방정식 (4)를 s/a = β 에 대입하면 s = γw′β를 산출한다.
- 길이 수축 및 닮은꼴 삼각형들은 r = γx′ 및 b = βr = βγx′를 제공한다.
- s, a, r 및 b 에 대한 표현식을 2단계의 방정식에 대입하면 즉시 다음이 산출된다
위의 방정식은 역 로런츠 변환의 t와 x 방정식들에 대한 대안적 표현들이며, w를 ct, w′를 ct′, β를 v/c로 대입함으로써 알 수 있다. 역 변환으로부터, t′와 x′에 대해 풀면 순방향 변환 방정식들이 유도될 수 있다.
로런츠 변환들의 선형성[편집]
로런츠 변환에는 선형성이라는 수학적 속성이 있는데, 이는 x′와 t′는 x와 t의 선형 결합으로 얻어지며, 더 높은 거듭제곱이 포함되지 않기 때문이다. 변환의 선형성은 유도에서 암묵적으로 가정된 시공간의 기본 속성, 즉 관성 기준 프레임의 속성이 위치 및 시간에 독립적이라는 것을 반영한다. 중력이 없으면, 시공간은 어디에서나 동일하게 보인다.[41]:67 모든 관성 관찰자는 가속 운동과 비가속 운동을 구성하는 것에 동의할 것이다.[43]:72–73 한 관찰자는 자신의 공간 및 공간 측정을 사용할 수 있지만, 그러나 절대적인 것은 아무것도 없다. 다른 관찰자의 규약도 마찬가지이다.[3]:190
선형성의 결과는 만일 두 개의 로런츠 변환이 순차적으로 적용되면, 그 결과도 한 로런츠 변환이 된다는 것이다.
예: 테렌스는 0.500c에서 스텔라가 자신에게서 멀어지는 것을 관찰하고, 또한 β = 0.500인 로런츠 변환을 사용하여 스텔라의 측정을 자신의 측정과 관련시킬 수 있다. 그녀의 프레임에서, 스텔라는 0.250c에서 그녀에게서 멀어지는 우르슬라를 관찰하고 β = 0.250인 로런츠 변환을 사용하여 우르술라의 측정값을 자신의 측정값과 연결할 수 있다. 변환들의 선형성과 속도들의 상대론적 구성 때문에 테렌스는 β = 0.666인 로런츠 변환을 사용하여 우르술라의 측정값을 자신의 측정값과 연결할 수 있다.
도플러 효과[편집]
도플러 효과는 상대적 운동에서 수신기와 소스에 대한 파동의 주파수 또는 파장 변화이다. 간단히는, 여기에서 두 가지 기본 시나리오를 고려한다: (1) 소스 및 수신기의 동작이 이들을 연결하는 선을 정확히 따르고(종방향 도플러 효과), 또한 (2) 동작이 해당 선에 직각이다(횡방향 도플러 효과(transverse Doppler effect)). 우리는 그들이 중간 각도를 따라 움직이는 시나리오는 무시한다.
종방향 도플러 효과[편집]
고전적인 도플러 분석은 음파 또는 물결과 같은 한 매질에서 전파되고 서로를 향해 또는 멀어지는 소스와 수신기 사이에서 전송되는 파동을 다루며, 또한. 이러한 파동의 분석은 소스, 수신기 또는 둘 모두가 매질에 대해 상대적으로 움직이는지 여부에 따라 달라진다. 수신기가 매질에 대해 정지하고 소스가 βs의 속도 매개변수로서 vs의 속도로 수신기에서 직접 멀어지는 시나리오가 주어지면 파장이 증가하고 관찰된 주파수 f는 다음에 의해 주어진다.
반면에, 소스가 고정되어 있고 수신기가 속도 매개변수 βr에 대해 vr의 속도로 소스에서 직접 멀어지는 시나리오가 주어지면 파장은 변경되지 않지만 에 대한 상대적인 파동의 전송 속도는 수신기가 감소하고 관찰된 주파수 f는 다음에 의해 주어진다.
빛은 소리나 물의 잔물결과 달리 매질을 통해 전파되지 않으며, 수신기에서 멀어지는 소스와 소스에서 멀어지는 수신기의 구분이 없다. 그림 3-6은 속도 매개변수 β를 사용하여 수신기에서 소스를 분리하는 상대론적 시공간 다이어그램을 보여준다. 따라서 시간 w에서 소스와 수신기 사이의 간격은 βw이다. 시간 팽창 때문에 . 녹색 광선의 기울기는 -1이므로 . 따라서 상대론적 도플러 효과(relativistic Doppler effect)는[41]:58–59
횡방향 도플러 효과[편집]
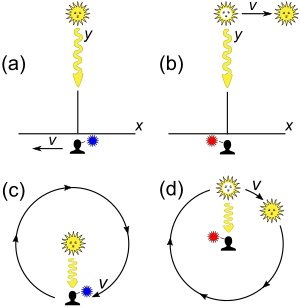
교차하지 않는 선을 따라 균일한 관성 운동으로 서로 접근하는 소스와 수신기가 서로 가장 가깝게 접근하고 있다고 가정한다. 고전적 분석은 수신기가 도플러 이동을 감지하지 못하는 것으로 예측된다. 분석의 미묘함 때문에 그 기대가 반드시 사실은 아니다. 그럼에도 불구하고, 적절하게 정의되면 횡방향 도플러 이동은 고전적 유사성이 없는 상대론적 효과이다. 미묘함은 다음과 같다.[45]:541–543
- 그림 3-7a. 수신기가 소스에 기하학적으로 가장 가까운 위치에 있을 때 주파수 측정값은 무엇인가? 이 시나리오는 소스의 프레임 S'에서 가장 쉽게 분석된다.[노트 10]
- 그림 3-7b. 수신기가 소스에 가장 가까운 것으로 보는 주파수 측정값은 무엇인가? 이 시나리오는 수신기의 프레임 S에서 가장 쉽게 분석된다.
횡방향 도플러 이동에 대한 논의에는 일반적으로 두 가지 다른 시나리오들이 검토된다:
- 그림 3-7c. 만일 수신기가 소스를 중심으로 원을 그리며 움직인다면, 수신기가 측정하는 주파수는 무엇인가?
- 그림 3-7d. 만일 소스가 수신기를 중심으로 원을 그리며 움직인다면, 수신기가 측정하는 주파수는 무엇인가?
시나리오 (a)에서 가장 가까운 접근 지점은 프레임에 독립적이며 시간에 대한 거리의 변화가 없는 순간을 나타내고(즉, dr/dt = 0 여기서 r은 수신기와 소스 사이의 거리) 따라서 종방향 도플러 효과는 없다. 소스는 수신기가 주파수 f′의 빛에 의해 조명되는 것으로 관찰하지만 수신기는 시간-팽창된 시계를 갖는 것으로 관찰한다. 따라서 프레임 S에서, 수신기는 주파수의 청색편이 광에 의해서 조명된다.
시나리오 (b)에서 그림은 광원이 이동했음에도 불구하고 광원이 수신기에 가장 가까웠을 때의 빛에 의해 수신기가 조명되는 것을 보여준다. 소스의 시계는 프레임 S에서 측정된 시간 확장되고 이 지점에서 dr/dt가 0과 같기 때문에 가장 가까운 지점에서 방출되는 소스의 빛은 주파수에 따라 적색편이된다.
시나리오 (c)와 (d)는 간단한 시간 팽창 논의들에 의해서 분석할 수 있다. (c)에서는, 수신기는 광원의 빛이 한 γ의 계수로 청색편이되고, 또한 (d)에서, 그 빛은 적색편이된다. 유일한 겉으로의 복잡성은 궤도를 도는 물체가 가속 운동을 한다는 것이다. 그렇지만, 만일 관성 관찰자가 가속하는 시계를 본다면, 시간 팽창을 계산할 때는 시계의 순간 속도만 중요하다. (그러나 그 반대는 사실이 아니다.)[45]:541–543 횡방향 도플러 이동에 대한 대부분의 보고서들은 그 효과를 한 적색편이로 언급하고 또한 시나리오 (b) 또는 (d)의 관점에서 그 효과를 분석한다.[노트 11]
에너지와 운동량[편집]
운동량을 사차원으로 확장하기[편집]

고전 역학에서 입자의 운동 상태는 질량과 속도에 의해 특징지어진다. 입자의 질량과 속도의 곱인 선형 운동량은 속도와 같은 방향을 갖는 벡터 양이다: p = mv. 이는 '보존된' 양으로, 닫힌계는 외부 힘의 영향을 받지 않으면 전체 선형 운동량이 변경될 수 없음을 의미한다.
상대론적 역학에서는, 운동량 벡터는 4차원으로 확장된다. 운동량 벡터에 추가된 시간 구성요소는 시공간 운동량 벡터가 시공간 위치 벡터 처럼 변환되도록 한다. 시공간 운동량의 속성을 탐구할 때 우리는 그림 3-8a에서 입자가 정지 상태에서 어떻게 보이는지 조사하는 것으로 시작한다. 정지 프레임에서 운동량의 공간적 성분은 영, 즉 p = 0 이지만 시간 성분은 mc와 같다.
우리는 로런츠 변환을 사용함으로써 이동하는 프레임에서 이 벡터의 변환된 구성 요소를 얻거나 또는 우리가 및 임을 알기 때문에 그림에서 직접 읽을 수 있으니, 이는 빨간색 축들이 감마에 의해 재조정되기 때문이다. 그림 3-8b는 이동하는 프레임에 나타나는 상황을 보여준다. 이동하는 프레임의 속도가 c 에 가까워짐에 따라 4-운동량의 공간 및 시간 구성 요소가 무한대로 이동하는 것이 명백하다.[41]:84–87
우리는 사차원 운동량에 대한 표현을 얻기 위해 이 정보를 곧 사용할 것이다.
빛의 운동량[편집]
빛 입자 또는 광자는 일반적으로 광속으로 알려진 상수인 c의 속도로 이동한다. 이 진술은 헌 동어반복이 아니다. 왜냐하면 많은 현대의 상대성 이론 공식은 일정한 광속을 가정으로 시작하지 않기 때문이다. 광자는 따라서 빛꼴 세계선을 따라 전파되며, 또한 적절한 단위들로, 모든 관찰자에게 동일한 공간 및 시간 구성 요소를 갖는다.
전자기학의 맥스웰 방정식의 결과는 빛이 에너지와 운동량을 전달하며, 또한 그 비율은 한 상수라는 것이다: . 를 재배열하면, 광자의 경우, 공간 및 시간 성분들이 동일하므로, E/c는 따라서 시공간 운동량 벡터의 시간 성분과 동일해야 한다.
광자는 빛의 속도로 이동하지만 유한한 운동량과 에너지를 가지고 있다. 그러기 위해서는, γmc의 질량 항은 영이어야 하며, 이는 광자들이 무질량 입자(massless particle)들임을 의미한다. 무한대 곱하기 영은 잘 정의되지 않은 양이지만, 그러나 E/c는 잘 정의되어 있다.
이 분석에 따르면, 만일 정지 프레임에서 광자의 에너지가 E와 같으면, 그것은 한 이동하는 프레임에서 와 같다. 이 결과는 그림 3-9를 확인하거나 로런츠 변환을 적용하여 도출할 수 있으며, 이전에 제공된 도플러 효과 분석과 일치한다.[41]:88
질량-에너지 관계[편집]
상대론적 운동량 벡터의 다양한 구성 요소들 간의 상호 관계들의 고려는 아인슈타인이 몇 가지 유명한 결론들을 내리도록 이끌었다.
- 저속 제한에서 β = v/c가 영에 접근하면, γ가 1에 접근하므로, 상대론적 운동량의 공간적 성분 는 운동량에 대한 고전적인 용어인 mv에 접근한다. 이러한 관점에서 볼 때 γm은 m의 상대주의적 일반화로 해석될 수 있다. 아인슈타인은 공식 에 따라 물체의 상대론적 질량(relativistic mass)이 속도에 따라 증가한다고 제안했다.
- 마찬가지로 상대론적 운동량의 시간 성분과 광자의 시간 성분을 비교하면, , 그래서 아인슈타인은 . 속도가 영인 경우로 단순화하면, 이것은 에너지와 질량에 관한 아인슈타인의 유명한 방정식이다.
질량과 에너지 사이의 관계를 보는 또 다른 방법은 저속에서 γmc2 의 급수 전개를 고려하는 것이다:
두 번째 항은 입자의 운동 에너지에 대한 표현일 뿐이다. 질량은 실제로 에너지의 또 다른 형태인 것으로 보인다.[41]:90–92[43]:129–130,180
아인슈타인이 1905년에 도입한 상대론적 질량의 개념인 mrel은 전 세계의 입자 가속기에서(또는 실제로 고속 입자에 의존하는 모든 기기에서 충분히 검증되었지만, 전자현미경,[46] 구식 컬러 텔레비전 세트 등), 그럼에도 불구하고 다른 이론적 발전을 위한 기초 역할을 한 개념이 아니라는 점에서 물리학에서 유익한 개념으로 입증되지 않았다. 예를 들어, 상대론적 질량은 일반 상대성이론에서 아무런 역할도 하지 않는다.
이러한 이유로 대부분의 물리학자들은 교육학적 문제와 마찬가지로 현재 질량과 에너지의 관계를 언급할 때 다른 용어를 선호한다.[47] "상대론적 질량"은 더 이상 사용되지 않는 용어이다. "질량"이라는 용어는 그 자체로 정지 질량 또는 불변 질량을 나타내며, 또한 상대론적 운동량 벡터의 불변 길이와 같다. 공식으로 표현하면,
이 공식은 질량이 없는 입자와 질량이 있는 모든 입자에 적용된다. mrest가 영인 광자의 경우에는, 를 산출한다.[41]:90–92
사-운동량[편집]
질량과 에너지 사이의 밀접한 관계 때문에 사-운동량(4-운동량이라고도 불림)은 에너지-운동량 4-벡터라고도 블린다. 4-운동량을 나타내기 위해 대문자 P를 사용하고 공간 운동량을 나타내기 위해 소문자 p를 사용하여 사-운동량은 다음과 같이 쓸 수 있다.
- 또는 대안으로,
- [43]:129–130,180
보존 법칙들[편집]
물리학에서, 보존 법칙들은 격리된 물리적 시스템의 어떤 특정한 측정 가능한 속성은 시스템이 시간이 지남에 따라 진화해도 변하지 않는다는 것을 진술한다. 1915년에, 에미 뇌터는 각 보존 법칙의 기초가 되는 자연의 한 근본적인 대칭성을 발견했다.[48] 물리적 과정이 공간 내의 어디서 발생하는지 상관하지 않는다는 사실(공간 평행이동 대칭(space translation symmetry))은 운동량 보존을 산출하고, 그러한 과정이 언제 발생하는지 상관하지 않는다는 사실(시간 평행이동 대칭(time translation symmetry))은 에너지의 보존을 산출한다 등. 이 섹션에서는, 우리는 상대론적 관점에서 질량, 운동량 및 에너지의 보존에 대한 뉴턴의 관점을 검토한다.
총 운동량[편집]
운동량 보존에 대한 뉴턴의 관점이 상대론적 맥락에서 어떻게 수정되어야 하는지 이해하기 위해 우리는 한 단일 차원으로 제한된 두 개의 충돌하는 물체들의 문제를 검토한다.
뉴턴 역학에서는, 최소 복잡성의 수학을 산출하는 이 문제의 두 가지 극단적인 경우들이 구별될 수 있다:
- (1) 두 물체들은 완전히 탄성 충돌로 서로 반동한다.
- (2) 두 물체들이 서로 달라붙고 또한 하나의 입자처럼 계속 움직인다. 이 두 번째 경우는 완전 비탄성 충돌의 경우이다.
(1)과 (2)의 경우 모두 운동량, 질량 및 총 에너지가 보존된다. 그렇지만, 비탄성 충돌의 경우 운동 에너지는 보존되지 않는다. 초기 운동 에너지의 어떤 부분은 열로 변환된다.
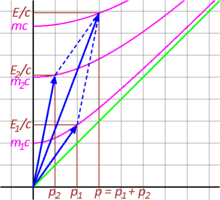
(2)의 경우, 운동량이 및 인 두 질량들이 충돌하여 보존된 질량 이 원래 시스템의 질량 중심의 속도로 이동하는 한 단일 입자를 형성한다. 총 운동량 는 보존된다.
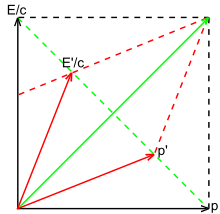
그림 3-10은 상대론적 관점에서 두 입자의 비탄성 충돌을 도해한다. 시간 성분들 및 는 결과 벡터의 총 E/c에 합산되며, 이는 에너지가 보존됨을 의미한다. 마찬가지로, 공간 구성요소 및 는 합산하여 결과의 벡터 p를 형성한다. 4-운동량은, 예상대로, 한 보존된 양이다. 그렇지만, 총 운동량의 불변 쌍곡선이 에너지 축과 교차하는 점에 의해 주어진 융합 입자의 불변 질량은 충돌한 개별 입자의 불변 질량의 합과 같지 않다. 과연, 그것은 개별 질량의 합보다 크다: .[41]:94–97
이 시나리오의 사건을 역순으로 살펴보면, 우리는 질량의 비-보존이 일반적으로 발생한다는 것을 알 수 있다: 불안정한 기본 입자가 자발적으로 두 개의 더 가벼운 입자로 붕괴할 때, 총 에너지는 보존되지만, 그러나 질량은 보존되지 않는다. 질량의 일부는 운동 에너지로 변환된다.[43]:134–138
기준 프레임들의 선택[편집]
분석을 수행할 프레임을 자유롭게 선택할 수 있으므로 특히 편리한 프레임을 선택할 수 있다. 운동량 및 에너지 문제를 분석할 때 가장 편리한 프레임은 일반적으로 "운동량 중심 프레임(center-of-momentum frame)"(영 운동량프레임 또는 COM(center of momentum) 프레임라고도 함)이다. 이것은 시스템의 전체 운동량의 공간 성분이 영인 프레임이다. 그림 3-11은 고속 입자가 두 개의 딸 입자들로 분해되는 것을 도해한다. 실험실 프레임에서 딸 입자들은 원래 입자의 궤적을 따라 지향된 방향으로 우선적으로 방출된다. 그렇지만, COM 프레임에서는, 질량들과 속도들의 크기가 일반적으로 동일하지 않지만, 두 개의 딸 입자들은 반대 방향으로 방출된다.
에너지 및 운동량 보존[편집]
상호 작용하는 입자들에 대한 뉴턴식 분석에서는, 프레임들 간의 변환은 모든 속도들에 갈릴레이 변환을 적용하기만 하면 되므로 간단하다. 이므로, 운동량 . 만일 상호 작용하는 입자들 시스템의 총 운동량이 한 프레임에서 보존되는 것으로 관찰되면, 다른 프레임에서도 마찬가지로 보존되는 것으로 관찰된다.[43]:241–245
COM 프레임에서 운동량의 보존은 충돌 전후 둘 다 p = 0이라는 요건에 해당한다. 뉴턴 분석에서는, 질량 보존은 를 지시한다. 우리가 고려하고 있는 단순화된 일차원 시나리오에서는, 입자의 나가는 운동량들을 결정하기 전에 하나의 추가 제약 조건-한 에너지 조건만 필요하다. 운동 에너지의 손실이 없는 완전 탄성 충돌의 일차원 경우에는, COM계에서 반발 입자의 나가는 속도들은 들어오는 속도들과 정확히 동일하고 반대이다. 운동 에너지가 완전히 손실된 완전 비탄성 충돌의 경우에는, 반동 입자들의 나가는 속도는 영이 된다.[43]:241–245
로 계산되는 뉴턴 운동량은 로런츠 변환에서 제대로 작동하지 않는다. 속도들의 선형 변환 는 고도의 비선형 으로 대체되고 그래서 한 프레임에서 운동량 보존을 증명하는 어떤 계산은 다른 프레임들에서는 유효하지 않다. 아인슈타인은 운동량 보존을 포기하거나 또는 운동량의 정의를 변경해야 하는 상황에 직면했다. 이 두 번째 옵션이 그가 선택한 것이다.[41]:104
에너지 및 운동량에 대한 상대론적 보존 법칙은 에너지, 운동량 및 질량에 대한 세 가지 고전적인 보존 법칙을 대체한다. 질량은 전체 상대론적 에너지에 포함되었기 때문에 더 이상 독립적으로 보존되지 않는다. 이것은 에너지의 상대론적 보존을 비상대론적 역학보다 더 간단한 개념으로 만드는데, 왜냐하면 총 에너지는 아무런 조건들 없이 보존되기 때문이다. 열 또는 내부 위치 에너지로 변환된 운동 에너지는 질량 증가로 나타난다.[43]:127
예: 질량과 에너지의 동등성 때문에 기본 입자 질량은 일반적으로 에너지 단위로 표시되며, 여기서 1 MeV = 106 전자 볼트이다. 한 하전 파이온은 질량이 139.57MeV(전자 질량의 약 273배)인 입자이다. 그것은 불안정하고, 또한 질량이 105.66MeV(전자 질량의 약 207배)인 뮤온과 거의 무시할 수 있는 질량을 갖는 한 반중성미자로 붕괴한다. 파이온 질량과 뮤온 질량의 차이는 33.91MeV이다.
그림 3-12a는 파이온의 정지 프레임에서 이러한 붕괴 반응에 대한 에너지-운동량 도표를 보여준다. 무시할 수 있는 질량 때문에 중성미자는 빛의 속도에 매우 가깝게 이동한다. 광자의 에너지와 같은 에너지에 대한 상대론적 표현은 이고, 이것은 또한 운동량의 공간 성분 값이기도 하다. 운동량을 보존하기 위해서, 뮤온은 중성미자 운동량의 공간 성분과 같은 값을 갖지만, 반대 방향으로이다.
이 붕괴 반응의 에너지에 대한 대수적 분석들은 온라인에서 볼 수 있고,[49] 그래서 그림 3-12b은 대신 그래프 계산기 해를 제공한다. 중성미자의 에너지는 29.79 MeV이고, 또한 뮤온의 에너지는 33.91 MeV − 29.79 MeV = 4.12 MeV이다. 대부분의 에너지는 영-근사-질량인 중성미자에 의해서 운반된다.
기본을 넘어서[편집]
이 섹션의 주제들은 이전 섹션의 주제들보다 기술적 난이도가 훨씬 높으며 휘어진 시공간의 입문의 이해에 필수적이지는 않다.
신속도[편집]
로런츠 변환은 한 기준 프레임의 사건 좌표를 다른 프레임의 좌표와 연결한다. 속도의 상대론적 구성은 두 속도를 더하는 데 사용된다. 후자의 계산을 수행하는 공식은 비선형이므로 해당 갈릴레이 공식보다 더 복잡하다.
이 비선형성은 우리가 선택한 매개변수의 인공물이다.[9]:47–59 우리는 이전에 x–ct 시공간 다이어그램에서, 원점에서 일정한 시공간 간격에 있는 점들이 불변 쌍곡선을 형성한는 것에 주목했다. 우리는 또한 표준 구성에서 두 시공간 기준 프레임들의 좌표계가 서로에 대해 쌍곡선으로 회전한다는 것도 주목했다.
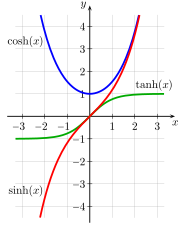
이러한 관계를 표현하기 위한 자연 함수는 삼각함수의 쌍곡선 유사 함수(hyperbolic analogs)이다. 그림 4-1a는 sin(a) 및 cos(a)가 있는 단위원을 보여준다. 이 다이어그램과 기본 삼각법의 익숙한 단위 원 사이의 유일한 차이점은 다음과 같다. a는 광선과 x-axis 사이의 각도가 아니라 x-축. (숫자적으로, 단위 원에 대한 각도와 2 × 면적 측정은 동일하다.) 그림 4-1b는 sinh(a) 및 cosh(a)가 있는 단위 쌍곡선(unit hyperbola)을 보여준다. 여기서 a는 마찬가지로 두 배의 착색된 영역으로 해석된다.[50] 그림 4-2는 sinh, cosh, tanh 함수의 플롯을 보여준다.
단위원의 경우, 광선의 기울기는 다음으로 주어진다
데카르트 평면에서, 점 (x, y)의 각도 θ만큼 회전은 점 (x′, y′)에서 다음으로 주어진다
시공간 다이어그램에서 속도 매개변수 는 기울기의 유사체이다. 신속도 φ는 다음으로 주어진다[43]:96–99
여기서
위에서 정의한 신속도는 특수 상대성이론에서 많은 표현이 그 관점에서 표현될 때 상당히 더 단순한 형태를 취하기 때문에 매우 유용하다. 예를 들어, 신속도는 공선 속도-가산식에서 단순히 가산된다;[9]:47–59
혹은 다르게 말하면,
로런츠 변환은 신속도의 관점에서 표현될 때 한 간단한 형태를 취한다. γ 계수는 다음과 같이 쓸 수 있다.
공간 좌표축의 회전 없이 균일한 속도로 상대 운동을 설명하는 변환을 부스트라고 불린다.
γ 및 γβ를 이전에 제시된 변환에 대입하고 행렬 형식으로 다시 작성하면 x 방향의 로런츠 부스트는 다음과 같이 쓸 수 있다
그리고 x방향의 역로렌츠 부스트는 다음과 같이 쓸 수 있다
즉, 로렌츠 부스트는 민코프스키 시공간에서 쌍곡선 회전(hyperbolic rotation)을 나타낸다.[43]:96–99
쌍곡선 함수들을 사용하는 이점은 테일러Taylor와 휠러Wheeler의 고전적인 교과서들와 같은 일부 책들에서 매우 초기 단계에서 그것들의 사용을 소개한다는 것이다.[9][51][노트 12]
4-벡터[편집]
사차원 벡터는 위에서 에너지-운동량 4-벡터의 맥락에서 언급되었지만, 크게 강조하지는 않았다. 사실, 특수 상대성이론의 기본 유도들의 어느 것도 그것들을 필요로 하지 않는다. 그러나 일단 이해되면, 4-벡터, 더 일반적으로 텐서는 특수 상대성이론에 대한 수학과 개념적 이해를 크게 단순화한다. 이러한 객체로 독점적으로 작업하면 명백하게 상대론적으로 불변인 공식들을 도출하며, 이는 자명하지 않지 문맥들에서는 상당한 이점이 된다. 예를 들어, 일반적인 형태의 맥스웰 방정식의 상대론적 불변성을 입증하는 것은 자명한 일은 아니고, 전자기장 텐서 공식을 사용한 일상적인 계산(실제로는 관찰에 불과함)일 뿐이다. 반면 일반 상대성이론은 처음부터 물리적으로 관련된 개체를 나타내는 4-벡터, 보다 일반적으로는 텐서에 크게 의존한다. 특정 좌표에 의존하지 않는 방정식을 통해 이들을 연관시키려면 특수 상대성이론에서와 같이 평평한 시공간이 아니라 휘어진 시공간 내에서도 이러한 4-벡터를 연결할 수 있는 텐서가 필요하다. 텐서에 대한 연구는 시공간에 대한 기본적 논의만 제공하는 이 글의 범위를 벗어난다.
4-벡터들의 정의[편집]
구성 요소 "Ai"가 로런츠 변환에 따라 계 간에 변환되면 4-튜플 은 "4-벡터"이다.
만일 좌표를 사용하면서, 다음에 따라 x-방향으로 변환하면 A는 4–벡터이다
이는 로런츠 변환의 이전 설명에서 ct를 A0로, x를 A1로 단순히 대체한 결과이다.
평소와 같이, 우리가 x, t 등을 쓸 때는 일반적으로 Δx, Δt 등을 의미한다.
한 4–벡터의 마지막 세 구성요소는 3차원 공간에서 표준 벡터이여야 한다. 따라서, 한 4–벡터는 회전들뿐만 아니라 로런츠 변환들에서도 와 같이 변환되어야만 한다.[37]:36–59
4-벡터의 속성들[편집]
- 선형 결합에서 닫힘: A와 B가 4-벡터이면 는 또한 4-벡터이다.
- 내적 불변: A와 B가 4-벡터이면 내적(스칼라 곱)은 불변이다. 즉, 내적은 계산되는 계과 무관하다. 내적 계산이 3-벡터의 내적 계산과 어떻게 다른지 확인하라. 다음에서 및 는 3-벡터이다.
- 로런츠 변환에서 불변인 것 외에도 위의 내적은 3-space에서의 회전에서도 또한 불변이다.
- 만일 이면 두 벡터를 직교라고 말한다. 3-벡터들의 경우와 달리, 4-벡터들은 서로 직각일 필요는 없다. 그 규칙은 만일 두 개의 4-벡터들이 한 광선의 세계선인 45°선에서 동일하고 반대 각도들만큼 오프셋되면 직교한다는 것이다. 이것은 한 빛꼴 4-벡터가 자체로 직교한다는 것을 의미한다.
- 한 벡터 크기의 불변성: 한 벡터의 크기는 4-벡터와 그 자체의 내적이며, 또한 어떤 프레임-독립적 속성이다. 간격들과 마찬가지로, 크기는 양수, 음수 또는 영일 수 있으므로, 벡터는 시간꼴, 공간꼴 또는 널(빛꼴)이라고 참조된다. 널 벡터는 영 벡터와 동일하지 않다. 널 벡터는 인 반면 영 벡터는 구성 요소가 모두 영인 벡터이다. 노름의 불변성을 보여주는 특별한 경우들은 불변 간격 와 또한 상대론적 운동량 벡터 의 불변 길이를 포함한다.[43]:178–181[37]:36–59
4-벡터의 예들[편집]
- 변위 4-벡터: 시공간 분리라고도 알려진 이것은 (Δt, Δx, Δy, Δz), 또는 무한소 분리들의 경우 (dt, dx, dy, dz).
- 속도 4-벡터: 변위 4-벡터를 로 나눈 결과이다. 여기서 는 dt, dx, dy 및 dz를 생성하는 두 사건들 사이의 고유 시간이다.
- 4-속도는 입자의 세계선에 접하고, 또한 입자의 프레임에서 시간의 일 단위와 같은 어떤 길이를 갖는다.
- 한 가속된 입자에는 항상 정지해 있는 관성 프레임이 없다. 그러나 순간적으로 입자와 함께 공변하는 관성 프레임은 항상 찾을 수 있다. 순간적 공변 기준 프레임(MCRF)이라는 이 프레임은 가속된 입자들의 분석에 특수 상대성이론을 적용할 수 있게 해준다.
- 광자는 널 선들에서 움직이기 때문에, 광자에 대한 및 4-벡터는 정의할 수 없다. 광자가 정지한 프레임은 없으며, 또한 한 광자의 경로를 따라 어떤 MCRF도 설정될 수 없다.
- 에너지-운동량 4-벡터:
- 앞에서 지적한 바와 같이, 에너지 운동량 4-벡터에 대한 다양한 처리가 있으므로 로 표현되기도 한다. 또는 첫 번째 성분은 주어진 프레임에서 입자(또는 입자 시스템)의 총 에너지(질량 포함)이고 나머지 구성 요소는 공간적 운동량. 에너지-운동량 4-벡터는 한 보존된 양이다.
- 가속 4-벡터: 에 대한 속도 4-벡터의 미분을 취한 결과이다.
- 힘 4-벡터: 에 대한 운동량 4-벡터의 미분이다.
4-벡터와 물리 법칙[편집]
특수 상대성이론의 첫 번째 가정은 모든 관성 프레임의 등가성을 선언한다. 한 계에 있는 물리적 법칙은 모든 프레임에 적용되어야 한다. 그렇지 않으면 프레임을 구별할 수 있기 때문이다. 뉴턴 운동량은 로런츠 변환에서 제대로 작동하지 않으며 아인슈타인은 운동량 보존을 포기하기보다 운동량 정의를 4-벡터를 포함하는 것으로 변경하는 것을 선호했다.
물리적 법칙은 프레임에 독립적인 구성을 기반으로 해야 한다. 이것은 물리 법칙이 항상 프레임 독립적인 스칼라를 연결하는 방정식의 형태를 취할 수 있음을 의미한다. 그렇지만, 4-벡터와 관련된 방정식들은 적절한 차수를 가진 텐서들을 사용해야 하며, 그 자체는 4-벡터들로부터 구성되는 것으로 생각될 수 있다.[43]:186
가속[편집]
특수 상대성이론은 관성 프레임에만 적용 가능하고 가속하는 물체나 가속하는 기준 프레임을 다룰 수 없다는 것은 일반적인 오해이다. 실제로 가속하는 물체는 일반적으로 가속 프레임을 전혀 다룰 필요 없이 분석할 수 있다. 일반 상대성이론이 필요한 것은 중력이 중요한 경우에만 가능하다.[52]
그러나 가속 프레임을 올바르게 처리하려면 약간의 주의가 필요하다. 특수 상대성이론과 일반 상대성이론의 차이점은 (1) 특수 상대성이론에서 모든 속도는 상대적이지만 가속도는 절대적이라는 것이다. (2) 일반 상대성이론에서 모든 운동은 관성, 가속 또는 회전 여부에 관계없이 상대적이다. 이 차이를 수용하기 위해 일반 상대성이론은 휘어진 시공간을 사용한다.[52]
이 섹션에서는 가속 기준 프레임 관련된 여러 시나리오를 분석한다.
드완-베란-벨 우주선 역설[편집]
드완-베란-벨 우주선 역설(벨의 우주선 역설)은 시공간적 접근의 기하학적 통찰력의 도움을 받지 않는 직관적 추론이 이슈화 될 수 있는 문제의 좋은 예이다.

그림 4-4에서 두 개의 동일한 우주선이 공간에 떠 있고 서로에 대해 정지해 있다. 그들은 끊어지기 전에 제한된 양의 스트레칭만 가능한 줄로 연결되어 있다. 우리의 프레임 즉 관찰자 프레임이 주어진 순간에 두 우주선은 동일한 일정한 고유 가속도를 갖는 선을 따라 같은 방향으로 가속한다.[노트 13] 그 줄은 끊어질 것인가?
역설이 새롭고 상대적으로 알려지지 않았을 때, 전문 물리학자들도 해법을 찾는 데 어려움을 겪었다. 두 노선의 추론은 반대 결론으로 이어진다. 아래에 나와 있는 주장 중 하나가 정답이지만 두 가지 모두 결함이 있다.[43]:106,120–122
- 정지한 프레임의 관찰자에게 우주선은 L 거리에서 시작하여 가속 중에 같은 거리를 유지한다. 가속 중 L은 가속하는 우주선의 프레임에서 거리 L' = γL만큼 길이가 축소된 거리이다. 충분히 오랜 시간이 지나면 γ는 줄이 끊어져야 할 만큼 충분히 큰 인자로 증가한다.
- A와 B를 앞뒤 우주선이라고 하자. 우주선의 계에서 각 우주선은 다른 우주선이 하고 있는 것과 동일한 작업을 수행하는 것을 본다. A는 B가 자신과 같은 가속도를 가지고 있다고 말하고, B는 A가 그녀의 모든 움직임과 일치한다고 본다. 따라서 우주선은 같은 거리를 유지하고 줄은 끊어지지 않는다.[43]:106,120–122
첫 번째 주장의 문제는 "우주선의 프레임"이 없다는 것이다. 두 우주선이 둘 사이의 거리를 측정하기 때문에 있을 수 없다. 우주선의 공통 프레임이 없기 때문에 줄의 길이가 잘못 정의된다. 그럼에도 불구하고 결론은 옳고 그 주장은 대부분 옳다. 그러나 두 번째 주장은 동시성의 상대성을 완전히 무시한다.[43]:106,120–122
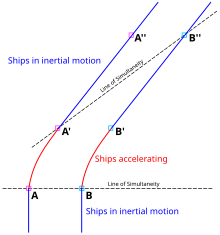
시공간 도표(그림 4-5)는 이 역설에 대한 올바른 해결책을 거의 즉시 명백하게 보여준다. 민코프스키 시공간의 두 관찰자는 고유 시간 동안 일정한 크기의 가속도로 가속한다(관성 관찰자가 아닌 관찰자가 직접 측정한 가속도 및 경과 시간). 그들은 이 단계 전후에 움직이고 관성적이다. 민코프스키 기하학에서 동시성 선을 따른 길이 는 동시성 선을 따른 길이 보다 크다.
길이 증가는 로런츠 변환의 도움으로 계산할 수 있다. 그림 4-5와 같이 가속이 완료되면 우주선은 계에서 일정한 오프셋을 유지한다.</math> 및 는 의 우주선 위치이고, 계의 위치는 다음과 같다.[53]
말하자면 "역설"은 벨이 자신의 예를 구성한 방식에서 비롯된다. 로런츠 수축에 대한 일반적인 논의에서 정지한 길이는 고정되고 이동하는 길이는 프레임 에서 측정한 대로 짧아진다. 그림 4-5에서 볼 수 있듯이 벨의 예는 프레임 에서 측정된 이동하는 길이 와 는 고정되며 따라서 프레임 의 정지한 프레임 길이 를 강제로 증가시킨다고 주장한다.
지평선이 있는 가속된 관찰자[편집]
특정 특수 상대성이론 문제 설정은 사건 지평선과 같이 일반적으로 일반 상대성이론과 관련된 현상에 대한 통찰력으로 이어질 수 있다. 그림 2-7에 첨부된 텍스트에서 자홍색 쌍곡선은 시공간에 끊임없이 가속하는 여행자가 추적하는 실제 경로를 나타낸다. 양의 가속도 기간 동안 여행자의 속도는 단지 빛의 속도에 '접근'하는 반면, 우리 프레임에서 측정하면 여행자의 가속도는 지속적으로 감소한다.
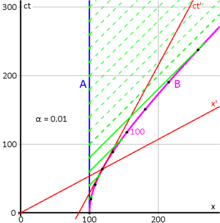
그림 4-6은 여행자 동작의 다양한 기능을 보다 구체적으로 자세히 설명한다. 임의의 주어진 순간에 그녀의 공간 축은 쌍곡선 상의 원점과 그녀의 현재 위치를 지나는 선에 의해 형성되고, 그녀의 시간 축은 그녀의 위치에서 쌍곡선에 대한 접선이다. 속도 매개변수 는 가 증가함에 따라 1의 한계에 접근한다. 마찬가지로 는 무한대에 접근한다.
불변 쌍곡선의 모양은 일정한 고유 가속도의 경로에 해당한다. 이것은 다음과 같이 증명할 수 있다:
- 우리는 를 기악한다.
- 이므로 우리는 라고 결론짓는다.
- 상대론적 힘의 법칙으로부터,
- 단계 2로부터 를 치환하면 단계 3으로부터 의 표현은 상수 표현인 를 산출한다.[41]:110–113
그림 4-6은 계산된 특정 시나리오를 보여준다. 테렌스(A)와 스텔라(B)는 처음에 원점에서 100광시간 떨어져 함께 서 있다. 스텔라는 시간 0에 이륙하고 우주선은 시간당 0.01c로 가속된다. 20시간마다 테렌스 라디오는 집의 상황에 대해 스텔라에게 업데이트한다(녹색 실선). 스텔라는 이러한 정기적인 전송을 수신하지만 거리가 증가하면(시간 팽창에 의해 부분적으로 상쇄됨) 그녀는 그녀의 시계로 측정한 대로 나중에 테렌스의 통신을 받게 되며 그의 시계(녹색 점선)로 100시간 후에는 테렌스로부터 어떠한 통신도 결코 받지 못한다.[41]:110–113
테렌스의 시계로 100시간 후, 스텔라는 어두운 영역에 들어간다. 그녀는 테렌스의 시간꼴 미래의 밖에서 여행했다. 반면에 테렌스는 스텔라가 그에게 보내는 메시지를 계속해서 받기가 가능하다. 단지 그는 충분히 오래 기다려야만 한다. 시공간은 겉보기 사건의 지평선에 의해 분리된 별개의 영역으로 분할되었다. 스텔라가 가속을 계속하는 한 그녀는 이 지평선 뒤에서 무슨 일이 일어나는지 결코 알 수 없다.[41]:110–113
휘어진 시공간으로 입문[편집]
기본 명제[편집]
뉴턴의 이론은 모든 공간과 시간에 걸쳐 확장되는 강성의 유클리드 기준 프레임을 배경으로 운동이 발생한다고 가정했다. 중력은 거리를 가로질러 순간적으로 작용하는 신비한 힘에 의해 매개되며, 그 작용은 중간 공간과 무관하다.[노트 14] 대조적으로, 아인슈타인은 공간 전체에 걸쳐 확장되는 배경 유클리드 기준 프레임이 있다는 것을 부인했다. 중력과 같은 것은 없으며 시공간 자체의 구조만 있을 뿐이다.[9]:175–190
시공간 관점에서, 지구 궤도를 도는 위성의 경로는 지구, 달, 태양의 먼 영향에 의해 결정되지 않는다. 대신, 위성은 오직 지역 조건에 반응하여 우주를 이동한다. 시공간은 충분히 작은 규모로 볼 때 국소적으로 평평하기 때문에, 위성은 항상 국소 관성 프레임에서는 직선을 따른다. 우리는 위성이 항상 측지선의 경로를 따라간다고 말한다. 단일 입자의 운동을 따라가는 중력의 증거는 발견할 수 없다.[9]:175–190
시공간에 대한 모든 분석에서, 중력의 증거는 두 물체 또는 두 개의 분리된 입자의 상대 가속도를 관찰할 것을 요구한다. 그림 5-1에서, 지구의 중력장에서 자유낙하하는 두 개의 분리된 입자는 중력장의 국소적 이질성으로 인해 조석 가속도를 나타내어 각 입자가 시공간의 다른 경로를 따르도록 한다. 이 입자들이 서로에 대해 나타내는 조석 가속도는 설명을 위해 힘을 필요로 하지 않는다. 오히려, 아인슈타인은 그것들을 시공간의 기하학, 즉 시공간의 곡률로 기술했다. 이러한 조석 가속들은 엄격하게 국소적이다. 지구로부터 먼 거리 영역에 작용하는 중력의 나타남을 결과하는 것은 곡률의 많은 국소적 표명들의 누적된 총 효과이다.[9]:175–190
일반 상대성이론의 바탕에는 두 가지 중심 명제가 있다.
- 첫 번째 중요한 개념은 좌표 독립성이다. 물리 법칙은 사용하는 좌표계에 의존할 수 없다. 이것은 비가속(관성) 기준 프레임에서 움직이는 모든 관찰자에 대해 물리 법칙이 동일해야 한다는 특수 상대성 이론에서 사용된 버전의 상대성 원리의 주요 확장이다. 일반 상대성이론에서 아인슈타인 자신의 (번역된) 단어를 사용하려면 "물리 법칙은 어떤 종류의 운동에서도 기준 프레임에 적용할 수 있는 성질을 가져야 한다."[54]:113 이것은 즉각적인 문제로 이어진다. 가속 프레임에서 우리는 절대적인 의미에서 가속 상태를 평가할 수 있게 해주는 것처럼 보이는 힘을 느낀다. 아인슈타인은 등가의 원리를 통해 이 문제를 해결했다.[55]:137–149

- 등가원리는 공간의 충분히 작은 영역에서 중력의 영향은 가속도의 영향과 동일하다는 것이다.
- 그림 5-2에서 사람 A는 g의 균일한 가속도를 받는 우주선에 있고 무거운 물체로부터 멀리 떨어져 있다. 사람 B는 지구상에 정지한 상자 안에 있다. 우주선이 충분히 작아서 조석 효과가 측정불가라면(현재 중력 측정 장비의 감도를 고려할 때 A와 B는 아마도 릴리푸티안(Lilliputian)-걸리버 여행기 소인국인-이어야 함), A와 B는 그들이 어떤 설정에 있는지 알기 위해 수행할 수 있는 실험은 없다[55]:141–149
- 등가 원리의 다른 표현은 뉴턴의 만유인력 법칙 F = GMmg/r2 = mgg 및 뉴턴의 제2법칙 F = mia에서는 중력 질량 mg이 관성 질량 mi과 같아야 하는 선험적a priori 이유가 없음에 주목하는 것이다. 등가 원칙에 따르면 이 두 질량은 동일하다.[55]:141–149
위의 곡선 시공간에 대한 기초적 설명으로부터 중력에 대한 완전한 설명으로 가려면 텐서 미적분학 및 미분 기하학이 필요하며, 두 주제들 모두 상당한 연구를 필요로 한다. 이러한 수학적 도구들이 없으면 일반 상대성이론에 대해서 쓸 수는 있지만 자명하지 않은 유도들을 논증하는 것은 불가능하다.
시간의 곡률[편집]
특수 상대성이론에 대한 논의에서 힘은 배경 역할에 불과했다. 특수 상대성이론은 모든 시공간을 채우는 관성 프레임을 정의할 수 있는 능력을 가정한다. 이게 정말 가능할까? 불균일한 중력장에서 실험에 따르면 답은 아니오이다. 중력장은 대역적global 관성 프레임을 구성하는 것을 불가능하게 만든다. 시공간의 충분히 작은 영역에서 국소적 관성 프레임은 여전히 가능하다. 일반 상대성이론은 이러한 국소 프레임을 체계적으로 연결하여 시공간의 보다 일반적인 그림으로 만드는 것을 포함한다.[37]:118–126
1916년 일반 상대성이론이 발표되기 몇 년 전, 아인슈타인은 등가원리를 사용하여 다음 사고 실험에서 중력 적색편이의 존재를 예측했다: (i) 높이 h(그림 5-3)의 타워가 건설되었다고 가정한다. (ii) 탑 꼭대기에서 정지 질량 m의 입자를 떨어뜨린다. 가속도 g로 자유 낙하하며, v = (2gh)1/2 속도로 지면에 도달하므로 지상에서 관찰자가 측정한 총 에너지 E는 (iii) 질량-에너지 변환기는 입자의 총 에너지를 위쪽으로 향하는 단일 고에너지 광자로 변환한다. (iv) 타워 꼭대기에서 에너지-질량 변환기는 광자 E'의 에너지를 다시 정지 질량 m'의 입자로 변환한다.[37]:118–126
m = m'이어야 한다. 그렇지 않으면 영구 기관 장치를 구성할 수 있기 때문이다. 따라서 우리는 E' = m라고 예측하므로
지구의 중력장에서 상승하는 광자는 에너지를 잃고 적색편이된다. 천문학적 관찰을 통해 이 적색편이를 측정하려는 초기 시도는 다소 결정적이지 않았지만 파운드-레브카Pound-Rebka (1959)와 나중에 파운드-스나이더Pound-Snider (1964)에 의해 결정적인 실험실 관찰이 수행되었다.[56]
빛에는 연관된 주파수가 있으며 이 주파수는 시계 작동을 구동하는 데 사용될 수 있다. 중력적 적색편이는 시간 자체에 대한 중요한 결론으로 이어진다. 중력은 시간을 느리게 만든다. 속도가 안정적인 원자 전이에 의해 제어되는 두 개의 동일한 시계를 구축한다고 가정한다. 하나의 시계는 타워 위에 놓고 다른 시계는 바닥에 둔다. 타워 꼭대기에 있는 실험자는 지상 시계의 신호가 타워에 있는 그녀 옆에 있는 시계의 신호보다 주파수가 더 낮은 것을 관찰했다. 탑을 올라가는 빛은 파동일 뿐이고, 올라가는 길에 파동의 마루가 사라지는 것은 불가능하다. 정확히 많은 빛의 진동이 바닥에서 방출된 만큼 타워의 꼭대기에 도달한다. 실험자는 지상 시계가 느리게 작동하고 있으며 지상 시계와 나란히 비교하기 위해 시계탑 시계를 내려서 이를 확인할 수 있다.[3]:16–18 1km 타워의 경우 불일치는 현대식 기기로 쉽게 측정 가능한 약 하루 9.4나노초에 이른다.
중력장의 시계는 모두 같은 속도로 작동하지 않는다. 파운드-레브카실험과 같은 실험은 시공간의 시간 성분의 곡률을 확고히 확립했다. 파운드-레브카 실험은 시공간의 공간 구성요소의 곡률에 대해 아무 말도 하지 않는다. 그러나 중력 시간 팽창을 예측하는 이론적 주장은 일반 상대성이론의 세부 사항에 전혀 의존하지 않는다. 중력 이론은 등가의 원리를 존중한다면 중력 시간 팽창을 예측할 것이다.[3]:16 여기에는 뉴턴 중력이 포함된다. 일반 상대성이론의 표준 시연은 "뉴턴 한계(Newtonian limit)"(즉, 입자는 천천히 움직이고 중력장은 약하고 장은 정적임)에서 시간의 곡률만으로도 뉴턴의 중력 법칙을 도출하기에 충분하다는 것을 보여주는 것이다.[57]:101–106
뉴턴 중력은 곡선 시간 이론이다. 일반 상대성이론은 휘어진 시간과 휘어진 공간의 이론이다. G를 중력 상수로, M을 뉴턴적 별의 질량으로, 별에서 r 거리에 있는 미미한 질량의 궤도를 도는 천체가 주어지면 뉴턴 중력의 시공간 간격은 시간 계수만 가변적이다:[3]:229–232
공간의 곡률[편집]
앞의 계수는 뉴턴 중력의 시간축 곡률을 설명하며, 이 곡률은 모든 뉴턴 중력 효과를 완전히 설명한다. 예상대로 이 보정 계수는 와 에 정비례하며 분모의 때문에 보정 계수는 1만큼 증가한다. 중력에 접근한다는 것은 시간이 곡선이라는 뜻이다.
그러나 일반 상대성이론은 휘어진 공간 및 휘어진 시간에 대한 이론이므로 위에서 제시한 시공간의 공간적 성분을 수식하는 용어가 있다면, 말하자면, 공간적 항에 적용되는 곡률 보정 인자로 인해 행성 및 위성 궤도에 그 영향을 보아야 하지 않을까?
대답은 '있다'는 것이지만 효과는 미미하다. 그 이유는 행성의 속도는 빛의 속도에 비해 매우 작아서 태양계의 행성과 위성의 경우 항이 공간적 항을 왜소하게 만들기 때문이다.[3]:234–238
공간적 항의 미세함에도 불구하고 뉴턴 중력에 문제가 있다는 첫 번째 징후는 150여 년 전에 발견되었다. 1859년 위르뱅 르베리에는 1697년부터 1848년까지 태양 원반 위의 수성의 통과에 대한 이용 가능한 시간 제한 관측 분석에서 알려진 물리학으로는 행성의 궤도를 설명할 수 없다고 보고했다. 수성의 궤도 내에 행성이나 소행성대가 존재하지 않는 한 수성 궤도의 근일점은 다른 행성의 잡아당김으로 설명될 수 있는 것보다 과도한 세차 운동을 나타냈다.[58] 이 변칙적인 세차 운동(태양세기당 단 43호초(arcsecond))의 미세한 값을 감지하고 정확하게 측정하는 능력은 19세기 위치천문학의 정교함을 보여준다.

천왕성 궤도의 흔들림을 분석하여 "펜 끝에서" 해왕성의 존재를 일찍 발견한 유명한 천문학자로서, 르베리에의 발표는 프로와 아마추어로서 20년에 걸친 "벌칸-매니아(Vulcan-mania)"의 시기를 촉발했다. 천문학자들은 모두 가상의 새로운 행성을 찾아 헤맸다. 이 검색에는 벌칸에 대한 여러 잘못된 목격이 포함되었다. 궁극적으로 그러한 행성이나 소행성대는 존재하지 않는다는 것이 확인되었다.[59]
1916년에, 아인슈타인은 수성의 이 변칙적인 세차 운동이 시공간의 곡률에 따른 공간적 항으로 설명된다는 것을 보여주어야 했다. 단순히 뉴턴 중력의 표현인 시간적 용어의 곡률은 이 변칙적인 세차 운동을 설명하는 데 아무런 역할도 하지 않는다. 그의 계산의 성공은 아인슈타인의 동료들에게 일반 상대성이론이 옳을 수 있다는 강력한 표시였다.
아인슈타인의 예측 중 가장 놀라운 것은 시공간 간격의 공간적 구성요소에 있는 곡률 항이 거대한 물체 주위의 빛의 굽힘으로 측정될 수 있다는 그의 계산이었다. 시공간 도표에서 빛의 기울기는 ±1이다. 공간에서의 움직임은 시간에서의 움직임과 같다. 불변 간격의 약한 장 표현을 위해서, 아인슈타인은 공간적 성분들에서 정확히 같으나 반대 부호 곡률을 계산했다.[3]:234–238
뉴턴의 중력에서, 앞의 계수는 별 주위의 빛의 휨을 예측한다. 일반 상대성이론에서 앞에 있는 계수는 총 굽힘의 배가(doubling)를 예측한다.[3]:234–238
1919년 에딩턴 일식 탐험과 아인슈타인의 명성 상승에 대한 이야기는 다른 곳에서 잘 알려져 있다.[60]
시공간 곡률의 소스들[편집]

대조적으로, 일반 상대성이론은 질량 외에 시공간 곡률의 여러 원인을 식별한다. 아인슈타인 장 방정식() 에서, 중력의 근원은 오른쪽에 표시되는 , 에너지-운동량 텐서이다.
그림 5-5는 에너지-운동량 텐서 성분들에서 중력의 다양한 근원을 분류한다.
- (빨간색): 입자 사이의 힘으로 인한 위치 에너지 및 임의의 열 운동으로 인한 운동 에너지에 대한 기여를 포함하는 총 질량-에너지 밀도.
- 및 (주황색): 운동량 밀도 항이다. 부피 유동(bulk movement)이 없더라도 열전도에 의해 에너지가 전달될 수 있으며 전도된 에너지는 운동량을 전달할 것이다.
- 는 j-방향으로의 단위 면적당 운동량의 i-성분의 흐름 속도이다. 부피 유동이 없더라도 입자의 무작위 열 운동은 운동량 흐름을 발생시키므로 i = j 항(녹색)은 등방성 압력을 나타내며, i ≠ j 항(파란색)은 전단 응력을 나타낸다.[61]
방정식에서 파생되어야 하는 한 가지 중요한 결론은 구어체로 말하면 중력 자체가 중력을 생성한다라는 것이다.[노트 15][57]:112–113 에너지는 질량을 갖는다. 뉴턴 중력에서도 중력장은 중력 위치 에너지라고 하는 에너지 와 관련이 있다. 일반 상대성이론에서 중력장의 에너지는 중력장의 생성으로 피드백된다. 이것은 방정식을 비선형으로 만들고 약한 장의 경우가 아닌 다른 모든 경우를 풀기 어렵게 만든다. 수치 상대성이론은 문제를 해결하고 분석하기 위해 일반상대성 이론의 한 분야로, 종종 슈퍼컴퓨터를 사용하여 블랙홀, 중력파, 중성자별 및 강한 장 체제(strong field regime)의 기타 현상을 연구한다.
에너지-운동량[편집]
특수 상대성이론에서 질량 에너지는 운동량과 밀접하게 연결되어 있다. 공간과 시간이 시공이라는 보다 포괄적인 실체의 다른 측면인 것처럼 질량-에너지와 운동량은 4-운동량이라고 하는 통일된 4차원 양의 다른 측면일 뿐이다. 결과적으로 질량-에너지가 중력의 근원이라면 운동량도 근원이 되어야 한다. 중력의 원천으로 운동량을 포함하면 이동하거나 회전하는 질량이 중력 자성으로 알려진 현상인 이동하는 전하에 의해 생성되는 자기장과 유사한 필드를 생성할 수 있다는 예측으로 이어진다.[62]

자기력은 움직이는 전하에 특수 상대성이론을 적용하여 추론할 수 있다는 것은 잘 알려져 있다. (이에 대한 설득력 있는 설명은 온라인에서 볼 수 있는 그의 물리학 강의 2권 chapter 13–6에서 파인만이 제시했다.[63]) 유사한 논리를 사용하여 중력자의 기원을 설명할 수 있다. 그림 5-7a에서 두 개의 평행하고 무한히 긴 거대한 입자의 흐름은 정지 상태에 있고 둘 사이의 중심에 있는 테스트 입자에 대해 동일하고 반대되는 속도 -v 및 +v를 갖는다. 설정의 대칭으로 인해, 중심 입자는 0이다. 속도가 단순히 덧셈이 되도록 를 가정한다. 그림 5-7b는 정확히 동일한 설정을 보여주지만 상위 흐름의 프레임에 있다. 테스트 입자의 속도는 +v이고 하단 흐름의 속도는 +2v이다. 물리적 상황은 바뀌지 않고 사물이 관찰되는 프레임뿐이므로 테스트 입자는 어느 쪽 흐름에도 끌리지 않아야 한다. 그러나 테스트 입자에 가해진 힘이 동일하다는 것은 전혀 분명하지 않다. (1) 바닥 흐름이 위쪽보다 빠르게 움직이기 때문에 아래쪽 흐름에 있는 각 입자는 위쪽에 있는 입자보다 더 큰 질량 에너지를 갖는다. (2) 로런츠 수축으로 인해 단위 길이당 입자가 위쪽 흐름보다 아래쪽 흐름에 더 많다. (3) 바닥 흐름의 활성 중력 질량에 대한 또 다른 기여는 이 시점에서 논의할 충분한 배경이 없는 추가 압력 항에서 비롯된다. 이러한 모든 효과는 함께 테스트 입자가 바닥 흐름을 향해 끌어당겨야 하는 것처럼 보인다.
테스트 입자는 바닥 흐름과 같은 방향으로 움직이는 입자를 밀어내는 역할을 하는 속도-의존성 힘 때문에 바닥 흐름으로 끌어당기지 않는다. 이 속도-의존성 중력 효과가 중력 자성이다.[3]:245–253
따라서 중력 자기장을 통해 움직이는 물질은 전자기 유도와 유사한 소위 틀 끌림(frame-dragging) 효과를 받는다. 이러한 중력자기력은 회전하는 초대질량 블랙홀에 의해 분출되는 상대론적 제트(그림 5-8) 생성의 기초가 된다고 제안되었다.[64][65]
압력과 응력[편집]
에너지 및 운동량과 직접적으로 관련된 양들은 중력의 소스들이어야 한다. 즉, 내부 압력 및 응력이다. 종합하면 질량-에너지, 운동량, 압력 및 응력은 모두 중력의 소스들로 작용한다. 집합적으로, 그것들은 시공간에 곡선을 그리는 방법을 알려주는 것이다.
일반 상대성이론은 압력이 질량-에너지 밀도와 정확히 동일한 강도를 갖는 중력 소스로 작용한다고 예측한다. 중력의 원천으로 압력을 포함시키면 일반 상대성이론과 뉴턴 중력의 예측 사이에 극적인 차이가 발생한다. 예를 들어, 압력 항은 중성자 별의 질량에 대한 최대 한계를 설정한다. 중성자별이 무거울수록 중력에 대항하여 무게를 지탱하기 위해 더 많은 압력이 필요하다. 그러나 증가된 압력은 별의 질량에 작용하는 중력을 증가시킨다. 톨만-오펜하이머-볼코프 한계에 의해 결정된 특정 질량 이상에서, 과정은 폭주하고 중성자별은 블랙홀로 붕괴된다.[3]:243,280
응력 항은 핵붕괴 초신성의 유체역학 시뮬레이션과 같은 계산을 수행할 때 매우 중요하다.[66]
시공간 곡률의 원인으로서 압력, 운동량 및 응력의 역할에 대한 이러한 예측은 우아하고 이론에서 중요한 역할을 한다. 압력과 관련하여 초기 우주는 복사가 지배적이었다.[67] 압력이 중력에 기여하지 않거나 질량-에너지만큼 중력의 근원과 같은 강도를 갖지 않는 경우 우주론적 데이터(예: 핵합성 존재비 등)를 재현할 수 있는 가능성은 매우 낮다. 마찬가지로, 응력 항이 중력의 원인으로 기여하지 않으면 아인슈타인 장 방정식의 수학적 일관성이 깨진다.
시공간 곡률의 소스들에 대한 실험적 테스트[편집]
정의들: 능동적, 수동적 및 관성 질량[편집]
본디Bondi는 질량의 가능한 다양한 유형들을 구별한다. (1) 능동적 질량()은 중력장의 소스로 작용하는 질량이다; (2) 수동적 질량()은 중력장에 반응하는 질량이다; (3) 관성 질량()은 가속도에 반응하는 질량이다.[68]
- 는 등가원리에 대한 토론의 중력 질량()과 동일하다.
뉴턴 이론에서는,
- 작용과 반작용의 제3법칙은 와 가 같아야한다는 것이다.
- 한편, 와 가 같은 것은 실험적 결과이다.
일반 상대성이론에서는,
- 와 의 등가성은 등가 원리에 의해 결정된다.
- 와 사이에 필요한 관계를 지시하는 "작용과 반작용" 원리는 없다.[68]
중력의 소스로서의 압력[편집]
중력의 소스(즉, 능동적 질량)의 강도를 측정하는 고전적인 실험은 1797년 헨리 캐번디시Henry Cavendish에 의해 처음 수행되었다(그림 5-9a). 작지만 조밀한 두 개의 공이 가는 철사에 매달려 비틀림 균형(Torsion balance)을 이룬다. 두 개의 큰 테스트 질량을 볼에 가깝게 가져오면 감지 가능한 토크가 발생한다. 장치의 치수와 비틀림 와이어의 측정 가능한 스프링 상수가 주어지면 중력 상수 G가 결정될 수 있다.
테스트 질량을 압축하여 압력 효과를 연구하는 것은 가망이 없다. 도달할 수 있는 실험실 압력이 금속 공의 질량-에너지에 비해 미미하기 때문이다.
그러나 원자핵 내부에서 양성자가 단단히 압착되어 생기는 반발 전자기 압력은 일반적으로 1028 atm ≈ 1033 Pa ≈ 1033 kg·s−2m−1. 이것은 약 1018kg/m3의 핵 질량 밀도의 약 1%에 해당한다(c2 ≈ 9×10 16m2s−2에서 인수분해한 후).[69]
만일 압력이 중력 소스로 작용하지 않는다면, 비율은 정전기 압력이 더 높은 원자 번호 Z가 더 높은 핵에서 더 낮아야 한다. L. B. 크로이저Kreuzer(1968)는 테플론과 동일한 부력 밀도를 갖는 액체 트리클로로에틸렌과 디브로모에탄dibromoethane의 혼합물에 매달린 테플론 질량을 사용하여 캐번디시 실험을 수행했다(그림 5-9b). 불소의 원자 번호는 Z = 9이고 브롬의 원자 번호는 Z = 35이다. 크로이저는 테플론 질량의 위치를 변경해도 토션 바의 차등 변형이 발생하지 않아 능동적 질량과 수동적 질량이 5×10−5의 정밀도로 동등하다는 것을 발견했다.[70]
크로이저는 원래 이 실험을 단순히 능동적 질량 대 수동적 질량의 비율 테스트로 간주했지만, 클리포드 윌Clifford Will(1976)은 이 실험을 중력장에 대한 소스의 결합의 기본 테스트로 재해석했다.[71]
1986년에, 바틀렛Bartlett와 반 뷰런Van Buren은 달 레이저 거리 측정실험이 달의 모양 중심과 질량 중심 사이의 2km 오프셋이 있음을 주목했다. 이것은 철(달의 핵에 풍부)과 알루미늄(지각과 맨틀에 풍부)의 분포가 비대칭임을 나타낸다. 압력이 질량-에너지만큼 시공간 곡률에 동등하게 기여하지 않는다면, 달은 고전 역학에서 예측한 궤도에 있지 않을 것이다. 그들은 능동적 질량과 수동적 질량 사이의 불일치에 대한 한계를 약 10-12까지 강화하기 위해 그들의 측정값을 사용했다.[72]
중력 자성[편집]
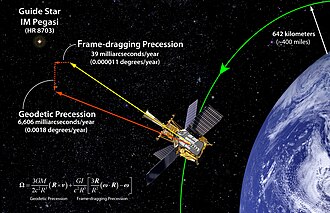
중력 자성의 존재는 2004년 4월 20일에 발사된 위성 기반 임무인 중력탐사기 B(Gravity Probe B)(GP-B)에 의해 입증되었다.[73] 우주 비행 단계는 2005년까지 지속되었다. 임무 목표는 중력 자성에 특히 중점을 두고 지구 근처의 시공간 곡률을 측정하는 것이었다.
초기 결과는 약 1%의 정확도로 상대적으로 큰 측지 효과(geodetic effect)(단순한 시공간 곡률로 인한 것이며 더시터르 세차 운동이라고도 함)를 확인했다. 훨씬 작은 틀 끌림 효과(중력 자기로 인한 것으로 렌세-티링 세차 운동(Lense–Thirring precession)이라고도 함)는 자이로스코프에서 가변 드리프트를 유발하는 예기치 않은 전하 효과로 인해 측정하기 어려웠다. 그럼에도 불구하고 2008년 8월까지 틀 끌림 효과는 예상 결과의 15% 이내로 확인되었으며[74] 측지 효과는 0.5% 이상으로 확인되었다.[75][76]
레이저 상대성 위성(LARES), 레이저 지구역학 위성(LAGEOS)-1 및 LAGEOS-2 위성의 레이저 거리 관측에 의한 틀 끌림의 후속 측정은 GP-B 측정에서 개선되었으며 결과(2016년 기준)는 이 결과의 정확성에 대해 약간의 불일치가 있었지만,[77] 이론값의 5% 이내로 효과를 입증했다.[78]
또 다른 노력인 일반 상대성이론의 자이로스코프(GINGER) 실험은 이 효과를 측정하기 위해 지표면 아래 1400m 아래에서 서로 직각으로 장착된 3개의 6m 링 레이저(ling laser)를 사용하려고 한다.[79][80]
기술적 주제[편집]
시공간은 실제로 휘었는가?[편집]
푸앵카레의 규약주의자 관점들에서는, 유클리드 기하학과 비유클리드 기하학을 선택해야 하는 필수 기준은 경제성과 단순성이다. 실재론자들은 아인슈타인이 시공간이 비유클리드적이라는 것을 발견했다고 말할 것이다. 규약주의자는 아인슈타인이 비유클리드 기하학을 사용하는 것이 더 편리하다는 것을 알았다고 말할 것이다. 규약주의자는 아인슈타인의 분석이 시공간의 기하학이 실제로 무엇인가에 대해 아무 말도 하지 않았다고 주장할 것이다.[81]
그런 말을 하면,
- 1. 일반 상대성이론을 평평한 시공간으로 나타낼 수 있는가?
- 2. 일반 상대성이론에 대한 평평한 시공간 해석이 일반적인 곡선 시공간 해석보다 더 편리한 상황이 있는가?
첫 번째 질문에 대한 응답으로 데저Deser, 그리슈크Grishchuk, 로젠Rosen, 와인버그 등을 포함한 많은 저자들은 평평한 다양체의 장으로 중력의 다양한 공식들을 제공했다. 이러한 이론은 "바이메트릭 중력(bimetric gravity)", "일반 상대성이론에 대한 장 이론적 접근" 등으로 다양하게 불린다.[82][83][84][85] 킵 손은 이러한 이론에 대한 한 대중적 리뷰를 제공했다.[86]:397–403
평평한 시공간 패러다임은 물질이 중력장을 생성하여 자를 원주 방향에서 방사형으로 돌릴 때 자를 수축시키고 시계의 똑딱거리는 속도를 팽창시킨다고 가정한다. 평평한 시공간 패러다임은 둘 다 동일한 물리적 현상을 나타낸다는 점에서 휘어진 시공간 패러다임과 완전히 동일하다. 그러나 그들의 수학적 공식은 완전히 다르다. 연구하는 물리학자들은 문제의 요구 사항에 따라 휘어진 및 평평한 시공간 기술 사용하기를 일상적으로 전환한다. 평평한 시공간 패러다임은 약한 장에서 근사 계산을 수행할 때 특히 편리한 것으로 판명되었다. 따라서 중력파 문제를 풀 때는 평평한 시공간 기술이 사용되는 반면에, 블랙홀 분석에는 휘어진 시공간 기술이 사용되는 경향이 있다.[86]:397–403
점근적 대칭들[편집]
특수 상대성이론의 시공간 대칭 군은 3개의 로런츠 부스트, 3개의 회전 및 4개의 시공간 병진으로 구성된 10차원 군인 푸앵카레 군이다. 일반 상대성이론에 어떤 대칭이 적용될 수 있는지 묻는 것이 논리적이다. 다루기 쉬운 경우는 중력장의 모든 근원에서 멀리 떨어진 관찰자에게 보이는 시공간의 대칭을 고려하는 것일 수 있다. 점근적으로 평평한 시공간 대칭에 대한 순진한 기대는 단순히 특수 상대성이론, 즉 푸앵카레 군의 평평한 시공간 대칭을 확장하고 재생산하는 것일 수 있다.
1962년 헤르만 본디Hermann Bondi, M. G. 반 데르 부르그van der Burg, A. W. 메츠너Metzner[87] 및 레이너 K. 삭스Rainer K. Sachs[88]는 전파되는 중력파로 인한 무한대의 에너지 흐름을 조사하기 위해 이 점근 대칭 문제를 다루었다. 그들의 첫 번째 단계는 중력장에 빛과 같은 무한대를 배치할 물리적으로 합리적인 경계 조건을 결정하여 점근 대칭군의 본성에 대한 선험적 가정을 하지 않고-그러한 군이 존재한다는 가정조차 하지 않고, 계량이 점근적으로 평평하다고 말하는 것이 무엇을 의미하는지 특성화하는 것이다. 그런 다음 가장 합리적인 경계 조건으로 간주되는 것을 설계한 후, 점근적으로 평평한 중력장에 적합한 경계 조건의 형태를 불변으로 남겨두는 점근 대칭 변환 결과의 특성을 조사했다. 그들이 발견한 것은 점근 대칭 변환이 실제로 한 군을 형성하며, 이 군의 구조가 여태까지 존재하는 특정 중력장에 의존하지 않는다는 것이다. 이것은 예상대로 적어도 공간적 무한대에서 중력장의 역학에서 시공간의 운동학을 분리할 수 있음을 의미한다. 1962년에 수수께끼처럼 놀랍게도 BMS 군의 하위 군인 유한 차원 푸앵카레 군 대신 점근 대칭 군으로 풍부한 무한 차원 군(소위 BMS 군)을 발견했다. 로런츠 변환은 점근 대칭 변환일 뿐만 아니라, 로런츠 변환은 아니자만 점근 대칭 변환인 추가 변환도 있다. 사실, 그들은 초병진(supertranslation)들로 알려진 무한대 변환 생성기를 추가로 발견했다. 이것은 일반 상대성이론(GR)이 장거리에서 약한 장의 경우에는 특수 상대성이론으로 축소되지 않는다는 결론을 의미한다.[89]:35
리만 기하학[편집]
- 이 섹션은 리만 기하학에서 발췌 한 내용입니다.
리만 기하학은 리만 다양체를 연구하는 미분 기하학의 한 분야로, 리만 계량 (점에서 점으로 매끄럽게 변하는 접공간에서의 한 내적)을 가진 한 매끄러운 다양체들로 정의된다. 특히 각도, 곡선의 길이(length of curves), 표면적 및 부피에 대한 국소적인 개념을 제공함다. 그것들로부터, 국소 기여도들를 적분하여 일부 다른 대역 량들을 도출될 수 있다.
리만 기하학은 베른하르트 리만의 취임 강연 "Ueber die Hypothesen, welche der Geometrie zu Grunde liegen" ("기하학의 기초가 되는 가설에 대하여")에서 표현된 비전에서 시작되었다.[90] 이는 R3에서 표면의 미분 기하학(differential geometry of surfaces)을 매우 광범위하고 추상적으로 일반화 한 것입니다. 리만 기하학의 발전은 고차원의 [[w: Differentiable manifold |미분가능 다양체(differentiable manifold)]] 연구에 적용할 수 있는 기법과 함께 표면의 기하학 및 거기에서의 측지선의 거동에 관한 다양한 결과들을 통합하는 결과를 가져왔다. 아인슈타인의 일반 상대성이론의 공식화를 가능하게 했고, 해석학뿐만 아니라 군론과 표현론에 지대한 영향을 미쳤고, 대수 및 미분 위상수학의 발전에 박차를 가했다.
휘어진 다양체들[편집]
물리적인 이유로, 시공간 연속체는 수학적으로 한 4차원의, 매끄럽고, 연결된 로런츠 다양체 로 정의된다. 이것은 매끄러운 로런츠 계량 는 의 계량 부호수를 가진다. 이 계량은 입자 및 광선의 측지선을 결정할 뿐만 아니라 시공간의 기하학을 결정한다. 이 다양체의 각 점(사건)에 대해 좌표 차트(coordinate chart)는 기준 프레임에서 관찰자를 나타내는 데 사용된다. 일반적으로 데카르트 좌표 가 사용된다. 또한, 단순성을 위해 측정 단위는 일반적으로 광속 가 1이 되도록 선택된다.[91]
기준 프레임(관찰자)는 이러한 좌표 차트 중 하나로 식별할 수 있다. 그러한 관찰자는 모든 사건 를 설명할 수 있다. 다른 기준 프레임은 에 대한 두 번째 좌표 차트로 식별할 수 있다. 두 명의 관찰자(각 기준 프레임에 하나씩)가 동일한 사건 를 설명하지만 다른 설명을 얻을 수 있다.[91]
일반적으로, 한 다양체를 커버하려면 겹치는 좌표 차트들이 많이 필요하다. 두 개의 좌표 차트들이 주어지면 하나는 다음을 포함한다: (한 관찰자를 나타냄) 및 다음을 포함하는 다른 것 (다른 관찰자를 나타냄), 차트들의 교집합은 두 관찰자가 물리량을 측정하여 결과를 비교할 수 있는 시공간의 영역을 나타낸다. 두 측정 세트 간의 관계는 이 교집합에 대한 정칙(non-singular) 좌표 변환에 의해 제공된다. 주변에서 측정을 수행할 수 있는 국소 관찰자로서의 좌표 차트의 아이디어는 실제로 물리적 데이터를 국소적으로 수집하는 방법으로 볼 수 있기 때문에 물리적으로 타당하다.[91]
예를 들어, 한 명은 지구에 있고 다른 한 명은 목성으로 가는 고속 로켓을 타고 있는 두 명의 관찰자들은 목성에 충돌하는 혜성을 관찰할 수 있다(이것은 사건 이다) 일반적으로, 그들은 이 충돌의 정확한 위치와 시기에 대해 동의하지 않을 것이니, 즉, (다른 좌표계를 사용하기 때문에) 서로 다른 4-튜플 를 가질 것이다. 운동학적 설명들은 다르지만 운동량 보존 및 열역학 제1법칙과 같은 동적(물리적) 법칙은 여전히 유효하다. 사실, 상대성이론은 이러한(그리고 모든 다른 물리적) 법칙이 모든 좌표계에서 동일한 형태를 취해야 한다고 규정한다는 점에서 이보다 더 많은 것을 요구한다. 이것은 상대성이론에 모든 물리적 량들이 표현되는 텐서들을 도입한다.
만일 그 측지선의 한 점에 대한 접선 벡터가 이 성질을 갖는 경우, 측지선은 시간꼴, 널 또는 공간꼴이라고 말한다. 시공간에서의 입자들과 광선들의 경로들은 각각 시간꼴 측지선과 널(빛꼴) 측지선들로써 표시된다.[91]
3+1 시공간의 특권적 특성[편집]
- 이 섹션은 인류 원리 § 시공간(Anthropic principle § Dimensions of spacetime)으로부터의 한 발췌이다.
시공간의 차원에는 두 종류의 차원이 있다: 공간적(양방향) 그리고 시간적(일방향)의 두 가지 종류가 있다.[93] 장소를 나타내는 차원의 수를 N으로 하고 또한 시간을 나타내는 차원의 수는 T로 하자. N = 3 및 T = 1이라는 것은, 끈 이론에 의해 호출되고 또한 현재까지 감지 할 수 없는 축소화된 차원들을 제쳐두고, N이 3과 다르고 T가 1과 다를 때의 물리적 결과에 호소함으로써 설명될 수 있다. 이 주장은 종종 인류적인 성격이며 또한 완전한 개념이 유행하기 전이지만 아마도 최초의 종류 일 수 있다.
우주의 차원이 특별하다는 암묵적인 개념은 먼저 고트프리트 빌헬름 라이프니츠가 형이상학 서설에서 세계가 "가설에서 가장 단순하고 현상에서 가장 풍부한 것"이라고 제안한 것에 기인한다.[94] 이마누엘 칸트는 3차원 공간이 만유인력의 법칙의 역제곱의 결과라고 주장했다. 칸트의 주장은 역사적으로 중요하지만, 존 D. 바로우John D. Barrow는 "펀치 라인을 다시 전면으로 가져온다: 우리가 자연에서 역제곱 법칙을 보는 이유를 설명하는 것은 공간의 3차원성이며, 그 반대의 경우는 아니다."라고 말했다. (Barrow 2002: 204).[노트 16]
1920년에, 파울 에렌페스트는 만일 시간 차원이 단 하나이고 공간 차원이 3차원보다 크면, 태양 주위의 행성의 궤도가 안정적으로 유지될 수 없음을 보여주었다. 은하의 중심을 도는 별의 궤도도 마찬가지다.[95] 에렌페스트는 또한 만일 공간 차원들이 어떤 짝수이면, 파동 충격량의 다른 부분들이 다른 속도로 이동할 것임을 보여주었다. 만일 k가 양의 정수인 공간 차원이 있다면, 파동 충격량이 왜곡된다. 1922년 헤르만 바일은 전자기학의 맥스웰의 이론이 한 사차원 다양체에 대해서만 작용으로 표현할 수 있다고 주장했다..[96] 마지막으로 탕헤리니Tangherlini는 1963년에 공간 차원이 3차원 이상일 때, 핵 주위의 전자 궤도들이 안정적일 수 없어서; 전자들이 핵속으로 떨어지거나 또는 흩어질 것을 보여주었다.[97]
막스 테그마크Max Tegmark는 다음과 같은 인류적인 방식으로 앞의 주장을 확장한다.[98] 만일 T가 1과 다르면, 물리적 시스템의 거동이 관련 편미분 방정식의 지식으로부터 안정적으로 예측될 수 없다. 그러한 한 우주에서는, 기술을 조작할 수 있는 지적 생명체가 출현할 수 없다. 또한 만일 T > 1이면, 테그마크는 양성자들과 전자들이 불안정하여 자신보다 더 큰 질량을 갖는 입자들로 붕괴될 수 있다고 주장한다. (만일 입자의 온도가 충분히 낮으면 이것은 어떤 문제는 아니다.)[98] 마지막으로, 만일 N < 3이면, 모든 종류의 중력은 문제가 되고, 또한 그 우주는 관찰자들을 포함하기에는 너무 단순할 것다. 예를 들어, N < 3일 때는, 신경들이 교차하지 않고는 지나갈 수 없다.[98] 따라서 인류적 및 다른 주장들은 우리 주변의 세계를 기술하는 N = 3 및 T = 1을 제외한 모든 경우들을 배제한다.
반면에, 이상적인 단원자 기체가 자체 중력 하에서 블랙홀을 생성한다는 점에서 웨이샹펑Wei-Xiang Feng은 (3+1) 차원의 시공간이 중요하지 않은 차원성임을 보여주었다. 게다가, 그것은 한 "양의" 우주 상수를 가진 어떤 "안정된" 가스권을 감당할 수 있는 것은 독특한 차원성이다. 그러나 자기-중력 기체는 관찰된 우주 상수의 작은 양성으로 인해 질량 구체가 ~1021 태양 질량보다 크면 안정적으로 결합할 수 없다.[99]
2019년 제임스 스카길James Scargill은 복잡한 생명체가 두 개의 공간적 차원과 함께 할 수도 있다고 주장했다. 스카길에 따르면, 중력에 대한 한 순수한 스칼라 이론은 어떤 국소적인 중력적 힘을 가능하게 할 수 있으며, 또한 2D 네트워크들은 복잡한 신경 네트워크들을 위해서 충분할 수 있다.[100][101]
같이 보기[편집]
- 일반상대론의 수학적 공식화 개론
- 복소 시공간
- 아인슈타인의 사고 실험(Einstein's thought experiments)
- 사차원주의
- 지리학
- 대역적 시공간 구조(Global spacetime structure)
- 시공간의 목록(List of spacetimes)
- 거리 공간
- 시간과 공간의 철학
- 현재
- 시간 지리학(Time geography)
노트[편집]
- ↑ 라틴어 루멘(lumen)로부터 luminiferous, 빛, + ferens, 나르는; 그리스어 αἰθήρ(aithēr)로부터 에테르, 순수한 공기, 맑은 하늘
- ↑ 동시성은 관습의 문제라고 말함으로써, 푸앵카레는 시간에 대해 이야기하려면 동기화된 시계가 있어야 하고 시계의 동기화는 지정된 작동 절차(관례)에 의해 설정되어야 함을 의미했다. 이러한 입장은 당시의 부정확한 시계의 작동과 무관한 절대적이고 진정한 시간을 생각했던 뉴턴과의 근본적인 철학적 단절을 나타낸다. 이 입장은 또한 시간, 동시성 및 지속성이 직관적 이해의 문제라고 주장한 영향력 있는 철학자 앙리 베르그송에 대한 직접적인 공격을 나타낸다.
- ↑ 푸앵카레가 채택한 작동 절차는 아인슈타인 동기화(Einstein synchronisation)로 알려진 절차와 본질적으로 동일했지만, 19세기 중반에 전신 기사에 의해 이미 널리 사용된 절차였다. 기본적으로 두 개의 시계를 동기화하려면 하나에서 다른 시계으로 광 신호를 깜박이고 플래시가 도달하는 데 걸리는 시간을 조정한다.
- ↑ 실제로 아인슈타인 경력의 특징은 물리적 문제를 이해하기 위한 기본 도구로 시각화된 사고 실험(Gedanken-Experimente)을 사용한 것이다. 특수 상대성이론을 위해 그는 움직이는 기차와 번쩍이는 번개를 사용하여 가장 날카로운 통찰력을 얻었다. 곡선 시공간에 대해 그는 지붕에서 떨어지는 화가, 가속 엘리베이터, 곡선 표면을 기어 다니는 눈이 먼 딱정벌레 등을 고려했다. 실재의 본성에 관한 보어와의 위대한 솔베이 토론(1927, 1930)에서 그는 하이젠베르크의 불확정성 원리를 회피할 수 있는 수단을 최소한 개념적으로 보여주기 위해 여러 가상 장치를 고안했다. 마지막으로, 양자 역학에 대한 문헌에 대한 지대한 공헌에서 아인슈타인은 양자 얽힘으로 알려진 현상을 예상하면서 두 입자가 잠시 상호 작용한 다음 떨어져서 상태가 상호 관련되도록 고려했다.
- ↑ 이 강의의 원래 버전에서 민코프스키는 에테르와 같은 구식 용어를 계속 사용했지만 이 강의의 사후 간행물은 1915년 《Annals of Physics(Annalen der Physik)》에서 조머펠트에 의해 편집되어 이 용어를 제거했다. 조머펠트는 또한 아인슈타인에 대한 민코프스키의 판단을 상대성 원리의 단순한 설명자에서 주요 설명자로 수정하기 위해 이 강의의 출판된 형식을 편집했다.
- ↑ (다음에서 군 G∞는 갈릴레이 군이고 군 Gc는 로런츠 군이다.) "이와 관련하여 c = ∞ 에 대한 극한에서 군Gc, 즉 군 G∞가 정확히 뉴톤 역학에 속하는 전체 군이된다는 것은 명확하다. 이러한 상황에서 Gc가 G∞보다 수학적으로 더 이해하기 쉬우므로 수학자는 군 G∞가 아니라 군 Gc에 대해서 자유로운 상상을 통해 자연 현상이 실제로 불변성을 가지고 있다는 생각을 하게 될 수 있다. 여기서 c는 확실히 유한하며 일반 측정 단위를 사용하면 매우 크다."
- ↑ 예를 들어, 로런츠 군은 4차원의 등각군(conformal group)의 부분군이다. 로런츠 군은 평면을 평면으로 변환하는 라구에레 군(Laguerre group)과 동형isomorphic이며, 그것은 평면의 뫼비우스 군과 동형이며, 쌍곡선 모형(hyperboloid model)으로 종종 표현되는 쌍곡공간의 등형 군과 동형이다.
- ↑ 데카르트 평면에서 일반 회전은 원을 변경하지 않은 상태로 유지한다. 시공간에서 쌍곡선 회전은 쌍곡선 메트릭(hyperbolic metric)을 유지한다.
- ↑ 가속(감속)이 없더라도, 즉 일정한 고속 외부 여행을 위해 하나의 관성계 O를 사용하고 일정하고 고속 내부 여행을 위해 다른 관성계 I를 사용하더라도 이러한 계들(O 및 I)에서 경과 시간의 합은 다음과 같다. 정지 관성계 S의 경과 시간보다 짧다. 따라서 가감속은 외부 및 내부 여행 동안 경과 시간이 짧은 원인이 아니다. 대신 외부 및 내부 여행에 대해 두 개의 서로 다른 일정한 고속 관성계를 사용하는 것이 실제로 총 경과 시간이 더 짧은 원인이다. 물론, 같은 쌍둥이가 여정의 바깥쪽과 안쪽 다리를 여행하고 여행의 바깥쪽에서 안쪽 다리로 안전하게 전환해야 하는 경우 가속과 감속이 필요하다. 여행하는 쌍둥이가 고속 외부 관성계를 타고 즉시 고속 내부 관성계로 전환할 수 있다면 예제는 여전히 작동할 것이다. 요점은 그 진짜 이유를 분명히 밝혀야 한다는 것이다. 비대칭은 두 개의 다른 관성계(O 및 I)의 경과 시간 합을 단일 관성계 S의 경과 시간과 비교하기 때문이다.
- ↑ 상대론적 시나리오 분석의 용이성은 종종 분석을 수행하기로 선택한 프레임에 따라 다르다. 이 링크된 이미지에서 소스와 수신기가 서로 가장 가깝게 접근하는 가로 도플러 이동 시나리오의 대안 보기를 제시한다. (a) 수신기의 계에서 시나리오를 분석하면 분석이 예상보다 더 복잡하다는 것을 알 수 있다. 천체의 겉보기 위치는 빛이 관찰자에게 도달하는 동안 물체의 움직임으로 인해 실제 위치(또는 기하학적 위치)에서 옮겨진다. 소스는 수신기에 대해 상대적으로 시간 팽장되지만 이 시간 팽장에 의해 암시된 적색 편이는 수신기와 소스의 겉보기 위치 사이의 상대 운동의 세로 구성 요소로 인해 파란색 편이에 의해 상쇄된다. (b) 대신 소스 계에서 시나리오를 분석하면 훨씬 쉽다. 소스에 위치한 관찰자는 문제 설명을 통해 수신기가 자신과 가장 가까운 지점에 있다는 것을 알고 있다. 이는 수신기에 분석을 복잡하게 만드는 종방향 모션 요소가 없음을 의미한다. 수신기의 시계는 소스에 비해 시간 팽창하기 때문에 수신기가 받는 빛은 따라서 감마 계수만큼 파란색으로 이동한다.
- ↑ 모든 실험이 적색편이 측면에서 효과를 특징짓는 것은 아니다. 예를 들어, 쿤디그 실험(Kündig experiment)은 원심분리기 로터의 중심에 설치된 뫼스바우어Mössbauer 소스 설정과 림에 있는 흡수기를 사용하여 횡방향 청색편이를 측정하기 위해 설정되었다.
- ↑ 신속도는 자연스럽게 로런츠 그룹의 리 대수 내에서 순수 부스트 생성기의 좌표로 발생한다. 마찬가지로, 회전 각도는 리 대수에서 순수 회전 생성기의 좌표(모듈로 2π)로 자연스럽게 발생한다. (그들은 함께 전체 리 대수학을 좌표화한다.) 주목할 만한 차이점은 회전 각도에서 회전은 주기적인 반면, 가속도는 주기적인 것이 아니라 일대일이라는 것이다. 부스트와 회전의 유사성은 형식적인 유사성이다.
- ↑ 상대성 이론에서 적절한 가속도는 물리적 가속도(즉, 물체가 경험하는 가속도계와 같은 측정 가능한 가속도)이다. 따라서 자유 낙하에 대한 가속도 또는 측정 대상에 대해 잠시 정지한 관성 관찰자이다.
- ↑ 뉴턴 자신도 이러한 가정에 내재된 어려움을 날카롭게 인식하고 있었지만, 실제적인 문제로서 이러한 가정을 하는 것만이 그가 진보할 수 있는 유일한 방법이었다. 1692년, 그는 그의 친구 리처드 벤틀리에게 다음과 같이 썼다: "중력은 물질에 선천적이고 내재적이며 필수적이어야 한다. 그래서 한 물체가 진공의 매개 없이 다른 물체를 통해 다른 물체에게 행동할 수 있고, 그들의 행동과 힘이 다른 물체에게 전달될 수 있다.철학적 문제에 있어서 유능한 사고력을 가진 사람은 결코 그것에 빠질 수 없다.
- ↑ 더 정확하게 말하면 중력장은 자체적으로 결합된다. 뉴턴 중력에서 두 점 질량으로 인한 포텐셜은 단순히 두 질량의 포텐셜의 합이지만 일반 상대성에는 적용되지 않는다. 이것은 등가 원리의 결과로 생각할 수 있다. 중력이 자체적으로 결합하지 않으면 상호 중력 인력에 의해 결합된 두 입자는 중력 질량과 동일한 관성 질량(음의 결합 에너지로 인해)을 갖지 않을 것이다.
- ↑ 이것은 중력의 법칙(또는 다른 역제곱 법칙)이 플럭스의 개념과 플럭스 밀도와 필드 강도의 비례 관계에서 따르기 때문이다. N = 3이면 3차원 입체 물체는 선택한 공간 차원에서 크기의 제곱에 비례하는 표면적을 갖는다. 특히, 반지름 r인 구의 면적은 4πr2이다. 보다 일반적으로 N 차원의 공간에서 r의 거리만큼 떨어진 두 물체 사이의 중력의 세기는 rN−1에 반비례한다.
추가적 상세[편집]
- ↑ 이 그림에 제시된 시나리오를 보는 다른 리포터들은 상황에 대한 그들의 지식에 따라 시나리오를 다르게 해석한다. (i) 제1 리포터는, 입자 2 및 3의 질량 중심에서, 그러나 큰 질량 1을 알지 못하는, 시나리오 A의 입자 사이에 반발력이 존재하는 반면, 시나리오 B의 입자 사이에 인력의 힘이 존재한다고 결론짓는다. (ii) 큰 질량 1을 의식한 제2 리포터는, 제1 리포터의 순진한 태도에 미소짓는다. 이 두 번째 기자는 실제로 입자 2와 3 사이의 명백한 힘이 질량 1에 의한 미분 인력으로 인한 조석 효과를 나타낸다는 것을 알고 있다. (iii) 일반 상대성 이론 훈련을 받은 세 번째 기자는 사실 세 물체 사이에 작용하는 힘이 전혀 없다는 것을 알고 있다. 오히려 세 물체 모두 시공간에서 측지선을 따라 움직인다.
각주[편집]
- ↑ Rynasiewicz, Robert. "Newton's Views on Space, Time, and Motion". Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. Retrieved 24 March 2017.
- ↑ Davis, Philip J. (2006). Mathematics & Common Sense: A Case of Creative Tension. Wellesley, Massachusetts: A.K. Peters. p. 86.
- ↑ 가 나 다 라 마 바 사 아 자 차 카 타 파 하 거 너 더 러 머 버 Schutz, Bernard (2004). 《Gravity from the Ground Up: An Introductory Guide to Gravity and General Relativity》 (영어) Reprint판. Cambridge: Cambridge University Press. ISBN 0-521-45506-5. 2017년 5월 24일에 확인함.
- ↑ Fock, V. (1966). The Theory of Space, Time and Gravitation (2nd ed.). New York: Pergamon Press Ltd. p. 33.
- ↑ Lawden, D. F. (1982). Introduction to Tensor Calculus, Relativity and Cosmology (3rd ed.). Mineola, New York: Dover Publications. p. 7.
- ↑ 가 나 다 라 마 Collier, Peter (2017). A Most Incomprehensible Thing: Notes Towards a Very Gentle Introduction to the Mathematics of Relativity (3rd ed.). Incomprehensible Books.
- ↑ Rowland, Todd. "Manifold". Wolfram Mathworld. Wolfram Research. Retrieved 24 March 2017.
- ↑ 가 나 French, A.P. (1968). Special Relativity. Boca Raton, Florida: CRC Press. pp. 35–60.
- ↑ 가 나 다 라 마 바 사 Taylor, Edwin F.; Wheeler, John Archibald (1992). Spacetime Physics: Introduction to Special Relativity (2nd ed.). San Francisco: Freeman.
- ↑ Scherr, Rachel E.; Shaffer, Peter S.; Vokos, Stamatis (July 2001). "Student understanding of time in special relativity: Simultaneity and reference frames" (PDF). American Journal of Physics. 69 (S1): S24–S35.
- ↑ Hughes, Stefan (2013). Catchers of the Light: Catching Space: Origins, Lunar, Solar, Solar System and Deep Space. Paphos, Cyprus: ArtDeCiel Publishing. pp. 202–233.
- ↑ Williams, Matt (28 January 2022). "What is Einstein's Theory of Relativity?". Universe Today.
- ↑ Stachel, John (2005). "Fresnel's (Dragging) Coefficient as a Challenge to 19th Century Optics of Moving Bodies." (PDF). In Kox, A. J.; Eisenstaedt, Jean (eds.). The Universe of General Relativity. Boston: Birkhäuser. pp. 1–13.
- ↑ "George Francis FitzGerald". The Linda Hall Library. Retrieved 13 August 2022.
- ↑ "The Nobel Prize in Physics 1902". NobelPrize.org. Retrieved 13 August 2022.
- ↑ 가 나 다 Pais, Abraham (1982). "Subtle is the Lord–": The Science and the Life of Albert Einstein (11th ed.). Oxford: Oxford University Press.
- ↑ Darrigol, O. (2005), "The Genesis of the theory of relativity" (PDF), Séminaire Poincaré, 1: 1–22,
- ↑ Miller, Arthur I. (1998). Albert Einstein's Special Theory of Relativity. New York: Springer-Verlag.
- ↑ Galison, Peter (2003). Einstein's Clocks, Poincaré's Maps: Empires of Time. New York: W. W. Norton & Company, Inc. pp. 13–47.
- ↑ Poincare, Henri (1906). "On the Dynamics of the Electron (Sur la dynamique de l'électron)". Rendiconti del Circolo Matematico di Palermo. 21: 129–176. Bibcode:1906RCMP...21..129P.
- ↑ Zahar, Elie (1989) [1983], "Poincaré's Independent Discovery of the relativity principle", Einstein's Revolution: A Study in Heuristic, Chicago: Open Court Publishing Company,
- ↑ 가 나 Walter, Scott A. (2007). "Breaking in the 4-vectors: the four-dimensional movement in gravitation, 1905–1910". In Renn, Jürgen; Schemmel, Matthias (eds.). The Genesis of General Relativity, Volume 3. Berlin: Springer. pp. 193–252.
- ↑ Einstein, Albert (1905). "On the Electrodynamics of Moving Bodies ( Zur Elektrodynamik bewegter Körper)". Annalen der Physik. 322 (10): 891–921. Bibcode:1905AnP...322..891E.
- ↑ Isaacson, Walter (2007). Einstein: His Life and Universe. Simon & Schuster. pp. 26–27, 122–127, 145–146, 345–349, 448–460.
- ↑ 가 나 Weinstein, Galina (2012). "Max Born, Albert Einstein and Hermann Minkowski's Space–Time Formalism of Special Relativity". arXiv:1210.6929
- ↑ Galison, Peter Louis (1979). "Minkowski's space–time: From visual thinking to the absolute world". Historical Studies in the Physical Sciences. 10: 85–121. doi:10.2307/27757388.
- ↑ 가 나 Minkowski, Hermann (1909). "Raum und Zeit" [Space and Time]. Jahresbericht der Deutschen Mathematiker-Vereinigung. B.G. Teubner: 1–14.
- ↑ Close [28] Cartan, É.; Fano, G. (1955) [1915]. "La théorie des groupes continus et la géométrie". Encyclopédie des Sciences Mathématiques Pures et Appliquées. 3 (1): 39–43. (Only pages 1–21 were published in 1915, the entire article including pp. 39–43 concerning the groups of Laguerre and Lorentz was posthumously published in 1955 in Cartan's collected papers, and was reprinted in the Encyclopédie in 1991.)
- ↑ Kastrup, H. A. (2008). "On the advancements of conformal transformations and their associated symmetries in geometry and theoretical physics". Annalen der Physik. 520 (9–10): 631–690. arXiv:0808.2730.
- ↑ Ratcliffe, J. G. (1994). "Hyperbolic geometry". Foundations of Hyperbolic Manifolds. New York. pp. 56–104.
- ↑ 가 나 다 Kogut, John B. (2001). Introduction to Relativity. Massachusetts: Harcourt/Academic Press.
- ↑ D'Inverno, Ray (1992). Introducing Einstein's Relativity. New York: Oxford University Press.
- ↑ Landau, L. D. Lifshitz E,M. (2013). The classical theory of fields (Vol. 2).
- ↑ Carroll, Sean (2022). The Biggest Ideas in the Universe. New York: Penguin Random House LLC. pp. 155–156.
- ↑ Curiel, Erik; Bokulich, Peter. "Lightcones and Causal Structure". Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. Retrieved 26 March 2017.
- ↑ Savitt, Steven. "Being and Becoming in Modern Physics. 3. The Special Theory of Relativity". The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. Retrieved 26 March 2017.
- ↑ 가 나 다 라 마 바 Schutz, Bernard F. (1985). A first course in general relativity. Cambridge, UK: Cambridge University Press. p. 26.
- ↑ 가 나 다 라 마 바 사 Weiss, Michael. "The Twin Paradox". The Physics and Relativity FAQ. Retrieved 10 April 2017.
- ↑ Mould, Richard A. (1994). Basic Relativity (1st ed.). Springer. p. 42.
- ↑ Lerner, Lawrence S. (1997). Physics for Scientists and Engineers, Volume 2 (1st ed.). Jones & Bartlett Pub. p. 1047.
- ↑ 가 나 다 라 마 바 사 아 자 차 카 타 파 하 거 Bais, Sander (2007). Very Special Relativity: An Illustrated Guide. Cambridge, Massachusetts: Harvard University Press.
- ↑ Forshaw, Jeffrey; Smith, Gavin (2014). Dynamics and Relativity. John Wiley & Sons. p. 118.
- ↑ 가 나 다 라 마 바 사 아 자 차 카 타 파 하 거 너 더 Morin, David (2017). Special Relativity for the Enthusiastic Beginner. CreateSpace Independent Publishing Platform.
- ↑ Landau, L. D.; Lifshitz, E. M. (2006). The Classical Theory of Fields, Course of Theoretical Physics, Volume 2 (4th ed.). Amsterdam: Elsevier. pp. 1–24.
- ↑ 가 나 Morin, David (2008). Introduction to Classicaㅣ Mechanics: With Problems and Solutions. Cambridge University Press.
- ↑ Rose, H. H. (21 April 2008). "Optics of high-performance electron microscopes". Science and Technology of Advanced Materials. 9 (1): 014107.
- ↑ Griffiths, David J. (2013). Revolutions in Twentieth-Century Physics. Cambridge: Cambridge University Press. p. 60.
- ↑ Byers, Nina (1998). “E. 대칭과 보존 법칙 사이의 깊은 연결에 대한 Noether의 발견”. arXiv:physics/9807044.
- ↑ Nave, R. "Energetics of Charged Pion Decay". Hyperphysics. Department of Physics and Astronomy, Georgia State University
- ↑ Thomas, George B.; Weir, Maurice D.; Hass, Joel; Giordano, Frank R. (2008). Thomas' Calculus: Early Transcendentals (Eleventh ed.). Boston: Pearson Education, Inc. p. 533.
- ↑ Taylor, Edwin F.; Wheeler, John Archibald (1992). Spacetime Physics (2nd ed.). W. H. Freeman.
- ↑ 가 나 Gibbs, Philip. "Can Special Relativity Handle Acceleration?". The Physics and Relativity FAQ. math.ucr.edu. Retrieved 28 May 2017.
- ↑ Franklin, Jerrold (2010). "Lorentz contraction, Bell's spaceships, and rigid body motion in special relativity". European Journal of Physics. 31 (2): 291–298. arXiv:0906.1919
- ↑ Lorentz, H. A.; Einstein, A.; Minkowski, H.; Weyl, H. (1952). The Principle of Relativity: A Collection of Original Memoirs on the Special and General Theory of Relativity. Dover Publications.
- ↑ 가 나 다 Mook, Delo E.; Vargish, Thoma s (1987). Inside Relativity. Princeton, New Jersey: Princeton University Press.
- ↑ Mester, John. "Experimental Tests of General Relativity" (PDF). Laboratoire Univers et Théories. Archived from the original (PDF) on 18 March 2017.
- ↑ 가 나 Carroll, Sean M. (2 December 1997). "Lecture Notes on General Relativity". arXiv:gr-qc/9712019.
- ↑ Le Verrier, Urbain (1859). "Lettre de M. Le Verrier à M. Faye sur la théorie de Mercure et sur le mouvement du périhélie de cette planète". Comptes rendus hebdomadaires des séances de l'Académie des Sciences. 49: 379–383.
- ↑ Worrall, Simon (4 November 2015). "The Hunt for Vulcan, the Planet That Wasn't There". National Geographic.
- ↑ Levine, Alaina G. (May 2016). "May 29, 1919: Eddington Observes Solar Eclipse to Test General Relativity". This Month in Physics History. APS News. American Physical Society.
- ↑ Hobson, M. P.; Efstathiou, G.; Lasenby, A. N. (2006). General Relativity. Cambridge: Cambridge University Press. pp. 176–179.
- ↑ Thorne, Kip S. (1988). Fairbank, J. D.; Deaver Jr., B. S.; Everitt, W. F.; Michelson, P. F. (eds.). Near zero: New Frontiers of Physics (PDF). W. H. Freeman and Company. pp. 573–586.
- ↑ Feynman, R. P.; Leighton, R. B.; Sands, M. (1964). The Feynman Lectures on Physics, vol. 2 (New Millenium ed.). Basic Books. pp. 13–6 to 13–11.
- ↑ Williams, R. K. (1995). "Extracting X rays, Ύ rays, and relativistic e−–e+ pairs from supermassive Kerr black holes using the Penrose mechanism". Physical Review D. 51 (10): 5387–5427. Bibcode:1995PhRvD..51.5387W.
- ↑ Williams, R. K. (2004). "Collimated escaping vortical polar e−–e+ jets intrinsically produced by rotating black holes and Penrose processes". The Astrophysical Journal. 611 (2): 952–963. arXiv:astro-ph/0404135.
- ↑ Kuroda, Takami; Kotake, Kei; Takiwaki, Tomoya (2012). "Fully General Relativistic Simulations of Core-Collapse Supernovae with An Approximate Neutrino Transport". The Astrophysical Journal. 755 (1): 11. arXiv:1202.2487.
- ↑ Wollack, Edward J. (10 December 2010). "Cosmology: The Study of the Universe". Universe 101: Big Bang Theory. NASA.
- ↑ 가 나 Bondi, Hermann (1957). DeWitt, Cecile M.; Rickles, Dean (eds.). The Role of Gravitation in Physics: Report from the 1957 Chapel Hill Conference. Berlin: Max Planck Research Library. pp. 159–162.
- ↑ Crowell, Benjamin (2000). General Relativity. Fullerton, CA: Light and Matter. pp. 241–258.
- ↑ Kreuzer, L. B. (1968). "Experimental measurement of the equivalence of active and passive gravitational mass". Physical Review. 169 (5): 1007–1011. Bibcode:1968PhRv..169.1007K.
- ↑ Will, C. M. (1976). "Active mass in relativistic gravity-Theoretical interpretation of the Kreuzer experiment". The Astrophysical Journal. 204: 224–234.
- ↑ Bartlett, D. F.; Van Buren, Dave (1986). "Equivalence of active and passive gravitational mass using the moon". Phys. Rev. Lett. 57 (1): 21–24. Bibcode:1986PhRvL..57...21B.
- ↑ "Gravity Probe B: FAQ". Retrieved 2 July 2017.
- ↑ Gugliotta, G. (16 February 2009). "Perseverance Is Paying Off for a Test of Relativity in Space". New York Times.
- ↑ Everitt, C.W.F.; Parkinson, B.W. (2009). "Gravity Probe B Science Results—NASA Final Report" (PDF).
- ↑ Everitt; et al. (2011). "Gravity Probe B: Final Results of a Space Experiment to Test General Relativity". Physical Review Letters. 106 (22): 221101. arXiv:1105.3456.
- ↑ Iorio, L. (February 2017). "A comment on "A test of general relativity using the LARES and LAGEOS satellites and a GRACE Earth gravity model. Measurement of Earth's dragging of inertial frames," by I. Ciufolini et al". The European Physical Journal C. 77 (2): 73. arXiv:1701.06474.
- ↑ Ciufolini, Ignazio; Paolozzi, Antonio Rolf Koenig; Pavlis, Erricos C.; Koenig, Rolf (2016). "A test of general relativity using the LARES and LAGEOS satellites and a GRACE Earth gravity model". Eur Phys J C. 76 (3): 120.
- ↑ Cartlidge, Edwin (20 January 2016). "Underground ring lasers will put general relativity to the test". physicsworld.com. Institute of Physics.
- ↑ "Einstein right using the most sensitive Earth rotation sensors ever made". Phys.org. Science X network.
- ↑ Murzi, Mauro. "Jules Henri Poincaré (1854–1912)". Internet Encyclopedia of Philosophy (ISSN 2161-0002). Retrieved 9 April 2018.
- ↑ Deser, S. (1970). "Self-Interaction and Gauge Invariance". General Relativity and Gravitation. 1 (18): 9–8. arXiv:gr-qc/0411023.
- ↑ Grishchuk, L. P.; Petrov, A. N.; Popova, A. D. (1984). "Exact Theory of the (Einstein) Gravitational Field in an Arbitrary Background Space–Time". Communications in Mathematical Physics. 94 (3): 379–396.
- ↑ Rosen, N. (1940). "General Relativity and Flat Space I". Physical Review. 57 (2): 147–150. Bibcode:1940PhRv...57..147R.
- ↑ Weinberg, S. (1964). "Derivation of Gauge Invariance and the Equivalence Principle from Lorentz Invariance of the S-Matrix". Physics Letters. 9 (4): 357–359. Bibcode:1964PhL.....9..357W.
- ↑ 가 나 Thorne, Kip (1995). Black Holes & Time Warps: Einstein's Outrageous Legacy. W. W. Norton & Company.
- ↑ Bondi, H.; Van der Burg, M.G.J.; Metzner, A. (1962). "Gravitational waves in general relativity: VII. Waves from axisymmetric isolated systems". Proceedings of the Royal Society of London A. A269 (1336): 21–52. Bibcode:1962RSPSA.269...21B.
- ↑ Sachs, R. (1962). "Asymptotic symmetries in gravitational theory". Physical Review. 128 (6): 2851–2864. Bibcode:1962PhRv..128.2851S.
- ↑ Strominger, Andrew (2017). "Lectures on the Infrared Structure of Gravity and Gauge Theory". arXiv:1703.05448. ...redacted transcript of a course given by the author at Harvard in spring semester 2016. It contains a pedagogical overview of recent developments connecting the subjects of soft theorems, the memory effect and asymptotic symmetries in four-dimensional QED, nonabelian gauge theory and gravity with applications to black holes. To be published Princeton University Press, 158 pages."
- ↑ maths.tcd.ie
- ↑ 가 나 다 라 Bär, Christian; Fredenhagen, Klaus (2009). "Lorentzian Manifolds" (PDF). Quantum Field Theory on Curved Spacetimes: Concepts and Mathematical Foundations. Dordrecht: Springer. pp. 39–58.
- ↑ Tegmark, Max (1 April 1997). "On the dimensionality of spacetime". Classical and Quantum Gravity. 14 (4): L69–L75. arXiv:gr-qc/9702052.
- ↑ Skow, Bradford (2007). "What makes time different from space?" (PDF). Noûs. 41 (2): 227–252.
- ↑ Leibniz, Gottfried (1880). "Discourse on Metaphysics". Die philosophischen schriften von Gottfried Wilhelm Leibniz, Volume 4. Weidmann. pp. 427–463.
- ↑ Ehrenfest, Paul (1920). "How do the fundamental laws of physics make manifest that Space has 3 dimensions?". Annalen der Physik. 61 (5): 440–446. Also see Ehrenfest, P. (1917) "In what way does it become manifest in the fundamental laws of physics that space has three dimensions?" Proceedings of the Amsterdam Academy20: 200.
- ↑ Weyl, H. (1922). Space, time, and matter. Dover reprint: 284.
- ↑ Tangherlini, F. R. (1963). "Atoms in Higher Dimensions". Nuovo Cimento. 14 (27): 636. doi:10.1007/BF02784569.
- ↑ 가 나 다 Tegmark, Max (April 1997). "On the dimensionality of spacetime" (PDF). Classical and Quantum Gravity. 14 (4): L69–L75.
- ↑ Feng, W.-X. (3 August 2022). "Gravothermal phase transition, black holes and space dimensionality". Physical Review D. 106 (4): L041501. arXiv:2207.14317
- ↑ Scargill, J. H. C. (26 February 2020). "Existence of life in 2 + 1 dimensions". Physical Review Research. 2 (1): 013217.
- ↑ "Life could exist in a 2D universe (according to physics, anyway)". MIT Technology Review. Retrieved 16 June 2021.
추가 자료[편집]
- Barrow, John D.; Tipler, Frank J. (1986). The Anthropic Cosmological Principle (1st ed.). Oxford University Press.
- George F. Ellis and Ruth M. Williams (1992) Flat and curved space–times. Oxford Univ. Press.
- Lorentz, H. A., Einstein, Albert, Minkowski, Hermann, and Weyl, Hermann (1952) The Principle of Relativity: A Collection of Original Memoirs. Dover.
- Lucas, John Randolph (1973) A Treatise on Time and Space. London: Methuen.
- Penrose, Roger (2004). The Road to Reality. Oxford: Oxford University Press. Chpts. 17–18.; 로저 펜로즈 《실체에 이르는 길 1, 2》 박병철 옮김. 승산, 2010.
- Taylor, E. F.; Wheeler, John A. (1992). Spacetime Physics, Second Edition. Internet Archive: W. H. Freeman.
- Arkani-Hamed, Nima (1 December 2017). The Doom of Spacetime: Why It Must Dissolve Into More Fundamental Structures (Speech). The 2,384Th Meeting Of The Society. Washington, D.C. Retrieved 16 July 2022.
외부 링크[편집]
 위키미디어 공용에 시공간 관련 미디어 분류가 있습니다.
위키미디어 공용에 시공간 관련 미디어 분류가 있습니다.- Albert Einstein on space–time 13th edition Encyclopædia Britannica Historical: Albert Einstein's 1926 article
- Encyclopedia of Space–time and gravitation Scholarpedia Expert articles
- Stanford Encyclopedia of Philosophy: "Space and Time: Inertial Frames" by Robert DiSalle.







































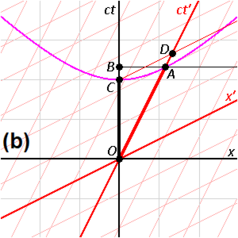



























































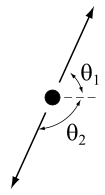





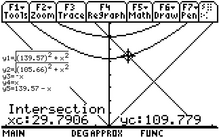


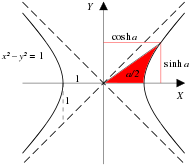


































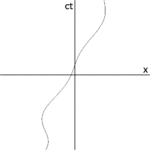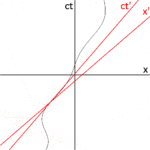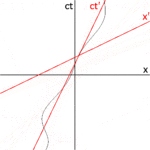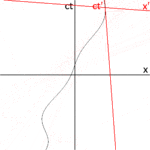







































![{\displaystyle -\,\left(1+{\frac {2GM}{c^{2}r}}\right)\left[(\Delta x)^{2}+(\Delta y)^{2}+(\Delta z)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e004b8eb220d5cc0f0e835a4f9a584ebfdc3ef02)
![{\displaystyle \left[(\Delta x)^{2}+(\Delta y)^{2}+(\Delta z)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b88b386b994cad15b04251eedd908b3828db4d66)



























