중력 특이점

슈바르츠실트 블랙홀이 가시선 평면에서 배경 은하로 통과하면서 발생하는 중력 렌즈의 애니메이션 시뮬레이션. 정확한 정렬(합충) 부근과 그 시점에 빛의 극단적 렌즈 효과가 관찰된다.

한 중력 특이점(gravitational singularity), 시공간 특이점 또는 간단하게 특이점은 중력이 아주 강해서 시공간 자체가 파국적으로 붕괴될 것으로 예측되는 어떤 상태를 말한다. 따라서 그러한 한 특이점은 정의상 더 이상 일반적 시공간에 속하지 않으며 또한 "어디"나 "언제"로 결정할 수 없다. 중력 특이점은 일반 상대성이론과 양자역학의 교차점에 존재하므로, 양자 중력 이론이 확립되지 않으면 특이점의 특성이 설명될 수 없다. 현재 최고의 중력 이론인 일반 상대성이론에서 특이점에 대한 완전하고 정확한 정의를 찾는 것은 한 어려운 문제로 남아 있다. 일반 상대성이론에서 한 특이점은 스칼라 불변량(scalar invariant) 곡률이 무한대가 되거나, 더 좋게는, 한 측지선이 불완전한 것으로 정의될 수 있다.

중력 특이점들은 주로 일반 상대성이론의 맥락에서 고려되는데, 여기서 양자역학으로부터의 보정 없이는 어떤 블랙홀 중심에서, 그리고 천체물리학 및 우주론 내에서 대폭발(빅뱅) 당시 [[w:Initial singulari우주의 최초 상태{Initial singularity}]]에서 밀도는 무한대가 될 것이다. 물리학자들은 특이점들의 예측이 특이점이 실제로 존재한다는 의미인지(또는 대폭발이 시작될 때 존재했다는 것인지), 또는 현재의 지식이 그러한 극한 밀도들에서 일어나는 것을 설명하기에 불충분하다는 의미인지 결정하지 못한다.

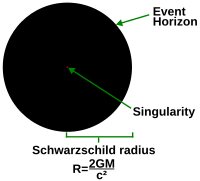
일반 상대성이론은 특정 지점(별들의 경우는 이것은 슈바르츠실트 반지름이 될 것이다)을 넘어 붕괴하는 모든 물체는 블랙홀을 형성하고, 그 내부에 한 특이점(어떤 사건 지평선으로 덮인)이 형성될 것이라고 예측한다. 펜로즈-호킹 특이점 정리는 한 특이점을 한 매끄러운 방식으로 확장할 수 없는 측지선을 갖는 것으로 정의한다. 이러한 측지선의 종점이 특이점으로 간주된다.

현대 이론은, 대폭발이 시작될 때, 우주의 최초 상태가 한 특이점이라고 주장한다. 이 경우 우주는 블랙홀로 붕괴되지 않았는데, 이는 현재 알려진 중력 붕괴에 대한 계산과 밀도 한계가 일반적으로 별들과 같이 상대적으로 일정한 크기의 물체를 기반으로 하며, 또한 대폭발과 같이 급격하게 팽창하는 공간에는 반드시 같은 방식으로 적용되지 않기 때문이다. 일반 상대성이론이나 양자역학 모두 현재 대폭발(빅뱅)의 최초 순간들을 설명할 수 없지만, 일반적으로는, 양자역학은 입자들이 그 파장들 보다 한 작은 공간에 서식하는 것을 허용하지 않는다.

해석

물리학의 많은 이론들에는 어떤 종류의 수학적 특이점들이 있다. 이러한 물리 이론들의 방정식들은 어떤 양의 질량의 공이 무한대가 되거나 또는 무한대로 증가한다고 예측한다. 이것은 일반적으로 라모 공식에 의해 예측되는 어떤 수소 원자의 자외선 파탄, 재규격화 및 불안정성에서와 같이 그 이론에서 한 누락된 부분이 있다는 신호이다.

일반 상대성이론이 아닌 특수 상대성이론을 포함하는 고전장 이론에서는, 시공간에서 특정 물리적 특성이 정의되지 않는 특정 지점에서 한 해가 한 특이점을 가지며, 시공간은 그 특이점을 위치시키기 위한 배경 장 역할을 한다고 말할 수 있다. 반면에 일반 상대성이론에서 한 특이점은 시공간 자체가 잘못 정의되고, 특이점이 더 이상 일반적 시공간 다양체의 일부가 아니기 때문에 더욱 복잡하다. 일반 상대성이론에서, 한 특이점은 "어디서" 또는 "언제"로 정의될 수 없다.

루프 양자중력 이론과 같은 일부 이론들은 특이점이 존재하지 않을 수 있다고 제안한다. 이것은 아인슈타인-맥스웰-디랙 방정식과 같은 고전적인 통일장 이론에서도 마찬가지이다. 그 아이디어는 양자 중력 효과로 인해 질량들 사이의 거리가 짧아짐에 따라 중력이 더 이상 계속 증가하지 않는 최소 거리가 존재한다거나, 또는 대안적으로 서로 관통하는 입자 파동들이 먼 거리에서 느낄 수 있는 중력 효과들을 가린다는 형식으로 언급될 수 있다.

이러한 루프 양자중력의 철학에서 영감을 받아 최근에는 이러한 개념이 기하학의 첫 번째 공리, 즉, 한 점을 나타내거나 증명하는 작은 점의 연장을 설명하는, 산술과 기하학의 융합이라고 부르는 한 프로그램적 호출에 기반한 클라인의 처방을 고려함으로써, 점의 개념을 정교화한 몇 가지 기본 구성을 통해서 실현될 수 있음이 밝혀졌다. 보른에 따르면, 클라인의 프로그램은 실제로 '실수'들을 사용하여 '한 물리적 상황'을 설명하면서 '모든 관측의 자연적 불확실성'을 고려하는 한 수학적 경로였다.

유형

원뿔형과 곡선형 등 특이점이 처음 등장한 이론들과 관련된 특성들을 가진 물리적 특징이 각각 다른 한 가지 유형의 특이점만이 존재한다. 또한 사건 지평선들 없이 발생한다는 가설도 있는데, 사건 지평선 너머에는 사건들이 영향을 미칠 수 없는 한 시공간 구간을 다른 시공간 구간과 구분하는 구조이다; 이것들은 벌거숭이라고 불린다.

원뿔형

한 원뿔형 특이점은 일부 미분동형사상 공변(diffeomorphism covariance)량의 한계가 존재하지 않거나 무한한 지점이 있을 때 발생하며, 이 경우 한계점 자체에서 시공간이 매끄럽지 않다. 따라서, 시공간은 이 지점을 중심으로 원뿔처럼 보이며, 그 특이점은 원뿔의 끝에 위치한다. 좌표계가 사용되는 모든 곳에서 그 계량은 유한할 수 있다.

이러한 원뿔형 특이점의 한 예는 우주 끈 그리고 슈바르츠실트 블랙홀이다.

곡률

회전하지 않는 블랙홀과 그 특이점에 대한 간단한 도해

일반 상대성이론이나 다른 중력 이론(초중력와 같은)의 방정식들을 풀다 보면 계량(metric)이 무한대로 불어나는 지점을 만나게 되는 경우가 종종 있다. 그렇지만, 이러한 점들 대부분은 완전히 정칙적이고 또한 무한대들은 이 점에서 부적절한 좌표계를 사용한 어떤 결과(using an inappropriate coordinate system at this point}일 뿐이다. 한 특정 지점에 한 특이점이 있는지 테스트하려면 이 지점에서 미분동형사상 불변(diffeomorphism invariant)량들(즉, 스칼라들)이 무한대가 되는지 확인해야만 한다. 이러한 양들은 모든 좌표계에서 동일하므로 한 좌표들의 변화에 의해서 무한대가 "사라지지" 않는다.

어떤 회전하지 않고 대전되지 않은 블랙홀을 설명하는 슈바르츠실트 해가 한 예이다. 블랙홀로부터 멀리 떨어진 영역들에서 작업하기에 편리한 좌표계들에서는 사건의 지평선에서 계량의 일부가 무한대가 된다. 그렇지만, 사건의 지평선에서의 시공간은 정칭적이다. 그 계량이 완벽하게 매끄러운 다른 좌표계(예: 크루스칼 좌표(Kruskal coordinates))로 변경할 때, 그 정칙성은 분명해진다. 다른 한편으로는, 블랙홀의 중심에서 계량이 무한대가 되는 경우, 해법들은 한 특이점이 존재함을 시사한다. 특이점의 존재는 크레취만 스칼라(Kretschmann scalar)를 통해 확인할 수 있는데, 이것은 리만 텐서의 제곱 즉 $R_{\mu \nu \rho \sigma }R^{\mu \nu \rho \sigma }$이며, 이것은 미분동형사상 불변이고, 무한대이다.

어떤 회전하지 않는 블랙홀에서는 그 특이점이 모형 좌표들의 한 점에서 발생하는데, 이를 "점 특이점"이라고 불리며, 한편 커 블랙홀이라고도 하는 회전하는 블랙홀에서는 그 특이점이 "고리 특이점(ring singularity)"이라고도 알려진 한 고리(원형 선)에서 발생한다. 이러한 특이점은 이론적으로 한 웜홀이 될 수도 있다.

보다 일반적으로는, 만일 한 시공간이 측지적으로 불완전한(geodesically incomplete) 경우, 즉 그 특이점에 도달하는 시점 이후, 즉 유한한 시간을 넘어서는 운동을 결정할 수 없는 자유 낙하 입자들가 있음을 의미하며, 그것은 특이점으로 간주된다. 예를 들어, 회전하지 않는 블랙홀의 사건 지평선 안에 있는 모든 관측자는 유한한 시간 내에 그 중심에 떨어지게 된다. 고전적인 버전의 우주의 대폭발(빅뱅) 우주론적 모형은 시간의 시작 (t=0)에 한 인과적 특이점을 포함하며, 여기서 모든 시간꼴 측지선은 과거로 확장하지 않는다. 이 가상의 시간 0으로 뒤돌아 외삽하면 크기가 영인 모든 공간 차원들, 무한 밀도, 무한 온도 및 무한 시공간 곡률을 가진 우주가 된다.

벌거숭이 특이점

1990년대 초까지만 해도, 일반 상대성이론은 모든 특이점을 어떤 사건의 지평선 뒤에 숨겨서 벌거숭이 특이점들은 불가능하다고 널리 믿었다. 이를 우주 검열 가설이라고 한다. 그렇지만, 1991년 물리학자 스튜어트 샤피로_{Stuart Shapiro}와 사울 테우콜스키(Saul Teukolsky)_{Saul Teukolsky}는 먼지의 회전하는 평면에 대한 컴퓨터 시뮬레이션을 수행하여 일반 상대성이론이 "벌거숭이" 특이점들을 허용할 수 있음을 보여주었다. 이러한 모형에서 이러한 천체들이 실제로 어떻게 보일지는 알려지지 않았다. 또한 시뮬레이션에 사용된 단순화 가정을 제거해도 특이점들이 여전히 발생할지 여부도 알 수 없다. 그렇지만, 한 특이점에 들어오는 빛도 유사하게 그 측지선이 종료되고, 따라서 그 벌거숭이 특이점이 한 블랙홀처럼 보일 것이라는 가설이 있다.

한 진공에서 회전하는 블랙홀인 커 계량에서, 만일 각운동량($J$)이 충분히 높으면, 사라지는 사건 지평선들이 존재한다. 커 계량을 보이어-린드퀴스트 좌표(Boyer–Lindquist coordinates)로 변환하면, 사건 지평선의 좌표(반지름이 아님)는 $r_{\pm }=\mu \pm \left(\mu ^{2}-a^{2}\right)^{1/2}$, 여기서  $\mu =GM/c^{2}$ 그리고 $a=J/Mc$. 이 경우, "사건의 지평선이 사라진다"는 것은 해들이 $r_{\pm }$, 또는 $\mu ^{2}<a^{2}$를 위해 복소수일 때를 의미한다는 것이 보여질 수 있다. 그렇지만, 이것은 $J$가 $GM^{2}/c$ (또는 플랑크 단위로 $J>M^{2}$)를 초과한다; 즉 그 스핀이 일반적으로 물리적으로 가능한 값의 상한으로 간주되는 것을 초과하는 경우에 해당한다.

유사하게, 사라지는 사건의 지평선들은. 만일 전하($Q$)가 충분히 높은 경우에, 대전된 블랙홀의 라이스너-노르드스트룀 기하학적 구조에서도 또한 볼 수 있다. 이 계량에서, 특이점이 $\mu =GM/c^{2}$, 그리고 $q^{2}=GQ^{2}/\left(4\pi \epsilon _{0}c^{4}\right)$인 $r_{\pm }=\mu \pm \left(\mu ^{2}-q^{2}\right)^{1/2}$에서 발생한다는 것이 보여질 수 있다. $\mu$와 $q$의 상대적인 값들에 대해 가능한 세 가지 경우 중, $\mu ^{2}<q^{2}$는 $r_{\pm }$가 모두 복소수인 경우이다. 이는 계량이 $r$의 모든 양의 값에 대해 정칙적이거나, 다시 말해 특이점에는 사건의 지평선이 없다는 것을 의미한다. 그렇지만, 이는 $Q/{\sqrt {4\pi \epsilon _{0}}}$가 $M{\sqrt {G}}$(또는 플랑크 단위로는 $Q>M$), 즉 전하가 일반적으로 물리적으로 가능한 값의 상한으로 간주되는 것을 초과하는 경우에 해당한다. 또한, 실제 천체물리학적 블랙홀들은 어떤 상당한 전하를 갖지 않을 것으로 예측된다.

$J$ 및 $Q$ 값과 위에서 언급한 한계와 일치하는 가장 낮은 $M$ 값을 갖는 어떤 블랙홀, 즉 사건의 지평선을 잃기 직전의 것은 임계 블랙홀이라고 용어화 된다.

엔트로피

 블랙홀, 호킹 복사 및 엔트로피 문서를 참고하십시오.

스티븐 호킹이 호킹 복사 개념을 생각해 내기 전에는, 블랙홀들이 엔트로피를 갖는다는 질문은 회피되어 왔다. 그렇지만, 이 개념은 블랙홀들이 에너지를 방출하여 엔트로피를 보존하고 열역학 제2법칙과 비양립적인 문제를 해결한다는 것을 보여준다. 엔트로피는 하지만 열을 의미하고 또한 온도를 의미한다. 그 에너지 손실은 또한 블랙홀이 영원히 지속되는 것이 아니라 증발하거나 천천히 붕괴한다는 것을 의미한다. 블랙홀 온도는 질량에 반비례한다. 모든 알려진 블랙홀 후보들은 너무 커서 그 온도가 우주 배경 복사 것보다 훨씬 낮은데, 이것은 그것들이 이 복사를 흡수하여 순 에너지를 얻게 되는 것을 의미한다. 그들은 배경 온도가 자신의 온도 아래로 떨어질 때까지 순 에너지를 잃기 시작할 수 없다. 이것은 배경 복사가 형성된 이후 천 개 정도가 아니라 백만 개 이상의 우주 적색편이 중 하나에서 발생할 것이다.

같이 보기

• 0-차원 특이점: 자기 홀극
• 1-차원 특이점: 우주 끈
• 2-차원 특이점: 도메인 벽(domain wall)
• 퍼즈볼
• 펜로즈–호킹 특이점 정리
• 화이트홀
• BKL 특이점(BKL singularity)
• 최초 특이점(initial singularity)

참고 문헌

• Earman, John (1995). 《Bangs, crunches, whimpers, and shrieks: Singularities and acausalities in relativistic spacetimes》. Oxford University Press. ISBN 019509591X. 
• Joshi, Pankaj S (2007). 《Gravitational collapse and spacetime singularities》. New York: Cambridge University Press. ISBN 9781107405363. 
• Misner, Charles W.; Thorne, Kip; Wheeler, John Archibald (1973). 《Gravitation》. W. H. Freeman. ISBN 0-7167-0344-0.  §31.2 The nonsingularity of the gravitational radius, and following sections; §34 Global Techniques, Horizons, and Singularity Theorems
• Wald, Robert M. (1984). 《General Relativity》. University of Chicago Press. ISBN 0-226-87033-2. 

• Hawking, S. W.; Penrose, R. (1970), “The Singularities of Gravitational Collapse and Cosmology”, 《Proc. R. Soc. A》 314 (1519): 529–548, Bibcode:1970RSPSA.314..529H, doi:10.1098/rspa.1970.0021  (Free access.)
• Shapiro, Stuart L.; Teukolsky, Saul A. (1991). “Formation of naked singularities: The violation of cosmic censorship” (PDF). 《Physical Review Letters》 66 (8): 994–997. Bibcode:1991PhRvL..66..994S. doi:10.1103/PhysRevLett.66.994. PMID 10043968. S2CID 7830407. 
• Penrose, Roger (1996). "Chandrasekhar, Black Holes, and Singularities". ias.ac.in.
• Penrose, Roger (1999). "The Question of Cosmic Censorship". ias.ac.in.
• Singh, T.P. (1999) "Gravitational Collapse, Black Holes and Naked Singularities". ias.ac.in.

추가 읽기

• 《엘러건트 유니버스》 브라이언 그린 지음. 이 책은 비전문가를 위한 끈 이론 입문서이지만, 일부 내용은 이미 구식이 되어가고 있다. 일반적인 용어를 사용하고 본문 전반에 걸쳐 예제들을 제공함으로써 비전문가가 끈 이론의 기초를 이해하는 데 도움이 된다.