열역학 제2법칙
| 열역학 법칙 |
|---|
| 열역학 제0법칙 |
| 열역학 제1법칙 |
| 열역학 제2법칙 |
| 열역학 제3법칙 |
| 상반 법칙
|
물리학에서 열역학 제2법칙(second law of thermodynamics)은 열적으로 고립된 계에서 매 시각마다 계의 거시상태의 엔트로피를 고려하였을 때, 엔트로피가 더 작은 거시상태로는 진행하지 않는다는 법칙이다. 즉, "열은 항상 뜨거운 곳에서 차가운 곳으로 흐른다"와 같으며, "열역학 사이클에서 모든 열이 일로 변환될 수는 없다"와도 같다.[1][2][3]
이 법칙을 통해 자연적인 과정의 비가역성과 미래와 과거 사이의 비대칭성을 설명한다. 하지만 엔트로피가 감소된 거시상태가 될 확률은 극히 낮을 뿐 불가능은 아니다.
열역학 제2법칙은 열역학계의 물리적 성질로서 엔트로피의 개념을 정립한다. 열역학 제1법칙에 나타난 에너지 보존의 요구를 따르더라도 금지되는 열적 과정이 있으며, 어떤 과정이 자발적으로 일어나기 위해 필요한 기준을 제시한다. 예를 들어 제1법칙은 컵이 탁자에서 떨어져 깨지는 것과 컵 조각들이 다시 모여 테이블로 뛰어드는 두 과정을 모두 허용하는 반면, 제2법칙은 전자를 허용하고 후자를 부정한다. 자연 과정의 비가역성은 시간의 화살이라는 용어로 설명되기도 한다.[4][5]
제2법칙은 경험적 발견이며, 역사적으로 열역학 이론의 공리로 받아들여지게 되었다. 통계역학은 원자 또는 분자의 큰 집합체 상태들의 확률 분포의 관점에서 법칙을 미시적으로 설명한다. 제2법칙은 여러 공식으로 표현된다. 엔트로피의 적절한 정의에 선행하고 열소이론(caloric theory)에 기초한 첫 번째 정의는 카르노 기관과 함께 제안된 카르노 정리로, 1824년 열기관에서 일을 하는 열의 변환 효율이 상한을 갖는다는 것을 보여준 프랑스 과학자 사디 카르노가 제안한 것이다.[6][7] 엔트로피의 개념에 기초한 제2법칙의 엄격한 첫 번째 정의는 1850년대 독일 과학자 루돌프 클라우지우스가 제안한 것으로, 열은 동시에 일어나는 또다른 변화 없이는 더 차가운 물체에서 더 따뜻한 물체로 절대 전달될 수 없다는 해설을 덧붙였다.
열역학 제2법칙은 열역학적 온도 개념을 정의할 수 있게 하지만, 현재는 공식적으로 열역학 제0법칙이 그 정의를 하는 것으로 이해한다.
내용[편집]
열역학 2법칙을 통해 차가운 부분에 한 일이 없을 때, 열이 차가운 부분에서 뜨거운 부분으로 흐르지 않는 이유와 열원(reservoir)에서 열에너지가 모두 일로 전환될 때, 다른 추가적인 효과를 동반하지 않는 순환과정(cycle)은 존재하지 않는다는 점에 대해 설명할 수 있다.
열역학 제2법칙의 모순처럼, 고립계가 아닌 계의 엔트로피는 감소하는 것으로 볼 수도 있다. 예를 들어 에어컨은 방 안의 공기를 차갑게 해주어서 공기의 엔트로피를 감소시킨다. 하지만 방 안으로부터 방출되거나 에어컨이 작동함에 따라 흡수되는 열은 항상 그 계의 공기의 엔트로피의 감소보다 많은 양의 엔트로피를 생성한다. 따라서 전체 계의 총 엔트로피는 열역학 제2법칙에 의하듯 증가한다.
역학에서 열역학의 기본 관계를 사용하여 표현된 제2법칙은 계의 일을 할 수 있는 능력의 한계를 나타낸다. 가역과정에서 미소 열 을 흡수한 온도가 T인 계의 엔트로피 변화는 로 주어진다.
열역학 제1법칙이 과정 전, 그리고 후의 에너지를 양적(量的)으로 규제하는 반면, 열역학 제2법칙은 에너지가 흐르는 방향을 규제한다.[8]
다른 표현[편집]
열역학 제2법칙은 다양한 방법으로 서술될 수 있다.[9] 카르노가 처음으로 시도하였으며, 이후 학문적으로 엄격한 정의는 루돌프 클라우지우스(1854), 켈빈 남작(1851), 콘스탄티노스 카라테오도리(1909)의 서술이 대표적이다.[10] 이러한 서술은 특정한 과정의 불가능성을 언급하면서 일반적인 물리적 용어들을 제시했다. 클라우지우스의 서술과 켈빈의 서술은 동등한 것으로 여겨진다.[11]
카르노 정리[편집]
니콜라 레오나르 사디 카르노는 1824년 열기관에서 일을 하는 열의 변환 효율이 상한을 갖는다는 것을 보였는데, 열역학 제2법칙에 대한 역사적으로 최초의 기록이다.[12] 카르노는 분석결과 이상적인 열기관은 매 순간 열평형상태에 놓여 준정적(準静的, Quasi-static) 과정을 할 때 가능하다고 결론지었는데, 이 이상적 열기관을 카르노 기관이라 한다.
클라우지우스의 정의[편집]
1854년, 독일의 물리학자 루돌프 클라우지우스는 저온의 물체에서 고온의 물체로 열을 전달시키는 것이 유일한 결과인 과정은 불가능하다고 서술했다.[9] 즉, 엔트로피는 고립계에서 항상 증가한다는 것이다.[13]
켈빈-플랑크의 정의[편집]
켈빈 남작과 막스 플랑크는 열원으로부터 열을 전부 흡수하여 일로 바꾸는 과정은 불가능하며 열을 일로 전환하기 위해서는 반드시 열이 높은 곳에서 낮은 곳으로 이동해야 한다고 했다.[9]
클라우지우스와 켈빈-플랑크 정의의 동등성[편집]
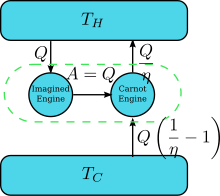
우측 그림에서 볼 수 있듯 같이 켈빈의 정의와 클라우지우스의 정의는 같은 것이다. 켈빈의 정의를 위반하는 기관이 있다고 해보자. 즉, 주위와 어떠한 상호작용 없이 흡수한 열을 전부 일로 변환하는 기관이 있다고 해보자. 이는 우측 그림에서 볼 수 있듯 카르노 기관(Carnot engine)의 역과정이다. 이 기관의 효율은 최대 효율인 η인데, 결론적으로 저온에서 고온으로 만큼의 열을 전달하는 기관이 되어 클라우지우스의 정의를 위반하게 된다. 따라서 둘 중 하나를 위배하는 경우 다른 하나를 자동적으로 위반하게 된다.
통계 역학[편집]
엔트로피가 확률에 의해 지배받는 요소라는 것을 입증한다. 따라서 무질서의 감소가 닫힌계 안에서도 일어날 수 있다. 그러나 이것이 나타날 확률은 매우 작기 때문에 이러한 현상이 나타나더라도 계의 매우 적은 입자들에만 영향을 미치는 일시적인 감소이다.
영구기관[편집]
열역학 제 2법칙은 영구기관의 불가능성을 정리하는 데 큰 기여를 했다. 열역학 제1법칙이 과정 전과 후의 에너지를 양적(量的)으로 규제하고 있는 데 비하여, 제2법칙은 에너지가 흐르는 방향을 규제하는 성격을 띠고 있다. 즉 에너지의 흐름은 엔트로피가 증가하는 방향으로 흐른다는 것이다. 따라서 이 법칙에 따르면, 하나의 열원에서 열을 받아 이것을 일로 바꾸되 그외 어떤 외부의 변화도 일으키지 않는 열기관인 제2종 영구기관의 제작은 불가능하다고 할 수 있다. 제2종 영구기관은 100%열을 받아서 100%운동에너지로 바꿀 수 있는 기관이다. 그렇지만 켈빈-플랑크의 기술에 의하면 제2종 영구기관의 제작은 불가능하다고 했다. 효율이 좋은 기관의 제작은 가능하지만 영구기관을 만드는 것은 불가능하다.[8]
같이 보기[편집]
각주[편집]
- ↑ Reichl, Linda (1980). 《A Modern Course in Statistical Physics》. Edward Arnold. 9쪽. ISBN 0-7131-2789-9.
- ↑ Rao, Y. V. C. (1997). 《Chemical Engineering Thermodynamics》. Universities Press. 158쪽. ISBN 978-81-7371-048-3.
- ↑ Young, H. D; Freedman, R. A. (2004). University Physics, 11th edition. Pearson. p. 764.
- ↑ {David Sanborn Scott, The arrow of time, International Journal of Hydrogen Energy, Volume 28, Issue 2, 2003, Pages 147-149, ISSN 0360-3199}
- ↑ Carroll, Sean (2010). 《From Eternity to Here: The Quest for the Ultimate Theory of Time》. Dutton. ISBN 978-0-525-95133-9.
- ↑ Jaffe, R.L.; Taylor, W. (2018). 《The Physics of Energy》. Cambridge UK: Cambridge University Press. 150, n259, 772, 743쪽. ISBN 978-1-107-01665-1.
- ↑ David L. Chandler (2011년 5월 19일). “Explained: The Carnot Limit”.
- ↑ 가 나 “[네이버 지식백과] 열역학 제2법칙 [the second law of thermodynamics, 熱力學第二法則] (두산백과)”.
- ↑ 가 나 다 “Concept and Statements of the Second Law”. web.mit.edu. 2010년 10월 7일에 확인함.
- ↑ Lieb & Yngvason (1999).
- ↑ Rao (2004), 213쪽.
- ↑ Carnot, S. (1824/1986).
- ↑ (Claus), Borgnakke, C. (2014). 《Fundamentals of thermodynamics》 8판. [Place of publication not identified]: John Wiley & Sons Inc. ISBN 1118321774.




