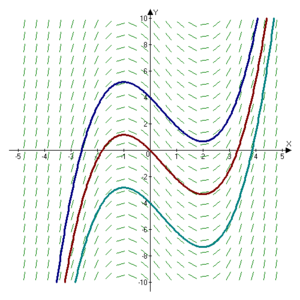
y
′
=
x
2
−
x
−
1
{\displaystyle y'=x^{2}-x-1}
기울기장 에 그려진 함수
f
(
x
)
=
x
2
−
x
−
1
{\displaystyle f(x)=x^{2}-x-1}
F
(
x
)
=
x
3
3
−
x
2
2
−
x
+
C
{\displaystyle \textstyle F(x)={\frac {x^{3}}{3}}-{\frac {x^{2}}{2}}-x+C}
C
=
−
4
,
0
,
4
{\displaystyle C=-4,0,4}
미적분학 에서 부정적분 (不定積分, 영어 : indefinite integral )은 어떤 함수 를 도함수 로 하는 모든 함수를 구하는 연산이다. 부정적분이 존재할 경우, 이는 항상 고정된 함수와 임의의 상수의 합의 꼴로 나타낼 수 있다. 따라서 상수만큼의 차를 무시하면 부정적분은 미분 또는 도함수 를 구하는 연산의 역연산이다.
함수
f
(
x
)
{\displaystyle f(x)}
x
∈
I
{\displaystyle x\in I}
F
(
x
)
{\displaystyle F(x)}
x
∈
I
{\displaystyle x\in I}
f
(
x
)
{\displaystyle f(x)}
원함수 (原函數, 영어 : antiderivative ) 또는 역도함수 (逆導函數)라고 한다.
F
′
(
x
)
=
f
(
x
)
∀
x
∈
I
{\displaystyle F'(x)=f(x)\qquad \forall x\in I}
함수
f
(
x
)
{\displaystyle f(x)}
x
∈
I
{\displaystyle x\in I}
F
(
x
)
{\displaystyle F(x)}
f
(
x
)
{\displaystyle f(x)}
∫
f
(
x
)
d
x
=
F
(
x
)
+
C
{\displaystyle \int f(x)\mathrm {d} x=F(x)+C}
이를
f
(
x
)
{\displaystyle f(x)}
부정적분 이라고 한다. 여기서
C
{\displaystyle C}
적분상수
C
{\displaystyle C}
(
C
)
′
=
0
{\displaystyle (C)'=0}
(
F
(
x
)
+
C
)
′
=
f
(
x
)
{\displaystyle (F(x)+C)'=f(x)}
F
(
x
)
+
C
{\displaystyle F(x)+C}
f
(
x
)
{\displaystyle f(x)}
G
(
x
)
{\displaystyle G(x)}
(
G
(
x
)
−
F
(
x
)
)
′
=
0
{\displaystyle (G(x)-F(x))'=0}
평균값 정리 에 따라
G
(
x
)
−
F
(
x
)
{\displaystyle G(x)-F(x)}
G
(
x
)
{\displaystyle G(x)}
G
(
x
)
=
F
(
x
)
+
C
{\displaystyle G(x)=F(x)+C}
위와 같은 꼴의 부정적분 공식은 정의역을 이루는 각각의 구간에서만 유효하다. 예를 들어,
f
(
x
)
=
1
/
x
2
{\displaystyle f(x)=1/x^{2}}
(
0
,
∞
)
{\displaystyle (0,\infty )}
(
−
∞
,
0
)
{\displaystyle (-\infty ,0)}
[ 1] :398-399
∫
1
x
2
d
x
=
−
1
x
+
C
{\displaystyle \int {\frac {1}{x^{2}}}\mathrm {d} x=-{\frac {1}{x}}+C}
전체 정의역
(
−
∞
,
0
)
∪
(
0
,
∞
)
{\displaystyle (-\infty ,0)\cup (0,\infty )}
[ 1] :398-399
∫
1
x
2
d
x
=
{
−
1
x
+
C
x
>
0
−
1
x
+
C
′
x
<
0
{\displaystyle \int {\frac {1}{x^{2}}}\mathrm {d} x={\begin{cases}\displaystyle -{\frac {1}{x}}+C&x>0\\\displaystyle -{\frac {1}{x}}+C'&x<0\end{cases}}}
만약
f
(
x
)
{\displaystyle f(x)}
(
∫
f
(
x
)
d
x
)
′
=
f
(
x
)
{\displaystyle \left(\int f(x)\mathrm {d} x\right)'=f(x)}
만약
F
(
x
)
{\displaystyle F(x)}
미분 가능 함수 라면 다음이 성립한다.
∫
F
′
(
x
)
d
x
=
F
(
x
)
+
C
{\displaystyle \int F'(x)\mathrm {d} x=F(x)+C}
이에 따라 상수 차를 무시하면 부정적분은 미분의 역연산이다.
연속 함수
f
(
x
)
{\displaystyle f(x)}
F
(
x
)
=
∫
a
x
f
(
x
)
d
x
{\displaystyle F(x)=\int _{a}^{x}f(x)\mathrm {d} x}
반대로, 연속 함수
f
(
x
)
{\displaystyle f(x)}
F
(
x
)
{\displaystyle F(x)}
∫
a
b
f
(
x
)
d
x
=
F
(
b
)
−
F
(
a
)
{\displaystyle \int _{a}^{b}f(x)\mathrm {d} x=F(b)-F(a)}
함수
f
(
x
)
,
g
(
x
)
{\displaystyle f(x),g(x)}
f
(
x
)
±
g
(
x
)
{\displaystyle f(x)\pm g(x)}
∫
f
(
x
)
±
g
(
x
)
d
x
=
∫
f
(
x
)
d
x
±
∫
g
(
x
)
d
x
{\displaystyle \int f(x)\pm g(x)\mathrm {d} x=\int f(x)\mathrm {d} x\pm \int g(x)\mathrm {d} x}
함수
f
(
x
)
{\displaystyle f(x)}
c
{\displaystyle c}
c
f
(
x
)
{\displaystyle cf(x)}
c
≠
0
{\displaystyle c\neq 0}
∫
c
f
(
x
)
d
x
=
c
∫
f
(
x
)
d
x
{\displaystyle \int cf(x)\mathrm {d} x=c\int f(x)\mathrm {d} x}
이에 따라 부정적분은 선형 연산이다.
만약
f
(
x
)
{\displaystyle f(x)}
F
(
x
)
{\displaystyle F(x)}
g
(
t
)
{\displaystyle g(t)}
[ 2] :246, 정리6.2.1
∫
f
(
g
(
t
)
)
g
′
(
t
)
d
t
=
∫
f
(
x
)
d
x
=
F
(
g
(
t
)
)
+
C
{\displaystyle \int f(g(t))g'(t)\mathrm {d} t=\int f(x)\mathrm {d} x=F(g(t))+C}
만약
g
(
t
)
{\displaystyle g(t)}
g
′
(
t
)
≠
0
{\displaystyle g'(t)\neq 0}
f
(
g
(
t
)
)
g
′
(
t
)
{\displaystyle f(g(t))g'(t)}
H
(
t
)
{\displaystyle H(t)}
[ 2] :252, 정리6.2.2
∫
f
(
x
)
d
x
=
∫
f
(
g
(
t
)
)
g
′
(
t
)
d
t
=
H
(
g
−
1
(
x
)
)
+
C
{\displaystyle \int f(x)\mathrm {d} x=\int f(g(t))g'(t)\mathrm {d} t=H(g^{-1}(x))+C}
만약
f
(
x
)
,
g
(
x
)
{\displaystyle f(x),g(x)}
f
′
(
x
)
g
(
x
)
{\displaystyle f'(x)g(x)}
∫
f
(
x
)
g
′
(
x
)
d
x
=
f
(
x
)
g
(
x
)
−
∫
f
′
(
x
)
g
(
x
)
d
x
{\displaystyle \int f(x)g'(x)\mathrm {d} x=f(x)g(x)-\int f'(x)g(x)\mathrm {d} x}
모든 (실수 ) 유리 함수 는 다항식과 진분수식의 합으로 나타낼 수 있으며, 모든 진분수식은 부분 분수 분해 를 통해 다음과 같은 꼴의 분수식들의 합으로 나타낼 수 있다.
A
(
x
−
a
)
m
{\displaystyle {\frac {A}{(x-a)^{m}}}}
B
x
+
C
(
x
2
+
p
x
+
q
)
n
{\displaystyle {\frac {Bx+C}{(x^{2}+px+q)^{n}}}}
여기서
A
,
B
,
C
,
a
,
p
,
q
∈
R
{\displaystyle A,B,C,a,p,q\in \mathbb {R} }
m
,
n
∈
Z
+
{\displaystyle m,n\in \mathbb {Z} ^{+}}
p
2
−
4
q
<
0
{\displaystyle p^{2}-4q<0}
∫
A
x
−
a
d
x
=
A
ln
(
x
−
a
)
+
C
{\displaystyle \int {\frac {A}{x-a}}\mathrm {d} x=A\ln(x-a)+C}
∫
A
(
x
−
a
)
m
d
x
=
−
A
(
m
−
1
)
(
x
−
a
)
m
−
1
+
C
(
m
>
1
)
{\displaystyle \int {\frac {A}{(x-a)^{m}}}\mathrm {d} x=-{\frac {A}{(m-1)(x-a)^{m-1}}}+C\qquad (m>1)}
∫
B
x
+
C
x
2
+
p
x
+
q
d
x
=
B
2
ln
(
x
2
+
p
x
+
q
)
+
2
C
−
B
p
4
q
−
p
2
arctan
2
x
+
p
4
q
−
p
2
+
C
{\displaystyle \int {\frac {Bx+C}{x^{2}+px+q}}\mathrm {d} x={\frac {B}{2}}\ln(x^{2}+px+q)+{\frac {2C-Bp}{\sqrt {4q-p^{2}}}}\arctan {\frac {2x+p}{\sqrt {4q-p^{2}}}}+C}
∫
B
x
+
C
(
x
2
+
p
x
+
q
)
n
d
x
=
−
B
2
(
n
−
1
)
(
x
2
+
p
x
+
q
)
n
−
1
+
(
C
−
B
p
/
2
)
∫
1
(
x
2
+
p
x
+
q
)
n
d
x
(
n
>
1
)
{\displaystyle \int {\frac {Bx+C}{(x^{2}+px+q)^{n}}}\mathrm {d} x=-{\frac {B}{2(n-1)(x^{2}+px+q)^{n-1}}}+(C-Bp/2)\int {\frac {1}{(x^{2}+px+q)^{n}}}\mathrm {d} x\qquad (n>1)}
∫
1
(
x
2
+
p
x
+
q
)
n
d
x
=
1
2
(
n
−
1
)
(
q
−
p
2
/
4
)
(
x
+
p
/
2
(
x
2
+
p
x
+
q
)
n
−
1
+
(
2
n
−
3
)
∫
1
(
x
2
+
p
x
+
q
)
n
−
1
d
x
)
(
n
>
1
)
{\displaystyle \int {\frac {1}{(x^{2}+px+q)^{n}}}\mathrm {d} x={\frac {1}{2(n-1)(q-p^{2}/4)}}\left({\frac {x+p/2}{(x^{2}+px+q)^{n-1}}}+(2n-3)\int {\frac {1}{(x^{2}+px+q)^{n-1}}}\mathrm {d} x\right)\qquad (n>1)}
부분 분수 분해의 각 항이 초등 함수이므로, 모든 유리 함수의 부정적분은 초등 함수이다.
삼각 유리 함수는
R
(
sin
x
,
cos
x
)
{\displaystyle R(\sin x,\cos x)}
R
(
u
,
v
)
{\displaystyle R(u,v)}
tan
x
2
=
t
,
x
=
2
arctan
t
,
d
x
=
2
1
+
t
2
d
t
{\displaystyle \tan {\frac {x}{2}}=t,\;x=2\arctan t,\;\mathrm {d} x={\frac {2}{1+t^{2}}}\mathrm {d} t}
그러면 원래의 부정적분은 유리 함수의 부정적분으로 변한다.
∫
R
(
sin
x
,
cos
x
)
d
x
=
∫
R
(
2
t
1
+
t
2
,
1
−
t
2
1
+
t
2
)
2
1
+
t
2
d
t
{\displaystyle \int R(\sin x,\cos x)\mathrm {d} x=\int R\left({\frac {2t}{1+t^{2}}},{\frac {1-t^{2}}{1+t^{2}}}\right){\frac {2}{1+t^{2}}}\mathrm {d} t}
만약
R
(
−
u
,
v
)
=
−
R
(
u
,
v
)
{\displaystyle R(-u,v)=-R(u,v)}
R
(
u
,
v
)
=
u
R
1
(
u
2
,
v
)
{\displaystyle R(u,v)=uR_{1}(u^{2},v)}
∫
R
(
sin
x
,
cos
x
)
d
x
=
∫
sin
x
R
1
(
sin
2
x
,
cos
x
)
d
x
=
−
∫
R
1
(
1
−
t
2
,
t
)
d
t
(
cos
x
=
t
)
{\displaystyle \int R(\sin x,\cos x)\mathrm {d} x=\int \sin xR_{1}(\sin ^{2}x,\cos x)\mathrm {d} x=-\int R_{1}(1-t^{2},t)\mathrm {d} t\qquad (\cos x=t)}
마찬가지로, 만약
R
(
u
,
−
v
)
=
−
R
(
u
,
v
)
{\displaystyle R(u,-v)=-R(u,v)}
R
(
u
,
v
)
=
v
R
1
(
u
,
v
2
)
{\displaystyle R(u,v)=vR_{1}(u,v^{2})}
∫
R
(
sin
x
,
cos
x
)
d
x
=
∫
cos
x
R
1
(
sin
x
,
cos
2
x
)
d
x
=
∫
R
1
(
t
,
1
−
t
2
)
d
t
(
sin
x
=
t
)
{\displaystyle \int R(\sin x,\cos x)\mathrm {d} x=\int \cos xR_{1}(\sin x,\cos ^{2}x)\mathrm {d} x=\int R_{1}(t,1-t^{2})\mathrm {d} t\qquad (\sin x=t)}
만약
R
(
−
u
,
−
v
)
=
R
(
u
,
v
)
{\displaystyle R(-u,-v)=R(u,v)}
R
(
u
,
v
)
=
R
1
(
u
/
v
,
v
2
)
{\displaystyle R(u,v)=R_{1}(u/v,v^{2})}
∫
R
(
sin
x
,
cos
x
)
d
x
=
∫
R
1
(
tan
x
,
cos
2
x
)
d
x
=
∫
R
1
(
t
,
1
1
+
t
2
)
1
1
+
t
2
d
t
(
tan
x
=
t
)
{\displaystyle \int R(\sin x,\cos x)\mathrm {d} x=\int R_{1}(\tan x,\cos ^{2}x)\mathrm {d} x=\int R_{1}\left(t,{\frac {1}{1+t^{2}}}\right){\frac {1}{1+t^{2}}}\mathrm {d} t\qquad (\tan x=t)}
사실 모든 유리 함수는 위와 같은 세 유리 함수의 합으로 다음과 같이 나타낼 수 있다.
R
(
u
,
v
)
=
R
(
u
,
v
)
−
R
(
−
u
,
v
)
2
+
R
(
−
u
,
v
)
−
R
(
−
u
,
−
v
)
2
+
R
(
−
u
,
−
v
)
+
R
(
u
,
v
)
2
{\displaystyle R(u,v)={\frac {R(u,v)-R(-u,v)}{2}}+{\frac {R(-u,v)-R(-u,-v)}{2}}+{\frac {R(-u,-v)+R(u,v)}{2}}}
무리 함수의 부정적분은 초등 함수가 아닐 수 있다. 그러나 다음과 같은 꼴의 부정적분은 초등함수이다.
R
(
x
,
a
x
+
b
c
x
+
d
n
)
{\displaystyle R\left(x,{\sqrt[{n}]{\frac {ax+b}{cx+d}}}\right)}
여기서
R
(
u
,
v
)
{\displaystyle R(u,v)}
m
∈
Z
+
{\displaystyle m\in \mathbb {Z} ^{+}}
a
,
b
,
c
,
d
∈
R
{\displaystyle a,b,c,d\in \mathbb {R} }
a
d
−
b
c
≠
0
{\displaystyle ad-bc\neq 0}
a
x
+
b
c
x
+
d
n
=
t
,
x
=
d
t
n
−
b
a
−
c
t
n
,
d
x
=
n
(
a
d
−
b
c
)
t
n
−
1
(
a
−
c
t
n
)
2
d
t
{\displaystyle {\sqrt[{n}]{\frac {ax+b}{cx+d}}}=t,\;x={\frac {dt^{n}-b}{a-ct^{n}}},\;\mathrm {d} x={\frac {n(ad-bc)t^{n-1}}{(a-ct^{n})^{2}}}\mathrm {d} t}
그러면 원래의 부정적분은 유리 함수의 부정적분으로 변한다.
∫
R
(
x
,
a
x
+
b
c
x
+
d
n
)
d
x
=
∫
R
(
d
t
n
−
b
a
−
c
t
n
,
t
)
n
(
a
d
−
b
c
)
t
n
−
1
(
a
−
c
t
n
)
2
d
t
{\displaystyle \int R\left(x,{\sqrt[{n}]{\frac {ax+b}{cx+d}}}\right)\mathrm {d} x=\int R\left({\frac {dt^{n}-b}{a-ct^{n}}},t\right){\frac {n(ad-bc)t^{n-1}}{(a-ct^{n})^{2}}}\mathrm {d} t}
함수
(
a
+
b
z
)
p
z
q
{\displaystyle (a+bz)^{p}z^{q}}
a
,
b
∈
R
{\displaystyle a,b\in \mathbb {R} }
p
,
q
∈
Q
{\displaystyle p,q\in \mathbb {Q} }
p
,
q
,
p
+
q
{\displaystyle p,q,p+q}
p
=
r
/
s
{\displaystyle p=r/s}
q
=
r
′
/
s
′
{\displaystyle q=r'/s'}
r
,
s
,
r
′
,
s
′
∈
Z
{\displaystyle r,s,r',s'\in \mathbb {Z} }
p
∈
Z
{\displaystyle p\in \mathbb {Z} }
z
s
′
{\displaystyle {\sqrt[{s'}]{z}}}
z
s
′
=
t
{\displaystyle {\sqrt[{s'}]{z}}=t}
q
∈
Z
{\displaystyle q\in \mathbb {Z} }
a
+
b
z
s
{\displaystyle {\sqrt[{s}]{a+bz}}}
a
+
b
z
s
=
t
{\displaystyle {\sqrt[{s}]{a+bz}}=t}
p
+
q
∈
Z
{\displaystyle p+q\in \mathbb {Z} }
(
(
a
+
b
z
)
/
z
)
p
z
p
+
q
{\displaystyle ((a+bz)/z)^{p}z^{p+q}}
(
a
+
b
z
)
/
z
s
{\displaystyle \textstyle {\sqrt[{s}]{(a+bz)/z}}}
(
a
+
b
z
)
/
z
s
=
t
{\displaystyle \textstyle {\sqrt[{s}]{(a+bz)/z}}=t}
보다 일반적으로, 함수
x
m
(
a
+
b
x
n
)
p
{\displaystyle x^{m}(a+bx^{n})^{p}}
a
,
b
∈
R
{\displaystyle a,b\in \mathbb {R} }
m
,
n
,
p
∈
Q
{\displaystyle m,n,p\in \mathbb {Q} }
x
n
=
z
,
x
=
z
1
/
n
,
d
x
=
1
n
z
1
/
n
−
1
d
z
{\displaystyle x^{n}=z,\;x=z^{1/n},\;\mathrm {d} x={\frac {1}{n}}z^{1/n-1}\mathrm {d} z}
그러면 위와 같은 꼴의 함수의 부정적분으로 변한다.
∫
x
m
(
a
+
b
x
n
)
p
d
x
=
1
n
∫
(
a
+
b
z
)
p
z
(
m
+
1
)
/
n
−
1
d
z
{\displaystyle \int x^{m}(a+bx^{n})^{p}\mathrm {d} x={\frac {1}{n}}\int (a+bz)^{p}z^{(m+1)/n-1}\mathrm {d} z}
따라서
p
,
q
=
(
m
+
1
)
/
n
−
1
,
p
+
q
{\displaystyle p,q=(m+1)/n-1,p+q}
p
,
q
,
p
+
q
{\displaystyle p,q,p+q}
파프누티 체비쇼프 가 증명하였다.
초등 함수 의 부정적분은 초등 함수가 아닐 수 있다. 예를 들어, 다음과 같은 부정적분들은 초등 함수가 아니다.
(오차 함수 )
∫
e
−
x
2
d
x
{\displaystyle \int e^{-x^{2}}\mathrm {d} x}
(프레넬 함수 )
∫
sin
x
2
d
x
{\displaystyle \int \sin x^{2}\mathrm {d} x}
(삼각 적분 함수 )
∫
sin
x
x
d
x
{\displaystyle \int {\frac {\sin x}{x}}\mathrm {d} x}
(로그 적분 함수 )
∫
1
ln
x
d
x
{\displaystyle \int {\frac {1}{\ln x}}\mathrm {d} x}
∫
x
x
d
x
{\displaystyle \int x^{x}\mathrm {d} x}
∫
1
1
−
x
4
d
x
{\displaystyle \int {\frac {1}{\sqrt {1-x^{4}}}}\mathrm {d} x}



































































![{\displaystyle R\left(x,{\sqrt[{n}]{\frac {ax+b}{cx+d}}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc1ce2cc8f8f9bbd84121c010863f02cf812d584)



![{\displaystyle {\sqrt[{n}]{\frac {ax+b}{cx+d}}}=t,\;x={\frac {dt^{n}-b}{a-ct^{n}}},\;\mathrm {d} x={\frac {n(ad-bc)t^{n-1}}{(a-ct^{n})^{2}}}\mathrm {d} t}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19e1a41234ba327ad0462ba879ce6ab2b15ccbe8)
![{\displaystyle \int R\left(x,{\sqrt[{n}]{\frac {ax+b}{cx+d}}}\right)\mathrm {d} x=\int R\left({\frac {dt^{n}-b}{a-ct^{n}}},t\right){\frac {n(ad-bc)t^{n-1}}{(a-ct^{n})^{2}}}\mathrm {d} t}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4337bb3f28082b6bab23337663c025ba6411944f)








![{\displaystyle {\sqrt[{s'}]{z}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92e3632862cbf2f23f656d7aa0a8aea545d32d10)
![{\displaystyle {\sqrt[{s'}]{z}}=t}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14111933807a7880cb5e80fab91c1990c2f0e42c)

![{\displaystyle {\sqrt[{s}]{a+bz}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f6a28d18ae30f610cf3ae09b1111391463cc31e)
![{\displaystyle {\sqrt[{s}]{a+bz}}=t}](https://wikimedia.org/api/rest_v1/media/math/render/svg/803fae17b804fe612ff45b4af31000cfd00b52bc)


![{\displaystyle \textstyle {\sqrt[{s}]{(a+bz)/z}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9214214696b50be617dc58a85bc122e7e319a74)
![{\displaystyle \textstyle {\sqrt[{s}]{(a+bz)/z}}=t}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aab24390fbfb2ea114f3573f05baf7466c4fa0c6)










