힘 (물리)
| 고전역학의 역사 |

물리학에서 힘(영어: Force)은 물체의 운동, 방향 또는 구조를 변화시킬 수 있는 상호작용이다. 다르게 말하여, 힘은 질량을 가진 물체의 속도를 변화시키는 요인(이는 정지 상태에서 이동하기 시작하는 것도 포함)이며, 즉 물체를 가속시키거나 신축성이 있는 물체는 변형시킬 수 있고, 가속과 변형 둘 다 일어날 수도 있다. 또한 힘은 밀리거나 밀어내는 것이라는 직관적인 개념으로도 설명할 수 있다. 힘은 크기와 방향을 모두 가졌기 때문에 벡터량으로 표현한다. 힘은 뉴턴이라는 국제단위계로 측정되며 F라는 기호로 표현한다.
뉴턴 운동 법칙의 제2법칙의 원래 형태는 물체의 알짜힘이 미분 시간과 운동량의 변화의 곱과 같다는 형태였다.[1] 만약 물체의 질량이 일정할 경우, 이 법칙은 물체에 작용하는 알짜힘은 알짜힘의 방향에 작용하는 가속도에 비례하고 물체의 질량에 비례한다는 의미이다. 힘의 공식으로는 다음과 같이 표현된다.
기호 위의 화살표는 크기와 방향 모두를 가진 벡터량을 의미하는 기호이다.
힘과 관련된 개념으로는 다음이 있다. 먼저 추력은 물체의 속도를 증가시킨다. 항력은 물체의 속도를 감소시킨다. 돌림힘은 물체에 대한 각속도 변화를 만들어낸다. 확장된 개념의 각 부분은 일반적으로 인접한 부분에 힘을 작용시킨다. 이러한 힘의 분포는 물체의 소위 변형력을 통해 알 수 있다.[2] 압력은 이 변형력의 간단한 형태 중 하나이다. 변형력은 보통 고체 물질의 변형이나 액체 물질이 흐르는 원인이 된다.[3][4]
개념의 개발[편집]
고전 고대의 철학자들은 정역학적이고 동역학적인 물체에 관한 힘에 대해 연구했고 단순 기계를 발명했지만, 사상가 아르키메데스와 아리스토텔레스의 힘에 대한 이해는 근본적인 오류가 있었다. 이러한 부분은 때때로 마찰력과 같은 명백하게 힘이 아닌 성분에 대해 불완전히 이해하거나 자연 운동에 대한 본질과 같은 것에 대한 불충분한 결과로 인해 나타난다.[5] 이 근본적인 오류는 힘이 심지어 일정한 속도(등속도)로 운동하더라도 힘이 필요하다는 믿음이었다. 이전의 운동과 힘에 관한 오류의 대부분은 결국 아이작 뉴턴에 의해 수정되었다. 그의 수학적 통찰력으로 만들어진 뉴턴 운동 법칙은 거의 3백 년 동안 이보다 더 뛰어난 법칙이 나오지 않았다.[4] 20세기 초반에는 알버트 아인슈타인이 상대성 이론을 발표하면서 빛의 속도에 가까운 운동량을 가진 물체에 대한 제대로 된 힘의 움직임을 예측하고 중력은 관성으로 인해 생성된 힘이라는 통찰력을 가져다주었다.
현대에서는 양자역학의 기술을 이용해 빛의 속도에 가깝게 입자를 가속시킬 수 있고 입자물리학은 원자보다 작은 입자간의 힘을 설명하는 표준 모형을 만들어냈다. 표준 모형은 게이지 보손이라는 입자를 교환하여 힘을 방출 및 흡수한다는 것을 예측했다. 오직 4개의 상호 작용만이 현재 알려져 있다. 힘의 크기에 따라 나누면 다음과 같다. 강한 상호작용, 전자기력, 약한 상호작용, 중력이다.[3] 고에너지 물리학은 1970년대와 80년대 입자들의 관측 결과 약한 상호작용과 전자기력이 근본적으로는 전기·약 작용 상호작용으로 표현할 수 있다는 것을 알아냈다.[6]
뉴턴 이전 개념[편집]

고대부터 힘의 개념은 간단 기계의 기능에 중요한 역할로 인식되고 있었다. 단순 기계의 기계적 확대율은 먼 거리에서 작용되는 힘에 대해 더 적은 힘을 받기 때문에 동일한 일을 했다. 힘의 특성 분석은 궁극적으로 아리스토텔레스가 액체 고유의 부력 논의를 공식화한 것으로 유명하다.[5]
아리스토텔레스는 힘의 개념에 대해서 철학적 토론을 하였고 아리스토텔레스의 우주론의 중요한 부분이 되었다. 아리스토텔레스의 관점에서 자연은 4개 원소가 "자연 상태"를 존재하게 만든다고 봤다. 아리스토텔레스는 흙과 물 등의 원소가 지구의 질량를 이루는 물체의 기본 성질이며, 지상 위에서 움직이지 않는 물체는 기본적인 원소 상태로 돌아가려는 경향을 보인다고 믿었다. 그는 무거운 물체가 떨어지는 현상 등이 "자연적인 장소"로 찾아갈려는 본질적인 현상이라 생각했으며, 이는 자연스럽거나 인위적으로 움직이는 "자연적인 현상"을 나타내주는 지속적인 힘을 주는 지속적인 과정이 필요하다고 생각했다.[7] 이 이론으로, 수레를 움직이게 하는 힘의 상수나 화살 등의 발사체의 행동에 대한 개념에 대해 문제를 제기했고 일상적인 경험을 바탕으로 적용했다. 힘이 발사체에 작용하는 곳은 오직 비행이 시작하는 곳 뿐이며, 발사체가 공기 중을 움직이면서 어떤 식별 가능한 힘도 작용하지 않는다고 생각했다. 아리스토텔레스는 이 문제에 대해 인식하고 있었으며 공기가 발사체의 경로에서 발사체가 계속 움직일 수 있는 힘을 제공한다고 제안했다. 이 설명은 발사체가 움직이는 데에는 공기가 필요하며 진공 환경 등에서는 처음의 충격 이후 움직이지 않을 것으로 예측했다. 또한 발사체의 움직임에서 항력이라는 문제도 생기게 되었다.[8]
아리스토텔레스 물리학은 6세기 존 필로포누스(John Philoponus)에 의해 중세 과학의 비판을 받게 되었다.
아리스토텔레스 물리학의 허점은 17세기 갈릴레오 갈릴레이가 중세 후기 임페투스가 물체의 움직임을 만든다는 아이디어를 가져올 때까지 수정하지 못했다. 갈릴레이는 돌과 포탄 모두 떨어지게 하는 실험에서 17세기 초 아리스토텔레스 물리학의 중력 이론을 반증했다. 그는 물체가 중력에 의해 가속되었고 질량과는 독립적이며 속도는 마찰력 등의 힘에 의해 작용되지 못한다는 것을 증명했다.[9]
뉴턴 역학[편집]
아이작 뉴턴은 관성 및 힘의 개념을 이용하여 모든 물체의 움직임을 설명하기 위해 노력했고 그렇게 함으로써 보존 법칙을 발견했다. 1687년, 뉴턴은 자연철학의 수학적 원리라는 자신의 논문을 출간했다.[4][10] 이 논문에서는 고전역학에서 설명하는 힘의 방법으로 뉴턴의 운동에 관한 세 가지 법칙을 나열했다.[10]
뉴턴의 제 1 법칙[편집]
뉴턴의 운동 제1법칙은 물체는 외부의 알짜힘 또는 합성힘이 없을 경우 등속도로 계속 움직인다는 법칙이다.[10] 이 법칙은 갈릴레이의 통찰을 확장시켜 알짜힘의 부족과 관계되었다(이에 관한 자세한 설명은 다음 참조). 뉴턴은 질량을 가진 물체는 "정지는 자연적 상태"라는 아리스토텔레스의 아이디어 대신 "자연적 상태"라는 기본 평형을 이루는 함수인 고유의 관성이 있다고 제안했다. 즉, 제 1법칙은 직관적인 아리스토텔레스 신념에 모순되어 일정한 속도로 움직이는 개체의 속도가 유지되기 위해서는 알짜힘이 필요하다. "0이 아닌 일정한 속도"는 "정지 상태"와 물리적으로 구별되었고, 뉴턴의 1 법칙은 여기에 갈릴레이 상대성의 개념으로 관성을 연관시켰다. 특히, 물체가 서로 다른 속도로 이동하는 계에서 어떤 물체가 움직이고 있고 정지해 있는지 구별하는 것은 불가능하다. 기술적인 말로 바꾸면, 물리학의 법칙은 모든 갈릴레이 변환과 관련된 관성 좌표계에서도 동일하다는 것이다.
예를 들어, 움직이는 차에서 등속도로 주행하는 동안 물리학의 법칙은 정지 상태와 같다. 탑승한 사람은 차가 이동하는 방향으로 힘을 적용할 필요 없이 정지 상태와 같이 수직으로 공을 똑바로 던지면 받을 수 있다. 이것은 심지어는 이동하는 차의 밖에서 관찰하면서 공이 차의 움직임에 따라 포물선으로 운동하는 것처럼 보이는데도 물리 법칙은 동일하다. 이는 공에 작용하는 관성이 차량의 운동 방향과 일정하게 같은 속도로 작용하여 공을 던져도 앞으로 계속 운동할 수 있기 때문이다. 차 안에 있는 사람의 관점에서는 차량 및 내부의 모든 것이 정지 상태로 관측된다. 외부의 세계는 모두 차와 반대 방향으로 일정한 속도로 운동하는 것처럼 보인다. 실험 결과로 알 수 없기 때문에, 차량이 정지해 있는지 바깥 세계가 정지해 있는지 이 두가지 경우를 물리적으로 구별할 수 없다. 이럴 경우 정지 상태와 등속도 운동은 동등한 관성이 적용된다.
관성의 개념은 지속적인 운동 등 다양한 형태의 물체 운동 경향을 설명하기 위해 엄격하게 일정한 속도가 아니더라도 일반화할 수 있다. 지구의 관성 모멘트로 인해 날과 년의 길이 불변성이 수정되었다. 알버트 아인슈타인은 관성의 원리를 확장하여 중력을 받는 물체로 자유낙하 시킬 때 등 일정한 가속도를 받는 것과 관성을 받는 것은 물리적으로 동등하다는 뼈대를 세웠다. 이것은 예를 들어 우주비행사처럼 지구 주위의 자유 낙하 궤도에서 무중력을 체험할 경우에도 뉴턴의 운동 법칙은 이러한 환경에서도 보다 쉽게 식별할 수 있기 때문이다. 우주비행사는 자기 자신 옆의 공중에서 질량이 있는 물체를 놓을 경우 관성으로 인해 우주비행사 곁에서 고정된 채로 있다. 이는 우주비행사와 물체가 은하계 사이의 공간에서 공유하고 있는 기준점이 중력의 그물 영향 없이 발생하는 일의 경우와 같다. 이 등가원리는 일반 상대성 이론의 발명을 위한 기초 토대 중 하나이다.[11]

은 실제로는 제 2 법칙에서 미분학을 사용하지 않은 다른 형태로 적었다.
뉴턴의 제 2 법칙[편집]
뉴턴의 제 2 법칙의 현대 형태는 벡터 미분 방정식으로 표현한다.[12]
여기서 는 물체의 운동량이며, 는 알짜힘(벡터 합)이다. 둘이 같을 때 알짜 힘이 "0"으로 정의되지만, 균형을 이룬 동등한 힘으로도 존재할 수 있다. 반면, 제 2법칙은 "불균형한 힘"에 대해 말하며 물체에 작용하는 물체의 운동량은 시간이 지남에 따라 변화가 발생한다.[10]
운동량의 정의에 의해,
뉴턴의 제 2법칙은 오직 일정한 질량일 때만 적용되며,[13] 이런 이유로, m은 미분 연산자를 이용하여 밖으로 꺼낼 수 있다. 이 계산은 다음과 같다.
가속도의 정의를 대입한 뉴턴의 제 2법칙의 간단한 형태는 다음으로 파생된다.
이 공식은 때로는 "물리학에서 두 번째로 유명한 공식"으로도 불린다.[14] 뉴턴은 위 공식의 축소적인 형태를 명시적으로 언급하지 않았다.
뉴턴의 제 2법칙은 힘은 가속도에 비례하고 가속도는 질량에 반비례한다는 성질을 알려 준다. 가속도는 운동의 측정을 통해 정의할 수 있다. 그러나, 운동은 관성계에서 고급 물리학 분석을 통해 잘 설명하는 반면 여전히 질량의 정의는 무엇인지에 관한 깊은 문제가 남아 있다. 일반 상대성 이론에서는 시공간과 질량이 동등하다고 말하지만, 양자 중력에 관한 일관된 이론이 빠져 있고 미시 세계에서는 거시 세계에서 시공간을 연결하는 방법과의 관계가 불분명하다. 몇몇 타당한 이유로, 뉴턴의 제 2법칙은 등가 법칙을 이용하여 "질량의 정량적 정의"로 어느 정도 설명할 수 있다. 그리고, 질량과 힘의 상대적인 단위는 고정되어 있다.
뉴턴의 제 2법칙을 이용한 힘의 정의는 보다 엄격한 논문에서는 수학적으로는 자명한 것이기 때문에 이를 일부 받아들이지 않고 있다.[3][15] 에른스트 마흐, 크리퍼드 트루스델, 발터 놀 등의 유명한 물리학자, 철학자, 수학자들은 힘에 대한 명시적인 정의에 대해 모색하고 있다.[16]
뉴턴의 제 2법칙은 힘의 크기를 측정하는 데 이용할 수 있다. 예를 들어, 행성의 궤도 가속도에 대한 대략적인 지식으로 과학자들은 행성의 중력을 계산할 수 있다.
뉴턴의 제 3 법칙[편집]
뉴턴의 제 3법칙은 힘이 다른 곳에 있는 물체에게 영향을 줄 수 있을 때, 이의 결과로 대칭적인 현상이 발생한다는 의미이다. 제 3법칙은 모든 힘은 다른 물체 사이와 "상호작용"을 하며,[17][18] 결국 단방향으로 전달되는 힘이나 한 물체에만 작용하는 힘은 존재하지 않는다. 예를 들어, 홍길동이 옆 사람을 민다면 힘의 주체는 홍길동이고 대상은 옆 사람이다. 이때 홍길동도 옆 사람을 떠민 만큼 옆 사람도 홍길동에게 작용하는데 이를 반작용이라 한다.[19] 한 물체가 다른 물체에게 F의 힘을 가하면, 힘을 가한 물체에게는 -F의 힘이 가해진다. F와 -F는 방향만 다르고 크기는 서로 같은 힘이다. 이 법칙은 종종 F 힘에 대한 반작용으로 작용한 것이 -F라는 것으로 언급한다. 이 작용과 반작용은 동시에 존재한다.
물체 1과 물체 2가 동일한 계에 존재한다고 가정할 경우, 물체 1과 물체 2 사이 상호작용에 의한 계 내의 알짜힘은 0이 된다.
이 뜻은 입자가 닫힌 계에 존재할 경우 이 계에서 힘의 불균형에 의한 내력은 존재하지 않는다는 의미이다. 즉, 닫힌 계에서 임의의 두 물체 간에 작용-반작용 힘을 공유하면서 계의 질량중심이 이동이 되지 않는다. 계 내의 물체는 서로서로에 대해 가속받으면서 계 내에서의 합력이 0이 된다. 그 대신에, 계에서 외력이 작용할 경우 질량중심은 계의 질량을 외력으로 나눈 크기만큼 가속할 것이다.[3]
뉴턴의 제 2법칙과 제 3법칙을 결합하면, 계 내의 선운동량 보존을 설명할 수 있다.
이 식에서 시간에 대하여 적분할 경우, 방정식은 다음과 같이 변한다.
이러한 방정식에서, 물체 1과 물체 2를 포함하는 계인 경우, 다음과 같이 변한다.
이를 통해 선운동량은 보존되는 것을 증명할 수 있다.[20] 유사한 논거를 이용하여, 임의의 수의 입자가 존재하는 계로 일반화할 수 있다. 이것은 물체 사이의 운동량 교환은 계의 알짜 운동량에 영향을 주지 않는다는 것을 보여준다. 일반적으로, 모든 힘은 질량을 가진 물체에게 상호 작용을 하기 때문에 알짜 운동량이 손실되지도 얻지도 않는 계를 정의할 수 있다.[3]
성질[편집]
힘은 인력 또는 척력으로 인식하기 때문에 힘을 직관적으로 이해하기 쉽다.[4] 온도 같은 다른 개념을 통해 설명한 힘의 직관적인 이해는 직접적인 관찰과 측정이 일치하기 때문에 정확하게 조작적 정의를 사용하여 정령화하게 된다. 실험을 통해, 뉴턴 역학을 통한 힘의 이해와 측정을 통한 이해가 정확히 일치하다는 것을 밝혀냈다.
힘은 얼마나 끌거나 미는 힘이 강한가에 따른 방향과 크기에 따라 특정 행동을 한다. 이러한 특성 때문에, 힘은 유클리드 벡터로 구분한다. 이 뜻은 힘이 방향이 필요 없는 스칼라인 물리적 양과 다른 그 이상의 서로 다른 수학 규칙의 집합이라는 것이다. 예를 들어, 두 힘이 같은 물체에게 작용할 때 무슨 일이 일어날지 결정할 때, 합력을 구하기 위해서는 두 힘의 크기 및 방향을 알아야 한다. 이러한 각각의 힘에 두 정보 모두를 알고 있지 못하면 상황은 모호해진다. 예를 들어, 만약 같은 크기의 힘으로 두 사람이 밧줄을 당긴다는 것을 알지만 두 사람이 당기는 방향을 모른다면 이 줄이 어떻게 될 지 아는 것은 불가능하다. 줄다리기처럼 두 사람이 반대 방향에서 잡아당기거나 두 사람이 같은 방향에서 잡아당길 수 있다. 간단한 1차원적 예로, 힘의 방향을 모른 체 알짜 힘은 두 힘의 크기를 더하는지, 큰 쪽에서 다른 쪽을 빼야 하는지 결정할 수 없다. 벡터와 힘을 연관시키면 이런 문제를 해결할 수 있다.
역사적으로, 힘은 먼저 몇 가지 힘들이 서로를 0으로 만드는 정적 평형 상태 조건에서 조사하기 시작했다. 이러한 실험들은 힘이 벡터량을 가진다는 중요한 특성을 증명했다. 힘은 크기와 방향 모두를 갖고 있다는 것이다.[4] 점입자 위의 두 힘이 작용할 때 합력(알짜힘)은 벡터 공간에서 평행사변형 법칙으로 구한다. 두 힘의 벡터를 평행사변형의 양 변으로 하여 평행사변형의 변을 이은 끝점끼리를 이은 벡터가 합력이다.[3] 합력 크기는 두 힘 사이의 각의 크기에 따라 달라진다. 그러나, 만약 힘이 늘어난 물체에 작용하면 각각 작용하는 벡터는 반드시 물체의 움직임에 작용하는 적용되는 순서로 작용해야 한다.
자유물체도는 계 내의 힘을 알아내는 편리한 방법으로 이용할 수 있다. 이상적으로, 이 다이어그램은 힘을 벡터의 각도 및 상대적인 크기를 보존하여 그리기 때문에 벡터들 합력의 알짜힘을 구할 수 있다.[21]

서로 더할 수 있는 것 뿐이 아니라, 힘은 합력에서 서로 직각으로 독립되어 작용하는 경우로 분리하는 법을 구할 수 있다. 북동쪽을 가리키는 수평의 한 힘은 북쪽을 향하는 힘과 동쪽을 향하는 힘 두개로 분리할 수 있다. 벡터의 덧셈을 이용하여 이러한 구성 요소를 합친 힘을 원래 힘으로 구할 수 있다. 기저의 집합의 원소의 힘 벡터를 구하는 법은 크기와 방향을 이용하여 힘을 설명하는 것보다 종종 더욱 간결한 수학적 방법으로 이용하기도 한다.[22] 또 다른 예를 들면, 예를 들어 목수가 나무에 못을 박을 경우 못을 때리는 망치가 왼쪽의 그림과 같이 비스듬히 내리친다면 망치를 통해 전해지는 알짜힘(붉은색 화살표)은 수직 성분(파란색 화살표)과 수평 성분(녹색 화살표)으로 나누어 생각할 수 있다. 이 경우 알짜힘의 크기를 키우려면 망치가 못을 칠 때 정학히 수직이 되도록하여 수직성분의 힘을 키워야 할 것이다. 실제의 경우 못이 일단 나무에 박히면 망치에 편평한 면이 수직이 되게 못을 치는 것이 보다 수월해 지므로 목수들은 처음에는 약한 힘으로 망치를 사용하여 못이 나무에 자리잡게 만들고 점점 세게 쳐서 못이 잘 박히게 한다.[23] 이러한 이유로, 각 힘이 직교성을 가질 경우 각 벡터 힘의 합은 각 벡터의 스칼라 덧셈을 한 힘의 벡터 힘으로 작용한다. 직교하는 힘은 서로 직각으로 작용하는 힘이 다른 힘의 크기나 방향에 영향을 미치지 않기 때문에 독립적이다. 직교하는 기저 벡터를 선택하는 것은 기준 벡터의 집합이 수학적 계산에서 가장 편리하다는 것을 자주 고려한다. 오직 하나만 구성하는 힘을 가지고 있기 때문에, 같은 방향에 위치하는 힘을 기저 벡터로 선택하는 것이 바람직하다. 직교하는 힘 벡터는 세 번째 힘이 다른 두 힘과 직각을 이룰 수 있다.[3]
평형[편집]
평형 상태는 한 점입자에 존재하는 합력이 0일때, 즉 모든 힘 벡터의 합이 0일 때 나타난다. 확장하는 물체를 다룰 때는 순 토크가 0이라는 가정이 필요하다.
평형 상태에는 정적 평형과 동적 평형 두 가지가 존재한다.
정적 평형[편집]
정적 평형은 고전 역학의 발명 이전에 이해되었다. 정지해 있는 물체의 알짜힘은 0이라는 것이 정적 평형이다.[24]
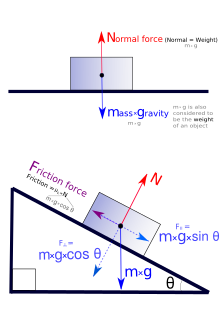
정적 평형의 간단한 경우는 두 개의 힘이 크기는 같고 방향만 다른 경우에 발생한다. 예를 들어, 물체의 표면 수준에는 중력에 의해 지구 중심을 향해 아래로(인력) 당겨지게 된다. 동시에, 표면의 힘이 아래에서 위쪽으로 동일한 크기의 힘을 가한다. 이를 수직항력이라고 한다. 이 상황은 알짜힘이 0이며 가속도가 없는 상황이다.[4]
물체를 밀 때, 표면의 마찰이 가해진 힘과 반대 방향으로 물체와 바닥 사이에 생기기 때문에 정지 마찰이라는 물체가 운동하지 않는 상황이 나타날 수 있다. 아무 움직임도 없는 상황일 때, 정지 마찰은 가속도가 없을 때 가해진 힘만큼 "정확히" 균형을 이룬다. 작용한 힘의 반응은 마찰 한계점까지 정지 마찰이 증가하거나 감소할 수 있으며, 이는 표면과 물체 사이의 접촉 특성에 따라 다르다.[4]
두 힘 사이의 정적 평형은 저울이나 용수철 저울 등 간단하게 힘을 측정하는 장치로 이용하기도 한다. 예를 들어, 물체는 수직으로 놓여 있는 용수철 저울에서 물체가 받는 중력만큼 용수철이 "용수철의 당기는 힘"을 받게 되어 물체는 움직이지 않고 균형을 이루게 된다. 이러한 도구들을 이용하여, 일부 정량적인 법칙이 발견되었다. 대표적으로, 중력은 밀도 상수에 비례한다(표준 무게 정의를 위해 널리 이용되었음), 아르키메데스의 원리를 이용한 부력의 이해, 아르키메데스의 지레 탐구, 기체에 압력에 대한 보일의 법칙, 용수철에 대한 훅의 법칙 등이 있다. 이 모든 것들은 아이작 뉴턴이 운동 제 3법칙을 강론하기 전에 실험적으로 검증되고 공식화되었다.[3][4]
동적 평형[편집]

동적 평형은 아리스토텔레스 물리학과 관측 결과 사이 논리학적 모순으로 인해 특정한 가정을 한 갈릴레오 갈릴레이가 처음으로 설명했다. 갈릴레이는 절대적인 정지 좌표계라는 개념은 갈릴레이 절대성에 의해 존재하지 않는다는 것을 깨달았다. 갈릴레이는 일정한 속도로 움직이는 것과 정지한 것은 완전히 동등한다는 결론을 내렸다. 이것은 아리스토텔레스가 말한 질량이 있는 물체는 자연스러운 상태로 다가간다는 "자연적인 상태"라는 개념에 위배되었다. 갈릴레이는 등속도와 정지 상태는 같은 상태라는 옳은 이해를 간단한 실험으로 보여주었다. 예를 들어, 만약 선원이 일정한 속도로 움직이는(등속도) 배에서 까마귀의 둥지에게 포탄을 떨어뜨릴 경우, 아리스토텔레스 물리학에서는 배가 아래로 이동하면서 포탄이 똑바로 떨어질 것이라고 생각했다. 따라서, 아리스토텔레스의 우주관에서는 떨어진 포탄은 움직이는 배 돛대의 아래 부분에 떨어지지 않을 것이라 생각했다. 그러나, 이 실험을 실제로 시행하면 포탄은 마치 포탄이 떨어졌음에도 불구하고 배와 같이 진행하여 돛대의 아래 부분에 정확히 떨어진다. 이 떨어지는 포탄에 작용하는 정방향의 수평 힘이 없기 때문에, 결론은 오직 포탄이 떨어질 때 배와 같은 속도로 계속 이동한다는 것 밖에 남지 않는다. 따라서, 배에서 떨어지는 포탄은 앞으로 계속 이동하기 위해 힘이 필요하지 않는다.[9]
또한, 등속도로 운동하는 모든 물체는 물체의 알짜힘(합력)이 0이어야 한다. 이 동적 평형의 정의는 물체의 모든 힘이 균형을 이루지만 등속도로 운동하는 것을 뜻한다.
동적 평형의 가장 간단한 경우는 물체와 표면간의 운동 마찰력을 들 수 있다. 몇몇 경우에서, 운동 마찰력은 운동할려는 힘이 작용하려는 방향과 정확히 반대 방향, 같은 크기로 적용된다. 이 결과는 알짜힘이 0이 되지만, 물체는 속도가 0이 아닌 상태에서 시작하였기 때문에 0이 아닌 속도로 계속 운동한다. 아리스토텔레스는 이러한 운동을 가해진 힘 때문에 발생하는 것으로 착각하였다. 그러나, 운동 마찰을 고려해야 할 때는 등속 운동을 일으키게 하는 원인인 알짜 힘이 없다는 것이 확실하다.[3]
특수 상대성 이론[편집]
특수 상대성 이론에서, 질량과 에너지는 물체를 가속시키는 데 필요한 양을 계산하여 알아볼 수 있듯이 동등하다. 물체의 속도를 증가시킬 때, 에너지는 질량(관성)과 등가적인 일을 수행한다. 따라서, 높은 속도에서 가속할 경우에는 낮은 속도에서 가속시켰던 양보다 가속도를 높이는 데 더욱 많은 에너지를 필요로 한다. 뉴턴의 제 2 법칙에서는
이것은 수학적인 정의이기 때문에 유효하다.[25] 그러나, 보존력을 위해 상대론적 운동량은 다음과 같이 다시 정리해야 한다.
이 식에서
입자의 상대론적 표현과 관련된 힘과 가속도는 0이 아닌 불변 질량 상수 을 수학적으로 방향으로 이동시키며 결과는 다음과 같다.
여기서 로런츠 인자는 다음과 같다.
상대성 이론의 초기에 과 라는 표현은 횡방향 질량과 종방향 질량으로 불렸다. 상대론적 힘은 일정한 가속도를 만들지 않지만, 물체의 감속 가속도는 빛의 속도에 근접한다. 는 광속으로 운동하는 불변 질량이 0이 아닌 물체일 경우 0으로 나누기로 산출하게 되며, 이론상으로는 속도를 전혀 예측할 수 없게 된다.
그러나, 한 형태는 다음과 같이 되찾을 수 있다.
상대성 이론은 여러 상수에서 사차원 벡터의 사용을 통해 연관관계를 설명한다. 이 관계는 가 사차원 힘이고, 가 불변 질량이며, 가 사차원 가속도일 때 상대성 이론에서 정확하게 성립한다.[27]
파인먼 도형[편집]

현대 입자물리학에서, 힘과 입자의 가속도는 게이지 보손의 운동량 운반 교환 작용을 통해 수학적으로 설명하고 있다. 양자장론과 일반 상대성 이론의 발달로 인해 힘에서 운동량 보존이 발생하는 현상을 두 이론을 통해 중복해서 설명하는 데 성공했다(상대성 이론의 사차원 운동량과 양자 전기역학에서 가상 입자의 운동량). 운동량 보존은 공간에서 직접적으로 균질하게 나타나는 현상이며(이를 대칭성이라고 함), 이로 인해 힘보다 더욱 근본적인 개념에 속한 것으로 간주한다. 따라서, 현재까지 알려진 기본 힘은 정확하게 기본 상호작용이라고 말한다.[6] 입자 A가 가상의 입자 B를 방출(생성)하거나 흡수(소멸)할 때 운동량 보존은 B를 통해 A와 A' 사이 인력이나 척력을 주고받는 매개체로 활동한다. 이 설명은 기본 상호작용에서 발생하는 모든 힘에 적용된다. 정교한 수학적 설명을 예측하는 것은 상새히 하면 이러한 상호작용의 정확한 결과는 파인만 도형을 통해 개념적으로 상호작용을 간단히 설명할 수 있다. 파인만 도형에서 각각의 입자는 직선(세계선)으로 표현하며 일반적으로 이 도형에서 위로 가는 선(y축)이 시간의 흐름을 의미한다. 물질과 반물질 입자는 파인만 도형에서 진행하는 방향만 제외하고 같은 입자이다. 입자의 세계선은 상호작용 정점에서 교차하며, 파인만 도형에서 상호작용으로 인해 나타나는 힘은 입자의 세계선 방향에서 정점이 발생하는 순간과 연결되어 있다. 게이지 보손은 정점에서 물결 모양의 선으로 방출하는 모양을 그리며, 가상 입자의 교환일 경우 인접한 정점으로 흡수하는 모향으로 그려진다.[28]
파인만 도형의 유용성은 기본 상호작용의 일반적인 부분이지만 개념적으로 힘이 분리될 때와 같은 물리학의 다른 유형의 현상들도 동일한 규칙을 이용하여 설명할 수 있다는 것이다. 예를 들어, 파인만 도형은 중성자의 베타 붕괴로 양성자, 전자, 중성미자가 되는 과정인 게이지 보존을 통한 약한 상호작용을 간결하게 자세히 설명할 수 있다.[28]
기본 모델[편집]
우주의 모든 힘은 4가지 기본 상호작용으로 표현한다. 강한 상호작용과 약한 상호작용은 매우 짧은 거리에서만 작용하며, 핵자와 원자핵 사이의 결합을 포함한 아원자 입자 사이에서 강한 상호작용을 한다. 전자기력은 전하 사이에서 작용하며 중력은 질량이 있는 물체 사이에서 작용한다. 다른 모든 힘은 이 4가지 기본 상호작용에 바탕을 두고 있다. 예를 들어, 마찰력은 두 면의 원자 사이에서 발생하는 전자기학적 힘 작용의 결과이며, 파울리 배타 원리[29] 가 원자들이 서로 통과하지 못하도록 막는 역할을 한다. 훅 법칙으로 모델링한 용수철의 힘은 전자기력 작용의 결과이며 파울리 배타 원리에 따라 물체가 평형 위치로 오게끔 작용하는 역할을 한다. 원심력은 가속력으로 기준계의 회전가속으로 간단하게 일어난다.[3]
힘의 기본적 이론 개발은 서로 다른 힘을 하나로 뭉친다는 통일장 이론으로 진행되었다. 예를 들어, 아이작 뉴턴은 지구 표면으로 떨어지는 물체가 받는 힘과 천체에 관한 중력에 대한 보편적인 이론을 자신의 이론으로 통일했다. 마이클 패러데이와 제임스 클러크 맥스웰은 전자력과 자기력을 20세기에 전자기력이라는 하나의 일관된 이론으로 통일할 수 있음을 보여주었고, 양자역학의 개발로 현대에는 중력을 제외한 3가지 힘을 물질 간 게이지 보존이라는 가상 입자의 교환을 통한 페르미온의 발현이라는 현상으로 통합하였다.[30] 이 입자물리학의 표준 모형은 힘 사이의 관계를 상정하고 과학자들은 연속적 관찰을 통해 전자기력과 약한 상호작용이 전기·약 작용으로 통합할 수 있다는 것을 확인하였다. 표준 모형은 힉스 메커니즘은 아직 완전하게 관측되진 않았고, 중성미자 진동 등 표준 모형으로 설명되지 않은 현상이 나타나는 등 완전히 정립되지 못했다. 강력과 전약력 사이의 관계를 설명하는 대통일 이론은 초대칭 등의 물리학의 미해결 문제를 일부 수용할 수 있는 후보적 이론으로 간주되고 있다. 물리학자들은 4가지 기본 상호 작용을 연관지어 설명하는 모든 것의 이론에 관한 일관된 모델을 개발하기 위해 노력하고 있다. 아인슈타인은 이러한 노력을 해결하는 덴 실패했지만, 현재 이 이론에 관한 가장 유력한 설명은 끈 이론이다.[6]
단위[편집]
힘의 SI 유도 단위는 뉴턴(N)이다. 1 뉴턴은 1 kg의 질량을 갖는 물체를 1 m/s2의 가속도로 가속시킬 수 있는 힘이다. 식으로 쓰면 다음과 같다.
간혹 CGS 단위인 다인(dy)을 쓰기도 한다. 1다인은 10만분의 1 뉴턴이다.
힘의 3요소[편집]
힘의 작용은 그 크기만으로는 결정되지 않는다. 예를 들면, 끈으로 매단 모래 주머니의 중심 가까이를 때리는 것과 상부 가까이를 때리는 것은 모래 주머니의 움직임이 각기 다르다. 즉, 힘의 크기 외에도 힘이 물체의 어느 점에, 어느 방향으로 작용하느냐에 따라서 그 효과가 다르다. 따라서 힘을 나타내려면 힘의 크기, 힘의 방향(힘의 작용선), 힘이 미치는 점(작용점)의 세 가지를 지정해야 한다. 이를 힘의 3요소라고 한다.
같이 보기[편집]
참조[편집]
- ↑ See for example pages 9-1 and 9-2 of Feynman, Leighton and Sands (1963).
- ↑ “glossary”. 《Earth Observatory》. NASA. 2008년 4월 11일에 원본 문서에서 보존된 문서. 2008년 4월 9일에 확인함.
Force: Any external agent that causes a change in the motion of a free body, or that causes stress in a fixed body.
- ↑ 가 나 다 라 마 바 사 아 자 차 e.g. Feynman, R. P.; Leighton, R. B.; Sands, M. (1963). 《Lectures on Physics, Vol 1》. Addison-Wesley.; Kleppner, Daniel; Robert Kolenkow (1973). 《An Introduction to Mechanics》. McGraw-Hill. 133–134쪽. ISBN 0-07-035048-5..
- ↑ 가 나 다 라 마 바 사 아 University Physics, Sears, Young & Zemansky, pp.18–38
- ↑ 가 나 Heath, T.L. “The Works of Archimedes (1897). The unabridged work in PDF form (19 MB)”. Archive.org. 2007년 10월 14일에 확인함.
- ↑ 가 나 다 Weinberg, S. (1994). Dreams of a Final Theory. Vintage Books USA. ISBN 0-679-74408-8
- ↑ Lang, Helen The Order of Nature in Aristotle's Physics: Place and the Elements (1998)
- ↑ Hetherington, Norriss S. (1993). 《Cosmology: Historical, Literary, Philosophical, Religious, and Scientific Perspectives》. Garland Reference Library of the Humanities. 100쪽. ISBN 0-8153-1085-4.
- ↑ 가 나 Drake, Stillman (1978). Galileo At Work. Chicago: University of Chicago Press. ISBN 0-226-16226-5
- ↑ 가 나 다 라 Newton, Isaac (1999). 《The Principia Mathematical Principles of Natural Philosophy》. Berkeley: University of California Press. ISBN 0-520-08817-4. This is a recent translation into English by I. Bernard Cohen and Anne Whitman, with help from Julia Budenz
- ↑ DiSalle, Robert (2002년 3월 30일). “Space and Time: Inertial Frames”. 《Stanford Encyclopedia of Philosophy》. 2008년 3월 24일에 확인함.
- ↑ 뉴턴의 수학 원리에서는 "충격량"에 따른 유한 차분 방정식으로 표현했다.
- ↑ Halliday; Resnick. 《Physics》 1. 199쪽. ISBN 0-471-03710-9.
It is important to note that we cannot derive a general expression for Newton's second law for variable mass systems by treating the mass in F = dP/dt = d(Mv) as a variable. [...] We can use F = dP/dt to analyze variable mass systems only if we apply it to an entire system of constant mass having parts among which there is an interchange of mass.
[Emphasis as in the original] - ↑ For example, by Rob Knop PhD in his Galactic Interactions blog on 2007년 2월 26일 at 9:29 a.m. scienceblogs.com Archived 2012년 1월 14일 - 웨이백 머신
- ↑ One exception to this rule is: Landau, L. D.; Akhiezer, A. I.; Lifshitz, A. M. (1967). 《General Physics; mechanics and molecular physics》 Fir English판. Oxford: Pergamon Press. ISBN 0-08-003304-0. Translated by: J. B. Sykes, A. D. Petford, and C. L. Petford. Library of Congress Catalog Number 67-30260. In section 7, pages 12–14, this book defines force as dp/dt.
- ↑ e.g. W. Noll, "On the Concept of Force", in part B of Walter Noll's website..
- ↑ C. Hellingman (1992). “Newton's third law revisited”. 《Phys. Educ.》 27 (2): 112–115. Bibcode:1992PhyEd..27..112H. doi:10.1088/0031-9120/27/2/011.
Quoting Newton in the Principia: It is not one action by which the Sun attracts Jupiter, and another by which Jupiter attracts the Sun; but it is one action by which the Sun and Jupiter mutually endeavour to come nearer together.
- ↑ Resnick and Halliday (1977). 《Physics》 Thi판. John Wiley & Sons. 78–79쪽.
Any single force is only one aspect of a mutual interaction between two bodies.
- ↑ 한국물리학회 (2008). 〈제1장 힘이라고 다 같은가?〉. 《힘과 운동 뛰어넘기(속보이는 물리)》. 동아사이언스.
- ↑ Dr. Nikitin (2007). “Dynamics of translational motion”. 2009년 9월 11일에 원본 문서에서 보존된 문서. 2008년 1월 4일에 확인함.
- ↑ “Introduction to Free Body Diagrams”. 《Physics Tutorial Menu》. University of Guelph. 2008년 1월 16일에 원본 문서에서 보존된 문서. 2008년 1월 2일에 확인함.
- ↑ Henderson, Tom (2004). “The Physics Classroom”. 《The Physics Classroom and Mathsoft Engineering & Education, Inc.》. 2008년 1월 1일에 원본 문서에서 보존된 문서. 2008년 1월 2일에 확인함.
- ↑ 렌 피셔 (2006). 《슈퍼마켓 물리학》. 강윤제 역. 시공사. 98 - 99쪽.
- ↑ “Static Equilibrium”. 《Physics Static Equilibrium (forces and torques)》. University of the Virgin Islands. 2007년 10월 19일에 원본 문서에서 보존된 문서. 2008년 1월 2일에 확인함.
- ↑ Cutnell. 《Physics, Sixth Edition》. John Wiley & Sons Inc. 855–876쪽. ISBN 0-471-23124-X.
- ↑ “Seminar: Visualizing Special Relativity”. 《The Relativistic Raytracer》. 2008년 1월 4일에 확인함.
- ↑ Wilson, John B. “Four-Vectors (4-Vectors) of Special Relativity: A Study of Elegant Physics”. 《The Science Realm: John's Virtual Sci-Tech Universe》. 2009년 6월 26일에 원본 문서에서 보존된 문서. 2008년 1월 4일에 확인함.
- ↑ 가 나 Shifman, Mikhail (1999). 《ITEP lectures on particle physics and field theory》. World Scientific. ISBN 981-02-2639-X.
- ↑ Nave, R. “Pauli Exclusion Principle”. 《HyperPhysics*****Quantum Physics》. 2008년 1월 2일에 확인함.
- ↑ “Fermions & Bosons”. 《The Particle Adventure》. 2007년 12월 18일에 원본 문서에서 보존된 문서. 2008년 1월 4일에 확인함.
각주[편집]
- Corbell, H.C.; Philip Stehle (1994). 《Classical Mechanics p 28,》. New York: Dover publications. ISBN 0-486-68063-0.
- Cutnell, John d.; Johnson, Kenneth W. (2004). 《Physics, Sixth Edition》. Hoboken, NJ: John Wiley & Sons Inc. ISBN 041-44895-8
|isbn=값 확인 필요: length (도움말). - Ekbert, Hering; Rolf Martin; Martin Stohrer; Hanno Käß; Günther Kurz; Wolfgang Schulz (2017). 《Physik für Ingenieure》 12판. Köngen, Deutschland: Springer Vieweg. ISBN 978-3-662-49354-0.
- Feynman, R. P.; Leighton, R. B.; Sands, M. (1963). 《Lectures on Physics, Vol 1》. Addison-Wesley. ISBN 0-201-02116-1.
- Gutierrez, Cayetano (2017). 《Fisiquotidianía : la física de la vida cotidiana》 2판. Murcia, España: Academia de las Ciencias de la Región de Murcia. ISBN 978-8-461-14959-9.
- Halliday, David; Robert Resnick; Kenneth S. Krane (2001). 《Physics v. 1》. New York: John Wiley & Sons. ISBN 0-471-32057-9.
- Parker, Sybil (1993). 《Encyclopedia of Physics, p 443,》. Ohio: McGraw-Hill. ISBN 0-07-051400-3.
- Romeni, Claudio (2017). 《Fisica e realtà.blu. Per le Scuole superiori.》 2판. Milano, Italia: Zanichelli. ISBN 978-8-808-22113-1.
- Sánchez del Río, Carlos (2017). 《Física cuántica》 6판. Madrid, España: Piramide. ISBN 978-8-436-83679-0.
- Sears F., Zemansky M. & Young H. (1982). 《University Physics》. Reading, MA: Addison-Wesley. ISBN 0-201-07199-1.
- Serway, Raymond A. (2003). 《Physics for Scientists and Engineers》. Philadelphia: Saunders College Publishing. ISBN 0-534-40842-7.
- Tipler, Paul (2004). 《Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics》 5판. W. H. Freeman. ISBN 0-7167-0809-4.
- Verma, H.C. (2004). 《Concepts of Physics Vol 1.》 2004 Reprint판. Bharti Bhavan. ISBN 81-7709-187-5.
외부 링크[편집]
- Video lecture on Newton's three laws by Walter Lewin from MIT OpenCourseWare
- 힘의 벡터 덧셈에 관한 자바 시뮬레이션 (영어)
- Force demonstrated as any influence on an object that changes the object's shape or motion


































