코리올리 효과 (Coriolis effect)는 전향력 또는 코리올리 힘 (Coriolis force)이라고도 하며, 회전하는 계에서 느껴지는 관성력 으로, 1835년 프랑스의 과학자 코리올리 가 처음 설명해 냈다.
F
C
o
r
i
o
l
i
s
=
2
m
(
v
×
Ω
)
{\displaystyle \mathbf {F_{Coriolis}} =2m\left(\mathbf {v} \times \mathbf {\Omega } \right)}
굵은 글꼴은 그 물리량이 벡터 라는 점을 나타내고, m은 질량 , v 는 물체의 계에서의 속도 를, Ω 는 계가 돌고 있는 각속도 를 나타낸다.
코리올리 효과 [ 편집 ] 그림 1:각운동량 보존법칙에 의해 회전판의 붉은 점에서 보았을 때 물체는 진행방향의 왼쪽으로 움직이는 것처럼 보인다. 코리올리 힘의 발생원인은 각운동량 보존법칙에 의해 발생한다. 각운동량 보존법칙은 각운동량이 시간에 대해 일정하다는 것을 말한다.
만약 어떤 원점을 기준으로 계 에 돌림힘이 작용하지 않으면
d
L
d
t
=
0
{\displaystyle {\frac {d\mathbf {L} }{dt}}=0}
이 되어 각운동량이 보존되게 된다. 이를 각운동량 보존법칙 각운동량보존
회전하는 좌표계 내에서 물체가 운동을 하는 경우 회전축에 대해 반지름이 줄어드는 경우에는 줄어드는 반지름에 대해 속도가 변화하게 된다. 이 결과 회전좌표계는 코리올리힘과, 가로힘이 발생한다.
F
C
o
r
i
o
l
i
s
=
2
m
(
v
×
Ω
)
{\displaystyle \mathbf {F_{Coriolis}} =2m\left(\mathbf {v} \times \mathbf {\Omega } \right)}
발생원인 [ 편집 ] 회전 좌표계 [ 편집 ] 회전좌표계 [ 편집 ] 좌표계 x, y, z와 좌표계 x', y', z'을 보자 두 좌표계의 원점은 같다. 각각의 경우에 대해 벡터
r
{\displaystyle \mathbf {r} }
r
=
x
x
^
+
y
y
^
+
z
z
^
{\displaystyle \mathbf {r} =x{\hat {x}}+y{\hat {y}}+z{\hat {z}}}
r
=
x
′
x
^
′
+
y
′
y
^
′
+
z
′
z
^
′
{\displaystyle \mathbf {r} =x'{\hat {x}}'+y'{\hat {y}}'+z'{\hat {z}}'}
x
′
,
x
^
′
,
x
^
{\displaystyle \ x',{\hat {x}}',{\hat {x}}}
y
′
,
y
^
′
,
y
^
{\displaystyle \ y',{\hat {y}}',{\hat {y}}}
z
′
,
z
^
′
,
z
^
{\displaystyle \ z',{\hat {z}}',{\hat {z}}}
r
x
^
=
x
=
(
x
′
x
^
′
+
y
′
y
^
′
+
z
′
z
^
′
)
(
x
^
)
=
x
′
(
x
^
′
x
^
)
+
y
′
(
y
^
′
x
^
)
+
z
′
(
z
^
′
x
^
)
{\displaystyle \mathbf {r} {\hat {x}}=x=(x'{\hat {x}}'+y'{\hat {y}}'+z'{\hat {z}}')({\hat {x}})=x'({\hat {x}}'{\hat {x}})+y'({\hat {y}}'{\hat {x}})+z'({\hat {z}}'{\hat {x}})}
r
y
^
=
y
=
(
x
′
x
^
′
+
y
′
y
^
′
+
z
′
z
^
′
)
(
y
^
)
=
x
′
(
x
^
′
y
^
)
+
y
′
(
y
^
′
y
^
)
+
z
′
(
z
^
′
y
^
)
{\displaystyle \mathbf {r} {\hat {y}}=y=(x'{\hat {x}}'+y'{\hat {y}}'+z'{\hat {z}}')({\hat {y}})=x'({\hat {x}}'{\hat {y}})+y'({\hat {y}}'{\hat {y}})+z'({\hat {z}}'{\hat {y}})}
r
z
^
=
z
=
(
x
′
x
^
′
+
y
′
y
^
′
+
z
′
z
^
′
)
(
z
^
)
=
x
′
(
x
^
′
z
^
)
+
y
′
(
y
^
′
z
^
)
+
z
′
(
z
^
′
z
^
)
{\displaystyle \mathbf {r} {\hat {z}}=z=(x'{\hat {x}}'+y'{\hat {y}}'+z'{\hat {z}}')({\hat {z}})=x'({\hat {x}}'{\hat {z}})+y'({\hat {y}}'{\hat {z}})+z'({\hat {z}}'{\hat {z}})}
으로 표현되는 것을 확인할 수 있다.
회전하는 벡터의 속도 [ 편집 ] 그림 : 회전하는 좌표계에서 벡터. 벡터
A
{\displaystyle \mathbf {A} }
Ω
{\displaystyle \mathbf {\Omega } }
A
{\displaystyle \mathbf {A} }
v
=
d
A
d
t
{\displaystyle \mathbf {v} ={\frac {d\mathbf {A} }{dt}}}
d
A
d
t
=
Ω
×
A
{\displaystyle {\frac {d\mathbf {A} }{dt}}=\mathbf {\Omega } \times \mathbf {A} }
|
d
A
d
t
|
=
|
Ω
×
A
|
=
w
A
sin
θ
{\displaystyle |{\frac {d\mathbf {A} }{dt}}|=|\mathbf {\Omega } \times \mathbf {A} |=wA\sin \theta }
회전하는 좌표계에서 벡터의 속도와 가속도 [ 편집 ] 회전하는 좌표계에서 벡터의 속도 [ 편집 ] 회전좌표계의 경우에는 원점을 기준으로 좌표축 x', y', z' 이 회전하는 것으로 생각할 수 있다. 좌표계가 서로 다른 경우 두 좌표계에서 상대적인 속도는 다음과 같다.
d
A
d
t
=
d
A
′
d
t
+
V
{\displaystyle {\frac {d\mathbf {A} }{dt}}={\frac {d\mathbf {A'} }{dt}}+V}
=
v
′
+
V
{\displaystyle =\mathbf {v'} +V}
=
A
x
′
˙
x
′
^
+
A
y
′
˙
y
′
^
+
A
z
′
˙
z
′
^
+
A
x
′
d
x
^
′
d
t
+
A
y
′
d
y
^
′
d
t
+
A
z
′
d
z
^
′
d
t
{\displaystyle =\mathbf {\dot {A_{x}'}} {\hat {\mathbf {x'} }}+\mathbf {\dot {A_{y}'}} {\hat {\mathbf {y'} }}+\mathbf {\dot {A_{z}'}} {\hat {\mathbf {z'} }}+\mathbf {A_{x}'} {\frac {d\mathbf {{\hat {x}}'} }{dt}}+\mathbf {A_{y}'} {\frac {d\mathbf {{\hat {y}}'} }{dt}}+\mathbf {A_{z}'} {\frac {d\mathbf {{\hat {z}}'} }{dt}}}
이를 바탕으로 회전좌표계에서 x', y', z'의 단위벡터의 회전을 적용하여 표현하면 다음과 같다.
d
A
d
t
=
d
′
A
d
t
+
A
x
′
(
Ω
×
x
^
′
)
+
A
y
′
(
Ω
×
y
^
′
)
+
A
z
′
(
Ω
×
z
^
′
)
{\displaystyle {\frac {d\mathbf {A} }{dt}}={\frac {d'\mathbf {A} }{dt}}+\mathbf {A_{x}'} (\mathbf {\Omega } \times \mathbf {{\hat {x}}'} )+\mathbf {A_{y}'} (\mathbf {\Omega } \times \mathbf {{\hat {y}}'} )+\mathbf {A_{z}'} (\mathbf {\Omega } \times \mathbf {{\hat {z}}'} )}
=
d
′
A
d
t
+
Ω
×
(
A
x
′
x
^
′
+
A
y
′
y
^
′
+
A
z
′
z
^
′
)
{\displaystyle ={\frac {d'\mathbf {A} }{dt}}+\mathbf {\Omega } \times (\mathbf {A_{x}'} \mathbf {{\hat {x}}'} +\mathbf {A_{y}'} \mathbf {{\hat {y}}'} +\mathbf {A_{z}'} \mathbf {{\hat {z}}'} )}
=
d
′
A
d
t
+
Ω
×
A
{\displaystyle ={\frac {d'\mathbf {A} }{dt}}+\mathbf {\Omega } \times \mathbf {A} }
회전하는 좌표계에서 벡터의 가속도 [ 편집 ] 축의 회전에 따른 속도는
d
A
d
t
=
d
′
A
d
t
+
Ω
×
A
{\displaystyle {\frac {d\mathbf {A} }{dt}}={\frac {d'\mathbf {A} }{dt}}+\mathbf {\Omega } \times \mathbf {A} }
d
2
A
d
t
2
=
d
d
t
(
d
′
A
d
t
+
Ω
×
A
)
{\displaystyle {\frac {d^{2}\mathbf {A} }{dt^{2}}}={\frac {d}{dt}}({\frac {d'\mathbf {A} }{dt}}+\mathbf {\Omega } \times \mathbf {A} )}
=
d
d
t
(
d
′
A
d
t
)
+
Ω
×
d
A
d
t
+
d
Ω
d
t
×
A
{\displaystyle ={\frac {d}{dt}}({\frac {d'\mathbf {A} }{dt}})+\mathbf {\Omega } \times {\frac {d\mathbf {A} }{dt}}+{\frac {d\mathbf {\Omega } }{dt}}\times \mathbf {A} }
=
d
′
2
A
d
t
2
+
Ω
×
d
′
A
d
t
+
Ω
×
(
d
′
A
d
t
+
Ω
×
A
)
+
d
Ω
d
t
×
A
{\displaystyle ={\frac {d'^{2}\mathbf {A} }{dt^{2}}}+\mathbf {\Omega } \times {\frac {d'\mathbf {A} }{dt}}+\mathbf {\Omega } \times ({\frac {d'\mathbf {A} }{dt}}+\mathbf {\Omega } \times \mathbf {A} )+{\frac {d\mathbf {\Omega } }{dt}}\times \mathbf {A} }
=
d
′
2
A
d
t
2
+
2
Ω
×
d
′
A
d
t
+
Ω
×
(
Ω
×
A
)
+
d
Ω
d
t
×
A
{\displaystyle ={\frac {d'^{2}\mathbf {A} }{dt^{2}}}+2\mathbf {\Omega } \times {\frac {d'\mathbf {A} }{dt}}+\mathbf {\Omega } \times (\mathbf {\Omega } \times \mathbf {A} )+{\frac {d\mathbf {\Omega } }{dt}}\times \mathbf {A} }
코리올리 정리 및 코리올리 힘 [ 편집 ] 코리올리 힘 [ 편집 ] 뉴턴 의 운동방정식 이 x, y, z 좌표계 에서 성립한다고 가정하면 x', y', z' 좌표계에서 아래의 식을 만족한다.
F
=
m
d
′
2
r
d
t
2
+
2
m
Ω
×
d
′
r
d
t
+
m
Ω
×
(
Ω
×
r
)
+
m
d
Ω
d
t
×
r
{\displaystyle \mathbf {F} =m{\frac {d'^{2}\mathbf {r} }{dt^{2}}}+2m\mathbf {\Omega } \times {\frac {d'\mathbf {r} }{dt}}+m\mathbf {\Omega } \times (\mathbf {\Omega } \times \mathbf {r} )+m{\frac {d\mathbf {\Omega } }{dt}}\times \mathbf {r} }
우변의 둘째, 셋째 그리고 넷째 항을 왼쪽으로 옮기면 뉴턴의 운동 방정식과 비슷한 꼴의 운동방정식이 된다.
m
d
′
2
r
d
t
2
=
F
−
2
m
Ω
×
d
′
r
d
t
−
m
Ω
×
(
Ω
×
r
)
−
m
d
Ω
d
t
×
r
{\displaystyle m{\frac {d'^{2}\mathbf {r} }{dt^{2}}}=\mathbf {F} -2m\mathbf {\Omega } \times {\frac {d'\mathbf {r} }{dt}}-m\mathbf {\Omega } \times (\mathbf {\Omega } \times \mathbf {r} )-m{\frac {d\mathbf {\Omega } }{dt}}\times \mathbf {r} }
오른쪽 둘째 항은 코리올리 힘(Coriolis Force)이라고 부른다. 그리고 오른쪽 셋째 항은 원심력(Centripetal Force)이라고 한다. 마지막 항은 가로 힘(Transverse Force)이며 회전 각속도가 일정하지 않은 경우에만 나타난다. 원심력과 코리올리 힘을 도입한다면, 회전하고 있는 좌표계에 대한 운동방정식은 고정된 좌표계에 대해서 같다. 그리고 원심력과 코리올리 힘은 실제 힘이 아니라 회전하고 있는 좌표계에서 나타나는 가상의 힘(Fictitious Force)이다.
코리올리 힘의 예 [ 편집 ] 북반구에서의 바람의 우측편향 [ 편집 ] 그림 3: 북반구에서 저기압의 경우 코리올리 힘에 의해 바람은 진행방향에 대해 오른쪽으로 편향하게 되고 이로 인해 저기압에서는 반시계방향으로 토크가 발생하게 된다. 이 때문에 저기압에서 바람은 반시계방향으로 불게 된다. 그림4 : 북반구 저기압에서의 바람 방향은 반시계방향이다. 적도에서 북풍이 부는 경우에도 바람은 코리올리 힘을 받게 된다. 코리올리 힘은 다음과 같은 공식에 의해 계산된다.
−
2
m
Ω
×
d
′
r
d
t
{\displaystyle -2m\mathbf {\Omega } \times {\frac {d'\mathbf {r} }{dt}}}
지구는 자전 축을 중심으로
Ω
{\displaystyle \mathbf {\Omega } }
d
′
r
d
t
{\displaystyle {\frac {d'\mathbf {r} }{dt}}}
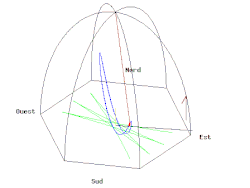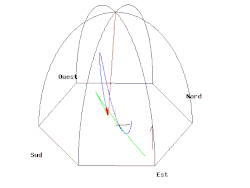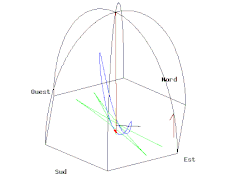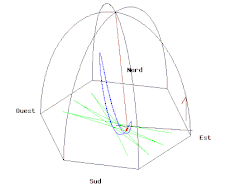
푸코의 진자 [ 편집 ] 푸코의 진자.
w
{\displaystyle \mathbf {w} }
코리올리의 힘이 적용되는 또 다른 예는 푸코의 진자 이다. 푸코의 진자는 어떤 수직면에서 자유롭게 흔들리는 줄에 매단 추이다. 진자는 정확한 수직면에서 흔들리기 시작하는데, 진동하는 수직축에 대해 몇 시간의 주기 동안 천천히 옆돌기를 한다. 진자가 긴 시간의 주기동안에 자유로이 계속하여 흔들릴 수 있도록, 추는 무거운 것으로 하고 줄은 아주 길게 한다.
질량 m인 흔들이 추의 운동의 중심을 원점으로 택하고, 이때 벡터
r
{\displaystyle \mathbf {r} }
Ω
{\displaystyle \mathbf {\Omega } }
τ
{\displaystyle \mathbf {\tau } }
g
e
=
g
−
m
Ω
×
(
Ω
×
r
)
{\displaystyle \mathbf {g_{e}} =\mathbf {g} -m\mathbf {\Omega } \times (\mathbf {\Omega } \times \mathbf {r} )}
m
d
′
2
r
d
t
2
=
τ
+
m
g
e
−
2
m
Ω
×
d
′
r
d
t
{\displaystyle m{\frac {d'^{2}\mathbf {r} }{dt^{2}}}=\mathbf {\tau } +m\mathbf {g_{e}} -2m\mathbf {\Omega } \times {\frac {d'\mathbf {r} }{dt}}}
코리올리 힘에 의해 진자는 수평방향으로 일정한 각속도
w
{\displaystyle \mathbf {w} }
z
^
{\displaystyle \mathbf {\hat {z}} }
w
{\displaystyle \mathbf {w} }
d
″
d
t
{\displaystyle {\frac {d''}{dt}}}
d
′
r
d
t
{\displaystyle {\frac {d'\mathbf {r} }{dt}}}
d
″
r
d
t
{\displaystyle {\frac {d''r}{dt}}}
d
′
r
d
t
=
d
″
r
d
t
+
w
z
^
×
r
{\displaystyle {\frac {d'\mathbf {r} }{dt}}={\frac {d''\mathbf {r} }{dt}}+\mathbf {w} \mathbf {\hat {z}} \times \mathbf {r} }
d
′
2
r
d
t
2
=
d
″
r
d
t
+
w
2
z
^
×
(
z
^
×
r
)
+
2
w
z
^
×
d
″
r
d
t
{\displaystyle {\frac {d'^{2}\mathbf {r} }{dt^{2}}}={\frac {d''\mathbf {r} }{dt}}+\mathbf {w^{2}} \mathbf {\hat {z}} \times (\mathbf {\hat {z}} \times \mathbf {r} )+2\mathbf {w} \mathbf {\hat {z}} \times {\frac {d''\mathbf {r} }{dt}}}
이를 추의 운동방정식에 적용하면 다음과 같은 식이 된다.
각속도
w
{\displaystyle \mathbf {w} }
d
″
2
r
d
t
2
=
τ
+
m
g
e
−
−
2
m
Ω
×
(
d
″
r
d
t
+
w
z
^
×
r
)
−
2
m
w
2
z
^
×
(
z
^
×
r
)
−
2
m
w
2
z
^
×
d
′
r
d
t
{\displaystyle {\frac {d''^{2}\mathbf {r} }{dt^{2}}}=\mathbf {\tau } +m\mathbf {g_{e}} --2m\mathbf {\Omega } \times ({\frac {d''\mathbf {r} }{dt}}+\mathbf {w} \mathbf {\hat {z}} \times \mathbf {r} )-2m\mathbf {w^{2}} \mathbf {\hat {z}} \times (\mathbf {\hat {z}} \times \mathbf {r} )-2m\mathbf {w^{2}} \mathbf {\hat {z}} \times {\frac {d'\mathbf {r} }{dt}}}
=
τ
+
m
g
e
−
2
m
w
z
^
×
(
z
^
×
r
)
−
m
w
2
z
^
×
(
z
^
×
r
)
−
2
m
(
Ω
+
z
^
w
)
×
(
d
″
r
d
t
)
{\displaystyle =\mathbf {\tau } +m\mathbf {g_{e}} -2m\mathbf {w} \mathbf {\hat {z}} \times (\mathbf {\hat {z}} \times \mathbf {r} )-m\mathbf {w^{2}} \mathbf {\hat {z}} \times (\mathbf {\hat {z}} \times \mathbf {r} )-2m(\mathbf {\Omega } +\mathbf {\hat {z}} \mathbf {w} )\times ({\frac {d''\mathbf {r} }{dt}})}
=
τ
+
m
g
e
−
m
(
2
w
Ω
r
)
+
w
2
z
^
r
)
z
^
+
m
(
2
w
z
^
Ω
+
w
2
)
r
−
2
m
(
Ω
+
z
^
w
)
×
d
″
r
d
t
{\displaystyle =\mathbf {\tau } +m\mathbf {g_{e}} -m(2w\mathbf {\Omega } \mathbf {r} )+\mathbf {w^{2}} \mathbf {\hat {z}} \mathbf {r} )\mathbf {\hat {z}} +m(2w\mathbf {\hat {z}} \mathbf {\Omega } +\mathbf {w^{2}} )\mathbf {r} -2m(\mathbf {\Omega } +\mathbf {\hat {z}} w)\times {\frac {d''\mathbf {r} }{dt}}}
위의 식에서 오른쪽에 있는 모든 벡터는 마지막 항을 빼고는 진자가 있는 수직면에 있다. 하지만 작은 진동에 대해
d
″
r
d
t
{\displaystyle {\frac {d''\mathbf {r} }{dt}}}
Ω
+
z
^
w
{\displaystyle \mathbf {\Omega } +\mathbf {\hat {z}} w}
z
^
(
Ω
+
z
^
w
)
=
0
{\displaystyle \mathbf {\hat {z}} (\mathbf {\Omega } +\mathbf {\hat {z}} w)=0}
w
=
−
Ω
cos
θ
{\displaystyle w=-\mathbf {\Omega } \cos \theta }
Ω
{\displaystyle \mathbf {\Omega } }
w
{\displaystyle \mathbf {w} }
θ
{\displaystyle \theta }
g
e
{\displaystyle \mathbf {g_{e}} }
w
{\displaystyle \mathbf {w} }
같이 보기 [ 편집 ] 참고 자료 [ 편집 ] Marion, B. Stephen Thornton. 『고전 동역학』. 전일동 역. 서울 : 홍릉과학출판사, 2002.
Symon. 『역학』 안동환 외 역. 서울 : 대웅출판사, 1999.
문희태. 『고전역학』. 서울 : 서울대학교출판부, 2006.