관성 모멘트 목록
(관성 모멘트의 목록에서 넘어옴)
관성 모멘트[편집]
관성 모멘트는 질량 × 길이2 의 차원을 갖는다. 다음의 목록은 한 알갱이(질점)에 대한 관성 모멘트 로부터 유도되었다.
| 설명 | 그림 | 관성 모멘트 | 비고 |
|---|---|---|---|
| 반지름이 이고 질량이 인 속이 빈 위 아래로 뚫려있는 원기둥 |  |
— | |
| 안쪽 반지름이 , 바깥 반지름이 이고 질량이 인 두꺼운 원기둥 | 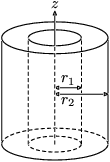
|
또는 이고 라고 하면 |
— |
| 반지름 , 높이 , 질량 인 원기둥 |  |
— | |
| 반지름 , 질량 인 얇은 원판 | 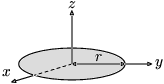 |
— | |
| 반지름 , 질량 인 구 |  |
— | |
| 반지름 , 질량 인 구 껍질 |  |
— | |
| 반지름 , 높이 , 질량 인 직원뿔 |  |
— | |
| 높이 , 너비 , 깊이 , 질량 인 직육면체 |  |
모서리 길이 , 질량 인 정육면체의 경우, . | |
| 길이 , 질량 인 막대 |  |
가느다란 선(강체)에 질량이 분포되어 있다고 가정한 근사값임. | |
| 길이 , 질량 인 막대 |  |
가느다란 선(강체)에 질량이 분포되어 있다고 가정한 근사값임. | |
| 반지름 , 단면 반지름 , 질량 인 원환체(토러스) | 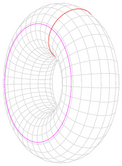 |
지름에 대해서: 수직축에 대해서: |
— |
| 꼭짓점이 , , , ..., , 질량 인 얇은 다각형 판 | 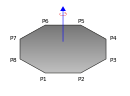 |
는 의 크기를 이야기하는 것이다. |
단면 이차 모멘트[편집]
단면 이차 모멘트는 길이4 을 차원으로 갖는다. 아래는 따로 언급하지 않으면, 도심(또는 질량중심)을 지나는 수평축에 대한 단면 이차 모멘트의 목록이다.
| 설명 | 그림 | 단면 이차 모멘트 | 비고 |
|---|---|---|---|
| 반지름 (지름 D)인 원 |  |
||
| 안쪽 반지름 , 바깥쪽 반지름 인 가운데가 빈 원 |  |
||
| 단면의 도심과 원의 중심을 지나는 수평축에 대해 각도 (라디안), 반지름 인 원호 |  |
||
| 반지름 인 반원 |  |
단면의 도심을 지나는 축에 대한 값. | |
| 반지름 인 반원 |  |
단면의 밑변을 지나는 축에 대한 값. 평행축 정리에 의해 구할 수 있음(도심으로부터 축까지의 거리는 ). | |
| 반지름 인 반원 |  |
단면의 도심을 지나는 수직축에 대한 값. | |
| 반지름 이고 1사분면에 놓여 있는 사분원 |  |
단면의 밑변을 지나는 축에 대한 값. | |
| 반지름 이고 1사분면에 놓여 있는 사분원 |  |
단면의 도심을 지나는 수평 또는 수직축에 대한 값. 평행축 정리에 의해 구할 수 있음(도심으로부터 축까지의 거리는 ). | |
| x 반지름 , y 반지름 인 타원 |  | ||
| 너비 , 높이 인 직사각형 |  |
||
| 너비 , 높이 인 직사각형 |  |
단면의 밑변을 지나는 축에 대한 값. | |
| 밑변 , 높이 인 삼각형 |  |
||
| 밑변 , 높이 인 삼각형 |  |
단면의 밑변을 지나는 축에 대한 값. 평행축 정리를 이용해 구할 수 있음(도심으로부터 축까지의 거리 ). | |
| 한 변의 길이가 인 육각형 |  |
단면의 도심을 지나는 임의의 수직축, 수평축에 대해서 동일하다. |
참고 문헌[편집]
- 전찬기, 이종헌, 정환호, 김운학, 김경진 (2015). 《토목기사 과년도 시리즈 응용역학》. 성안당. 84-85쪽. ISBN 978-89-315-6807-3.








![{\displaystyle I_{x}=I_{y}={\frac {1}{12}}m[3({r_{2}}^{2}-{r_{1}}^{2})+h^{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b3e76b71bc2bb0950003db3631128a7b3730c7e)




















































