온도
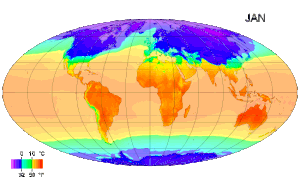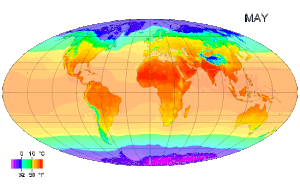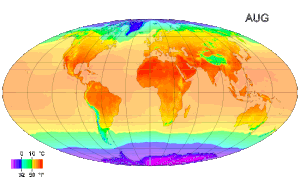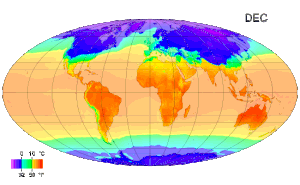

온도(溫度, 라틴어·스페인어·포르투갈어: temperatura, 독일어: Temperatur, 영어·프랑스어: temperature)는 물질의 뜨겁고 찬 정도를 나타내는 물리량이다. 온도는 물리학에서[1] 가장 기초적이고 중요한 물리량 중 하나이다. 온도는 일반적으로 다음 두 가지 방법으로 정의된다.
일반적인 정의의 온도는 온도의 경험적인 개념과, 독립적인 온도의 존재성을 보장하는 열역학 법칙중 제 0법칙에 기초한다. 일반적인 정의의 온도는 일정한 기준을 통해 만들어진 온도계로 측정되는 값이다.
열역학적 정의의 온도는 19세기 중반 열기관과 열역학에서 이어지는 통계역학이 발전되면서 에너지와 엔트로피간의 이해가 높아지면서 파생되어 나왔다. 열역학적 정의의 온도는 에너지를 엔트로피로 편미분한 값으로 나타내지며, 다양한 기초적인 물리법칙과 근본적으로 관련되어있다. 열역학적 정의의 온도는 계의 평형이 이뤄지지 않으면 정의할 수 없다.
온도의 국제 단위는 켈빈(K)이다. 켈빈은 물의 삼중점의 열역학적 온도의 1/273.16으로 정의된다. 일반적인 정의에 사용되는 온도 기준에 열역학적 정의의 온도를 사용함으로써 일반적인 정의의 온도라도 물리학적인 의미, 다양한 기초적인 물리법칙과의 관련성을 만들 수 있다.
정의[편집]
온도의 개념[편집]
온도의 개념은 우리의 경험에 비롯한 뜨겁고 차가움의 정도이다.[2]:4 우리는 경험적으로 뜨거운 물체와 차가운 물체를 접촉시키게 되면 뜨거운 물체로부터 차가운 물체로 자발적으로 에너지가 열의 형태로 흐르는 것을 알 수 있다. 따라서 온도의 개념은 "자발적으로 에너지를 밖으로 배출하려고 하는 성질의 정도"이며, 편의 상 온도가 높을수록 에너지를 많이 방출하려고 하는 성질이 크다고 정의한다.
온도의 일반적인 정의[편집]

열역학 제 0법칙은 "어떤 계 A와 B가 열적 평형상태에 있고, B와 C가 열적 평형상태에 있으면, A와 C도 열평형상태에 있다."이다. 이는 앞서 말한 온도의 개념을 생각해본다면 온도, 즉 "자발적으로 에너지를 밖으로 배출하려고 하는 성질의 정도"가 외부에 접촉한 계와 상관없이 독립적인 물리량으로 존재함을 알 수 있다. 따라서, 우리는 기준이 되는 계 몇 개를 정하고 다른 계들을 그 계와 접촉시켜 열이 흐르는 방향을 봄으로써 계의 온도의 상대적인 높낮음을 알 수 있다. 이러한 상대적인 높낮음을 절대 온도( K)나 섭씨 온도( °C)와 같이 기준을 만들어 정한다면 어떠한 계의 온도는 그 기준 내에서 이론적으로 정의가 된다. 온도의 기준과 온도에 따른 부가적인 성질들(알코올의 부피증가, 흑체복사 등)을 통해서 온도계를 만들 수 있고, 온도의 일반적인 정의는 "정해진 온도의 기준에 의하여 만들어진 온도계에서 측정되는 값"이라고 할 수 있다.[2]:5
온도의 일반적인 정의가 갖는 성질[편집]
온도의 일반적인 정의는 그 자체로 다음을 보장한다.
첫째, 온도가 다른 물체를 열 교환이 일어날 수 있도록 접촉시켰을 때 온도가 높은 물체에서 낮은 물체로 자발적으로 열이 흐르게 된다.
둘째, 두 물체가 충분한 열 교환을 통해서 열 평형에 이르렀을 때 두 물체의 온도는 같게 된다.
온도의 일반적인 정의의 문제점[편집]
온도의 일반적인 정의는 다음과 같은 개념에서 애매모호함이 있다.
첫째, 온도의 일반적 정의는 절대적 물리량으로서의 온도의 존재성을 보장하는 열역학 제 0법칙 "어떤 계 A와 B가 열적 평형상태에 있고, B와 C가 열적 평형상태에 있으면, A와 C도 열평형상태에 있다."을 근본적으로 설명하지 못한다. 즉, 일반적인 정의의 온도는 열역학 제 0법칙에 기초해야한다. (반면 뒤에 열역학적 정의는 열역학 제 0법칙과 아무런 관련이 없으며, 열역학적 정의는 오히려 열역학 제 0법칙을 증명할 수 있다)
둘째, 일반적인 온도를 정의함에 있어서 온도의 상대적인 높낮음을 통해서 온도의 기준을 정의하였는데, 그 기준에 물리적인 의미를 부여할 수 없다. 즉 일반적인 온도의 온도기준은 온도의 상대적인 높낮음에 순서를 나타낼 뿐 물리적인 의미를 가지지 않는다.
온도의 열역학적 정의[편집]
내부적으로 열 평형 상태에 이른 물리적 계의 열역학적 온도는 다음과 같이 정의된다.[2]:88
또는
열역학적 정의의 일반적인 정의의 관계[편집]
온도의 열역학적 정의는 일반적인 정의가 보장하는 다음과 같은 사실들을 잘 보장한다.
- 온도가 다른 물체를 열 교환이 일어날 수 있도록 접촉시켰을 때 온도가 높은 물체에서 낮은 물체로 자발적으로 열이 흐르게 된다.
- 두 물체가 충분한 열 교환을 통해서 열 평형에 이르렀을 때 두 물체의 온도는 같게 된다.
내부적으로 열 평형 상태에 있는 두 계 A,B가 접촉되어있어 열 교환이 자유롭게 일어난다고 하자. 열역학 제 2 법칙에 따르면 시간이 흐름에 따라 두 계의 엔트로피의 합이 증가하는 방향으로 열이 이동하며 열 평형상태에 도달하였을 때 전체 엔트로피는 최댓값에 도달한다. 각 계가 가지고 있는 에너지를 Ua, Ub라고 하자. 계 B로부터 계 A로 미소 에너지 흐름 dQ이 발생하였다고 할 때 dUa와 dUb, dStotal은 다음과 같다.
두 계가 열 평형을 이루고 있을 때 총 엔트로피는 최댓값을 가지므로 미소 dQ에 대하여 dStotal가 0이어야 한다.
, 평형상태에서
따라서,
위 식은 두 계가 열 평형에 있을 때 두 계의 온도는 같다는 것을 의미한다.
온도의 일반적인 정의와 열역학적 정의가 둘 다 필요한 이유[편집]
정해진 온도 기준에 기반하는 일반적인 온도의 정의는 19세기 중반 열역학이 발전하여 온도와 열, 엔트로피에 대한 이해가 되기 전까지 확립이 되었다. 이때의 온도의 기준은 보통 열용량, 부피팽창, 흑체복사 등에 기초하여 왜 그런지는 알지 못하지만 관계가 있는 물리량들에 기초하여 선형적으로 정의를 하였다. 반면 열역학이 발전하면서 열역학적 정의의 온도는 일반적인 온도의 정의와 다르게 그 자체로 기초적인 물리법칙과 물리량에 연관이 되어 물리적으로 큰 의미를 지니게 되었다. 열역학적 정의의 온도는 일반적인 온도의 정의와 다르게 그 자체로 물리적으로 큰 의미를 지니게 되지만, 이론에 기초하여 정의가 되므로 실제로 정확하게 측정하기에는 무리가 있다. 또한, 일반적인 온도를 정의할 때 사용되는 온도 기준을 열역학적 정의의 온도에서 따온다면 그렇게 정의된 일반적인 정의의 온도는 열역학적 정의의 온도와 같이 물리적인 의미를 가지게 된다. 이는 우리가 일반적인 정의의 온도와 열역학적 정의의 온도의 상호적인 필요성을 부각시킨다.[3]
온도의 역사[편집]
고대의 온도 정의[편집]
BC 485년 파르메니데스(Parmenides)는 그의 논문 〈자연에 관하여〉에서 프리멈 프리지덤(primum frigidum)이라는 가상의 물질을 만들어 이것이 세상의 모든 냉각을 가져온다고 주장했다. 파르메니데스의 논문을 온도에 공식적으로는 최초로 접근한 것이라 할 수 있다.
18세기의 온도 정의[편집]
1702-1703년 길리암 아몬톤(Guillaume Amontons)은 외삽법을 통해 기압이 0이 될 때는 열이 없을 것이라 생각하고 이 때의 온도를 0으로 한 아몬톤 온도를 만들어 절대 온도의 개념을 만들고자 한다. 실제로 그가 만든 아몬톤 온도에서의 절대 0도는 지금의 섭씨 온도로 환산하면 -240 °C 정도로 현재의 절대 온도로 쓰이는 -273.15 °C와도 33.15 °C의 차이만을 보인다.
온도를 정의하기 위해서 과거의 과학자들은 고정점(Fixed point)의 필요성을 느꼈다. 고정점(Fixed point)이란 온도의 기준점이 될 수 있도록 항상 같은 온도에서 관찰할 수 있는 현상을 말한다. 고정점에 따라서 온도의 기준이 달라지므로 고정점에 따라서 온도의 정의도 달라졌다. 각자의 고정점과 방법으로 온도를 정의하려 한 과학자들을 살펴보자.
| 인물 | 연도 | 제시한 고정점 |
|---|---|---|
| 산크토리우스(Sanctorius) | 1600 | 촛불의 불꽃과 눈 |
| 아카데미아 델 시멘토(Accademia del Cimento) | 1640 | 가장 추운 겨울의 추위와 가장 더운 여름의 더위 |
| 오토 본 게리크(Otto Von Guericke) | 1660 | 첫 서리 |
| 로버트 후크(Robert Hooke) | 1663 | 증류수의 냉각 |
| 로버트 보일(Robert Boyle) | 1665 | 증류수의 냉각 |
| 크리스티안 하위헌스(Christiaan Huygens) | 1665 | 물의 응고와 기화 |
| 호노르 파브리(Honore Fabri) | 1669 | 눈과 최고의 여름 더위 |
| 프란세스코 에스치나르디(Francesco Eschinardi) | 1680 | 얼음의 융해와 물의 기화 |
| 호아침 달렌스(Joachim Dalence) | 1688 | 물의 응고와 버터의 융해 또는 얼음과 지하고 |
| 에드먼드 헬리(Edmond Halley) | 1693 | 깊은 동굴과 끓어오르는 알콜(spirit) |
| 카를로 레날디니(Carlo Renaldini) | 1694 | 얼음의 융해와 물의 끓음 |
| 아이작 뉴턴(Issac Newton) | 1701 | 눈의 융해와 혈액의 열 |
| 길라암 아몬톤(Guilaume Amontons) | 1702 | 끓는 물 |
| 올레 뢰머 | 1702 | 눈과 염의 혼합물과 끓는 물 |
| 필리프 데 라 이레(Phillippe de la Hire) | 1708 | 어는 물과 파리 천문대의 지하고 |
| 다니엘 파렌하이트 | 1720 | 얼음, 물, 염의 혼합물 & 얼음, 물 혼합물 & 건강한 체온 |
| 존 파울러(John Fowler) | 1727 | 어는 물과 손으로 잡을 수 있는 가장 뜨거운 물 |
| 레아무어(R.A.F. de Reamur) | 1730 | 어는 물 |
| 조제프 니콜라스 드 이슬레(Joseph-Nicola D l’Isle) | 1733 | 끓는 물 |
| 안데르스 셀시우스(Anders Celsius) | 1741 | 얼음의 융해와 끓는 물 |
| J. B. 미켈리 두 크레스트 | 1741 | 파리 천문대 지하고와 끓는 물 |
| 브리태니커 백과사전 | 1771 | 어는 물과 밀랍 |
셀시우스의 온도 단위[편집]

안데르스 셀시우스(Anders Celsius)는 최초로 국제적으로 사용될 수 있는 표준 온도 단위를 만들고자 시도했다. 그는 그의 논문 〈온도계의 두 고정된 온도에 대한 관찰〉(Observations of two persistent degrees on a thermometer)에서 물의 어는점은 기압에 무관하지만 끓는점은 기압에 의존한다는 실험 관찰 결과를 밝힌다. 현대의 측정 결과와 비교해봐도 손색없을 정도로 그의 측정은 정확했으며 표준 기압에서 벗어나는 압력에 의한 온도 변화를 보정할 수 있는 방법도 고안하여 온도의 단위를 제시했다. 그는 그의 온도를 스웨덴의 웁슬라 왕립과학학회(Royal Society of Sciences in Uppsala)에 제안하여 물의 끓는점을 0 °C로, 어는 점을 100 °C로 정의했다. 하지만 이후 1745년에 칼 리네우스(Carolus Linnaeus)에 의해 편의상 물의 어는점이 0 °C로, 끓는 점이 100 °C로 바뀌어 정의된다.
요한 람베르트의 온도계[편집]
1777년 요한 람베르트(Johann Heinrich Lambert)는 그의 저서 《피로메트리에》(Pyrometrie)에서 일정한 부피를 가진 기체에서의 압력과 온도의 관계를 이용한 절대 온도계를 만들었다. 이 온도계를 이용해 람베르트는 기체의 압력이 0에 다다랐을 때의 온도를 절대 영도로 정의하고 외삽법을 통해 절대영도를 -270 °C라는 현대의 값과 매우 가까운 값을 얻어낸다.
파렌하이트의 온도 단위[편집]

1724년 다니엘 가브리엘 파렌하이트는 세 가지 고정점을 이용했다. 가장 먼저 얼음, 물, 염화암모늄으로 이루어진 혼합물이 평형을 이뤘을 때의 온도를 0 °F로 정의했다. 물의 어는 점을 두 번째 고정점, 32 °F로 이용했고 마지막으로 세 번째 고정점, 96 °F는 사람의 체온으로 정의했다. 이후에 파렌하이트는 자신의 온도를 이용하면 600도 부근에서 수은의 끓는점이 나타난다는 사실을 알아냈다. 그리고 물은 어는점보다 약 180도 높은 온도에서 끓는다는 사실을 알아냈다. 하지만 파렌하이트가 정의했던 온도에서는 물의 끓는점이 32도보다 약 180도보다 높은, 애매모호한 온도에서 나타났기 때문에 훗날에는 물의 끓는점이 212 °F가 되도록 화씨 온도가 새롭게 정의됐다.
고정점의 안정성에 대한 논란[편집]
이렇게 고정점을 기준으로 온도를 정의했기 때문에 기준으로 삼은 자연 현상이나 상태는 확실하게 고정되어 있어야 한다는 문제가 있었다.[4]
런던 왕립학회의 토의[편집]
1776년 런던 왕립학회에서는 온도를 정의하는데 필요한 고정점들에 대한 제안받기 위한 위원회를 구성한다. 물이 끓는 현상을 고정점으로 하는 과학자들이 당시에도 많았는데 물의 끓음 현상은 여러 문제점을 안고 있었다. 먼저, 물의 끓음 현상은 기압에 의존했기 때문에 기압에 대해서는 고정이 되지 안 됐다. 이를 해결하기 위해서 왕립학회의 위원회에서 제안된 것은 29.8inHg(=756.9mmHg=0.996atm)의 기압을 기준으로 하자는 것이었다. 두 번째 문제점은 온도계 내부의 열 전달 문제였다. 당시에는 수은온도계가 사용됐었는데 온도계의 구부에 있는 수은의 온도와 온도계의 수은기둥의 수은의 온도가 다르기 때문에 정확히 측정하고자 하는 온도가 측정되지 않았다. 이를 해결하기 위해서 런던 왕립학회는 온도계를 구부는 물론이고 온도계 전체를 물에 담그면 된다는 해결책을 내놓았다.
데루크의 이의 제기[편집]

하지만 가장 심각한 문제점은 물이 정확히 고정된 온도에서 끓는 것이 아니라 끓으면서 온도변화를 한다는 것이었다. 온도에 따라서 그 끓음의 정도도 다르게 나타났다. 스위스의 지질학자이자 기상학자였던 제안 안드레 데루크(Jean-Andre Deluc)는 “물이 끓기 시작할 때, 물이 가질 수 있는 최대의 열을 가지고 끓지 않는다. 그러기 위해서는 물 전체, 즉 용기의 바닥부터 물의 표면까지 가장 격렬한 상태로 끓어야 한다. 물이 끓기 시작할 때부터 가장 격렬하게 끓는 상태까지 물의 온도는 1도 이상의 열을 흡수한다”고 얘기했다. 데루크(Jean-Andre Deluc)를 비롯하여 조제프 루이 게이뤼삭, 프랑코이 마르셋(Francois Marcet), 프랑코이 마리에 루이(Francois Marie Louis), 루이 듀포어(Louis Dufour), 조지 크렙스(Georg Krebs)가 물의 끓음 현상과 온도의 관계를 탐구했다. 이들 모두 일반적으로 정의된 끓는점은 물이 정확하게 끓게 하는 온도가 아니라는 것에는 동의했지만 실제로 어떤 상태로 물이 끓는지에 관해서는 모두 다른 의견을 가지고 있었다.[4] 하지만 그럼에도 불구하고 물의 끓음 현상은 이후에도 고정점으로서의 의미를 유지하게 되는데 이는 끓는 점을 초과하는 온도에서도 완전한 끓음이 시작되면 온도가 떨어지기 때문이다. 또 끓는 점을 초과하는 온도에서 끓는 현상은 가장 자연스러운 상태에서 물을 끓임으로써 해결할 수 있었다.[4]
물의 끓음 현상을 고정점으로 사용하면서 끓음 현상의 차이를 극복할 수 있는 방법으로는 끓어서 생긴 수증기의 온도를 재는 방법이 제시되었다. 1777년 헨리 캐번디시는 “끓는점을 보정할 수 있는 가장 정확한 방법은, 온도계를 물에 넣는 것이 아니라 닫혀 있는 용기의 수증기에 노출시키는 것이다.”라고 했으나 같은 해에 이에 대해 데루크(Jean-Andre Deluc)은 “이론적인 것을 떠나, 수증기와 물은 수증기가 생성되기 전에 섞여 있기 때문에 서로의 온도에 영향을 미치기 때문에 수증기의 온도를 측정하는 것이나 물의 온도를 측정하는 것이나 그 문제점은 그대로 드러난다”라고 반박했다. 하지만 1842년에 프랑코이 마르셋(Francois Marcet)은 물은 105 °C에서도 끓지만 증기의 온도는 이 때 1 °C범위 내에서 초과한다는 실험을 통해 증기의 온도를 재는 방법이 해결책이 될 수 있음을 확인한다. 이후로 게뤼사크를 비롯하여 프랑코이 마르셋(Francois Marcet), 루이 듀포어(Louis Dufour), 마셸 에밀레 베르뎃(Marchel Emile Verdet), 데시르 게르네즈(Desire Gernez), 샤를 톰린슨(Charles Tomlinson) 등의 사람들의 다양한 방법으로 온도와 물의 끓음에 대한 연구를 계속했다. 1880~1881년에 존 에이켄(John Aitken)은 수증기의 온도는 물의 끓는 온도만큼이나 불안정하게 고정되어 있다고 주장했다. 존 에이켄(John Aitken)에 따르면 증기의 온도가 안정된 고정점처럼 보였던 이유는 공기 중의 먼지 때문이었고 먼지가 걸러지면 물의 끓는점을 측정하는 것과 마찬가지라는 것을 보였다.[5]
이후 데루크(Jean-Andre Deluc)의 제안대로 의해 온도를 수은온도계로 재는 것을 정의로 하는 방향으로 흘러간다.
19세기의 온도 정의[편집]
열소론적 정의[편집]
이후에는 온도를 열소론으로 정의하려는 윌리엄 어바인(William Irvine), 레느 저스트 하위(René Just Haüy), 피에르시몽 라플라스(Pierre-Simon Laplace) 등이 등장했다.
윌리엄 어바인(William Irvine)은 열소(caloric)이라는 물질이 열의 원인 또는 열 그 자체라고 주장했다. 그의 이론에 따르면 열소의 양은 열용량과 절대온도의 곱으로 나타낼 수 있으며 따라서 열용량은 물체가 열소를 저장할 수 있는 용량으로 정의했고 절대온도는 열소의 정량적인 값으로 정의했다. 잠열은 열용량이 변할 때 일정한 온도를 유지하기 위해 필요한 열로 정의했다.
이후 1808년 존 돌턴은 뜨거운 물과 차가운 물을 섞을 때 부피의 합보다 합쳐진 부피가 작기 때문에 열용량이 작아져 열소의 양을 유지하기 위해 온도가 상승하게 된다는 이론을 내놓았다.

이후 앙투안 라부아지에(Antoine Lavoisier)는 결합 열소(combined caloric)를 물질과 화학적으로 결합된 열소로 온도에 영향을 주지 않는 열소로 분류했고 자유 열소(free caloric)를 물질과 결합되지 않은 열소로 온도에 영향을 주는 열소로 분류했다.
레느 저스트 하위(René Just Haüy)는 1803년 《자연철학에 관한 논문》(Elementary Treatise on Natural Philosophy)에서 물체가 열을 받아 팽창할 때 부피 팽창은 결합 열소 때문이고 온도 상승은 자유 열소 때문이라고 주장했다. 또, 낮은 온도에서는 분자간 거리가 작아 더 큰 인력이 필요하므로 결합 열소가 더 많이 결합되어야 한다.

1821년에는 피에르시몽 라플라스(Pierre-Simon Laplace)는 결합 열소를 분자에 결합된 열소로 척력이 작용하지 않는 열소로 재정의했고 자유 열소는 분자에 결합된 열소로 척력이 작용하는 열소로 정의했다. 공간의 자유 열소는 물질에 결합하지 않은 열소이고 최종적으로 온도는 공간에 존재하는 자유 열소의 밀도로 정의했다.
분자 운동론적 정의[편집]
온도에 대한 역학적 이론들이 등장을 하는데 이 이론들은 열을 입자들의 움직임으로 해석했다. 벤저민 톰프슨(Benjamin Thompson)은 분자들은 고정점들에 대해 진동을 하고 있고 온도는 이 진동의 진동수로 볼 수 있다고 주장했다. 또, 진동하는 분자들은 에너지 손실이 없고 그렇기 때문에 절대적으로 0°가 되는 온도도 없다고 주장했다. 존 헤라패스(John Herapath)는 온도가 분자의 속도에 비례한다고 주장했지만 존 와터슨(John Waterston)은 온도가 분자의 에 비례한다고 주장했다.
샤를의 법칙과 게이뤼삭의 절대 영도[편집]

1802년 자크 알렉상드르 세사르 샤를은 일정한 압력에서 온도에 따른 기체의 부피 변화를 연구한다. 그는 그의 발견을 출판하지 않았지만 기체의 온도와 부피가 선형적으로 비례한다는 샤를의 법칙을 발견한다.
조제프 루이 게이뤼삭은 실험 자료를 바탕으로 절대 영도가 -273 °C에 있을 것이라 예측했고 기체 팽창 계수에 대해 처음으로 273이라는 수를 쓰기 시작했다.
카르노의 열기관 고안[편집]

1824년에 사디 카르노는 고온에서 저온으로 열이 흐르면서 일을 할 수 있는 열기관을 고안해낸다. 이 열기관은 카르노 순환을 따르는데 카르노 순환이란 과정 1에서 기체가 고온 A에서 열을 받아 등온 과정을 거쳐 팽창하며 과정 2에서는 A를 제거하고 단열 과정을 거쳐 팽창한다. 그 다음 과정 3에서는 저온 B에 열을 내보내며 다시 등온 과정을 거치며 수축한다. 마지막으로 과정 4에서는 B를 제거한 후 단열 과정으로 수축시켜 다시 초기 상태로 되돌리고 이 순환과정을 카르노 순환이라고 한다. 그리고 이 카르노 순환을 따르는 열기관의 효율은 고온의 온도와 저온의 온도에만 의존한다는 것을 보인다.
톰슨의 절대 온도[편집]
앞선 아몬톤의 시도, 카르노와 클레이페론의 이론에 영향을 받아 1848년에 윌리엄 톰슨은 절대온도를 물질에 관계없이 1도를 카르노 순환에서 단위일을 하는데 필요한 열의 양으로 정의한다. 이 때 제임스 줄은 열과 일이 상호변환 가능하며 그렇기 때문에 열기관에서 고온에서 열기관으로 흘러들어온 열은 일부 일로 변환되고 남은 열이 저온으로 흘러나간다고 주장했다. 그리고 1854년에 톰슨은 이를 받아들여 카르노의 이론을 재정립하고 절대 온도에 대한 두 번째 이론을 만들어낸다.
윌리엄 톰슨은 그의 논문 〈온도의 단위에 대하여〉(On the Thermometric Scale)에서 절대 영도의 정의와 그를 기준으로 한 온도 단위의 필요성을 주장한다. 그는 자크 알렉상드르 세사르 샤를과 조제프 루이 게이뤼삭의 앞선 연구에서 얻어낸 온도에 따른 기체의 팽창 계수 0.00366의 역수에 음의 값을 취한 -273.22 °C를 절대 영도로 정의하고 섭씨 온도의 눈금 크기를 사용하는 새로운 온도의 단위를 만들고 이를 켈빈이라 정의했다.
랭킨의 온도 단위[편집]
윌리엄 랭킨(William John Macquorn Rankine)은 윌리엄 톰슨의 온도 단위와 거의 같은 온도를 정의했으나 그는 섭씨 온도의 눈금 크기를 사용하는 대신 화씨 온도의 눈금 크기를 사용했다.
현대 온도 정의의 확립[편집]
1930년대의 단위 조정[편집]
1930년대에 기체의 온도에 따른 부피 팽창 실험을 정밀하게 한 결과 물의 어는점을 0 °C라 했을 때 절대 영도는 -273.15 °C로 나타났다.
국제 도량형 총회의 온도 확립[편집]
1948년 제 9회 국제 도량형 총회(CGPM: Conférence Générale des Poids et Mesures, General Conference on Weights and Measures)의 세 번째 안건에 따르면 물의 삼중점을 정확히 0.1 °C로 약속했다. 그리고 이후 1954년 제 10회 국제 도량형 총회의 세 번째 안건에 따르면 캘빈 온도의 눈금 크기를 확립하기 위해서 물의 삼중점(0.01 °C)을 273.16K으로 약속했다. 즉, 물의 어는점과 삼중점의 온도차를 0.1K으로 약속한 것이다. 1967-1968년 제 13회 국제 도량형 총회의 네 번째 안건에서는 캘빈 온도의 눈금 크기를 물의 삼중점의 으로 정의했다. 그리고 마지막으로 국제 도량형 위원회(CIPM: Comité international des poids et mesures, International Committee for Weights and Measures)는 엄밀한 정의를 위해 비엔나의 표준 물(Vienna Standard Mean Ocean Water)과 같은 성분을 가진 물의 삼중점을 273.16K으로 정의했다.
온도와 운동, 에너지간의 관계[편집]
병진운동과 운동에너지[편집]

충분히 큰 계(통계역학적으로 충분한 입자 수를 갖추고 있는)의 열역학적 온도는 입자들의 병진운동 속도의 평균 평방근에 비례한다. 입자의 병진운동은 x,y,z 총 세 개의 자유도를 통해 움직인다. 이 특정한 형태의 운동에너지를 역학적 온도라고도 정의한다. 병진운동은 열역학적 온도뿐만 아니라 압력과 부피에도 관계를 가지는데, 특히 이상기체에서 이상기체 상태방정식 를 유도해 낼 수 있다.[2]:238~240 병진 운동에너지 뿐만이 아니라 진동운동이나 회전운동과 같이 에너지가 미시상태를 나타내는 변수의 제곱에 비례하는 자유도일 경우 그 자유도가 가지는 한 입자의 평균 에너지는 다음과 같이 온도와 볼츠만 상수의 곱의 절반으로 정해지게 된다.
이는 에너지 등분배법칙 :
- “이차식 형태 에너지의 한 자유도에 대한 평균 에너지는 이다.”
으로, 고전적 통계역학의 가장 중요한 결과중 하나이다. 이는 온도와 계의 운동에너지의 상관관계를 의미한다.[2]:238~240
흑체복사[편집]

온도를 가진 물체가 다른 온도를 가진 물체와 열 교환을 하는 방식에는 전도, 대류, 복사 이렇게 크게 세 가지가 있다. 전도는 열적으로 접촉하고 있는 두 계의 분자들이 직접 충돌하여 에너지를 교환하는 방식이고, 대류는 온도가 다른 두 계에서 분자들이 직접 움직이며 섞임으로써 에너지를 교환하는 방식이다. 복사는 분자들이 가진 온도에 의해 방출되는 빛을 통해 에너지를 교환하는 방식인데, 이상적인 흑체의 경우에는 진동수 혹은 파장에 따른 빛의 세기는 플랑크 법칙을 따른다.
온도가 T인 흑체에서 방출되는 복사에서 진동수가 ν이고 파장이 λ인 빛의 세기는 다음과 같다.
온도의 과학에서의 쓰임[편집]
온도는 물리학 외의 다른 과학 분야에서도 많이 쓰이는 물리량이다. 그 중 대표적인 것은 화학에서의 반응속도, 생물학에서의 효소의 활성온도, 천문학에서의 천체의 표면온도 등이 있다.
화학[편집]
아래는 화학에 대한 내용이다.[6]
반응의 자발성[편집]
화학반응의 자발성은 기브스 자유 에너지에 의해 결정되는데, 그 식은 아래와 같다.
따라서 온도에 따른 엔탈피 변화량과 엔트로피 변화량이 주어져 있다면 어떤 특정 온도에서 그 반응의 자발성을 예측할 수 있는데, 이면 정반응이 자발적으로 일어나고, 이면 역반응이 자발적으로 일어난다. 이면 반응은 평형 상태에 있게 된다.
반응속도[편집]
위와 같은 화학반응에서 반응속도는 아래와 같다.
여기에서 [A]는 A의 몰 농도, [B]는 B의 몰 농도이고, k는 반응속도상수라고 한다. 반응속도상수는 온도에 의존하는 값인데, 아레니우스 방정식에 의해 결정된다.
은 기체 상수, 는 반응이 일어날 때의 절대온도, 는 반응의 활성화 에너지, 그리고 는 빈도계수 또는 빈도인자라고 한다. 따라서 온도가 증가할수록 반응속도상수가 증가한다.
생물[편집]
효소[편집]
효소는 생명체 내부에서 일어나는 화학 반응을 매개하는 단백질 촉매이다. 촉매 작용을 하는 원리는 기질과 결합하여 촉매-기질 복합체를 형성함으로써 화학 반응의 활성화 에너지를 낮추어 반응속도를 빠르게 하는 것이다. 하지만 효소는 단백질로 이루어져 있으므로 온도가 변하면 단백질이 변형되어 기질과 잘 결합하지 못하게 될 수 있다. 따라서 효소의 활성도는 온도에 의존한다.
인체 내부에 있는 아밀라아제는 α-아밀라아제인데, 최적온도는 체온 부근이다. 반면에 β-아밀라아제의 경우에는 박테리아, 곰팡이, 그리고 여러 식물들에 존재하는 효소인데, 최적온도는 약 섭씨 60도 부근이다. 이처럼 같은 효소라 할 지라도 구조가 다르면 최적온도가 다를 수 있다.
천문학[편집]
천문학에서 온도는 천체를 종류별로 분류하는 데에 쓰이거나 우주 공간에 존재하는 복사의 종류를 나타낼 때 쓰인다. 천체들은 모두 흑체로 가정하며, 천체를 온도별로 분류하는 방법은 하버드 스펙트럼 분류법이 있다. 주로 쓰이는 온도의 종류에는 아래와 같이 네 가지가 있다.[7]
유효온도[편집]
별에서 방출되는 플럭스를 전 파장에 걸쳐 합친 플럭스, 즉 관측된 전체 플럭스와 동일한 양의 플럭스를 방출하는 흑체의 온도를 유효온도라고 한다.
따라서 유효온도는 아래와 같이 된다.
색온도[편집]
두 파장 대에서 관측된 복사 세기의 비와 동일한 비의 복사를 방출하는 흑체의 온도를 색온도라 한다.
위의 식은 플랑크 법칙에 따른 것이며 식을 따르는 가 바로 천체의 색온도가 된다.
밝기온도[편집]
밝기온도는 관측된 표면 밝기와 동일한 밝기를 가지는 흑체의 온도이다.
위 식을 만족하는 가 바로 천체의 밝기온도이며, 우변은 플랑크 법칙을 통해 계산할 수 있다.
운동온도[편집]
일정한 온도를 가지는 분자들은 열운동을 한다. 그 열운동에 의해 생기는 속도 때문에 분자들 사이에 속도 차이가 생기게 되고, 도플러 효과가 생기는데 이 효과를 열적 도플러 확장이라 한다. 열적 도플러 확장에서 파장 변화는 다음과 같은 식에 의해 계산될 수 있다.
이렇게 해서 계산된 분자들의 열운동에 의한 속도 차이는 분자들의 평균 속력 또는 평균 평방근(root mean square) 속력의 두 배가 된다. 그 속도 차이가 평균 평방근 속력의 두 배라고 가정한다면 기체 분자의 운동에너지 식에 따라 운동온도는 아래와 같이 된다.
온도의 예[편집]
| 온도 | 흑체복사시 최대의 에너지를 가지는 파장[8] | ||
|---|---|---|---|
| K | °C | ||
| 절대온도 | 0 K | −273.15 °C | 정의될 수 없음 |
| 인간이 도달한 최저 온도[9] | 100 pK | −273.149999999900 °C | 29,000 km |
| 가장 차가운 보스 아인슈타인 응축(Bose-Einstein condensation)[10] | 450 pK | −273.14999999955 °C | 6,400 |
| 1 mK | 0.001 K | −273.149 °C | 2.89777 m (radio, FM band)[11] |
| 물의 삼중점 | 273.16 K | 0.01 °C | 10,608.3 nm (long wavelength I.R.) |
| 물의 끓는점 | 373.1339 K | 99.9839 °C | 7,766.03 nm (mid wavelength I.R.) |
| 백열전구 | 2500 K | ≈2,200 °C | 1,160 nm (near infrared) |
| 태양의 표면 | 5,778 K | 5,505 °C | 501.5 nm (green-blue light) |
| 번개 | 28 kK | 28,000 °C | 100 nm (far ultraviolet light) |
| 태양의 핵 | 16 MK | 16 million °C | 0.18 nm (X-rays) |
| 열핵폭탄[12] | 350 MK | 350 million °C | 8.3×10−3 nm (gamma rays) |
| 거대한 별의 폭발 전 핵[13] | 3 GK | 3 billion °C | 1×10−3 nm (gamma rays) |
| 대형중이온충돌기[14] | 1 TK | 1 trillion °C | 3×10−6 nm (gamma rays) |
| CERN의 양성자 vs 핵 충돌[15] | 10 TK | 10 trillion °C | 3×10−7 nm (gamma rays) |
| 빅뱅 후 5.391×10−44 s 뒤의 우주 | 1.417×1032 K (Planck tempearature) |
1.417×1032 °C | 1.616×10−26 nm (Planck Length)[16] |

측정방법[편집]
온도를 측정하는 기구를 온도계라고 부른다. 온도계를 구성하고 있는 것을 나눠보면 일반적으로 온도를 감지하는 측온부 (온도검출단)와 측온부에서 감지한 온도를 직접 또는 간접적으로 표시하는 표시부(수신계기), 측온부와 표시부를 연결시켜 주는 도선 또는 배관으로 이뤄져 있다. 뿐만 아니라 액체 글라스 온도계와 같이 측온부와 표시부가 일체형으로 된 것도 있다. 온도계는 측정 방법에 의해 측온부를 피측정 물체에 직접 접촉시켜 온도를 측정하면 접촉법, 그리고 접촉시키지 않고 측정하면 비접촉법으로 분류한다.

접촉법[편집]
열은 고온에서 저온으로 이동하고, 온도가 두개 이상의 물체에 접촉시켜 충분한 시간이 주어지면 접촉된 물체들은 온도가 같게 되는 열평형 상태를 이루게 된다. 즉, 열역학 제 0법칙에 의해, 임의 두 물체가 각각 제3의 물체와 열평형을 이룬다면 임의 두 물체도 열평형 상태에 있게 된다. 따라서 온도를 측정하고자 하는 피측정 물체에 측온부를 접촉시켜 피측정 물체와 측온부가 열평형 상태에 이르렀을 때 감온부의 변화량을 측정함으로써 피측정 물체의 온도를 감지하는 방식이다. 이 방법에 의한 온도 계에서는 감온부와 측정대상의 접촉의 정도에 따라 측정정도 크기가 좌우된다. 그래서 측온부를 측정대상에 접촉 할 수 없는 경우는 측정이 불가능하며, 접촉에 의해서 측정대상이 영향을 받게 되는 경우는 큰 오차가 생긴다. 이와 같이 접촉방식을 이용한 온도계로는 유리제온도계, 압력식온도계, 열전대, 바이메탈식 온도계, 저항식 온도계 등이 있다.
비접촉법[편집]
피측정 물체에 감온부를 직접 접촉하지 않는 상태에서 피측정 물체로부터 나오는 빛 또는 열을 감지하여 온도와 빛, 열 에너지와의 일정한 관계를 이용하여 온도를 측정하는 측정방식이다. 측정대상으로부터 방출된 에너지의 강도는 절대온도의 4승에 비례하기 때문에 1000 ℃ 이하의 온도 범위에서는 측정정도가 나쁘나, 장점으로는 움직이는 피측정 대상 및 검출하고자 하는 대상이 보이기만 하면은 쉽게 접촉하지 않고 온도를 측정할 수 있다. 비접촉 방식에 의한 온도계측에 사용되는 것으로는 방사온도계, 광고온계, 색온도계, 적외선온도계(열선) 등이 있다.
단위[편집]
온도의 단위로는 여러 가지가 있는데 현재 국제 표준화 기구(ISO) 에서는 국제단위계(International System of Unit, SI)로 켈빈(K)을 사용하고 있다. 켈빈(K)은 절대 온도를 측정하므로, 0K은 절대 영도(이상 기체의 부피가 0이 되는 온도)이다. 이뿐만 아니라 각자 측정방법에 따라 기준을 다르게 잡아 섭씨(℃), 화씨(°F) 라는 온도 단위도 있다. 섭씨온도는 1742년 스웨덴의 천문학자 안데르스 셀시우스가 처음으로 제안하였으며 이는 1atm 에서의 물의 어는점을 0℃, 끓는점을 100℃로 두고 그 사이를 100등분 하여 정한 것이다. 화씨 온도는 독일의 다니엘 가브리엘 파렌하이트의 이름을 딴 온도 단위이며, 이는 1atm에서 물이 어는 온도를 32 °F, 물이 끓는 온도를 212 °F로 두고 이 사이의 온도를 180등분 하여 정한 것이다.
섭씨, 화씨, 켈빈, 랭킨 간의 환산 관계[편집]
- 섭씨→화씨 : °F = °C × (9/5) + 32
- 섭씨→켈빈 : K = °C + 273.15
- 화씨→섭씨 : °C = (°F - 32) x (5/9)
- 화씨→켈빈 : K = (°F - 32) / 1.8 + 273.15
- 화씨→랭킨 : °R = °F + 459.2
- 켈빈→섭씨 : °C = K - 273.15
- 켈빈→화씨 : °F = (K - 273.15) × 1.8 + 32
- 켈빈→랭킨 : 1 K= 1.8 °R
음의 온도[편집]
음의 온도란 절대 영도(0K)보다 낮은 온도를 말한다. 열역학 제3법칙에 따르면 절대 0도보다 낮은 온도는 존재할 수 없다. 하지만 가능한 에너지의 상태가 제한되어 있는 전자와 핵의 스핀을 양자역학적 관점에서 봤을 때, 절대 영도보다 작은 음의 온도를 만드는 것은 충분히 가능한 일이다. 다만 이것은 거시적 관점에서의 온도에는 해당되지 않고, 에너지 등분배의 법칙에 따라 에너지를 서로 교환하거나 하지 않는 고립된 특별한 자유도에 대해서만 해당하는 것이다. 음의 온도는 바닥 상태에 있는 스핀들에 대해서 밀도 반전 (population inversion) 을 일으키는 “Radio Frequency Technique”[17][18]를 통해서 실험적으로 만들어질 수 있다. 높은 에너지 준위를 가지는 상태의 수가 많아지면 계 전체의 에너지가 증가하고, 계의 무질서도가 증가하면서 엔트로피 또한 증가하게 된다. 결국 계 전체의 에너지가 일정 값이 되면 높은 에너지 준위를 가지는 상태의 수와 낮은 에너지 준위를 가지는 상태의 수가 같게 되어 엔트로피가 최대가 되고, 높은 에너지 준위를 갖는 상태의 수가 많아짐에 따라 계 전체의 에너지가 증가하면 계의 상태가 정돈되고, 엔트로피가 다시 낮아지게 된다. 따라서 계의 총 에너지와 엔트로피에 대한 그래프는 위로 볼록한 함수의 꼴을 띠게 된다. 여기에서 온도의 열역학적 정의에 따라 이고, 극대점에서 그래프의 기울기는 0이므로 극대점에서 온도는 특이점(singularity)이 된다. 또한 극대점 이후에서는 그래프의 기울기는 음이므로 이 부분에서는 음의 온도가 생긴다. 계의 에너지가 계속 커지면 음의 온도는 0에 수렴하게 된다. 밀도 반전 상태에서 생기는 음의 온도는 에너지가 높은 상태이므로 양의 온도보다 오히려 더 뜨거운 상태이며, 음의 온도를 가지고 있는 계와 양의 온도를 가지고 있는 계가 접촉을 하게 된다면 음의 온도를 가지고 있는 계의 에너지가 양의 온도를 가지고 있는 계로 흘러갈 것이다.
주거환경[편집]
사람이 살고 있는 주거환경은 지역의 기후와 풍토에 적응한 생활양식과 함께 개선되어왔다. 체온조절의 부담이 가장 적은 온도, 다시 말하면 덥지도 춥지도 않는 최적온도는 18℃ 정도이며, 15.6~20℃ 정도에서 쾌적함을 느낄 수 있다고 한다.
사람이 주변환경으로부터 쾌적함을 유지하려면 온도 외에도 습도를 고려해야 하는데, 습도가 30% 미만이거나 80% 이상이면 좋지 않고, 약 40~60% 정도면 대체로 쾌적함을 느낄 수 있다. 실제로 쾌적함을 주는 습도는 온도에 따라 달라지는데 15℃에서는 약60%정도, 18~20℃에서는 약50%, 21~23℃에서는 약40%, 24℃ 이상에서는 대략 35%정도에서 적당한 습도로 여겨진다.
사람이 느끼는 춥고 덥다는 감각은 겨울은 추위에 대하여, 여름은 더위에 대하여 민감하게 반응하는 편이다. 또 같은 기온이라 하더라도 봄에는 가을보다 보통 두껍게 옷을 입고 있는점을 감안하면 이와 같은 사항들이 복합되어 최적온도는 겨울에는 낮아지고 여름에는 높아지는 경향이 있다.[19]
이처럼 체온조절을 위한 온도만큼이나 습도는 면역력을 유지하고 건강한 신체활동을 하는데 있어 매우 중요하다고 할 수 있다. 한편 겨울철 실내온도에 대한 적정 온도는 18℃~20℃라고 보건복지부와 질병관리본부는 발표한바 있는데 이 역시 외부 온도와의 차이 그리고 내복이나 방한용품 착용을 활용한 체온조절 그리고 쾌적한 습도의 유지가 용이함등 현대적으로 개선되어온 과학적인 생활양식을 반영하고 있다.[20]
온도 범위[편집]
국립환경과학원은 환경시험기준에서 온도표시에 대해 다음과 같은 기준을 사용하고 있다.[21]
| 온도표시 | 온도 범위 | 비고 |
|---|---|---|
| 냉수 | 15 ℃ 이하 | |
| 상온 | 15 ℃ ∼ 25 ℃ | |
| 온수 | 60 ℃ ∼ 70 ℃ | |
| 열수 | 약100 ℃ | 끓는물 |
같이 보기[편집]
- 국제 도량형 총회
- 기온
- 기브스 자유 에너지
- 끓는점
- 대류
- 앙투안 라부아지에
- 조제프 루이 게이뤼삭
- 맥스웰의 도깨비
- 볼츠만 상수
- 사디 카르노
- 삼중점
- 색온도
- 섭씨
- 어는점
- 에너지 등분배법칙
- 에너지
- 엔탈피
- 엔트로피
- 열
- 열기관
- 열역학
- 열전도
- 온도계
- 유효온도
- 일
- 자유도
- 자크 알렉상드르 세사르 샤를
- 절대 영도
- 절대온도
- 켈빈
- 통계물리
- 피에르시몽 라플라스
- 헬름홀츠 자유 에너지
- 흑체복사
각주[편집]
- ↑ Temperature measurement and Sensor Technology (2019).
- ↑ 가 나 다 라 마 Daniel V.schroeder. 《An Introduction to thermal physics》. Addison Wiesley Longman.
- ↑ “Why do we need both thermodynamic and practical temperature scales?”. 2012년 8월 7일에 원본 문서에서 보존된 문서. 2012년 11월 17일에 확인함.
- ↑ 가 나 다 Hasok Chang. 《Inventing Temperature》. Oxford University Press.
- ↑ Hasok Chang. 《Inventing Temperature》. Oxford University Press.
- ↑ “네이버 지식백과”. 2008.
- ↑ Zeilik, Gregory (1998). 《Introductory Astronomy & Astrophysics, 4e》. BROOKS/COLE. ISBN 0-03-006228-4.
- ↑ 《The cited emission wavelengths are for black bodies in equilibrium. CODATA 2006 recommended value of 2.8977685(51)×10−3 m K used for Wien displacement law constant b.》.
- ↑ 《"World record in low temperatures". Retrieved 2009-05-05》.
- ↑ 《A temperature of 450 ±80 pK in a Bose–Einstein condensate (BEC) of sodium atoms was achieved in 2003 by researchers at MIT. Citation: Cooling Bose–Einstein Condensates Below 500 Picokelvin, A. E. Leanhardt et al., Science 301, 12 Sept. 2003, p. 1515. It's noteworthy that this record's peak emittance black-body wavelength of 6,400 kilometers is roughly the radius of Earth.》.
- ↑ 《The peak emittance wavelength of 2.89777 m is a frequency of 103.456 MHz》.
- ↑ 《The 350 MK value is the maximum peak fusion fuel temperature in a thermonuclear weapon of the Teller–Ulam configuration (commonly known as a hydrogen bomb). Peak temperatures in Gadget-style fission bomb cores (commonly known as an atomic bomb) are in the range of 50 to 100 MK. Citation: Nuclear Weapons Frequently Asked Questions, 3.2.5 Matter At High Temperatures. Link to relevant Web page. All referenced data was compiled from publicly available sources.》.
- ↑ 《Core temperature of a high–mass (>8–11 solar masses) star after it leaves the main sequence on the Hertzsprung–Russell diagram and begins the alpha process (which lasts one day) of fusing silicon–28 into heavier elements in the following steps: sulfur–32 → argon–36 → calcium–40 → titanium–44 → chromium–48 → iron–52 → nickel–56. Within minutes of finishing the sequence, the star explodes as a Type II supernova.》.
- ↑ 《Based on a computer model that predicted a peak internal temperature of 30 MeV (350 GK) during the merger of a binary neutron star system (which produces a gamma–ray burst). The neutron stars in the model were 1.2 and 1.6 solar masses respectively, were roughly 20 km in diameter, and were orbiting around their barycenter (common center of mass) at about 390 Hz during the last several milliseconds before they completely merged. The 350 GK portion was a small volume located at the pair's developing common core and varied from roughly 1 to 7 km across over a time span of around 5 ms. Imagine two city-sized objects of unimaginable density orbiting each other at the same frequency as the G4 musical note (the 28th white key on a piano). It's also noteworthy that at 350 GK, the average neutron has a vibrational speed of 30% the speed of light and a relativistic mass (m) 5% greater than its rest mass (m0).》.
- ↑ 《Results of research by Stefan Bathe using the PHENIX detector on the Relativistic Heavy Ion Collider at Brookhaven National Laboratory in Upton, New York, U.S.A. Bathe has studied gold-gold, deuteron-gold, and proton-proton collisions to test the theory of quantum chromodynamics, the theory of the strong force that holds atomic nuclei together.》.
- ↑ 《The Planck frequency equals 1.85487(14)×1043 Hz (which is the reciprocal of one Planck time). Photons at the Planck frequency have a wavelength of one Planck length. The Planck temperature of 1.41679(11)×1032 K equates to a calculated b /T = λmax wavelength of 2.04531(16)×10−26 nm. However, the actual peak emittance wavelength quantizes to the Planck length of 1.61624(12)×10−26 nm.》.
- ↑ 《Physical Review 81, 279》. 1951.
- ↑ Pertti Hakonen, Olli V. Lounasmaa (1994년 9월 23일). 《Science 265, 1821-1825》.
- ↑ [참고] 기상청, 실내 적정온도와 습도 Archived 2019년 1월 4일 - 웨이백 머신 (공공누리 오픈자료)
- ↑ [참고] 동아사이언스 - 겨울철 실내 적정온도 18~20도, 왜?
- ↑ 수질오염공정시험기준 ES 04000.d 총칙 2017























![{\displaystyle v=k[A]^{a}[B]^{b}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3bf8e9ff6eadfe7c1024188e943660bf2eeb440)






![{\displaystyle T_{eff}={\sqrt[{4}]{\frac {F}{\sigma }}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0772cec5973a12a2bbb2ec5010f8abbedbbf09f1)






