흑체
흑체(黑體, 영어: black body, 독일어: Schwarzer Körper)란 진동수와 입사각에 관계없이 입사하는 모든 전자기 복사를 흡수하는 이상적인 물체이다.
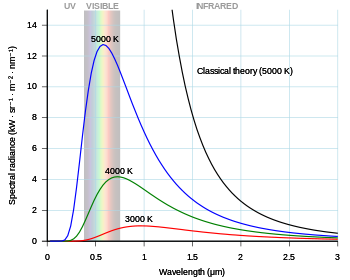
열평형 상태에 있는(즉, 온도가 일정한) 흑체는 "흑체복사"라는 전자기 복사를 방출한다. 이 복사는 플랑크 법칙에 따라 방출되며, 그것인즉 물체의 모양이나 구성요소가 아닌 온도에 의해서만 결정되는 스펙트럼을 가지고 있다는 것을 의미한다(우측 그림 참조).
열평형 상태의 흑체는 두 가지의 주요한 성질을 나타낸다.[1]
- 이상적 방출체이다. 모든 진동수에서 대상은 같은 온도의 그 어떠한 물체만큼, 또는 그 이상의 에너지를 방출한다.
- 확산성 방출체이다. 대상의 에너지는 등방적으로, 방향과 관계없이 복사된다.
대략적인 흑체면의 사례로는 단단히 둘러싸인 벽의 구멍을 들 수 있다. 구멍 속으로 들어간 빛은 영원히 반사를 반복하거나 구멍 내부에 흡수되어 다시 밖으로 나타나지 않는 것으로 보인다. 즉 이 구멍은 거의 완벽한 흡수체이다. 이렇게 둘러싸여 사방이 막힌 복사체는 벽의 성질과 구멍을 둘러싼 다른 성분들에 따라 열평형이 될 수도 있고 안 될 수도 있다.[2][3]
실제의 물질은 흑체 에너지 수준의 극히 일부(방사율이라 한다)의 에너지를 방출한다. 정의에 따르면, 열평형 상태의 흑체는 방사율이 ε = 1.0이다. 진동수와 관계없이 방사율이 이것보다 낮은 물질은 보통 회체(灰體, gray body)라 한다.[4][5] 방사율을 최대한 1에 가깝게 하여 흑체를 만들어내는 것은 현재까지도 주요한 관심대상으로 남아 있다.[6] 한편 백체(白體, white body)란 "모든 입사광선을 완벽히, 모든 방향으로 균일하게 반사하는 거친 면"이다.[7]
천문학에서, 항성과 행성의 복사를 유효온도에 관하여 나타내는 경우가 있다. 유효온도란 똑같은 양의 전자기 에너지 선속을 방출하는 흑체의 온도이다.
역사[편집]
흑체라는 개념은 1862년에 구스타프 키르히호프가 처음 사용했다.
흑체 복사[편집]
키르히호프의 복사법칙[편집]
"복사파의 분포가 물체의 종류에 따라 다르지 않고, 오직 온도에만 의존한다."
한 물체가 뜨거워지면 열을 내게 되는데, 이를 복사(radiation)라고 부른다. 고체에서 방출되는 복사를 조사하면 여러 가지 파장 또는 진동수를 가진 빛으로 구성되어 있음을 알 수 있다. 어느 물체나 그 표면에 부딪히는 복사열의 일부는 흡수하고 나머지는 반사한다. 특히 표면에 부딪히는 모든 복사를 흡수하는 경우 이런 물체를 흑체(black body)라고 부른다. 물론 흑체는 자신이 가지고 있는 열 즉 복사열을 방출도 한다. 19세기말에 물리학자들은 흑체에서 어떻게 여러 가지 진동수를 가진 복사가 나오며 이들은 표면의 온도와 어떠한 관계가 있는가를 많이 연구하였고 복사의 연구로부터 양자론이 시작되었다.
이런 흑체에 대한 연구의 시작은 1850년대부터로 생각할 수 있다. 1859년말에서 1860년초에 키르히호프(G. Kirchhoff, 1824-1887)는 '흑체복사강도의 분포는 벽의 물질이나 빈구멍(Cavity)의 모양, 크기와는 상관이 없고 오직 온도와 빛의 파장에만 관계된다는 것이다'는 것을 밝혔다. 즉, 같은 온도로 달구어진 물체는 돌이든 쇠든 방출하는 빛의 분포가 똑같다는 것이다.
하지만 당시의 실험이나 이론물리학 수준으로는 다양한 온도와 파장에 걸쳐 키르히호프가 정의한 열복사의 강도를 정확하게 기술하기란 쉬운 일이 아니었다.
슈테판 - 볼츠만 법칙[편집]
키르히호프가 복사법칙을 발견하였지만, 열복사 문제를 맥스웰의 전자기학과는 별개로 취급되는 등 당시의 이론물리학 수준으로는 키르히호프의 복사 법칙을 정확하게 기술하기에 어려움이 있었다.
1879년 오스트리아의 물리학자 요제프 슈테판(Josef Stefan, 1835-1893)이 실험적으로 전체 복사 에너지가 절대온도의 4제곱에 비례한다는 사실을 발견하였다. 1884년 오스트리아의 물리학자 루트비히 볼츠만이 슈테판의 공식을 맥스웰 방정식을 사용하여 유도하였다. 이 법칙을 오늘날 슈테판-볼츠만 법칙으로 부른다.
1886년 미국의 천문학자인 랭글리(S. P. Langley, 1834-1906)는 적외선의 강도를 잴 수 있는 볼로미터(bolometer)를 개발해서 흑체구리에서 발생하는 에너지와 태양에서 발생하는 에너지를 비교하는 실험을 통해 정량적인 흑체 복사 법칙을 발전시킬 수 있는 토대를 마련해 주었다. 볼로미터를 이용한 랭글리의 실험은 여러면에서 정성적이고 상당히 엉성한 것이었지만, 곧 여러사람들에 의하여, 실험적 차원에서 더욱 정교한 정량적 수준으로 발전했다. 그리고 1888년 하인리히 헤르츠가 전자기파의 존재를 발견한 뒤에야 많은 사람들은 가시 광선이나 열복사에 맥스웰의 전자기 법칙을 적용하기 시작할 수 있었다.
슈테판-볼츠만 법칙의 유도[편집]
동공 속의 에너지 밀도 u는 에너지 밀도를 모든 진동수에 대해 적분하여 얻을 수 있다.
여기서 는 보편적인 상수이다. 총 에너지 밀도는 동공 벽의 절대온도의 4제곱에 비례한다. 그러므로, 어떤 물체가 단위 시간당, 단위 면적당 복사하는 에너지 역시 에 비례한다고 기대할 수 있을 것이다. 이를 슈테판-볼츠만 법칙이라고 한다.
빈 변위 법칙[편집]
빈 변위 법칙은 흑체 복사의 파장 가운데 에너지 밀도가 가장 큰 파장과 흑체의 온도가 반비례한다는 것을 말하는 법칙이다.
레일리-진스 법칙[편집]
1900년 6월 존 윌리엄 스트럿 레일리는 위에서 주어진 빈의 미지함수 F가 상수임으로 보였는데, 고전물리학적 개념을 사용한 이 공식의 완전한 유도는 1905년 레일리와 진스(J. Jeans)에 의하여 이루어졌다. 흑체복사 스펙트럼을 설명하기 위해, 레일리와 진스는 흑체복사를 온도 T에서 복사가 채워진 공동 (cavity)으로 생각하는 것으로부터 시작하여 고전적인 계산을 하였다.
레일리-진스 법칙의 유도[편집]
방식(mode)의 수[편집]
흑체 내부의 밀폐된 빈 공간을 한 변의 길이가 A, B, C인 직육면체로 한다. 그리고 흑체 내부의 빈 공간과 그 벽면은 온도 T의 평형상태에 있다고 가정한다. 공동의 벽을 완전 반사체로 가정하였기 때문에 복사는 전자기파의 정상파로 되어 있어야만 한다. 각 벽 위에서 정상파의 마디가 형성되기 위해서는, 방향이야 어떻든 간에 벽과 벽 사이의 경로가 반 파장의 정수배가 되어야 할 것이다. 이 조건은 정상파의 x,y,z방향에 대한 가능한 파수들은 각각 다음과 같은 조건을 충족시킨다.
그리고 총 파수는 다음과 같은 식을 만족한다.
위의 식은 타원체(ellipsoid)의 방정식에 해당된다. 주어진 에 대하여 여러 개의 방식이 존재한다. 방식의 수를 얻기 위하여 먼저, 주어진 보다 작은 값을 갖는 방식의 수를 구하자.
이 값은 n,m,l으로 구성된 공간에서의 타원체의 제 1상한 부분(n,m,l값이 모두 양수인 공간)의 부피에 해당한다. 빛은 두 개의 자유도를 가지므로, 그 부피에 2배를 함으로써 얻을 수 있다. 가 주어진면 타원체의 긴반지름과 짧은반지름이 각각 이므로
(총 방식의 수) =
를 얻는다. 한편 직육면체의 부피는 V = ABC 이므로 단위 체적당 진동수가 에서 사이에 있는 방식의 수는
가 된다.
- 는 각진동수이고 진동수 이므로, 단위 부피 안에서 진동수가 와 사이에 있는 방식의 수는
가 된다.
에너지 밀도[편집]
다음 단계는 각 정상파당의 평균 에너지를 구하는 것이다. 여기에 양자 물리와 고전물리 사이에 차이가 벌어진다. 이미 언급했던 고전적인 에너지의 등분배 법칙을 따르면 온도 T에서 열적 평형을 이루고 있는 어떤 개체로 이루어진 계에서 각 자유도에 배당되는 평균 에너지는 1/2kT이다. 복사로 가득 찬 공동 내에서의 정상파는 평균 총 에너지로 E=kT를 주는 두 개의 자유도를 가진다. 왜냐하면, 각 파는 공동의 벽안에 있는 한 진동자로부터 발생되기 때문이다. 이러한 진동자는 두 개의 자유도를 가지는데, 하나는 진동자의 운동 에너지에, 나머지 하나는 진동자의 위치 에너지에 해당된다.
여러 개의 단진자가 온도 T에서 열적 평형 상태를 이루고 있다면 단위 부피 안에 에너지 E를 갖는 진동자의 수는 볼츠만 분포를 따른다고 생각하여 에너지가 E~E+dE사이에 있는 경우 진동자의 수 이다. 따라서 만일 에너지가 연속적으로 변하는 경우 한 진동자가 가지는 평균 에너지는
이다. 여기서 1/kT = 로 두고, 분배 함수 를 다음과 같이 정의하자.
그렇다면 한 진동자가 가지는 평균 에너지를 분배 함수를 사용하여 다음과 같이 나타낼 수 있다.
레일리와 진스는 각 모드가 kT의 에너지를 갖기 때문에 구하려는 복사에너지의 밀도는 주어진 모-드의 수에 kT를 곱하여 얻을 수 있다고 생각하였다. 따라서 진동수 사이에 있는 복사에너지 밀도는 의 결과를 얻는다. 이 식은 진동수가 작은 영역에서는 잘 맞으나 진동수가 큰 영역에서는 맞지 않는다. 만약 진동수가 가 되면 에너지 밀도역시 가 된다. 이 경우를 자외선 파탄(ultraviolet catastrophe)라 부르며 막스 플랑크는 이것의 보완을 고려하였다.
플랑크의 복사 법칙[편집]
1900년 12월, 플랑크는 흑체 복사의 측정 자료와 일치하는 결과를 얻기 위하여 방출된 빛의 에너지가 특정한 상수(h)와 진동수를 곱한 값의 정수배로만 주어진다고 가정하였다.
여기서 방출된 빛의 에너지가 연속적이지 않고, 어떤 기본 에너지 양자 의 정수배로만 주어진다는 가정은 빛이 파동으로서 그 에너지가 연속적 값을 갖는다는 고전적 개념과 배치되며 우리는 이러한 가정을 플랑크의 양자가설(Quantum hypothesis)이라고 한다. 이 경우 방출된 빛의 평균 에너지는 다음과 같다
여기서, 로 치환하고, 분배 함수 Z를 다음과 같이 정의하면
빛의 평균 에너지를 다음과 같이 나타낼 수 있다.
따라서 진동자 당 평균에너지는 레일리-진스 공식에서 사용하였던 에너지 등분배 평균인 kT 대신에 아래와 같이 된다.
여기에 단위 체적당 방식 밀도를 곱하면 전자파의 에너지 밀도에 대한 플랑크 법칙
을 얻는다.
플랑크가 올바른 공식을 얻기는 하였지만, 오늘날의 시각으로 보면 그의 공식 유도에는 심각한 결함이 내포되어 있다. 오늘날 우리는 공동 벽에 있는 진동자는 그 에너지로 가 아닌 을 가짐을 알고 있다. 영점 에너지 을 포함하여 맥스웰-볼츠만 통계를 적용하면 위의 플랑크 평균 에너지 밀도식이 주어 지지 않는다. 정당한 절차는 공동내의 전자기파를 광자 가스로 생각하고, 광자의 스핀이 1이므로 보즈-아인슈타인 통계를 적용한다. 그러므로, 각 에너지 상태 에 있는 평균 광자수는 아래 식의 보스-아인슈타인 분포에 의해 주어진다.
- 보스-아인슈타인 분포함수
- 막스 플랑크와 물리학의 혁명
막스플랑크가 자신의 생애에서 보여주었던 양자 불연속성 개념에 대한 태도는 매우 복잡하다. 우선 작용 양자에 대한 개념을 제창해서 양자물리학의 포문을 열었던 막스 플랑크 자신은 이런 변혁이 혁명으로 발전하기를 원하지 않았다. 즉 20세기 초 현대 물리학 분야에서 나타난 혁명적 변화는 정작 창시자였던 막스 플랑크 자신은 원하지 않았던 혁명이었다. 플랑크는 아주 보수적인 인물로서 본래 고전물리학을 거부할 의사가 추호도 없었던 사람이었다. 그는 아인슈타인의 상대성 이론은 높이 평가했지만, 정작 자신의 업적과 관련이 있었던 아인슈타인의 광양자 가설에 대해서는 깊은 회의를 나타냈던 인물이었다. 또한 고전 양자론의 시작을 알렸던 그는 고전양자론의 발전 과정에서 나온 마지막 산물인 양자역학의 철학적 해석인 비결정론에 대해서도 아인슈타인과 마찬가지로 죽을 때까지 받아들이지 않았다. 한편 지난 세기말에 이룩한 플랑크의 혁명은 여러 가지로 우리에게 시사하는 바가 크다. 우선 플랑크의 이 혁명은 물리학이 너무 완벽하게 완성되어 더 이상 할 일이 없을 것 같은 상태에서 나타났다는 것이다. 만약 플랑크가 뮌헨 대학시절 교수에게 설득되었다면 그는 새로운 혁명적 이론을 제기한 이론 물리학자로 역사에 남지 않았을 것이다. 더 이상 새롭게 할 일이 없는 것 같은 답답한 상황이 바로 혁명이 시작되는 시점이었다. 또한 플랑크는 혁명적 이론을 제안한 다른 많은 과학자들과는 달리 그리 천재적인 인물은 아니었다는 것도 흥미롭다. 20세기 초 물리학내의 혁명은 보이지 않는 곳에서 성실하게 일했던 대기만성형의 평범한 과학자에 의해서 시작되었던 것이다.
참고 문헌[편집]
- Kelly, Robert E. (1981년 8월). “Thermodynamics of blackbody radiation” (PDF). 《American Journal of Physics》 49 (8): 714. doi:10.1119/1.12416. 2009년 9월 20일에 원본 문서 (PDF)에서 보존된 문서. 2012년 10월 29일에 확인함.
- ↑ Mahmoud Massoud (2005). "§2.1 Blackbody radiation". Engineering thermofluids: thermodynamics, fluid mechanics, and heat transfer. Springer. p. 568. ISBN 3-540-22292-8.
- ↑ The approach to thermal equilibrium of the radiation in the cavity can be catalyzed by adding a small piece of matter capable of radiating and absorbing at all frequencies. See Peter Theodore Landsberg. Thermodynamics and statistical mechanics (Reprint of Oxford University Press 1978 ed.). Courier Dover Publications. p. 209. ISBN 0-486-66493-7.
- ↑ Planck 1914, p. 44, §52
- ↑ The emissivity of a surface in principle depends upon frequency, angle of view, and temperature. However, by definition, the radiation from a gray body is simply proportional to that of a black body at the same temperature, so its emissivity does not depend upon frequency (or, equivalently, wavelength). See Massoud Kaviany (2002). "Figure 4.3(b): Behaviors of a gray (no wavelength dependence), diffuse (no directional dependence) and opaque (no transmission) surface". Principles of heat transfer. Wiley-IEEE. p. 381. ISBN 0-471-43463-9. and Ronald G. Driggers (2003). Encyclopedia of optical engineering, Volume 3. CRC Press. p. 2303. ISBN 0-8247-4252-4.
- ↑ Some authors describe sources of infrared radiation with emissivity greater than approximately 0.99 as a black body. See “What is a Blackbody and Infrared Radiation?”. 《Education/Reference tab》. Electro Optical Industries, Inc. 2008. 2016년 3월 7일에 원본 문서에서 보존된 문서. 2019년 6월 7일에 확인함.
- ↑ Ai Lin Chun (25 Jan 2008). "Carbon nanotubes: Blacker than black". Nature Nanotechnology. doi:10.1038/nnano.2008.29.
- ↑ 방사율 약 0.99 초과의 적외선 복사원을 흑체라고 하는 사람들도 있다. 다음을 참조. "What is a Blackbody and Infrared Radiation?" Archived 2016년 3월 7일 - 웨이백 머신. Education/Reference tab. Electro Optical Industries, Inc. 2008.























































