아르키메데스
| 아르키메데스 | |
|---|---|
 〈아르키메데스의 초상〉 앙드레 테베의 삽화집(1586년)에서 | |
| 출생 | 약 기원전 287년 시라쿠사 |
| 사망 | 약 기원전 212년 시라쿠사 |
| 성별 | 남성 |
| 국적 | 마그나 그라이키아 |
| 직업 | 철학자, 수학자, 공학자 |
아르키메데스(고대 그리스어: Ἀρχιμήδης, 현대 그리스어: Αρχιμήδης 아르히미디스, 기원전 287년 경 ~ 기원전 212년 경)는 고대 그리스 마그나 그라이키아의 일부였던 시라쿠사 출신의 철학자, 수학자, 천문학자, 물리학자 겸 공학자이다. 그의 생에 대해 남겨진 기록은 얼마 되지 않으나 고전 고대의 대표적인 과학자, 수학자로 손꼽히고 있다. 아르키메데스는 물리학 분야에서 정역학과 유체정역학을 연구했으며 지레의 원리를 설명한 것으로 잘 알려져 있다. 또한 아르키메데스는 아르키메데스 나선양수기, 해상에 있는 배를 공격하기 위한 거울 등의 기계를 제작하기도 하였다.
아르키메데스는 고전 고대 시기의 가장 뛰어난 수학자 가운데 한 명으로도 평가받고 있다.[1][2] 수학과 관련한 아르키메데스의 업적으로는 십진법의 도입, 포물선으로 둘러싸인 도형의 넓이 계산, 원주율의 계산과 같은 것들이 있다.[3]
생애[편집]


아르키메데스는 기원전 287년 무렵 시라쿠사에서 태어났다. 시칠리아에 있는 도시인 시라쿠사는 아르키메데스가 태어날 무렵 마그나 그라이키아의 자치 식민지였다. 아르키메데스의 출생 연도는 비잔틴 그리스의 역사가 존 체체스의 연표에 기초한 것이다. 체체스는 아르키메데스 사망 당시 나이가 75세라는 기록을 근거로 그의 출생년도를 산정하였다.[4]
아르키메데스의 생애에 대해서는 그의 출생지와 죽음 이외에 알려진 사실이 그리 많지 않다. 발견의 기쁨에 벌거벗고 거리를 달렸다는 것 같은 아르키메데스와 관련한 많은 일화는 후대에 각색된 것이다. 아르키메데스는 스스로를 수학자이자 철학자로 여겼고 특히 구에 대한 자신의 발견을 자랑스럽게 생각하였다.[5]:17–28
아르키메데스는 《모래알을 세는 사람》에서 아버지에 대해 간략히 언급하였는데, 이름이 피디아스라는 것과 천문학자라는 점 외에는 알려진 바가 없다. 플루타르코스 영웅전에서는 아르키메데스가 시라쿠사의 국왕 히에론 2세와 친척이었다고 서술하고 있다.[6] 다른 기록으로는 아르키메데스의 친구였던 헤라클레이데스가 쓴 전기가 있었으나 소실되었다.[7] 이 때문에 아르키메데스가 결혼은 했는지, 아이가 있었는지와 같은 것은 알 수 없게 되었다. 그나마 알려진 것으로는 아르키메데스가 청년기에 알렉산드리아와 이집트에서 공부하였다는 것과, 사모스의 코논, 에라토스테네스와 같은 사람들과 동시대에 살았다는 것 정도이다. 아르키메데스는 도시데우스에게 다음과 같은 편지를 썼다.[5]:87
저는 옛 친구였던 코논이 죽었다는 비보를 듣고 친구이자 평소 존경했던 한 수학자를 잃었다는 슬픔에 잠을 못 이루었습니다. 지금까지 누구에 의해서도 연구된 적이 없고 마침내 저에 의해 완성된 한 정리를 코논에게 보낼 작정이었는데 이제 보낼 수가 없게 되어버렸군요.
아르키메데스는 기원전 212년 무렵 제2차 포에니 전쟁 중에 사망하였다.기원전 212년 로마의 장군 마르쿠스 클라우디우스 마르켈루스는 2년 동안의 공방전 끝에 시라쿠사를 점령하였다. 플루타르코스 영웅전에 따르면 도시가 함락될 당시 아르키메데스는 기하학 문제를 놓고 고심하고 있었다고 한다. 시라쿠사가 함락되자 로마 군인이 아르키메데스에게 찾아와 마르켈루스를 접견하라고 명령하였다. 아르키메데스가 문제를 푸는 도중이라며 거절하자 이에 격분한 군인이 아르키메데스를 칼로 찔러 살해하였다고 한다. 플루타코스는 이 외에도 아르키메데스의 사망에 대한 다른 이야기를 소개하고 있는데, 아르키메데스가 도시 함락 와중에 사망한 것일 수도 있다고 덧붙였다. 아르키메데스가 들고 있던 해시계, 구와 같은 도구가 보물로 오인되어 이를 약탈하려는 병사에 의해 살해되었다는 것이다. 마르켈루스 장군은 도시를 함락시키면서 부하들에게 아르키메데스의 안전을 당부하였기 때문에 그의 사망 소식에 매우 화를 냈다고 한다.[8]
한편, 아르키메데스가 남긴 말로 유명한 “내 원을 건드리지마 ” (그리스어: μὴ μου τοὺς κύκλους τάραττε, 라틴어: Noli turbare circulos meos)는 후대에 누군가가 지어낸 것으로 플루타르코스 영웅전에서는 언급되지 않는다.[8] 폴리비오스는 《세계 역사》에서 시라쿠사 공방전과 아르키메데스의 죽음을 언급하였다. 플루타르코스와 티투스 리비우스의 저서를 바탕으로 폴리비우스는 아르키메데스가 도시 방어를 위해 여러 가지 기계를 제작한 기술자였다고 적고 있다.[9]
아르키메데스가 사망한 지 137년이 지난 기원전 75년 키케로는 시라쿠사의 재무관으로 임명되었다. 키케로는 자신이 알고 있던 아르키메데스의 무덤에 대한 이야기를 확인하기 위해 사방으로 찾아다닌 끝에 시라쿠사 인근의 관목 사이에 버려져있던 묘비를 발견하였다. 키케로는 아르키메데스의 묘비에는 원기둥과 구가 그려져있다는 이야기를 바탕으로 자신이 찾은 묘가 아르키메데스의 것이라 확신하였다.[10]
아르키메데스의 묘비에는 그가 증명한 같은 높이의 원기둥과 구의 부피 관계를 나타내는 그림이 새겨졌다. 아르키메데스는 구의 부피는 같은 높이의 원기둥의 부피에 대해 3분의 2이라는 것을 증명하였다. 간단히 두 도형의 부피를 비교하면 반지름이, r인 구의 부피는
- s
이고, 이 때 같은 높이를 갖는 원기둥의 밑변은 반지름이 r인 원이 되고 높이는 2r이므로 원기둥의 부피는
- c
이다. 따라서
- Vs: Vc
이 되므로 구의 부피는 같은 높이의 원기둥에 대해 언제나 3분의 2가 된다.
발견과 발명[편집]
금관[편집]

가장 널리 알려진 아르키메데스의 일화는 불규칙한 물체의 부피를 측정하는 방법을 발견한 것이다. 이에 대해 비트루비우스는 다음과 같이 기록하고 있다. 히에론 2세는 금세공사에게 순금을 주어 신에게 바칠 금관을 만들게 하였다. 완성된 금관을 받은 히에론 2세는 은이 섞인 것이 아닌가 의심하였으나 확인할 여지가 없어 아르키메데스에게 의뢰하였다.[11] 아르키메데스는 사람이 욕조에 들어가면 물이 차오르는 것에 착안하여 물질의 밀도에 따라 비중이 다르다는 것을 발견하였다. 즉 서로 다른 물질은 같은 무게라 할 지라도 차지하는 부피가 다르므로 물통에 집어 넣었을 때 서로 다른 비중을 가지게 된다.[12] 이것을 깨닫게 된 아르키메데스는 옷을 입는 것도 잊고 뛰쳐나와 “찾았다”(그리스어: εὕρηκα!)[주해 1]를 외쳤다고 한다. 왕관과 같은 무게의 금을 비교한 실험으로 아르키메데스는 금세공사가 속임수를 썼다는 것을 증명할 수 있었다.[13] 다면체가 갖는 부력에 대한 정리는 아르키메데스의 원리로 알려져 있다.
아르키메데스 나선양수기[편집]

아르키메데스가 제작한 기계들은 대부분 그의 고향인 시라쿠사의 일상 생활에 도움이 되기 위한 것이었다. 그리스의 작가 아테나에우스는 아르키메데스가 히에론2세의 부탁을 받아 거대한 선박을 제작하였다고 기록하였다. 시라쿠시아라고 이름이 붙여진 이 선박은 고대 그리스 시대에 가장 큰 수송선이었다. 아테나에우스에 따르면 시라쿠시아에는 정원과 아프로디테 신전이 딸려 있었으며 600여 명이 승선할 수 있었다고 한다. 선저에 물이 차면 아르키메데스 나선양수기를 이용하여 배출하였다. 속이 빈 긴 원기둥에 회전축을 두고 나선을 붙인 아르키메데스 나선양수기는 회전축을 돌려 물을 퍼 올리는 기구이다. 이 양수기는 오늘날에도 쓰이고 있다.[14] 로마 시대의 작가 비트루비우스는 아르키메데스 나선양수기가 바빌로니아의 공중 정원에서 사용되었던 나선양수기를 개량한 것이라고 기록하였다.[15][16][17] 1839년 건조된 세계 최초의 프로펠러 추진 방식의 증기선은 아르키메데스의 업적을 기려 아르키메데스로 명명되었다.[18]
아르키메데스 갈고리[편집]
무거운 금속 갈고리를 단 밧줄을 지레에 연결한 아르키메데스 갈고리는 연안에 접근하여 상륙하려는 적선을 막는 방어용 무기였다. 자세한 구조는 알려져 있지 않으나 다가오는 배를 향해 갈고리를 던져 건 다음 지레를 이용하여 배를 전복시켰다고 한다.[19][20]
아르키메데스 거울[편집]

여러 거울에 반사된 햇볕을 적선에 집중하여 불을 붙인다.
2세기 무렵 고대 로마의 작가 루키아노스는 시라쿠사 공방전에서 아르키메데스가 로마의 전함을 불태웠다고 기록하였다. 고대 그리스의 수학자였던 트랄레스의 안테미우스는 아르키메데스가 사용한 무기가 일종의 화경이었다고 언급하였다.[21] 아르키메데스 열선이라고도 불리는 이 무기는 햇볕을 한 데 모아 불을 붙이는 기구였다. 이러한 무기로 공격이 가능한 지에 대해서는 르네상스 시대까지 논란이 되었다. 르네 데카르트는 실제 그런 무기가 만들어지지 않았을 것이라 여겼지만 근대에 들어 존 웨슬리 등은 당시에도 그런 무기의 제작이 가능하였을 것이란 의견을 피력하였다.[22]
구리나 청동으로 제작된 거울을 포물면 반사판과 같이 배치하여 초점 거리를 적절히 조정하면 실제 불을 붙일 수 있다. 오늘날에도 이러한 원리를 이용하여 태양로가 만들어지고 있다. 1973년 그리스의 과학자 로아니스 사카스는 실제 실험을 통해 아르키메데스 거울을 재현하였다. 그는 50미터 거리를 둔 모형 로마 범선을 향해 가로 1.5 미터 세로 1 미터의 거울 70개로 햇볕을 모아 불을 붙이는데 성공하였다. 이 실험에서 모형 범선은 초점이 모아진지 수 초 만에 불꽃을 일으켰다. 당시 로마 범선에 이용된 타르는 발화제로 작용하였을 것이다.[23]
2005년 메사추세츠 공과대학의 학생들은 1평방피트의 거울 127개로 아르키메데스 거울을 재현하여 30미터 떨어진 모형 배에 불을 붙이는 실험을 하였다. 이 실험에서는 햇볕이 초점에 모인 뒤 배에 연기가 나기 시작하였으나 구름이 햇볕을 가리는 바람에 불을 붙이는 데는 실패하였다. 아르키메데스 거울을 무기로 사용하는 것은 날씨에 크게 좌우될 수 밖에 없다. MIT 학생들의 이 실험은 후에 텔레비전 프로그램 호기심 해결사에서 다시 시도되었는데 샌프란시스코에서 낚시 보트를 놓고 진행된 이 실험에서는 배에 불꽃을 일으켰다.[24][주해 2] 나무가 불이 붙기 시작하는 발화점은 약 300 °C다.[25][26]
한편, 아르키메데스가 이러한 무기를 실제로 제작하여 사용하지는 않았을 것이라는 의견도 있다. 컬럼비아 대학교의 수학과 교수인 셔먼 스타인은 아르키메데스의 거울 무기는 후대에 지어낸 이야기라고 판단하고 있는데, 왜냐하면 그러한 무기가 선박을 향한 공격에 효과적이었다면 후대에 다른 전투에서도 사용되었을 것인데 그러한 기록은 발견되지 않기 때문이다.[주해 3]
기타[편집]
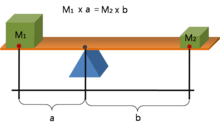
지레에 올린 두 물체가 받침점에서 떨어진 거리와 무게의 곱이 같을 때 지레는 정적 평형 상태가 된다.
아르키메데스는 《평면의 균형》에서 지레의 여러 원리를 밝혔다.[27] 고대 그리스에서는 아르키메데스 이외에도 아리스토텔레스와 그의 학파에서 연구하였던 아르키타스 등이 지레의 원리를 연구하였다.[28] 알렉산드리아의 파푸스가 쓴 기록에 따르면, 아르키메데스는 “적당한 장소가 주어진다면 지구라도 들어보이겠다”(그리스어: δῶς μοι πᾶ στῶ καὶ τὰν γᾶν κινάσω)라고 말하였다고 한다.[29] 플루타르코스는 아르키메데스가 복합 도르래와 지레를 이용하여 배에서 무거운 물건을 옮길 수 있는 장치를 발명하였다고 적고 있다.[30] 이 외에도 아르키메데스는 사거리의 조정이 가능한 투석기와 주행거리계를 제작하였다. 톱니바퀴를 이용한 주행거리계는 오늘날 자동차에서도 사용된다.[31]
키케로는 대화록 《국가에 대해》(라틴어: De re publica)에서 아르키메데스의 발명을 언급하고 있다. 키케로는 시라쿠사가 함락된 후 7년이 지난 기원전 219년 로마를 배경으로 가상의 대화를 집필하였는데, 여기서 마르쿠스 클라우디우스 마르켈루스는 시라쿠사를 함락시킨 뒤 태양과 달, 그리고 다섯개의 행성의 움직임을 보여주는 천체 모형 두 개를 로마로 가져왔다고 말하고 있다. 키케로는 이 모형들이 원래 탈레스와 에우독수스에 의해 고안된 것이라 언급하고 있다. 대화록에서 마르셀루스는 천체 모형 가운데 한 개는 전리품으로 자신이 소장하고 다른 하나는 덕의 여신 사원에 기증하였다고 말한다. 키케로는 마르셀루스가 로마의 두 집정관 가이우스 술피시우스 갈루스와 루시우스 푸리우스 필루스 앞에서 천체 모형을 동작시켜 보였다고 적고 있다.
Hanc sphaeram Gallus cum moveret, fiebat ut soli luna totidem conversionibus in aere illo quot diebus in ipso caelo succederet, ex quo et in caelo sphaera solis fieret eadem illa defectio, et incideret luna tum in eam metam quae esset umbra terrae, cum sol e regione.
갈리우스가 지구를 돌리자 실제 하늘에서 그러하듯이 청동으로 만들어진 달과 태양이 몇 바퀴씩 회전하였다. 태양이 지구의 그림자로 들어가면 달이 자신의 위치로 모습을 드러내었다.[32][33]
키케로의 설명은 플라네타리움이나 태양계의를 묘사하고 있는 것으로 보인다. 알렉산드리아의 파푸스는 아르키메데스의 저작 《구체에 대해》에서 이러한 기계의 작동 방식을 설명하고 있다고 기록하고 있다. 아르키메데스의 이 저작은 소실되었다. 근대에 발견된 고대 안티키테라 기계는 차동 톱니바퀴를 사용한 일종의 계산기로 추정되고 있는데[34], 키케로가 언급하고 있는 천체 모형 역시 이와 같은 방식으로 작동되었을 것이다.[35][36]
수학[편집]

아르키메데스는 수학에서도 여러 업적을 남겼다. 플루타르코스는 그의 책에서 “아르키메데스는 저급한 삶의 욕구에서 비롯되지 않은 순수한 사색에 모든 역량과 야망을 쏟아 부었다.”라고 평했다.[37]
무리수의 계산[편집]
아르키메데스는 근대 적분이 없었던 당시에 무한소수의 개념을 사용하였다. 그는 소거법을 사용하여 의 근삿값을 계산하였다. 이 방법은 임의 차원의 미지항에 대해 극한을 취하는 것으로, 귀류법을 사용하여 동일한 계산을 반복하는 과정을 통해 해답을 얻는 것이다. 아르키메데스는 매우 많은 변을 갖는 다각형이 임의의 원에 내접하는 경우와 외접하는 경우를 비교하여 원주율을 계산하였다. 즉, 임의의 원의 둘레는 그것에 외접하는 다각형의 둘레보다 짧고 내접하는 다각형보다 길다. 이 때 다각형의 변이 많아질 수록 외접하는 경우와 내접하는 경우의 둘레 차는 작아지므로 원의 둘레에 근사하게 된다. 아르키메데스는 정구십육각형을 이용하여 의 값을 다음과 같이 계산하였다.[38]
아르키메데스는 이 결과에 따라 의 근삿값으로 3.1416을 제시하였다.[주해 4] 또한, 아르키메데스는 원의 면적이 임을 증명하였다. 아르키메데스는 그의 저서 《구와 원기둥》에서 어떠한 크기가 주어지더라도 임의의 크기에 적당한 수들을 곱하여 주어진 크기를 초과할 수 있다고 가정하였다. 이를 실수에서의 아르키메데스 성질이라고 한다.[39]
아르키메데스는 《원의 측정》에서 3의 제곱근을 다음과 같이 계산하였다.
아르키메데스의 이 계산은 매우 정확한 것이다. 하지만 그는 계산과정을 따로 밝히지는 않았다. 17세기 영국의 수학자 존 월리스는 “아르키메데스는 적분 계산법의 비밀을 후대에 넘겨주는데 너무나도 인색하였다”고 아쉬워하였다.[40]
도형의 넓이[편집]


아르키메데스는 《포물선의 구적법》에서 오른쪽의 그림과 같이 포물선과 직선으로 둘러싸인 도형의 넓이는 그에 내접하는 삼각형의 넓이에 대해 4⁄3이 된다는 것을 증명하였다. 아르키메데스의 증명 과정을 간략히 소개하면,
- 포물선을 가로지르는 직선을 한 변으로 하는 내접 삼각형을 그린다.
- 위와 같이 하여 그린 내접 삼각형에 의해 포물선은 두 구간으로 분할되며 여기에 다시 같은 방법으로 내접 삼각형을 그릴 수 있다.
- 이렇게 계속하여 내접 삼각형을 그려나가면 오른쪽 아래의 그림과 같이 포물선을 가로지르는 직선에 둘러싸인 도형은 무수히 많은 삼각형으로 분할된다.
- 최초의 내접 삼각형 넓이를 '1'이라고 하면 전체 삼각형의 넓이는 다음의 공식에 의해 구할 수 있다.
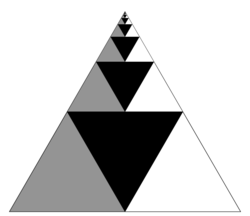
지속적으로 분할되는 도형의 넓이를 모두 합하여 급수로 표현하는 것을 기하급수라고 한다. 위의 식에 표현된 기하급수의 공비(公比)는 1⁄4이다. 이 기하급수의 값을 증명하는 방법은 여러 가지가 있으나 여기서는 직관적으로 이해하기 쉬운 《수학 매거진》1999년 2월호[41]에 실린 그림을 소개한다.
|
|
매우 큰 수의 표현[편집]
《모래알을 세는 사람》에서 아르키메데스는 온세상에 있는 모래알의 개수를 추정하는 방법을 소개하고 있다. 그는 연속적으로 셀 수 있는 것이라면 아무리 큰 수라도 표현할 수 있다고 생각하였다. 아르키메데스는 다음과 같이 서술하였다.
- “겔론 국왕은 모래알이 너무나 많기 때문에 무한한 것이라고 생각하였다. 그러나, 시라쿠사나 시칠리아 뿐만 아니라 지구 전체, 더 나아가 우주 전체를 모래알로 채운다고 하더라도 셀 수 있다. 수가 많다고 무한이라고 하는 것은 큰 수에 대해 아직 이름을 붙일 방법을 생각해내지 못했기 때문이다. 그러나 적당히 수를 부를 방법만 안다면 땅 전체의 무게나 제 아무리 깊은 바다의 깊이, 또는 가장 높은 산의 높이도 측정할 수 있다. 뿐만 아니라 적당한 단위로 묶어서 센다면 그의 곱셈을 통해 제아무리 많은 모래알의 개수도 신속하게 셈할 수 있다. 나는 이것을 사람들이 인정할 수 있도록 기하학으로 증명하려 한다. 큰 수를 부르는 방법은 일전에 내가 제우시푸스에게 제시하였던 방법을 따를 것이다. 이 방법에 의하면 지구 전체를 채울 모래알의 수 뿐만 아니라 우주 전체를 채울 모래알의 수도 계산할 수 있다." — Archimedis Syracusani Arenarius & Dimensio Circuli”
아르키메데스는 이 문제를 해결하기 위해 수를 만의 제곱의 배수로 표현하는 방법을 고안하였다. 이 방법에 따르면 1억은 1만의 만배, 즉 10,0002로 나타낼 수 있다. 아르키메데스는 온세상에 있는 모래알의 전체 개수는 대략 8×1063 개라고 추정하였다.[42]
주요 저서[편집]

아르키메데스의 저서는 도리아 방언으로 쓰여졌다.[43] 에우클레이데스의 저작들이 비교적 잘 보존되어 온 것에 비해 아르키메데스의 저작들은 대부분 소실되었다. 다른 학자들의 언급을 통해 확인할 수 있는 아르키메데스의 저작은 얼마 되지 않는다. 알렉산드리아의 파포스는 아르키메데스가 《구의 제작에 대해》와 다른 다면체에 대한 저서를 남겼다고 언급하였으나 지금은 전하지 않는다. 파푸스와 같은 시기의 학자인 알렉산드리아의 테온은 아르키메데스의 《굴절에 대해》를 인용하여 빛의 굴절을 소개하였는데 이 저서 또한 소실되었다. 이후에 그의 저작들은 비잔티움 제국, 이슬람 세계 등을 통해 전파되어 그리스어나 아랍어 등으로 번역되어 전해졌고, 르네상스 무렵 유럽에 소개되어 라틴어로 번역되었다.[44]
소실되었던 아르키메데스의 저작이 근대에 다시 발견된 경우도 있다. 1906년 덴마크의 수학사학자 하이베르그는 이스탄불에서 《부체(浮體)에 대하여》와 같은 글이 수록된 아르키메데스의 저서 《수학 정리의 방법》을 발견하였다. 이 저서는 다시 사라졌다가 1998년 10월 29일 뉴욕 크리스티 경매장에서 경매에 붙여졌다. 동방 정교회가 약탈 문화재에 대한 반환을 요구하였으나 미국 법원은 이를 기각하였고 익명의 수집가가 소유하게 되었다. 이 저서는 몇 차례 소유주가 바뀐 뒤 1999년 2월 일반에게 공개되었다.[5]:57–66
지금까지 전해오는 아르키메데스의 저작으로는 다음과 같은 것이 있다.
- 《평면의 균형에 대해》 - 평면 도형의 무게 중심을 찾는 방법을 정리한 저서이다.
- 《원의 측정에 대해》 - 《원의 측정에 대해》에서 아르키메데스는 소거법을 이용하여 원주율을 계산하였다.
- 《나선에 대해》 - 나선 곡선이 갖는 여러 성질을 연구한 저서이다.
- 《구와 원기둥에 대해》 - 《구와 원기둥에 대해》에서 아르키메데스는 같은 높이의 구와 원기둥이 갖는 부피의 비율을 정리하였다.
- 《원뿔의 단면에 대해》 - 원뿔을 잘랐을 때 나타나는 원, 타원, 포물선에 대해 정리한 저서이다.
- 《부체에 대해》- 다면체를 물에 띄웠을 때 무게 중심과 균형을 정리하였다.
- 《포물선의 구적법》 - 포물선과 직선으로 둘러쌓인 도형의 넓이는 그에 내접하는 삼각형의 넓이에 대해 4/3이 된다는 것을 증명하였다.
- 《오스토마치온》 - 아르키메데스의 상자라고도 불리는 오스토마치온은 칠교와 같이 정사각형을 여러 개의 도형으로 분할 한 퍼즐이다.
- 《아르키메데스의 가축 문제》- 아르키메데스는 일종의 디오판토스 방정식 문제인 가축 문제를 만들어 내었다. 이 부정 다항 방정식의 해는 매우 큰 수로, 아르키메데스는 동시대의 수학자 아폴로니우스에게 복수하기 위해 이 문제를 처음으로 제시하였다.[45] 1880년 계산된 아르키메데스 가축문제의 답은 7.760271×10206544이다.[46]
- 《모래알을 세는 사람》- 해변에 있는 모래알의 개수와 같은 매우 큰 수를 10,000의 거듭제곱으로 나타내는 방법을 정리하였다.
- 《수학 정리의 방법》- 부체에 대해, 가축 문제, 모래알을 세는 방법 등이 수록된 저서이다.
같이 보기[편집]
각주[편집]
- ↑ Calinger, Ronald (1999). A Contextual History of Mathematics. Prentice-Hall. p. 150. ISBN 0-02-318285-7. "Shortly after Euclid, compiler of the definitive textbook, came Archimedes of Syracuse (ca. 287 212 BC), the most original and profound mathematician of antiquity."
- ↑ O’Connor, John J.; Robertson, Edmund F. (1999년 1월). “Archimedes of Syracuse”. 《MacTutor History of Mathematics Archive》 (영어). 세인트앤드루스 대학교.
- ↑ O'Connor, J.J. and Robertson, E.F. (February 1996). "A history of calculus" Archived 2007년 7월 15일 - 웨이백 머신. University of St Andrews. Retrieved 2007-08-07.
- ↑ Heath, T. L., Works of Archimedes, 1897
- ↑ 가 나 다 Stein, Sherman (2006). 《아르키메데스》. 번역 이우영. 경문사. ISBN 89-7282-926-9.
- ↑ Plutarch. "Parallel Lives Complete e-text from Gutenberg.org". Project Gutenberg. Retrieved 2007-07-23.
- ↑ O'Connor, J.J. and Robertson, E.F.. "Archimedes of Syracuse". University of St Andrews. Retrieved 2007-01-02.
- ↑ 가 나 Rorres, Chris. "Death of Archimedes: Sources". Courant Institute of Mathematical Sciences. Retrieved 2007-01-02.
- ↑ Rorres, Chris. "Siege of Syracuse". Courant Institute of Mathematical Sciences. Retrieved 2007-07-23.
- ↑ Rorres, Chris. "Tomb of Archimedes: Sources". Courant Institute of Mathematical Sciences. Retrieved 2007-01-02.
- ↑ Vitruvius. "De Architectura, Book IX, paragraphs 9–12, text in English and Latin". University of Chicago. Retrieved 2007-08-30.
- ↑ "Incompressibility of Water". Harvard University. Retrieved 2008-02-27.
- ↑ HyperPhysics. "Buoyancy". Georgia State University. Retrieved 2007-07-23.
- ↑ Casson, Lionel (1971). Ships and Seamanship in the Ancient World. Princeton University Press. ISBN 0-691-03536-9.
- ↑ Dalley, Stephanie. Oleson, John Peter. "Sennacherib, Archimedes, and the Water Screw: The Context of Invention in the Ancient World". Technology and Culture Volume 44, Number 1, January 2003 (PDF). Retrieved 2007-07-23.
- ↑ Rorres, Chris. "Archimedes screw – Optimal Design". Courant Institute of Mathematical Sciences. Retrieved 2007-07-23.
- ↑ An animation of an Archimedes screw
- ↑ "SS Archimedes". wrecksite.eu. Retrieved 2011-01-22.
- ↑ Rorres, Chris. "Archimedes' Claw – Illustrations and Animations – a range of possible designs for the claw". Courant Institute of Mathematical Sciences. Retrieved 2007-07-23.
- ↑ Carroll, Bradley W. "Archimedes' Claw – watch an animation". Weber State University. Retrieved 2007-08-12.
- ↑ Hippias, 2 (cf. Galen, On temperaments 3.2, who mentions pyreia, "torches"); Anthemius of Tralles, On miraculous engines 153 [Westerman].
- ↑ John Wesley. "A Compendium of Natural Philosophy (1810) Chapter XII, Burning Glasses". Online text at Wesley Center for Applied Theology. Archived from the original on 2007-10-12. Retrieved 2007-09-14.
- ↑ "Archimedes' Weapon" Archived 2011년 2월 4일 - 웨이백 머신. Time Magazine. November 26, 1973. Retrieved 2007-08-12.
- ↑ “The Complete MythBusters Show Guide”. 2008년 11월 9일에 원본 문서에서 보존된 문서. 2011년 10월 13일에 확인함.
- ↑ Bonsor, Kevin. "How Wildfires Work". HowStuffWorks. Retrieved 2007-07-23.
- ↑ Fuels and Chemicals – Auto Ignition Temperatures
- ↑ Rorres, Chris. "The Law of the Lever According to Archimedes" Archived 2013년 9월 27일 - 웨이백 머신. Courant Institute of Mathematical Sciences. Retrieved 2010-03-20.
- ↑ Clagett, Marshall (2001). Greek Science in Antiquity. Dover Publications. ISBN 978-0-486-41973-2. Retrieved 2010-03-20.
- ↑ Quoted by Pappus of Alexandria in Synagoge, Book VIII
- ↑ Dougherty, F. C.; Macari, J.; Okamoto, C.. "Pulleys"{{ Archived 2007년 7월 18일 - 웨이백 머신. Society of Women Engineers. Retrieved 2007-07-23.
- ↑ "Ancient Greek Scientists: Hero of Alexandria" Archived 2007년 9월 5일 - 웨이백 머신. Technology Museum of Thessaloniki. Retrieved 2007-09-14.
- ↑ Cicero. "De re publica 1.xiv §21". thelatinlibrary.com. Retrieved 2007-07-23.
- ↑ Cicero. "De re publica Complete e-text in English from Gutenberg.org". Project Gutenberg. Retrieved 2007-09-18.
- ↑ “"The Antikythera Mechanism Research Project"”. 2011년 2월 21일에 원본 문서에서 보존된 문서. 2011년 2월 1일에 확인함.
- ↑ Rorres, Chris. "Spheres and Planetaria". Courant Institute of Mathematical Sciences. Retrieved 2007-07-23.
- ↑ "Ancient Moon 'computer' revisited". BBC News. November 29, 2006. Retrieved 2007-07-23.
- ↑ Plutarch. "Extract from Parallel Lives". fulltextarchive.com. Retrieved 2009-08-10.
- ↑ 나숙자, 친절한 도형 교과서, 부키, 2007, ISBN 89-6051-016-5, 243쪽
- ↑ Kaye, R.W.. "Archimedean ordered fields" Archived 2009년 3월 16일 - 웨이백 머신. web.mat.bham.ac.uk. Retrieved 2009-11-07.
- ↑ Quoted in Heath, T. L. Works of Archimedes, Dover Publications, ISBN 0-486-42084-1
- ↑ "Proof without Words: 1⁄4 + (1⁄4)2 + (1⁄4)3 + · · · = 1⁄3"
- ↑ Carroll, Bradley W. "The Sand Reckoner". Weber State University. Retrieved 2007-07-23.
- ↑ Encyclopedia of ancient Greece By Wilson, Nigel Guy p. 77 ISBN 0-7945-0225-3 (2006)
- ↑ "Editions of Archimedes' Work" Archived 2007년 8월 8일 - 웨이백 머신. Brown University Library. Retrieved 2007-07-23.
- ↑ 줄리언 해빌, 고종숙 역, 오일러 상수 감마, 승산, 2008년, ISBN 978-89-6139-018-7 , 154쪽
- ↑ The Cattle Problem
내용주[편집]
- ↑ εὕρηκα는 영어식 발음 유레카로 널리 알려져 있으나 원래의 발음은 [heurēka, 에우레카]이다. - Wiktionary:eureka
- ↑ 같은 실험을 한 동영상 - Deathray MBusters
- ↑ 셔먼 스타인은 조지 워싱턴의 유명한 일화인 벗나무와 도끼 이야기처럼 후대에 아르키메데스의 업적을 과장하기 위해 거울 무기 이야기가 만들어졌다고 본다.
- ↑ 원주율 의 실제 값은 무리수로 소수점 6자리까지 표현하면 3.141592…가 된다.
외부 링크[편집]
 위키미디어 공용에 아르키메데스 관련 미디어 분류가 있습니다.
위키미디어 공용에 아르키메데스 관련 미디어 분류가 있습니다.- O’Connor, John J.; Robertson, Edmund F. (1999년 1월). “Archimedes of Syracuse”. 《MacTutor History of Mathematics Archive》 (영어). 세인트앤드루스 대학교.
- (영어) The Archimedes Palimpsest project at The Walters Art Museum in Baltimore, Maryland
- (영어) The Mathematical Achievements and Methodologies of Archimedes
- (영어) Article examining how Archimedes may have calculated the square root of 3 at MathPages
- (영어) Archimedes On Spheres and Cylinders at MathPages
- (영어) Testing the Archimedes steam cannon Archived 2010년 3월 29일 - 웨이백 머신
















