포물선

포물선(抛物線, 문화어: 팔매선, 영어: parabola)은 이차 곡선의 일종으로, 평면상의 한 직선과 하나의 정점에 이르는 거리가 같은 점들의 집합(자취)이다. 이 때 직선을 준선, 정점을 초점이라고 한다. 그리고 어떤 포물선에 대하여 그 포물선의 준선에 수직이고 그 포물선의 초점을 지나는 직선을 그 포물선의 축이라고 하는데 그 포물선의 축은 그 포물선을 대칭시키는 유일한 직선이다. 또 어떤 포물선에 대하여 그 포물선과 그 포물선의 축의 교점을 그 포물선의 꼭짓점이라고 하는데 그 포물선의 꼭짓점은 그 포물선의 초점과 가장 가까운 그 포물선 위의 유일한 점이다. 다시 말해 어떤 포물선에 대하여 그 포물선의 초점을 중심으로 하고 그 포물선의 초점과 그 포물선의 꼭짓점을 양끝점으로 하는 선분을 반지름으로 하는 원과 그 포물선의 교점은 그 포물선의 꼭짓점으로 유일하다.
좌표평면에서의 포물선[편집]

초점의 좌표가 이고 준선의 방정식이 인 포물선의 방정식은 이고 초점의 좌표가 이고 준선의 방정식이 인 포물선의 방정식은 이다.
이는 두 점 사이의 거리 공식을 이용하여 증명할 수 있다.
다음은 "초점의 좌표가 이고 준선의 방정식이 인 포물선의 방정식은 이다."라는 명제의 증명이다.
초점의 좌표가 이고 준선의 방정식이 인 포물선 위의 점의 좌표를 라고 하자.
그러면 두 점 사이의 거리 공식에 의하여 점 에서 점 , 직선 에 이르는 거리가 각각 , 이므로
포물선의 정의에 의하여 점 의 자취의 방정식은 인데
, 이므로
점 의 자취의 방정식은 이다. 따라서 초점의 좌표가 이고 준선의 방정식이 인 포물선의 방정식은 이다.
"초점의 좌표가 이고 준선의 방정식이 인 포물선의 방정식은 이다."라는 명제도 위의 증명과 같은 방법으로 증명할 수 있다.
또 이를 통해 이차함수의 그래프는 준선이 x 또는 y축에 평행한 포물선을 그린다는 것을 알 수 있다.
역사[편집]

원뿔 곡선의 엄밀한 정의는 메나이크모스에 의해 정립되었다. 메나이크모스는 정육면체의 부피를 두배로 늘리는 문제[주해 1], 즉 의 해를 구하는 과정에서 원뿔 곡선을 그림과 같이 마주보는 두 개의 원뿔을 하나의 평면으로 자를 때 나타나는 자취로 파악하였다.[1][주해 2]
원뿔 곡선의 수학적 특성을 집대성한 것은 페르게의 아폴로니오스로 그는 모두 8권의 《원뿔 곡선론》을 저술하였다. 이 가운데 일곱권이 오늘날까지 전해지는데 네 권은 그리스어로 세 권은 아랍어로 된 판본이 남아있다.[2]
아르키메데스는 실진법을 이용하여 포물선과 직선으로 둘러싸인 도형의 넓이는 그에 내접하는 삼각형의 넓이의 4⁄3임을 증명하였다.[3] 아르키메데스의 증명 과정을 간략히 소개하면,
- 포물선을 가로지르는 직선을 한 변으로 하는 내접 삼각형을 그린다.
- 위와 같이 하여 그린 내접 삼각형에 의해 포물선은 두 구간으로 분할되며 여기에 다시 같은 방법으로 내접 삼각형을 그릴 수 있다.
- 이렇게 계속하여 내접 삼각형을 그려나가면 아래의 그림과 같이 포물선을 가로지르는 직선에 둘러싸인 도형은 무수히 많은 삼각형으로 분할된다.
- 최초의 내접 삼각형 넓이를 1이라고 하면 전체 삼각형의 넓이는 다음의 공식에 의해 구할 수 있다.
이는 공비가 1⁄4인 기하급수를 구하는 것과 같다.

17세기 이후 포물선은 다시 활발하게 응용되기 시작했는데, 고전역학의 등가속도운동의 계산[4]이나 반사망원경과 같은 광학 도구의 제작에 필수적이기 때문이다.[5] 1604년 경 갈릴레이는 탑 꼭대기에서 수평으로 발사된 물체가 단지 중력에 의해서만 영향을 받는 다면 포물선의 궤적을 그릴 것이란 것을 발견했다.[6] 뉴턴은 포물선의 미분을 연구하다 포물선 회전체 모양의 거울에서는 모든 빛이 초점으로 모인다는 것을 증명하고 이를 바탕으로 반사망원경을 만들었다. 토목공학에서 흙댐의 침윤선을 작도할 때도 사용된다.[7]
포물선의 방정식[편집]

개요에서 나타낸 바와 같이 준선이 x축에 평행하고 꼭지점이 원점에 놓인 포물선의 초점을 F(0,p)라고 하면, 이 포물선의 방정식은
- --- ⓐ
로 나타낼 수 있다. 이를 x축으로 h만큼, y축으로 k만큼 평행 이동하면
- --- ⓑ
가 된다.[8]
이때 초점과 준선 역시 평행이동 되므로 초점은 , 준선은 가 된다.
위의 식 ⓑ를 풀어
의 꼴로 나타낼 때, 라고 하면, 포물선의 방정식은
- --- ⓒ
로 나타낼 수 있다.
준선이 y축에 평행하다면 식 ⓑ는 x와 y가 뒤바뀌어 꼴이 될 것이다.[8]
접선의 방정식[편집]

포물선 위의 한 점에서 만나는 접선의 기울기는 포물선의 방정식을 미분하여 구할 수 있다.[9]
예를 들어 위의 한 점 와 만나는 접선의 기울기를 계산하면,
이므로, 일 때 기울기는 2가 된다. 따라서 이 직선의 방정식은 의 꼴임을 알 수 있다. 한편, 이 직선이 점 를 지나므로 c는 -1 이 된다. 따라서 위의 한 점 와 만나는 직선의 방정식은 이 된다. 포물선 위의 한 점에서 만나는 접선은 유일하고, 역으로 특정한 기울기를 갖는 접선은 오직 포물선 위의 한 점에서만 만난다.
기울기가 주어졌을 경우[편집]
기울기가 로 주어졌을 경우, 포물선의 접선의 방정식은 다음과 같이 구할 수 있다.
- 일 때
- 일 때
접점이 주어졌을 경우[편집]
포물선 위의 점 에서 접선을 그었을 경우, 포물선의 접선의 방정식은 다음과 같이 구할 수 있다.
- 일 때
- 일 때
포물선의 극방정식[편집]
극좌표계에서 포물선은 다음과 같이 정의된다.
성질[편집]
원뿔곡선[편집]
포물선은 원뿔곡선의 하나이다. 원뿔곡선의 일반적인 방정식은
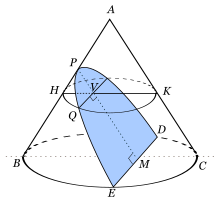
으로 나타낼 수 있고, 위 식에서 의 관계가 성립할 때 포물선이 된다.[10] 원뿔곡선에서 포물선이 갖는 성질을 기하학적으로 살펴보면 그림과 같이 하나의 평면으로 원뿔을 중심각과 나란한 방향으로 절단할 때 포물선이 나타나게 된다.
포물선의 합동[편집]

어떤 포물선에 대하여 그 포물선의 준선에 평행하고 그 초점을 지나는 직선과 그 포물선의 두 교점을 양 끝점으로 하는 선분을 그 포물선의 통경이라고 한다. 일반적인 포물선의 방정식
에서 살펴 보면 통경의 양 끝 점의 x축 성분은 로 놓아 구할 수 있다.
와 같이 되어 통경의 두 끝점 좌표는 가 되고, 선분의 길이는 임을 알 수 있다. 즉 통경의 길이는 언제나 꼭지점과 초점 사이의 거리의 4배이다.[11] 이와 같이 통경의 길이는 각 포물선의 방정식 마다 유일하고 통경의 길이가 같다면 두 포물선은 합동이다.[12]
반사성질[편집]

그림과 같이 포물선 위의 한 점 E에서 만나는 접선을 생각하면 포물선으로 들어오는 빛의 입사각과 접선에서 초점으로 나가는 반사각이 같음을 알 수 있다. 이와 같은 포물선의 성질은 여러 곳에서 응용되고 있다. 포물선을 회전하여 반사면을 만들면 빛과 같은 전자기파를 초점으로 모을 수도 있고, 반대로 초점에 광원을 놓으면 빛은 포물면에 반사된 뒤 곧게 나아간다. 이러한 반사 성질은 반사망원경이나 파라볼라 안테나, 손전등과 같은 것에 사용된다.[5]
-
팔로마천문대의 헤일 반사망원경
-
반사되어 나가는 손전등의 빛
같이 보기[편집]
각주[편집]
내용주[편집]
- ↑ 정육면체의 부피 문제는 고대 그리시 시대 기하학의 난제 가운데 하나였다. 이와 관련해서는 미노스의 묘비에 얽힌 전설, 아폴로의 제단에 얽힌 전설 등 다양한 이야기가 전해지고 있다. - Howard Eve, 이우영 신향균 역, 《수학사》, 경문사, ISBN 89-7282-298-1, 95-96쪽
- ↑ 메나이크모스의 해는 전하지 않는다. 11세기 페르시아의 수학자 오마르 하이얌이 포물선과 원을 이용하여 꼴의 삼차방정식에 대한 양의 실수근을 작도하였다. - 스티븐 크란츠, 남호영 장영호 역, 《문제해결로 살펴본 수학사》, 경문사, ISBN 978-89-6105-603-8, 88-89쪽
참조주[편집]
- ↑ 토비아스 단치히, 심재관 역, 《과학의 언어 수》, 지식의숲, 2007년, ISBN 978-89-9176-244-2, 366쪽
- ↑ Howard Eve, 이우영 신향균 역, 《수학사》, 경문사, ISBN 89-7282-298-1, 156-157 쪽
- ↑ Stein, Sherman (2006). 《아르키메데스》. 번역 이우영. 경문사. 87쪽. ISBN 89-7282-926-9.
- ↑ 오가미 마사시, 임정 역, 《수학으로 풀어보는 물리의 법칙》, 이지북, 2005년, ISBN 978-89-5624-190-6, 137-138쪽
- ↑ 가 나 George F. Simmons, 고석구 외 역, 《미적분학과 해석기하》, 경문사, ISBN 89-7282-435-6, 616쪽
- ↑ 스티브 크란츠, 남호영 장영호 역, 《문제해결로 살펴본 수학사》, 경문사, ISBN 978-89-6105-603-8, 612쪽
- ↑ 장병욱; 전우정; 송창섭; 유찬; 임성훈; 김용성 (2010). 《토질역학》. 구미서관. 109쪽. ISBN 978-89-8225-697-4.
- ↑ 가 나 스티브 크란츠, 남호영 장영호 역, 《문제해결로 살펴본 수학사》, 경문사, ISBN 978-89-6105-603-8, 69쪽 - 이 책에서는 초점을 원점에 놓은 포물선을 평행이동 시켜 일반적인 관계식을 구한다. 그러나 그 결과는 본질적으로 같다.
- ↑ 고바야시 미치마사, 조윤동 역, 《문과 학생을 위한 미적분》, 아카데미, ISBN 978-89-7616-425-4, 85-92쪽
- ↑ Methods to solve Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0
- ↑ latus rectum
- ↑ “Lesson 34: Are All Parabolas Congruent?” (PDF). 2016년 5월 9일에 원본 문서 (PDF)에서 보존된 문서. 2016년 4월 24일에 확인함.
외부 링크[편집]
- “Parabola”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4.
- Weisstein, Eric Wolfgang. “Parabola”. 《Wolfram MathWorld》 (영어). Wolfram Research.



















































