쌍곡선 쌍곡선 (雙曲線, 영어 : hyperbola )은 평면 위에 있는 두 정점으로부터의 거리의 차가 일정한 점들의 집합으로 만들어지는 곡선을 말한다. 이때 기준이 되는 두 정점을 초점 이라 한다.
한초점이 극히 멀어질수록 쌍곡선은 포물선 에 가까워진다. 한편 쌍곡선은 초점에서 멀어질수록 점근선 이라고 불리는 직선 에 가까워지며, 쌍곡선의 점근선 은 두 개가 있다.
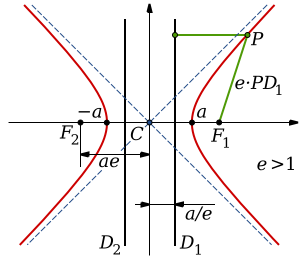
직교 좌표계상의 성질 [ 편집 ] 쌍곡선은 두 개의 빨간색으로 나타낸 곡선을 말한다. 파란 점선으로 그려진 직선을 쌍곡선의 점근선(asymptotes)이라하며, 두 점근선은 쌍곡선의 중심 “C”에서 만난다. 두 초점은 각각 F 1 과 F 2 로 표시하였고, 이 두 초점을 연결하는 얇은 검은색 직선을 횡단축(traverse axis)이라 한다. 횡단축과 수직이며 쌍곡선의 중심을 지나는 검은색 얇은 직선을 켤레축(conjugate axis)이라 한다. 켤레축에 나란한(횡단축에 수직인) 두 개의 검은색 두꺼운 직선을 주선(directrices)라고 하며, 각각 D 1 과 D 2 로 표시되었다. 이심율(eccentricity) e 는 쌍곡선 위의 한 점 P 로부터, 한 초점까지의 거리와 주선까지의 거리의 비(녹색선 참고)와 같다. 두 꼭짓점은 각각 횡단축의 중심으로부터 ±’’a’’ 만큼 떨어져 있다. 다음은 변수들에 대한 설명이다:a — 중심 ‘’C’’로부터 꼭짓점 까지의 거리 b — 꼭짓점에서 횡단축에 수직하게 점근선까지 그은 선분의 길이c — 중심 ‘’C’’에서 초점, F 1 또는 F 2 까지의 거리 초점이
x
{\displaystyle x}
직교 좌표계 로 표현하면 다음과 같은 식이 된다.
x
2
a
2
−
y
2
b
2
=
1
{\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}
여기서
a
,
b
{\displaystyle a,b}
c
=
a
2
+
b
2
{\displaystyle \textstyle c={\sqrt {a^{2}+b^{2}}}}
(
−
c
,
0
)
,
(
c
,
0
)
{\displaystyle (-c,0),(c,0)}
쌍곡선의 이심률 (Eccentricity)은 다음과 같이 정의된다.
c
a
=
a
2
+
b
2
a
{\displaystyle {\frac {c}{a}}={\frac {\sqrt {a^{2}+b^{2}}}{a}}}
쌍곡선의 점근선은 다음과 같게 된다.
y
=
±
b
a
x
{\displaystyle y=\pm {\frac {b}{a}}x}
즉, 두 개의 직선이 된다.
이와 별도로, 두 축을 점근선으로 하는 쌍곡선은 다음과 같은 식으로 표현가능하다.
x
y
=
k
{\displaystyle xy=k}
이 때,
k
{\displaystyle k}
쌍곡선과 이차 방정식 [ 편집 ] 쌍곡선은 직교좌표계에서 이차방정식
A
x
x
x
2
+
2
A
x
y
x
y
+
A
y
y
y
2
+
2
B
x
x
+
2
B
y
y
+
C
=
0
{\displaystyle A_{xx}x^{2}+2A_{xy}xy+A_{yy}y^{2}+2B_{x}x+2B_{y}y+C=0}
을 이용하여 정의할 수도 있다. 위의 이차 방정식의 계수
A xx A xy A yy B x B y C 가
D
=
|
A
x
x
A
x
y
A
x
y
A
y
y
|
<
0
{\displaystyle D={\begin{vmatrix}A_{xx}&A_{xy}\\A_{xy}&A_{yy}\end{vmatrix}}<0\,}
를 만족하면 위의 이차방정식은 쌍곡선을 나타낸다. 쌍곡선의 특별한 형태로 “퇴화 쌍곡선(degenerate hyperbola)를 들 수 있다.
퇴화 쌍곡선은 교차하는 두 직선으로 이루어지며, 위의 이차방정식의 계수를 원으로 하는 아래의 행렬식이
Δ
:=
|
A
x
x
A
x
y
B
x
A
x
y
A
y
y
B
y
B
x
B
y
C
|
=
0
{\displaystyle \Delta :={\begin{vmatrix}A_{xx}&A_{xy}&B_{x}\\A_{xy}&A_{yy}&B_{y}\\B_{x}&B_{y}&C\end{vmatrix}}=0}
을 만족하면 위의 이차 방정식은 퇴화 쌍곡선을 나타낸다.
위의 행렬식 Δ를 원뿔곡선의 판별식 이라 부르기도 한다.[1]
쌍곡선의 중심 (x c y c
x
c
=
−
1
D
|
B
x
A
x
y
B
y
A
y
y
|
{\displaystyle x_{c}=-{\frac {1}{D}}{\begin{vmatrix}B_{x}&A_{xy}\\B_{y}&A_{yy}\end{vmatrix}}}
y
c
=
−
1
D
|
A
x
x
B
x
A
x
y
B
y
|
{\displaystyle y_{c}=-{\frac {1}{D}}{\begin{vmatrix}A_{xx}&B_{x}\\A_{xy}&B_{y}\end{vmatrix}}}
에 의해 구할 수 있다.
쌍곡선의 중심이 원점이 되도록 평행이동하여 얻은 새로운 좌표계, ξ = x − x c and η = y − y c 를 이용하여 쌍곡선의 방정식은
A
x
x
ξ
2
+
2
A
x
y
ξ
η
+
A
y
y
η
2
+
Δ
D
=
0
{\displaystyle A_{xx}\xi ^{2}+2A_{xy}\xi \eta +A_{yy}\eta ^{2}+{\frac {\Delta }{D}}=0}
로 쓸 수 있다. 쌍곡선의 주축은 양의 ‘’x’’-축과 Φ의 각을 이룬다. 여기서 Φ는 다음과 같이 구할 수 있다.
tan
2
Φ
=
2
A
x
y
A
x
x
−
A
y
y
{\displaystyle \tan 2\Phi ={\frac {2A_{xy}}{A_{xx}-A_{yy}}}}
좌표축을 회전하여 ‘’x’’-축이 횡단축과 일치하도록 하면 앞의 이차방정식은 쌍곡선의 표준형 방정식
x
2
a
2
−
y
2
b
2
=
1
{\displaystyle {\frac {{x}^{2}}{a^{2}}}-{\frac {{y}^{2}}{b^{2}}}=1}
으로 바꿀 수 있다.
기하학적 성질 [ 편집 ] 쌍곡선 위의 모든 점은 두 초점과의 거리의 차가 일정하다. 다음은 직교 좌표계에서 어렵지 않게 증명가능하다.
쌍곡선 위의 모든 점은 두 초점과의 거리의 차가 일정하다.
한 초점에서 나온 빛은 쌍곡선에 반사되면 다른 초점에서 나온 빛처럼 보인다.
쌍곡선 위의 점에서 점근선에 수선의 발을 내리면 그 길이의 곱은 일정하다.
쌍곡선 위의 한 점을 지나며 두 점근선에 평행한 두 개의 직선과 두 점근선으로 이루어진 평행사변형의 면적은 일정하다.
초점이 일치하는 쌍곡선과 타원 은 교점에서 각각의 접선이 수직이다. 접선의 방정식 [ 편집 ] 쌍곡선
x
2
a
2
−
y
2
b
2
=
1
{\displaystyle \textstyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}
(
x
1
,
y
1
)
{\displaystyle (x_{1},y_{1})}
x
x
1
a
2
−
y
y
1
b
2
=
1
{\displaystyle {\frac {xx_{1}}{a^{2}}}-{\frac {yy_{1}}{b^{2}}}=1}
또한, 기울기
m
{\displaystyle m}
y
=
m
x
±
a
2
m
2
−
b
2
{\displaystyle y=mx\pm {\sqrt {a^{2}m^{2}-b^{2}}}}
↑ Korn, Granino A. and Korn, Theresa M. Mathematical Handbook for Scientists and Engineers: Definitions, Theorems, and Formulas for Reference and Review , Dover Publ., second edition, 2000: p. 40.