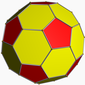
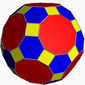
아르키메데스의 다면체
아르키메데스의 다면체는 두 종류 이상의 정다각형으로 이루어져 있으며, 각 꼭짓점에 모인 면이 배치가 서로 같은 볼록 다면체로, 각기둥과 엇각기둥을 제외한 다면체이다. 두 개의 동일한 아르키메데스의 다면체가 있다고 할 때, 한 아르키메데스의 다면체의 한 꼭짓점과 다른 아르키메데스의 다면체의 다른 꼭짓점을 일치시키면 도형의 다른 부분들이 완전히 일치해야 한다. 이 조건은 존슨의 다면체중 늘린 비틀어 붙인 두 사각지붕과 아르키메데스의 다면체 중 마름모육팔면체의 차이점을 보여준다. 한 종류의 다각형으로 이루어진 정다면체와 다르고, 또한 각 꼭짓점의 모양이 다른 존슨의 다면체와도 차이가 있다. 각 꼭짓점 배치가 같으면서 두 가지 이상의 정다각형으로 된 타일링은 아르키메데스 타일링이라고 한다. 이들은 모두 정다면체/준정다면체에 작업을 해서 얻을 수 있다. 깎기, 절반 깎기, 쌍대깎기, 부풀리기(준정다면체 절반깎기라고도 함), 부풀려 깎기, 다듬기로 총 6가지가 있다.
고대 그리스 시대의 수학자 아르키메데스가 발견하였지만 그 결과는 잊혀졌다. 르네상스 시기에 와서 1619년 요하네스 케플러가 재발견했다. 케플러는 볼록하지 않은 모양도 찾았는데, 이 도형은 케플러-푸앵소 다면체라고 부른다. 한마디로 아르키메데스의 다면체는 일명 준정다면체라고 할 수 있다.
종류[편집]
13 종류(대칭인 모양을 따로 세면 15 종류)의 다면체가 있다. 그리고 타일링에도 적용시킨다면 7개가 더 있어서 총 20개 있다. 단, 각기둥이나 엇각기둥, 늘린 삼각형 타일링 (또는 비틀어 늘린 사각형 타일링) 은 점추이더라도 아르키메데스의 다면체/타일링으로 보지 않는다. 이들 중에서 깎은 정다면체와 깎은 정다각형 타일링가 7개, 준정다면체와 준정다각형 타일링은 3개이고, 깎은 준정다면체와 깎은 준정다각형 타일링이 3개, 부풀리고 다듬은 정다면체 및 부풀려 다듬은 정다각형 타일링이 각각 3개와 4개 있다.
| 이름 | 꼭짓점 구성 | 대칭군 | 도형 구성 | 모서리 수 | 꼭짓점 수 | ||
|---|---|---|---|---|---|---|---|
| 육팔면체 | 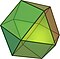 (동영상) |
14 | 8 삼각형 6 사각형 |
24 | 12 | 3,4,3,4 | Oh |
| 십이이십면체 | 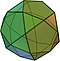 (동영상) |
32 | 20 삼각형 12 오각형 |
60 | 30 | 3,5,3,5 | Ih |
| 깎은 정사면체 |  (동영상) |
8 | 4 삼각형 4 육각형 |
18 | 12 | 3,6,6 | Td |
| 깎은 정육면체 |  (동영상) |
14 | 8 삼각형 6 팔각형 |
36 | 24 | 3,8,8 | Oh |
| 깎은 정팔면체 |  (동영상) |
14 | 6 사각형 8 육각형 |
36 | 24 | 4,6,6 | Oh |
| 깎은 정십이면체 | 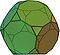 (동영상) |
32 | 20 삼각형 12 십각형 |
90 | 60 | 3,10,10 | Ih |
| 깎은 정이십면체 |  (동영상) |
32 | 12 오각형 20 육각형 |
90 | 60 | 5,6,6 | Ih |
| 마름모육팔면체 | 부풀린 육팔면체 (동영상) |
26 | 8 삼각형 18 사각형 |
48 | 24 | 3,4,4,4 | Oh |
| 깎은 육팔면체 |  (동영상) |
26 | 12 사각형 8 육각형 6 팔각형 |
72 | 48 | 4,6,8 | Oh |
| 마름모십이이십면체 | 부풀린 십이이십면체 (동영상) |
62 | 20 삼각형 30 사각형 12 오각형 |
120 | 60 | 3,4,5,4 | Ih |
| 깎은 십이이십면체 |  (동영상) |
62 | 30 사각형 20 육각형 12 십각형 |
180 | 120 | 4,6,10 | Ih |
| 다듬은 정육면체 (다듬은 육팔면체) (2 대칭형) |
 (동영상)  (동영상) |
38 | 32 삼각형 6 사각형 |
60 | 24 | 3,3,3,3,4 | O |
| 다듬은 정십이면체 (다듬은 십이이십면체) (2 대칭형) |
 (동영상)  (동영상) |
92 | 80 삼각형 12 오각형 |
150 | 60 | 3,3,3,3,5 | I |