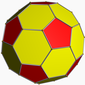
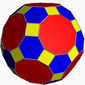
깎은 정이십면체

깎은 정이십면체
(클릭해서 회전하는 모델을 볼 수 있다)
종류	아르키메데스의 다면체 고른 다면체
성분	F = 32, E = 90, V = 60 (χ = 2)
면의 수{변의 수}	12{5}+20{6}
콘웨이 표기법	tI
슐레플리 기호	t{3,5}
	t0,1{3,5}
위토프 기호	2 5 | 3
콕서터 다이어그램
대칭군	Ih, H3, [5,3], (*532), 120차
회전군	I, [5,3]+, (532), 60차
이면각	6-6: 138.189685° 6-5: 142.62°
참조	U25, C27, W9
특성	반정다면체 볼록
색칠된 면	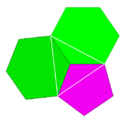5.6.6 (꼭짓점 도형)
오방십이면체 (쌍대다면체)	전개도

깎은 정이십면체는 정이십면체의 각 꼭짓점(모서리의 삼등분점)을 잘라내어 만든 다면체이다. 텔스타 축구공의 모양이며, 이 때문에 이 다면체는 축구공의 대명사가 되었다. 면의 수는 깎은 정십이면체와 같이 32개, 모서리의 수는 90개, 꼭짓점의 수는 60개이다. 깎인 정삼각형 면은 깎은 정사면체, 깎은 정팔면체와 같이 정육각형인 면이 생기고 깎인 꼭짓점은 모두 정오각형인 면이 생기게 된다.

특징

• 탄소원자 60개가 결합하여 이루어진 풀러렌의 구조이다.
• 정십이면체와 모습과 이름이 유사해 혼동하는 경우가 있으나, 깎은 정이십면체는 정다면체가 아닌 일반적인 다면체에 속한다.

겉넓이와 부피

한 모서리의 길이가 a인 깎은 정이십면체의 겉넓이 A와 부피 V는 다음과 같다.

${\begin{aligned}A&=3\left(10{\sqrt {3}}+{\sqrt {5}}{\sqrt {5+2{\sqrt {5}}}}\right)a^{2}\approx 72.607253a^{2}\\V&={\frac {1}{4}}(125+43{\sqrt {5}})a^{3}\approx 55.287731a^{3}.\\\end{aligned}}$

비슷한 다면체

정십이면체

깎은 정십이면체

십이이십면체

깎은 정이십면체

정이십면체