엇각기둥
| 고른 엇각기둥의 집합 | |
|---|---|
 | |
| 종류 | 고른 다면체 |
| 면 | n각형 2개, 삼각형 2n개 |
| 모서리 | 4n |
| 꼭짓점 | 2n |
| 콘웨이 다면체 표기법 | An |
| 꼭짓점 배치 | 3.3.3.n |
| 슐레플리 기호 | s{2,2n} sr{2,n} { } ⊗ {n} |
| 콕서터 다이어그램 | |
| 대칭군 | Dnd, [2+,2n], (2*n), 4n차 |
| 회전군 | Dn, [2,n]+, (22n), 2n차 |
| 쌍대다면체 | 엇각쌍뿔 |
| 특성 | 볼록, 점추이 반정다면체 |
| 전개도 | 
|
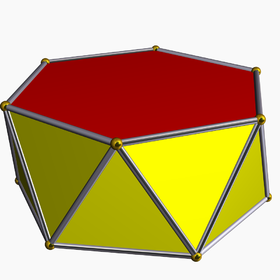
기하학에서, n각의 엇각기둥은 평행하고 동일한 n각형 두 개를 교대로 이루어진 삼각형의 띠로 연결된 다면체이다. 엇각기둥은 기둥다면체의 부분이고 (퇴화된 종류의) 다듬은 다면체이다.
엇각기둥은 밑면이 서로 꼬여있다는 것과 옆면이 사각형이 아니라 삼각형인 것을 제외하고는 각기둥과 동일하다.
정 n각형 밑면의 경우에는, 보통은 복사본이 180°n도만큼 뒤틀린 경우로 생각한다. 추가 정규성은 밑면의 중심을 잇는 선이 밑면과 수직일 때 얻어지고, 그러면 이 각기둥은 직엇각기둥이 된다. 면에 대해서는, n각형의 밑면 2개와 그 둘을 연결하는 2n개의 이등변 삼각형이 있다.
고른 엇각기둥[편집]
고른 엇각기둥은 밑면을 제외하고 정삼각형 2n개를 면으로 가진다. 그룹에서는 고른 각기둥처럼 고른 엇각기둥은 무한한 점추이 고른 다면체의 급수를 만든다. n = 2일 때, 퇴화된 경우로 정사면체를 엇이각기둥으로 보고, n = 3일 때는 정상적인 정팔면체를 엇삼각기둥으로 본다.
엇각기둥의 쌍대다면체는 엇각쌍뿔이다. 이것의 존재성은 요하네스 케플러에 의해 토론되었으며 이름도 마찬가지로 케플러에 의해 지어졌고, 이전에 아르키메데스가 아르키메데스 다면체와 같은 꼭짓점 조건을 만족시키는 것으로 알려져있었을 가능성도 있다.
| 고른 엇각기둥족 n.3.3.3 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 다면체 | ||||||||||||
| 타일링 | ||||||||||||
| 배치 | V2.3.3.3 | 3.3.3.3 | 4.3.3.3 | 5.3.3.3 | 6.3.3.3 | 7.3.3.3 | 8.3.3.3 | 9.3.3.3 | 10.3.3.3 | 11.3.3.3 | 12.3.3.3 | ...∞.3.3.3 |
슈미겔 다이어그램[편집]
 A3 |
 A4 |
 A5 |
 A6 |
 A7 |
 A8 |
직교 좌표[편집]
n각영 밑면과 이등변삼각형을 가지는 직엇각기둥의 꼭짓점의 직교 좌표는 다음과 같다:
k는 0에서 2n − 1까지의 정수이다; 삼각형이 정삼각형일 경우에는 다음과 같다:
관련 다면체[편집]
낮은 대칭 형태의 깎은 정팔면체(깎은 엇삼각기둥)를 포함하는 무한한 깎은 엇각기둥의 집합이 존재한다. 이것들은 다듬은 엇각기둥을 만들기 위해서 교대될 수 있다. 깎은 엇각기둥 중 둘은 존슨의 다면체이고, 다듬은 엇삼각기둥은 낮은 대칭의 정이십면체이다.
| 엇각기둥 | ||||
|---|---|---|---|---|

|

|

|

|
... |
| s{2,4} | s{2,6} | s{2,8} | s{2,10} | s{2,2n} |
| 깎은 엇각기둥 | ||||

|

|

|

|
... |
| ts{2,4} | ts{2,6} | ts{2,8} | ts{2,10} | ts{2,2n} |
| 다듬은 엇각기둥 | ||||
| J84 | 정이십면체 | J85 | 불규칙... | |

|

|

|

|
... |
| ss{2,4} | ss{2,6} | ss{2,8} | ss{2,10} | ss{2,2n} |
대칭[편집]
밑면이 정n각형이고 옆면이 이등변삼각형인 직 엇각기둥의 대칭군은 4n차 Dnd이나, 정사면체의 경우에는 D2d의 세 형태를 부분군으로 가지는 더 큰 24차 대칭군 Td을 가지고, 정팔면체는 D3d의 네 형태를 부분군으로 가지는 더 큰 48차 대칭군 Oh을 가진다.
회전군은 2n차 Dn이고, 정사면체의 경우는 D2의 세 형태를 부분군으로 가지는더 큰 12차 회전군 T를 가지고, 정팔면체는 D3의 네 형태를 부분군으로 가지는 더 큰 24차 회전군 O를 가진다.
별모양 엇각기둥[편집]
 5/2-엇각기둥 |
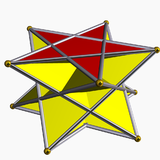 5/3-엇각기둥 | ||||
 9/2-엇각기둥 |
 9/4-엇각기둥 |
 9/5-엇각기둥 | |||
별모양 고른 엇각기둥은 밑면인 별 다각형 {p/q}으로 이름이 결정되고, 순방향과 역방항(교차된) 솔루션이 나온다. 교차된 형태는 교차된 꼭짓점 도형을 가지고 p/q 대신에 역방향 분수 p/(p - q)를 사용한다. 예를 들면 5/2 대신에 5/3을 쓴다.
순방향이 아닌 역방향 형태에서는, 별모양 밑변에 접하는 삼각형은 회전 대칭축과 교차한다.
별 정다각형을 밑면으로 가지는 일부 역방항 별 엇각기둥은 모서리의 길이가 같아질 수 없어서, 고른 다면체가 될 수 없다. 별 엇각기둥 결합물은 p와 q를 공통으로 가지도록 만들 수 있다; 따라서 10/4 엇각기둥은 두 5/2 별 엇각기둥의 결합이다.
| 대칭 | 별모양 | |||
|---|---|---|---|---|
| d5h [2,5] (*225) |
 3.3.3.5/2 | |||
| d5d [2+,5] (2*5) |
 3.3.3.5/3 | |||
| d7h [2,7] (*227) |
 3.3.3.7/2 |
 3.3.3.7/4 | ||
| d7d [2+,7] (2*7) |
 3.3.3.7/3 | |||
| d8d [2+,8] (2*8) |
 3.3.3.8/3 |
 3.3.3.8/5 | ||
| d9h [2,9] (*229) |
 3.3.3.9/2 |
 3.3.3.9/4 | ||
| d9d [2+,9] (2*9) |
 3.3.3.9/5 | |||
| d10d [2+,10] (2*10) |
 3.3.3.10/3 | |||
| d11h [2,11] (*2.2.11) |
 3.3.3.11/2 |
 3.3.3.11/4 |
 3.3.3.11/6 | |
| d11d [2+,11] (2*11) |
 3.3.3.11/3 |
 3.3.3.11/5 |
 3.3.3.11/7 | |
| d12d [2+,12] (2*12) |
 3.3.3.12/5 |
 3.3.3.12/7 | ||
| ... | ||||
- 각기둥
- 무한 엇각기둥
- 큰 엇각기둥 – 사차원 다포체
- 원 월드 트레이드 센터, 늘린 엇사각기둥의 형태를 가지는 건물이다[1]
같이 보기[편집]
참조[편집]
- Anthony Pugh (1976). 《Polyhedra: A visual approach》. California: University of California Press Berkeley. ISBN 0-520-03056-7. Chapter 2: Archimedean polyhedra, prisma and antiprisms
- ↑ Kabai, Sándor. “One World Trade Center Antiprism”. Wolfram Demonstrations Project. 2013년 10월 8일에 확인함.
외부 링크[편집]
- Weisstein, Eric Wolfgang. “Antiprism”. 《Wolfram MathWorld》 (영어). Wolfram Research.
- Olshevsky, George. “Antiprism”. 《Glossary for Hyperspace》. 2007년 2월 4일에 원본 문서에서 보존된 문서.
- Olshevsky, George. “Prismatic polytopes”. 《Glossary for Hyperspace》. 2007년 2월 4일에 원본 문서에서 보존된 문서.
- Nonconvex Prisms and Antiprisms
- Paper models of prisms and antiprisms


