전하

전하(電荷, 영어: electric charge)는 전자기장내에서 전기현상을 일으키는 주체적인 원인이다. 특히 공간에 있는 가상의 점이 갖는 전하를 점전하라고 하고, 전하의 양을 전하량(Q)이라고 한다.
전하의 국제단위는 쿨롱이며, 단위기호는 C이다.[1] 1 쿨롱은 매우 큰 단위이며, 약 6.25×1018개의 전자나 양성자들의 전하량이다. 반대로, 전자 또는 양성자 한 개의 전하량은 1.6021773349 ×10-19 쿨롱이며,[2] 이를 기본 전하라고 부른다.
또한, 전하는 음의 전하와 양의 전하가 있다. (이는 질량과 같이 양의 값만 있는 다른 물리량과 다르다.) 통상적으로 양성자나 양전자 따위의 전하를 양으로, 전자 등의 전하를 음으로 놓는다. 이렇게 전하를 띄는 물체는 대전체(帶電體)로 부른다.
개요[편집]
고대 그리스 시대에 이미 호박을 문지르면 옷자락이나 먼지 같은 것들이 달라붙는 다는 것이 알려져 있었다. 유럽의 언어들에서 전기를 뜻하는 단어들(영어: electricity, 프랑스어: électricité, 독일어: Elektrizität)은 호박을 뜻하는 고대 그리스어: ήλεκτρον 엘렉트론[*]에서 기원하였다. 18세기 중엽 벤저민 프랭클린은 뇌우 속으로 연을 날리는 매우 위험한 실험을 통해 번개가 호박에 의해 발생되는 것과 동일한 전기임을 입증하였다.[3]
같은 종류의 전하 사이에서는 척력이 작용하고 다른 종류의 전하 사이에서는 인력이 작용한다. 이 두 종류의 전하를 양전하와 음전하라고 한다. 물체가 양전하 또는 음전하를 띄게 되는 근본적인 이유는 기본 입자의 전하 때문이다. 전자는 음전하를 띄고 두 개의 위 쿼크와 하나의 아래 쿼크로 이루어진 양성자는 양전하를 띈다. 기본 입자를 고려하지 않는 원자 단위 이상에서 전하량은 모두 전자 한 개의 전하량인 1.6021773349 ×10-19에 대한 정수배로 존재한다. 즉, 일반적인 경우 전자 한 개가 갖는 전하량이 전하량의 최소 기준으로 사용될 수 있다.[2]
일반적으로 원자는 양성자와 전자의 수가 균형을 이루어 전기적으로 중성인 상태에 있다. 그러나, 원자의 가장 바깥 껍질에 위치한 전자는 상대적으로 약하게 결합되어 있기 때문에 마찰과 같은 물리적 힘에 의해 쉽게 원자에서 벗어나게 된다. 이렇게 한 물질에서 다른 물질로 전자들이 이동하게 되면 전자를 잃은 쪽 물질은 양전하를 띄게 되고 반대편의 물질은 음전하를 띄게 된다. 마찰과 같은 것에 의해 축적되어 흐르지 않는 전기를 정전기라고 한다. 전기가 잘 흐르지 않는 부도체가 마찰하면 정전기가 발생한다. 예를 들어 건조한 겨울철 고무나 플라스틱으로 된 밑창이 달린 신발을 신고 걷는다면 마찰로 인해 우리 몸에 정전기가 발생할 것이다. 이렇게 발생된 정전기는 자동차 문 손잡이와 같은 금속을 만나면 전기충격을 줄 수도 있다.[4]
전하에 작용하는 힘[편집]
샤를 드 쿨롱은 금속공과 비틀림 저울을 이용하여 두 점전하 사이에 작용하는 힘을 측정하고, 두 전하 사이에서 작용하는 힘은 두전하 크기의 곱에 비례하고 거리의 제곱에 반비례한다는 쿨롱의 법칙을 발견하였다.[5]
| 쿨롱의 전하 측정 시험 | |
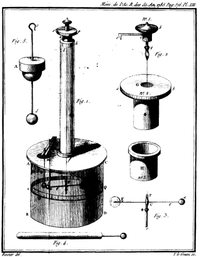 |
시험과정 1. 금박을 입힌 작은 금속공을 여러 개 준비한다. 2. 하나의 금속공을 마찰하여 정전기를 대전시킨다. 3. 대전된 금속공에 다른 금속 공을 접촉시키면 각 금속공의 전하량은 원래 전하량의 ½이 된다. 이와 같은 방법으로 마찰로 대전된 전하량에 대해 1/4, 1/8, 1/16의 전하량을 갖는 금속공을 준비한다. 4. 왼쪽 그림과 같은 비틀림 저울을 설치하고 한쪽에는 1/2 전하량을 갖는 금속공을 놓고 다른 쪽에는 서로 다른 전하량을 갖는 금속공을 연결하여 금속공이 이동하는 거리를 측정한다. |
| 시험 결과 두 전하 사이에서 작용하는 힘은 두전하 크기의 곱에 비례하고 거리의 제곱에 반비례한다. | |
위 실험 결과를 식으로 나타내면 다음과 같다.[5]
- F=힘, Ke=쿨롱 상수, q_1 · q_2=전하의 크기, r=두 전하 사이의 거리
- 위 식에서 Ke는 쿨롱 힘 상수로 이 상수의 크기는 다음과 같다.
따라서, 각각 1C의 크기를 갖는 두 전하가 1m의 거리에 있을 때 발생하는 힘은 다음과 같이 계산될 수 있다.[5]
즉, 각각 1C의 전하량을 갖는 두 점전하가 1m의 거리에 있을 때 발생하는 힘은 10t 트럭 10만 대와 맞먹는다. 이렇게 큰 힘이 기준 단위가 된 것은 전기에 대한 상세한 지식이 없는 시절에 이를 측정 단위로 삼았기 때문이다. 실제 일상 생활에서 발생하는 정전기의 전하량은 대략 ×10-6에서 ×10-9 쿨롱 정도에 불과하다.[5]
전하량[편집]
하나의 전자가 갖는 전하량은 너무 작기 때문에 실제 전하량을 측정하는 SI 단위인 쿨롱은 6.24150962915265×1018개의 전자가 한꺼번에 수송하는 전하량을 사용한다. 이 때 전류의 단위 암페어는 1초 동안 1쿨롱의 전하가 흐른 것으로 이해될 수 있다.[2][주해 1]
같이 읽기[편집]
주해[편집]
각주[편집]
- ↑ 화학용어사전, 일진사, 2006, ISBN 89-429-0903-5
- ↑ 가 나 다 장요한 외 공저, 기초회로이론, 학문사, ISBN 89-467-5054-5, 42쪽
- ↑ 찰스 테일러 외, 김동광 역, 과학의 발견, 비룡소, 2001, ISBN 89-491-5016-6, 161쪽
- ↑ 찰스 테일러 외, 김동광 역, 과학의 발견, 비룡소, 2001, ISBN 89-491-5016-6, 163쪽
- ↑ 가 나 다 라 한국물리학회, 전기와 자기의 밀고 당기기, 동아사이언스, 2006, ISBN 89-91844-09-X, 65-68쪽






