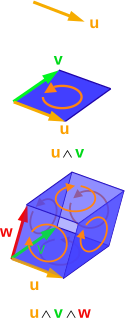
외대수의 1차 · 2차 · 3차 원소는 기하학적으로 각각 방향 을 갖춘 선분 · 평행사변형 · 평행육면체 로 해석할 수 있다. 외대수 원소의 노름 은 평행육면체의 부피와 같다. 추상대수학 과 미분기하학 에서 외대수 (外代數, 영어 : exterior algebra ) 또는 그라스만 대수 (Graßmann代數, 영어 : Grassmann algebra )는 어떤 주어진 벡터 공간 에 대하여, 그 벡터들의 완전 반대칭 조합들로 구성된 벡터 공간 및 그 위에 정의된 이항 연산 으로 구성되는 단위 결합 대수 이자 호프 대수 이다. 기하학 적으로, 이는 부호수를 갖는 넓이 또는 부피를 나타낸다.
가환환
K
{\displaystyle K}
가군
V
{\displaystyle V}
텐서 대수
T
(
V
)
=
⨁
n
=
0
∞
T
n
(
V
)
=
⨁
n
=
0
∞
V
⊗
K
V
⊗
K
⋯
⊗
K
V
⏞
n
{\displaystyle T(V)=\bigoplus _{n=0}^{\infty }T^{n}(V)=\bigoplus _{n=0}^{\infty }\overbrace {V\otimes _{K}V\otimes _{K}\cdots \otimes _{K}V} ^{n}}
를 정의할 수 있다. 이 위에는 겹선형 이항 연산
⊗
:
T
m
(
V
)
⊗
K
T
n
(
V
)
→
T
m
+
n
(
V
)
{\displaystyle \otimes \colon T^{m}(V)\otimes _{K}T^{n}(V)\to T^{m+n}(V)}
(
u
1
⊗
u
2
⊗
⋯
u
m
)
⊗
(
v
1
⊗
v
2
⊗
⋯
v
n
)
=
u
1
⊗
u
2
⊗
⋯
u
m
⊗
v
1
⊗
v
2
⊗
⋯
v
n
)
{\displaystyle (u_{1}\otimes u_{2}\otimes \cdots u_{m})\otimes (v_{1}\otimes v_{2}\otimes \cdots v_{n})=u_{1}\otimes u_{2}\otimes \cdots u_{m}\otimes v_{1}\otimes v_{2}\otimes \cdots v_{n})}
이 정의되어 있으며, 이에 따라
T
(
V
)
{\displaystyle T(V)}
K
{\displaystyle K}
자연수 등급을 갖는 등급 단위 결합 대수 를 이룬다.
T
(
V
)
{\displaystyle T(V)}
아이디얼 을 생각하자.
I
=
(
{
v
⊗
v
:
v
∈
V
}
)
=
Span
{
v
1
⊗
v
2
⊗
⋯
v
n
:
∃
i
,
j
:
v
i
=
v
j
}
{\displaystyle I=(\{v\otimes v\colon v\in V\})=\operatorname {Span} \{v_{1}\otimes v_{2}\otimes \cdots v_{n}\colon \exists i,j\colon v_{i}=v_{j}\}}
그렇다면, 이 아이디얼에 대하여 몫대수를 취할 수 있으며, 이를 외대수
⋀
(
V
)
=
T
(
V
)
/
I
{\displaystyle \bigwedge (V)=T(V)/I}
⋀
(
V
)
=
⨁
n
=
0
∞
⋀
n
(
V
)
{\displaystyle \bigwedge (V)=\bigoplus _{n=0}^{\infty }\bigwedge ^{n}(V)}
라고 한다. 아이디얼에 대하여 몫을 취했으므로, 이 역시
K
{\displaystyle K}
단위 결합 대수 이다. 외대수에서의 이항 연산은 통상적으로
∧
:
⋀
m
V
⊗
⋀
n
V
→
⋀
m
+
n
V
{\displaystyle \wedge \colon \bigwedge ^{m}V\otimes \bigwedge ^{n}V\to \bigwedge ^{m+n}V}
α
∧
β
=
α
⊗
β
(
mod
I
)
{\displaystyle \alpha \wedge \beta =\alpha \otimes \beta {\pmod {I}}}
로 쓰며, 쐐기곱 (영어 : wedge product ) 또는 외적 (外積, 영어 : exterior product )이라고 한다.
외대수의
n
{\displaystyle n}
a
∈
⋀
n
V
{\displaystyle a\in \bigwedge ^{n}V}
n
{\displaystyle n}
영어 :
n
{\displaystyle n}
n
{\displaystyle n}
영어 :
n
{\displaystyle n}
n
{\displaystyle n}
영어 :
n
{\displaystyle n}
체
K
{\displaystyle K}
V
{\displaystyle V}
⋀
(
V
)
{\displaystyle \bigwedge (V)}
K
{\displaystyle K}
단위 결합 대수 이며, 자연수 등급을 갖는 등급 대수 이다. 또한, 이항 연산은 등급 가환 법칙을 따른다. 즉, 임의의
a
∈
⋀
m
V
{\displaystyle a\in \bigwedge ^{m}V}
b
∈
⋀
n
V
{\displaystyle b\in \bigwedge ^{n}V}
에 대하여,
a
∧
b
=
(
−
1
)
m
n
b
∧
a
{\displaystyle a\wedge b=(-1)^{mn}b\wedge a}
deg
(
a
∧
b
)
=
m
+
n
{\displaystyle \deg(a\wedge b)=m+n}
이다. 보다 일반적으로, 임의의
a
i
∈
⋀
n
i
V
(
i
=
1
,
2
,
…
,
k
)
{\displaystyle a_{i}\in \bigwedge ^{n_{i}}V\qquad (i=1,2,\dots ,k)}
및 순열
σ
∈
Sym
(
k
)
{\displaystyle \sigma \in \operatorname {Sym} (k)}
에 대하여,
a
σ
(
1
)
∧
a
σ
(
2
)
∧
⋯
∧
a
σ
(
k
)
=
(
−
1
)
σ
a
1
∧
a
2
∧
⋯
a
k
{\displaystyle a_{\sigma (1)}\wedge a_{\sigma (2)}\wedge \cdots \wedge a_{\sigma (k)}=(-1)^{\sigma }a_{1}\wedge a_{2}\wedge \cdots a_{k}}
이다. (이는
K
{\displaystyle K}
표수 가 2가 아니라면 쐐기곱의 등급 가환성과 동치이지만, 표수가 2일 경우에는 자명하지 않다.)
만약
V
{\displaystyle V}
dim
K
V
=
d
{\displaystyle \dim _{K}V=d}
dim
K
⋀
n
(
V
)
=
(
d
n
)
{\displaystyle \dim _{K}\bigwedge ^{n}(V)={\binom {d}{n}}}
dim
K
⋀
(
V
)
=
∑
n
=
0
d
(
d
n
)
=
2
d
{\displaystyle \dim _{K}\bigwedge (V)=\sum _{n=0}^{d}{\binom {d}{n}}=2^{d}}
이다. 즉,
⋀
(
V
)
{\displaystyle \bigwedge (V)}
0
,
1
,
…
,
d
{\displaystyle 0,1,\dots ,d}
같은 체 위의 임의의 두 벡터 공간
V
{\displaystyle V}
W
{\displaystyle W}
⋀
(
V
⊕
W
)
≅
⋀
V
⊗
⋀
W
{\displaystyle \bigwedge (V\oplus W)\cong \bigwedge V\otimes \bigwedge W}
⋀
n
(
V
⊕
W
)
≅
∑
p
+
q
=
n
⋀
p
V
⊗
⋀
q
W
{\displaystyle \bigwedge ^{n}(V\oplus W)\cong \sum _{p+q=n}\bigwedge ^{p}V\otimes \bigwedge ^{q}W}
함자성 [ 편집 ] 외대수는 벡터 공간의 범주
K
-Vect
{\displaystyle K{\text{-Vect}}}
K
{\displaystyle K}
단위 결합 대수 의 범주
K
-uAssoc
{\displaystyle K{\text{-uAssoc}}}
함자 를 정의한다. 구체적으로, 선형 변환
T
:
V
→
W
{\displaystyle T\colon V\to W}
에 대응하는 외대수 준동형 은 다음과 같다.
⋀
T
:
⋀
V
→
⋀
W
{\displaystyle \bigwedge T\colon \bigwedge V\to \bigwedge W}
⋀
T
:
v
1
∧
⋯
∧
v
n
↦
T
(
v
1
)
∧
⋯
∧
T
(
v
n
)
{\displaystyle \bigwedge T\colon v_{1}\wedge \cdots \wedge v_{n}\mapsto T(v_{1})\wedge \cdots \wedge T(v_{n})}
또한, 외대수 함자는 왼쪽 완전 함자 이다. 즉, 벡터 공간의 아벨 범주 에서의 짧은 완전열
0
→
U
→
V
→
W
→
0
{\displaystyle 0\to U\to V\to W\to 0}
이 주어졌을 때,
0
→
⋀
U
→
⋀
V
{\displaystyle 0\to \bigwedge U\to \bigwedge V}
는 완전열 이다. 또한,
0
→
⋀
1
U
∧
⋀
V
→
⋀
V
→
⋀
W
→
0
{\displaystyle 0\to \bigwedge ^{1}U\wedge \bigwedge V\to \bigwedge V\to \bigwedge W\to 0}
역시 완전열 이다.
호프 대수 구조 [ 편집 ] 외대수는 단위 결합 대수 의 구조뿐만 아니라, 호프 대수 의 구조를 갖는다. 이 경우, 쌍대곱(영어 : coproduct )은 다음과 같다.
Δ
:
⋀
n
V
→
⋀
n
V
⊗
⋀
n
V
{\displaystyle \Delta \colon \bigwedge ^{n}V\to \bigwedge ^{n}V\otimes \bigwedge ^{n}V}
Δ
(
v
1
∧
⋯
∧
v
n
)
=
∑
p
=
0
n
∑
σ
∈
Sh
(
p
,
n
−
p
)
(
−
1
)
σ
(
v
σ
(
1
)
∧
⋯
∧
v
σ
(
p
)
)
⊗
(
v
σ
(
p
+
1
)
∧
⋯
∧
v
σ
(
k
)
)
{\displaystyle \Delta (v_{1}\wedge \dots \wedge v_{n})=\sum _{p=0}^{n}\sum _{\sigma \in \operatorname {Sh} (p,n-p)}(-1)^{\sigma }(v_{\sigma (1)}\wedge \dots \wedge v_{\sigma (p)})\otimes (v_{\sigma (p+1)}\wedge \dots \wedge v_{\sigma (k)})}
여기서
Sh
(
p
,
k
−
p
)
⊂
Sym
(
n
)
{\displaystyle \operatorname {Sh} (p,k-p)\subset \operatorname {Sym} (n)}
(
p
,
n
−
p
)
{\displaystyle (p,n-p)}
셔플 순열 의 집합이다.
쌍대단위원(영어 : counit )은
ϵ
:
⋀
n
V
→
K
{\displaystyle \epsilon \colon \bigwedge ^{n}V\to K}
ϵ
:
v
↦
{
0
v
∈
⋀
n
V
,
n
>
0
v
v
∈
⋀
0
V
≅
K
{\displaystyle \epsilon \colon v\mapsto {\begin{cases}0&v\in \bigwedge ^{n}V,\qquad n>0\\v&v\in \bigwedge ^{0}V\cong K\end{cases}}}
이다. 앤티포드(영어 : antipode )는
S
:
⋀
n
V
→
⋀
n
V
{\displaystyle S\colon \bigwedge ^{n}V\to \bigwedge ^{n}V}
S
:
v
↦
(
−
)
deg
v
v
{\displaystyle S\colon v\mapsto (-)^{\deg v}v}
이다. (모든 연산들은 혼합 등급을 갖는 원소에 대하여 선형으로 정의된다.)
내적과 호지 쌍대 [ 편집 ]
V
{\displaystyle V}
실수체 위의 유한 차원 내적 공간 이라고 하자. 그렇다면
⋀
V
{\displaystyle \bigwedge V}
a
=
u
1
∧
u
2
∧
⋯
∧
u
m
∈
⋀
m
V
{\displaystyle a=u_{1}\wedge u_{2}\wedge \cdots \wedge u_{m}\in \bigwedge ^{m}V}
b
=
v
1
∧
v
2
∧
⋯
∧
v
n
∈
⋀
n
V
{\displaystyle b=v_{1}\wedge v_{2}\wedge \cdots \wedge v_{n}\in \bigwedge ^{n}V}
에 대하여,
⟨
a
,
b
⟩
=
{
det
(
⟨
a
i
,
b
j
⟩
)
i
j
m
=
n
0
m
≠
n
{\displaystyle \langle a,b\rangle ={\begin{cases}\det(\langle a_{i},b_{j}\rangle )_{ij}&m=n\\0&m\neq n\end{cases}}}
이다.
V
{\displaystyle V}
방향 이 주어졌다고 하자. 즉, 정규 직교 기저 의 순서
(
e
1
,
…
,
e
d
)
{\displaystyle (\mathbf {e} _{1},\dots ,\mathbf {e} _{d})}
⋀
V
{\displaystyle \bigwedge V}
호지 쌍대
∗
:
⋀
m
V
→
⋀
d
−
m
V
{\displaystyle *\colon \bigwedge ^{m}V\to \bigwedge ^{d-m}V}
∗
:
e
1
∧
⋯
∧
e
m
↦
e
m
+
1
∧
⋯
∧
e
d
{\displaystyle *\colon \mathbf {e} _{1}\wedge \cdots \wedge \mathbf {e} _{m}\mapsto \mathbf {e} _{m+1}\wedge \cdots \wedge \mathbf {e} _{d}}
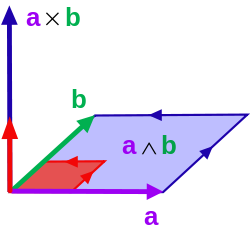
기하학적 해석 [ 편집 ] 두 변의 좌표로 만든 행렬의 행렬식의 관점에서 평행사변형의 넓이
V
{\displaystyle V}
⋀
n
V
{\displaystyle \bigwedge ^{n}V}
n
{\displaystyle n}
일차 독립 벡터들의 열
v
1
,
v
2
,
…
,
v
n
∈
V
{\displaystyle v_{1},v_{2},\dots ,v_{n}\in V}
이 주어졌을 때
v
1
∧
v
2
∧
⋯
∧
v
n
∈
⋀
n
V
{\displaystyle v_{1}\wedge v_{2}\wedge \cdots \wedge v_{n}\in \bigwedge ^{n}V}
는
{
v
i
}
i
=
1
,
…
,
n
{\displaystyle \{v_{i}\}_{i=1,\dots ,n}}
평행체 (영어 : parallelepiped )를 나타낸다.
V
{\displaystyle V}
노름
‖
v
1
∧
v
2
∧
⋯
∧
v
n
∈
⋀
n
V
‖
{\displaystyle \|v_{1}\wedge v_{2}\wedge \cdots \wedge v_{n}\in \bigwedge ^{n}V\|}
은 이 평행체의 초부피와 같다.
예를 들어,
n
=
1
{\displaystyle n=1}
⋀
1
V
≅
V
{\displaystyle \bigwedge ^{1}V\cong V}
V
{\displaystyle V}
n
=
2
{\displaystyle n=2}
u
∧
v
{\displaystyle u\wedge v}
u
{\displaystyle u}
v
{\displaystyle v}
평행사변형 을 나타내며, 노름을 취하면 평행사변형의 넓이를 얻는다.
3차원 벡터와의 관계 [ 편집 ] 쐐기곱 (연보라색 파란색 빨간색 연한 빨간색 3차원 유클리드 공간
R
3
{\displaystyle \mathbb {R} ^{3}}
⋀
0
R
3
≅
R
{\displaystyle \bigwedge ^{0}\mathbb {R} ^{3}\cong \mathbb {R} }
⋀
1
R
3
≅
R
3
{\displaystyle \bigwedge ^{1}\mathbb {R} ^{3}\cong \mathbb {R} ^{3}}
⋀
2
R
3
≅
R
3
{\displaystyle \bigwedge ^{2}\mathbb {R} ^{3}\cong \mathbb {R} ^{3}}
⋀
3
R
3
≅
R
{\displaystyle \bigwedge ^{3}\mathbb {R} ^{3}\cong \mathbb {R} }
이므로, 호지 쌍대 에 따라 외대수의 1차 및 2차 원소를 둘 다 3차원 벡터로 여길 수 있다.
이 경우, 외대수의 쐐기곱을 벡터의 벡터곱 으로 다음과 같이 나타낼 수 있다.
u
×
v
=
∗
(
u
∧
v
)
(
u
,
v
∈
R
3
)
{\displaystyle \mathbf {u} \times \mathbf {v} =*(\mathbf {u} \wedge \mathbf {v} )\qquad (u,v\in \mathbb {R} ^{3})}
즉, 3차원 벡터의 벡터곱 은 쐐기곱의 특수한 경우이다. 그러나 3차원이 아닌 다른 차원에서는
dim
⋀
1
V
≠
dim
⋀
2
V
{\displaystyle \dim \bigwedge ^{1}V\neq \dim \bigwedge ^{2}V}
마찬가지로, 3차원 벡터의 삼중곱 은 다음과 같이 쐐기곱으로 나타낼 수 있다.
u
⋅
v
×
w
=
∗
(
u
∧
v
∧
w
)
{\displaystyle \mathbf {u} \cdot \mathbf {v} \times \mathbf {w} =*(\mathbf {u} \wedge \mathbf {v} \wedge \mathbf {w} )}
헤르만 그라스만 이 1844년에 《선형 확장 이론: 수학의 새 분야》(독일어 : Die Lineale Ausdehnungslehre, ein neuer Zweig der Mathematik )[1] 독일어 : Ausdehnungslehre )이라고 불렀다. 이후 그라스만의 이론은 오랫동안 잊혀져 있다가, 1888년에 주세페 페아노 가 그의 이론을 재발견하였고 재조명하였다. 이후, 앙리 푸앵카레 · 엘리 카르탕 · 가스통 다르부 등에 의해, 미분 형식 의 형태로 현대 미분기하학 의 핵심적인 위치를 차지하게 되었다.
미분기하학 에서는 접다발 의 각 올인 접공간 에 각각 외대수를 취하여 얻는 벡터 다발 의 단면을 미분 형식
물리학 에서, 외대수는 페르미온 값을 갖는 장들을 나타내기 위하여 쓰인다. 이들은 반가환수 의 값을 갖는데, 반가환수는 외대수의 원소로 정의할 수 있다. 또한, 초대칭 이론의 경우 초장 들은 초다양체 위에 정의되는데, 이는 국소적으로 외대수를 갖춘 유클리드 공간 매끄러운 함수 환과 동형인 층 을 갖춘 위상 공간 이다.
참고 문헌 [ 편집 ] 외부 링크 [ 편집 ] 같이 보기 [ 편집 ]