중간값 정리 해석학 에서 중간값 정리 [1] 영어 : intermediate value theorem ) 또는 사잇값 정리 [2] :78 구간 에 정의된 실숫값 연속 함수 가 임의의 두 함숫값 사이의 모든 수를 함숫값으로 포함한다는 정리이다. 이에 따라, 실숫값 연속 함수에 대한 구간의 상 은 구간이다.
연속 함수
f
:
[
a
,
b
]
→
R
{\displaystyle f\colon [a,b]\to \mathbb {R} }
중간값 정리 에 따르면, 다음이 성립한다.
f
(
[
a
,
b
]
)
⊇
[
f
(
a
)
,
f
(
b
)
]
∪
[
f
(
b
)
,
f
(
a
)
]
{\displaystyle f([a,b])\supseteq [f(a),f(b)]\cup [f(b),f(a)]}
즉, 임의의
u
∈
(
f
(
a
)
,
f
(
b
)
)
∪
(
f
(
b
)
,
f
(
a
)
)
{\displaystyle u\in (f(a),f(b))\cup (f(b),f(a))}
c
∈
(
a
,
b
)
{\displaystyle c\in (a,b)}
[3]
f
(
c
)
=
u
{\displaystyle f(c)=u}
편의상
f
(
a
)
<
f
(
b
)
{\displaystyle f(a)<f(b)}
f
(
a
)
<
u
<
f
(
b
)
{\displaystyle f(a)<u<f(b)}
E
=
{
x
∈
[
a
,
b
]
:
f
(
x
)
<
u
}
{\displaystyle E=\{x\in [a,b]\colon f(x)<u\}}
그렇다면,
a
∈
E
{\displaystyle a\in E}
b
{\displaystyle b}
E
{\displaystyle E}
E
{\displaystyle E}
c
=
sup
E
∈
R
{\displaystyle c=\sup E\in \mathbb {R} }
를 갖는다.
f
{\displaystyle f}
δ
>
0
{\displaystyle \delta >0}
f
(
x
)
<
u
∀
a
≤
x
<
a
+
δ
{\displaystyle f(x)<u\qquad \forall a\leq x<a+\delta }
f
(
x
)
>
u
∀
b
−
δ
<
x
≤
b
{\displaystyle f(x)>u\qquad \forall b-\delta <x\leq b}
따라서
a
<
c
<
b
{\displaystyle a<c<b}
귀류법 을 사용하여
f
(
c
)
=
u
{\displaystyle f(c)=u}
f
(
c
)
>
u
{\displaystyle f(c)>u}
f
{\displaystyle f}
η
>
0
{\displaystyle \eta >0}
f
(
x
)
>
u
∀
c
−
η
<
x
<
c
+
η
{\displaystyle f(x)>u\qquad \forall c-\eta <x<c+\eta }
즉,
c
−
η
{\displaystyle c-\eta }
E
{\displaystyle E}
c
−
η
<
c
{\displaystyle c-\eta <c}
f
(
c
)
<
u
{\displaystyle f(c)<u}
f
{\displaystyle f}
η
>
0
{\displaystyle \eta >0}
f
(
x
)
<
u
∀
c
−
η
<
x
<
c
+
η
{\displaystyle f(x)<u\qquad \forall c-\eta <x<c+\eta }
즉,
c
+
η
/
2
∈
E
{\displaystyle c+\eta /2\in E}
c
=
sup
E
{\displaystyle c=\sup E}
f
(
c
)
=
u
{\displaystyle f(c)=u}
따름정리 [ 편집 ] 볼차노 정리 [ 편집 ] 연속 함수
f
:
[
a
,
b
]
→
R
{\displaystyle f\colon [a,b]\to \mathbb {R} }
f
(
a
)
f
(
b
)
<
0
{\displaystyle f(a)f(b)<0}
볼차노 정리 (영어 : Bolzano's theorem )에 따르면,
f
{\displaystyle f}
(
a
,
b
)
{\displaystyle (a,b)}
영점 을 갖는다. 즉, 다음을 만족시키는
c
∈
(
a
,
b
)
{\displaystyle c\in (a,b)}
f
(
c
)
=
0
{\displaystyle f(c)=0}
볼차노 정리는 중간값 정리에서
u
=
0
{\displaystyle u=0}
구간의 보존 [ 편집 ] 구간
I
⊆
R
{\displaystyle I\subseteq \mathbb {R} }
f
:
I
→
R
{\displaystyle f\colon I\to \mathbb {R} }
I
{\displaystyle I}
f
(
I
)
{\displaystyle f(I)}
연결 공간 의 개념을 사용하지 않고 증명하려면,
I
⊆
R
{\displaystyle I\subseteq \mathbb {R} }
a
,
b
∈
I
{\displaystyle a,b\in I}
(
a
,
b
)
⊆
I
{\displaystyle (a,b)\subseteq I}
특히, 만약
I
=
[
a
,
b
]
{\displaystyle I=[a,b]}
f
(
I
)
{\displaystyle f(I)}
f
{\displaystyle f}
최댓값 과 최솟값 이다. 즉, 다음이 성립한다.
f
(
[
a
,
b
]
)
=
[
min
x
∈
[
a
,
b
]
f
(
x
)
,
max
x
∈
[
a
,
b
]
f
(
x
)
]
{\displaystyle f([a,b])=\left[\min _{x\in [a,b]}f(x),\max _{x\in [a,b]}f(x)\right]}
이 정리는 중간값 정리와 최대 최소 정리 를 사용하여 증명할 수 있다.
홀수차 실수 다항식의 근의 존재 [ 편집 ] 임의의 실수 홀수 차 다항식 은 적어도 하나의 실수 영점을 갖는다. 이는 대수학의 기본 정리 의 자명한 경우이며, 중간값 정리를 사용하여 다음과 같이 증명할 수 있다.
홀수차 실수 다항식
p
(
x
)
=
a
2
n
+
1
x
2
n
+
1
+
a
2
n
x
2
n
+
⋯
+
a
1
x
+
a
0
∈
R
[
x
]
(
a
0
,
…
,
a
2
n
+
1
∈
R
,
a
2
n
+
1
≠
0
)
{\displaystyle p(x)=a_{2n+1}x^{2n+1}+a_{2n}x^{2n}+\cdots +a_{1}x+a_{0}\in \mathbb {R} [x]\qquad (a_{0},\dots ,a_{2n+1}\in \mathbb {R} ,\;a_{2n+1}\neq 0)}
이 주어졌다고 하자. 편의상
a
2
n
+
1
>
0
{\displaystyle a_{2n+1}>0}
lim
x
→
−
∞
p
(
x
)
=
−
∞
,
lim
x
→
∞
p
(
x
)
=
∞
{\displaystyle \lim _{x\to -\infty }p(x)=-\infty ,\;\lim _{x\to \infty }p(x)=\infty }
예를 들어, 전자의 경우 다음과 같이 보일 수 있다.
lim
x
→
−
∞
p
(
x
)
=
lim
x
→
−
∞
a
2
n
+
1
x
2
n
+
1
(
1
+
a
2
n
a
2
n
+
1
x
−
1
+
⋯
+
a
0
a
2
n
+
1
x
−
(
2
n
+
1
)
)
=
−
∞
{\displaystyle {\begin{aligned}\lim _{x\to -\infty }p(x)&=\lim _{x\to -\infty }a_{2n+1}x^{2n+1}\left(1+{\frac {a_{2n}}{a_{2n+1}}}x^{-1}+\cdots +{\frac {a_{0}}{a_{2n+1}}}x^{-(2n+1)}\right)\\&=-\infty \end{aligned}}}
이에 따라, 다음을 만족시키는
c
<
0
<
d
{\displaystyle c<0<d}
p
(
c
)
<
0
<
p
(
d
)
{\displaystyle p(c)<0<p(d)}
중간값 정리를
p
|
[
c
,
d
]
{\displaystyle p|_{[c,d]}}
p
{\displaystyle p}
e
∈
(
c
,
d
)
{\displaystyle e\in (c,d)}
닫힌구간 위의 브라우어르 고정점 정리 [ 편집 ] 연속 함수
f
:
[
a
,
b
]
→
[
a
,
b
]
{\displaystyle f\colon [a,b]\to [a,b]}
고정점 을 갖는다. 즉, 다음을 만족시키는
c
∈
[
a
,
b
]
{\displaystyle c\in [a,b]}
f
(
c
)
=
c
{\displaystyle f(c)=c}
이는 브라우어르 고정점 정리 의 자명한 경우이며, 중간값 정리를 사용하여 다음과 같이 증명할 수 있다.
다음과 같은 함수
g
:
[
a
,
b
]
→
R
{\displaystyle g\colon [a,b]\to \mathbb {R} }
g
(
x
)
=
f
(
x
)
−
x
∀
x
∈
[
a
,
b
]
{\displaystyle g(x)=f(x)-x\qquad \forall x\in [a,b]}
그렇다면,
g
{\displaystyle g}
g
(
b
)
≤
0
≤
g
(
a
)
{\displaystyle g(b)\leq 0\leq g(a)}
c
∈
[
a
,
b
]
{\displaystyle c\in [a,b]}
g
(
c
)
=
0
{\displaystyle g(c)=0}
즉,
f
(
c
)
=
c
{\displaystyle f(c)=c}
가역 연속 함수의 단조성 [ 편집 ] 구간
I
⊆
R
{\displaystyle I\subseteq \mathbb {R} }
단사 연속 함수
f
:
I
→
R
{\displaystyle f\colon I\to \mathbb {R} }
f
{\displaystyle f}
순단조 함수 이다. 이는 중간값 정리를 통해 다음과 같이 증명할 수 있다.
귀류법 을 사용하여,
f
{\displaystyle f}
a
,
b
,
c
∈
I
{\displaystyle a,b,c\in I}
a
<
b
<
c
{\displaystyle a<b<c}
f
(
a
)
<
f
(
b
)
>
f
(
c
)
{\displaystyle f(a)<f(b)>f(c)}
f
(
a
)
>
f
(
b
)
<
f
(
c
)
{\displaystyle f(a)>f(b)<f(c)}
편의상 전자가 성립한다고 가정하자. 그렇다면,
max
{
f
(
a
)
,
f
(
c
)
}
<
u
<
f
(
b
)
{\displaystyle \max\{f(a),f(c)\}<u<f(b)}
f
|
[
a
,
b
]
{\displaystyle f|_{[a,b]}}
f
|
[
b
,
c
]
{\displaystyle f|_{[b,c]}}
d
∈
(
a
,
b
)
{\displaystyle d\in (a,b)}
e
∈
(
b
,
c
)
{\displaystyle e\in (b,c)}
f
(
d
)
=
f
(
e
)
=
u
{\displaystyle f(d)=f(e)=u}
이는
f
{\displaystyle f}
일반화 [ 편집 ] 위상수학과 해석학의 몇몇 정리들은 중간값 정리를 특수한 경우로 포함한다.
연결 공간의 보존 [ 편집 ] 두 위상 공간
X
,
Y
{\displaystyle X,Y}
f
:
X
→
Y
{\displaystyle f\colon X\to Y}
X
{\displaystyle X}
연결 공간 이라면,
f
(
X
)
{\displaystyle f(X)}
R
{\displaystyle \mathbb {R} }
위상 공간
X
{\displaystyle X}
순서 위상 을 부여한) 전순서 집합
(
Y
,
≤
)
{\displaystyle (Y,\leq )}
f
:
X
→
Y
{\displaystyle f\colon X\to Y}
X
{\displaystyle X}
a
,
b
∈
X
{\displaystyle a,b\in X}
f
(
X
)
⊇
[
f
(
a
)
,
f
(
b
)
]
∪
[
f
(
b
)
,
f
(
a
)
]
{\displaystyle f(X)\supseteq [f(a),f(b)]\cup [f(b),f(a)]}
실수 집합
R
{\displaystyle \mathbb {R} }
다르부 정리 [ 편집 ] 미분 가능 함수
f
:
[
a
,
b
]
→
R
{\displaystyle f\colon [a,b]\to \mathbb {R} }
f
′
(
[
a
,
b
]
)
⊇
[
f
′
(
a
)
,
f
′
(
b
)
]
∪
[
f
′
(
b
)
,
f
′
(
a
)
]
{\displaystyle f'([a,b])\supseteq [f'(a),f'(b)]\cup [f'(b),f'(a)]}
이를 다르부 정리 라고 한다. 실수 연속 함수는 항상 어떤 함수의 도함수 이므로, 다르부 정리는 중간값 정리의 일반화이다.
외부 링크 [ 편집 ] 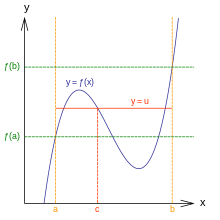

![{\displaystyle f\colon [a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5ab61178bf5349838758ffe3d96135406ed0245)
![{\displaystyle f([a,b])\supseteq [f(a),f(b)]\cup [f(b),f(a)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78b17c51cb2b100edbfab838d8c618fc9729984f)





![{\displaystyle E=\{x\in [a,b]\colon f(x)<u\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ceef632ea5610f6ce3e4983bb671b9eae3e7d1a)




























![{\displaystyle I=[a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d6214bb3ce7f00e496c0706edd1464ac60b73b5)
![{\displaystyle f([a,b])=\left[\min _{x\in [a,b]}f(x),\max _{x\in [a,b]}f(x)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5fd1828d89b6431af75d5d999edc674794f8b620)
![{\displaystyle p(x)=a_{2n+1}x^{2n+1}+a_{2n}x^{2n}+\cdots +a_{1}x+a_{0}\in \mathbb {R} [x]\qquad (a_{0},\dots ,a_{2n+1}\in \mathbb {R} ,\;a_{2n+1}\neq 0)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4144f55e03cdea1196444d735e76a1c9ba09a2f3)





![{\displaystyle p|_{[c,d]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/221fc99f03b4804d7953524191b166d44cd0a6e1)


![{\displaystyle f\colon [a,b]\to [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46068842a3caaf3620f67ee4bfc9c15cd6e1ed50)
![{\displaystyle c\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/997256364b06acf0710e5d24da39e8c42991a249)

![{\displaystyle g\colon [a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/38132af5ea7cd916293fe93f29187bd461a5e270)
![{\displaystyle g(x)=f(x)-x\qquad \forall x\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f53fd9a10b32601bfb7daefb3480a83c76edaf4a)








![{\displaystyle f|_{[a,b]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/130a868ae110727636a44bb6418af4d312c13835)
![{\displaystyle f|_{[b,c]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/360d4260c2096764237cba6488af6df08d1b2b7b)










![{\displaystyle f(X)\supseteq [f(a),f(b)]\cup [f(b),f(a)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d892da298236192b459392134c85c49e2ebbac30)
![{\displaystyle f'([a,b])\supseteq [f'(a),f'(b)]\cup [f'(b),f'(a)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6772c2b5a491a0376a00b1856a4d27295a4e23f6)