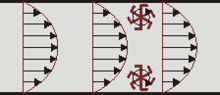
수학 에서 회전 (回轉, 영어 : curl 컬[* ] )은 3차원 벡터장을 다른 3차원 벡터장으로 대응시키는 1차 미분 연산자의 하나이다. 수식에서 기호는 "
∇
×
{\displaystyle \nabla \times }
curl
(
)
{\displaystyle \operatorname {curl} ()}
직교 좌표계에서의 정의 [ 편집 ] 어떤 벡터장 F =F1 i +F2 j +F3 k 의 회전 은
다음과 같이 표현되는 기호 행렬식 이다.
∇
×
F
=
det
(
i
j
k
∂
/
∂
x
∂
/
∂
y
∂
/
∂
z
F
1
F
2
F
3
)
=
(
∂
F
3
∂
y
−
∂
F
2
∂
z
)
i
+
(
∂
F
1
∂
z
−
∂
F
3
∂
x
)
j
+
(
∂
F
2
∂
x
−
∂
F
1
∂
y
)
k
{\displaystyle \nabla \times \mathbf {F} =\det {\begin{pmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\\partial /\partial x&\partial /\partial y&\partial /\partial z\\F_{1}&F_{2}&F_{3}\\\end{pmatrix}}=\left({\frac {\partial F_{3}}{\partial y}}-{\frac {\partial F_{2}}{\partial z}}\right)\mathbf {i} +\left({\frac {\partial F_{1}}{\partial z}}-{\frac {\partial F_{3}}{\partial x}}\right)\mathbf {j} +\left({\frac {\partial F_{2}}{\partial x}}-{\frac {\partial F_{1}}{\partial y}}\right)\mathbf {k} }
만일 왼손좌표계의 경우에는 위의 행렬식에 음의 부호를 취한다.
좌표계 독립적인 정의 [ 편집 ] 위의 정의는 직교 좌표계 를 사용하여 정의를 하였다. 그러나 어떠한 좌표계 에서든지 성립하는 회전의 정의도 존재하며 많은 물리책들은 위의 정의 대신 다음 정의를 사용한다. 그 정의는 다음과 같다.
어떤 점에서의 벡터장 의 회전은 그 점을 포함하는 임의의 닫힌 곡면 S에서 바깥방향 법선벡터 와 그 벡터장 의 벡터곱 의 면적분 과 그 곡면으로 둘러싸인 부피(V)의 비를 부피를 0으로 보낼 때의 극한이다. 수식으로 표현하면 다음과 같다.
∇
×
F
=
lim
V
→
0
1
V
∮
S
n
×
F
d
a
{\displaystyle \nabla \times \mathbf {F} =\lim _{V\to 0}{\frac {1}{V}}\oint _{S}\mathbf {n} \times \mathbf {F} \,da}
계산의 편리성과 물리적 의미의 이해를 돕기 위하여 여러 가지 연산을 통해 적분속에 있는 벡터곱 을 없애줄 수 있으며, 그 결과는 다음과 같다.
어떤 점에서
∇
×
F
{\displaystyle \nabla \times \mathbf {F} }
단위벡터 a 방향 성분은 그 점을 포함하는 a 에 수직한 평면 S'에서 그 둘레 C를 따라 F 를 선적분 한 값과 S'의 넓이의 비를 넓이를 0으로 보낼 때의 극한이다. 수식으로 표현하면 다음과 같다.
a
^
⋅
∇
×
F
=
lim
S
′
→
0
1
S
′
∮
C
F
⋅
d
l
{\displaystyle {\hat {\mathbf {a} }}\cdot \nabla \times \mathbf {F} =\lim _{S'\to 0}{\frac {1}{S'}}\oint _{C}\mathbf {F} \cdot d\mathbf {l} }
회전 성분에 관한 정리의 증명 [ 편집 ] 벡터곱 을 이용한 정의로부터 이 성질을 유도해보자. 일단 단위벡터 a 는 상수이므로,
a
^
⋅
∇
×
F
=
lim
V
→
0
1
V
a
^
⋅
∮
S
n
×
F
d
a
=
lim
V
→
0
1
V
∮
S
a
^
⋅
(
n
×
F
)
d
a
=
lim
V
→
0
1
V
∮
S
F
⋅
(
a
^
×
n
)
d
a
{\displaystyle {\hat {\mathbf {a} }}\cdot \nabla \times \mathbf {F} =\lim _{V\to 0}{\frac {1}{V}}{\hat {\mathbf {a} }}\cdot \oint _{S}\mathbf {n} \times \mathbf {F} \,da=\lim _{V\to 0}{\frac {1}{V}}\oint _{S}{\hat {\mathbf {a} }}\cdot \left(\mathbf {n} \times \mathbf {F} \right)da=\lim _{V\to 0}{\frac {1}{V}}\oint _{S}\mathbf {F} \cdot \left({\hat {\mathbf {a} }}\times \mathbf {n} \right)da}
(스칼라 삼중곱 의 성질에 의하여 순서를 바꾸어 줄 수 있다.)
여기서 적분할 부피를 잘 잡아주면 식을 간단히 정리할 수 있다. 아래 정의에서 적분에 사용한 평면 S'을 단위벡터 a 를 따라 ξ/2만큼, -a 를 따라 ξ/2만큼 평행이동할 때 면이 쓸고 지나가는 공간에 대하여 생각해보자. 이 공간은 부피가 S'ξ인 일종의 기둥이 된다. 기둥의 밑면 에서의 a ×n 은 n 과 a 가 평행하므로 0이된다. 즉, 기둥의 밑면 에 대한 면적분 은 0이되고, 옆면 Sside 에 대해서만 면적분 을 해주면 된다. 이 면적분 은 다르게 말하면 밑면에 평행하게 무한히 많은 층으로 잘라서(dh), 각 층에서 둘레를 따라(dl) 선적분 한것들의 총합이 될 것이다. 수식으로 나타내면 다음과 같다.
a
^
⋅
∇
×
F
=
lim
V
→
0
1
V
∬
S
s
i
d
e
F
⋅
(
a
^
×
n
)
d
a
=
lim
V
→
0
1
V
∮
C
∫
−
ξ
2
ξ
2
F
⋅
(
a
^
×
n
)
d
h
d
l
{\displaystyle {\hat {\mathbf {a} }}\cdot \nabla \times \mathbf {F} =\lim _{V\to 0}{\frac {1}{V}}\iint _{S_{side}}\mathbf {F} \cdot \left({\hat {\mathbf {a} }}\times \mathbf {n} \right)da=\lim _{V\to 0}{\frac {1}{V}}\oint _{C}\int _{-{\frac {\xi }{2}}}^{\xi \over 2}\mathbf {F} \cdot \left({\hat {\mathbf {a} }}\times \mathbf {n} \right)dhdl}
F 는 연속이므로[1] 평균값 정리 를 사용해준다면 특정한 F * 에 대하여 다음과 같이 나타낼 수 있다.
a
^
⋅
∇
×
F
=
lim
V
→
0
1
V
∮
C
ξ
F
∗
⋅
(
a
^
×
n
)
d
l
{\displaystyle {\hat {\mathbf {a} }}\cdot \nabla \times \mathbf {F} =\lim _{V\to 0}{\frac {1}{V}}\oint _{C}\xi \mathbf {F} ^{*}\cdot \left({\hat {\mathbf {a} }}\times \mathbf {n} \right)dl}
옆면에서 a ×n 을 생각해보면 둘레에 평행한 단위벡터 이다. 따라서 (a ×n )dl을 dl 로 바꾸어줄 수 있다. 부피 V는 기둥의 부피 공식에 의하여 밑면의 넓에 S'에 높이 ξ를 곱한 것이 되므로 적분 속에 있는 ξ와 약분이 된다. 또한 V가 0으로 가면 S'도 0으로 갈 것이고, ξ도 0으로 가므로, F * 도 F로 갈 것이다. 정리하면 다음과 같다.
a
^
⋅
∇
×
F
=
lim
V
→
0
ξ
S
′
ξ
∮
C
F
∗
⋅
d
l
=
lim
S
′
→
0
1
S
′
∮
C
F
⋅
d
l
{\displaystyle {\hat {\mathbf {a} }}\cdot \nabla \times \mathbf {F} =\lim _{V\to 0}{\frac {\xi }{S'\xi }}\oint _{C}\mathbf {F} ^{*}\cdot d\mathbf {l} =\lim _{S'\to 0}{\frac {1}{S'}}\oint _{C}\mathbf {F} \cdot d\mathbf {l} }
직교 좌표계 정의의 유도 [ 편집 ] 위의 정리를 사용하여 회전의 x방향 성분을 생각해보자. 미소 ε에 대하여 (x, y, z), (x, y+ε, z), (x, y+ε, z+ε), (x, y, z+ε)을 꼭짓점으로 갖는 정사각형을 생각해 보자. 그 정사각형에서 위의 정리를 사용하면 다음과 같다.
i
^
⋅
∇
×
F
=
lim
S
→
0
1
S
∮
C
F
⋅
d
l
=
lim
ϵ
→
0
1
ϵ
2
(
∫
y
y
+
ϵ
F
2
(
x
,
y
′
,
z
)
d
y
′
+
∫
z
z
+
ϵ
F
3
(
x
,
y
+
ϵ
,
z
′
)
d
z
′
+
∫
y
+
ϵ
y
F
2
(
x
,
y
′
,
z
+
ϵ
)
d
y
′
+
∫
z
+
ϵ
z
F
3
(
x
,
y
,
z
′
)
d
z
′
)
=
lim
ϵ
→
0
1
ϵ
2
(
∫
z
z
+
ϵ
F
3
(
x
,
y
+
ϵ
,
z
′
)
−
F
3
(
x
,
y
,
z
′
)
d
z
′
−
∫
y
y
+
ϵ
F
2
(
x
,
y
′
,
z
+
ϵ
)
−
F
2
(
x
,
y
′
,
z
)
d
y
′
)
{\displaystyle {\begin{aligned}{\hat {\mathbf {i} }}\cdot \nabla \times \mathbf {F} &=\lim _{S\to 0}{\frac {1}{S}}\oint _{C}\mathbf {F} \cdot d\mathbf {l} \\&=\lim _{\epsilon \to 0}{\frac {1}{\epsilon ^{2}}}\left(\int _{y}^{y+\epsilon }F_{2}\left(x,y',z\right)dy'+\int _{z}^{z+\epsilon }F_{3}\left(x,y+\epsilon ,z'\right)dz'+\int _{y+\epsilon }^{y}F_{2}\left(x,y',z+\epsilon \right)dy'+\int _{z+\epsilon }^{z}F_{3}\left(x,y,z'\right)dz'\right)\\&=\lim _{\epsilon \to 0}{\frac {1}{\epsilon ^{2}}}\left(\int _{z}^{z+\epsilon }F_{3}\left(x,y+\epsilon ,z'\right)-F_{3}\left(x,y,z'\right)dz'-\int _{y}^{y+\epsilon }F_{2}\left(x,y',z+\epsilon \right)-F_{2}\left(x,y',z\right)dy'\right)\end{aligned}}}
첫번째 적분과 두번째 적분에 평균값 정리 의 미분 형태를 사용해주면 다음과 같다.
i
^
⋅
∇
×
F
=
lim
ϵ
→
0
1
ϵ
2
(
∫
z
z
+
ϵ
ϵ
∂
F
3
∂
y
(
x
,
y
¯
,
z
′
)
d
z
′
−
∫
y
y
+
ϵ
ϵ
∂
F
2
∂
z
(
x
,
y
′
,
z
¯
)
d
y
′
)
,
y
¯
∈
(
y
,
y
+
ϵ
)
,
z
¯
∈
(
z
,
z
+
ϵ
)
=
lim
ϵ
→
0
1
ϵ
(
∫
z
z
+
ϵ
∂
F
3
∂
y
(
x
,
y
¯
,
z
′
)
d
z
′
−
∫
y
y
+
ϵ
∂
F
2
∂
z
(
x
,
y
′
,
z
¯
)
d
y
′
)
{\displaystyle {\begin{aligned}{\hat {\mathbf {i} }}\cdot \nabla \times \mathbf {F} &=\lim _{\epsilon \to 0}{\frac {1}{\epsilon ^{2}}}\left(\int _{z}^{z+\epsilon }\epsilon {\frac {\partial F_{3}}{\partial y}}\left(x,{\bar {y}},z'\right)dz'-\int _{y}^{y+\epsilon }\epsilon {\frac {\partial F_{2}}{\partial z}}\left(x,y',{\bar {z}}\right)dy'\right),{\bar {y}}\in \left(y,y+\epsilon \right),{\bar {z}}\in \left(z,z+\epsilon \right)\\&=\lim _{\epsilon \to 0}{\frac {1}{\epsilon }}\left(\int _{z}^{z+\epsilon }{\frac {\partial F_{3}}{\partial y}}\left(x,{\bar {y}},z'\right)dz'-\int _{y}^{y+\epsilon }{\partial F_{2} \over \partial z}\left(x,y',{\bar {z}}\right)dy'\right)\end{aligned}}}
이제 첫번째와 두번째 적분에 평균값 정리 의 적분 형태를 사용해주면 다음과 같다.
i
^
⋅
∇
×
F
=
lim
ϵ
→
0
1
ϵ
(
ϵ
∂
F
3
∂
y
(
x
,
y
¯
,
z
~
)
−
ϵ
∂
F
2
∂
z
(
x
,
y
~
,
z
¯
)
)
,
y
~
∈
(
y
,
y
+
ϵ
)
,
z
~
∈
(
z
,
z
+
ϵ
)
=
lim
ϵ
→
0
(
∂
F
3
∂
y
(
x
,
y
¯
,
z
~
)
−
∂
F
2
∂
z
(
x
,
y
~
,
z
¯
)
)
{\displaystyle {\begin{aligned}{\hat {\mathbf {i} }}\cdot \nabla \times \mathbf {F} &=\lim _{\epsilon \to 0}{\frac {1}{\epsilon }}\left(\epsilon {\partial F_{3} \over \partial y}\left(x,{\bar {y}},{\tilde {z}}\right)-\epsilon {\partial F_{2} \over \partial z}\left(x,{\tilde {y}},{\bar {z}}\right)\right),{\tilde {y}}\in \left(y,y+\epsilon \right),{\tilde {z}}\in \left(z,z+\epsilon \right)\\&=\lim _{\epsilon \to 0}\left({\partial F_{3} \over \partial y}\left(x,{\bar {y}},{\tilde {z}}\right)-{\partial F_{2} \over \partial z}\left(x,{\tilde {y}},{\bar {z}}\right)\right)\end{aligned}}}
ε이 0으로 가면, 샌드위치 정리 에 의하여
y
¯
→
y
,
z
¯
→
z
,
y
~
→
y
,
z
~
→
z
{\displaystyle {\bar {y}}\to y,{\bar {z}}\to z,{\tilde {y}}\to y,{\tilde {z}}\to z}
i
^
⋅
∇
×
F
=
∂
F
3
∂
y
−
∂
F
2
∂
z
{\displaystyle {\hat {\mathbf {i} }}\cdot \nabla \times \mathbf {F} ={\partial F_{3} \over \partial y}-{\partial F_{2} \over \partial z}}
y방향, z방향 성분들도 위와 같은 과정을 걸치면 다음을 얻을 수 있다.
j
^
⋅
∇
×
F
=
∂
F
1
∂
z
−
∂
F
3
∂
x
{\displaystyle {\hat {\mathbf {j} }}\cdot \nabla \times \mathbf {F} ={\partial F_{1} \over \partial z}-{\partial F_{3} \over \partial x}}
k
^
⋅
∇
×
F
=
∂
F
2
∂
x
−
∂
F
1
∂
y
{\displaystyle {\hat {\mathbf {k} }}\cdot \nabla \times \mathbf {F} ={\partial F_{2} \over \partial x}-{\partial F_{1} \over \partial y}}
이는 위에서 소개된 직교 좌표계 에서의 회전의 정의와 같다.
물리적 의미 [ 편집 ] 어떤 강체 가 축을 중심으로 각속도 ω 로 회전하고 있다. 그리고 이 강체 각 부분의 속도 의 벡터장 을 V 라고하자. z축을 축으로 잡는다면 각속도
ω
=
ω
k
{\displaystyle {\boldsymbol {\omega }}=\omega \mathbf {k} }
V
(
x
,
y
,
z
)
=
ω
×
r
=
ω
k
×
(
x
i
+
y
j
)
=
ω
x
j
−
ω
y
i
{\displaystyle \mathbf {V} \left(x,y,z\right)={\boldsymbol {\omega }}\times \mathbf {r} =\omega \mathbf {k} \times (x\mathbf {i} +y\mathbf {j} )=\omega x\mathbf {j} -\omega y\mathbf {i} }
이다. V 의 회전 을 계산해본다면
∇
×
V
=
det
(
i
j
k
∂
∂
x
∂
∂
y
∂
∂
z
−
ω
y
ω
x
0
)
=
2
ω
k
=
2
ω
{\displaystyle \nabla \times \mathbf {V} =\det {\begin{pmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\{\frac {\partial }{\partial x}}&{\frac {\partial }{\partial y}}&{\frac {\partial }{\partial z}}\\-\omega y&\omega x&0\end{pmatrix}}=2\omega \mathbf {k} =2{\boldsymbol {\omega }}}
즉 각속도 와 연관이 있다. 따라서
∇
×
V
=
0
{\displaystyle \nabla \times \mathbf {V} =\mathbf {0} }
강체 는 회전하고 있지 않다는 것을 의미한다.
그렇다면 이제 유체 를 생각해보자. 유체의 한 지점에서 회전은 그 지점에 놓인 강체 의 각속도 의 2배이다. 만약 그 지점의 회전이 0 0
↑ 회전도 일종의 미분연산이다. 만약 연속하지 않으면 극한은 발산하며 그 점에서 회전은 정의될 수 없다.
참고 문헌 [ 편집 ] Marsden, Jerrold E.; Anthony J. Tromba (2003). 《Vector Calculus》 5판. W. H. Freeman and Company. ISBN 0-7167-4992-0 Reitz, John R.; Frederick Milford, Robert W. Christy (2009). 《Foundations of Electromagnetic Theory》 4판. Pearson Education Korea. ISBN 89-450-0112-3