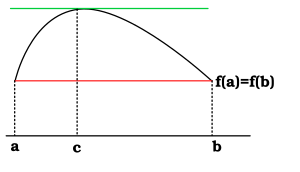
미적분학에서 롤의 정리(Rolle's theorem)란 미분 가능한 함수에 대한 본질적인 성질로서, 함수값이 같은 두 점이 존재할 경우, 함수의 그래프를 그리면 그 두 값 사이에 접선의 기울기가 0이 되는 점이 반드시 존재한다는 정리이다.
정리의 표준적 서술[편집]
실변수 함수  가 닫힌 구간 [a,b]에서 연속이고 열린 구간 (a,b)에서 미분 가능하며
가 닫힌 구간 [a,b]에서 연속이고 열린 구간 (a,b)에서 미분 가능하며  일 때,
일 때,  이 되는 구간 (a,b)사이의 c가 최소한 하나는 존재한다.
이 되는 구간 (a,b)사이의 c가 최소한 하나는 존재한다.
이것은 평균값 정리(mean value theorem)를 증명하는데 이용되며, 실질적으로 평균값 정리의 특별한 경우이다.
![{\displaystyle \left[a,b\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f30926fb280a9fdf66fd931e14d4363cb824feaa) 에서
에서  가 상수 함수인 경우
가 상수 함수인 경우
- 모든
 에 대해서
에 대해서  이다.
이다.
 인
인  가 존재할 경우
가 존재할 경우
- 최대 최소 정리에 의하여 함수
 는
는 ![{\displaystyle \left[a,b\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f30926fb280a9fdf66fd931e14d4363cb824feaa) 에서 최댓값을 갖는다.
에서 최댓값을 갖는다.  이며 가정에 의하여
이며 가정에 의하여  인
인  가 존재하므로 최댓값은
가 존재하므로 최댓값은  나
나  가 될 수 없다. 즉,
가 될 수 없다. 즉,  에서 최댓값을 가져야 한다.
에서 최댓값을 가져야 한다.  에서 최댓값을 가진다고 하면 일계도함수판정법에 의하여
에서 최댓값을 가진다고 하면 일계도함수판정법에 의하여  이다.
이다.
 인
인  가 존재할 경우
가 존재할 경우
- 최대 최소 정리에 의하여 함수
 는
는 ![{\displaystyle \left[a,b\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f30926fb280a9fdf66fd931e14d4363cb824feaa) 에서 최솟값을 갖는다.
에서 최솟값을 갖는다.  이며 가정에 의하여
이며 가정에 의하여  인
인  가 존재하므로 최솟값은
가 존재하므로 최솟값은  나
나  가 될 수 없다. 즉,
가 될 수 없다. 즉,  에서 최솟값을 가져야 한다.
에서 최솟값을 가져야 한다.  에서 최솟값을 가진다고 하면 일계도함수판정법에 의하여
에서 최솟값을 가진다고 하면 일계도함수판정법에 의하여  이다.
이다.
12세기 인도 천문학자 바스카라 2세(Bhāskara II)가 처음 서술하였다고 한다. 형식적인 증명은 미셸 롤(Michel Rolle)이 1691년에 미적분학을 이용하여 처음 증명하였다.
"롤의 정리"라는 이름은 1834년 독일의 M.W.Drobisch와 1846년 이탈리아의 Giusto Bellavitis가 처음 썼다고 한다.
같이 보기[편집]
참고 문헌[편집]
- James Stewart (2009년). 《Calculus(Metric International Version, 6th Edition)》. Brooks/Cole, Cengage Learning. ISBN 0-495-38362-7.





![{\displaystyle \left[a,b\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f30926fb280a9fdf66fd931e14d4363cb824feaa)










