0.999…

수학에서 순환소수인 0.999…는 소수점 뒤로 9가 무한히 반복되는 소수로, 실수 1의 또 다른 십진법 소수 표현이다. 즉 "0.999…"와 "1"은 같은 수이다. 이러한 증명은 실수론의 전개, 배경이 있는 가정, 역사적 맥락, 대상이 되는 청자(듣는 사람) 등에 맞는 수준에 따른 것으로서 여러 단계의 수학적 엄밀함을 적절하게 고려한 다양한 정식화가 있다.
0.999...는 줄임표 앞의 9의 개수를 다소 늘리거나 줄여서 0.99999…처럼 쓰기도 한다. 또는 순환마디를 명확하게 하기 위해 또는 와 같이 표기하기도 한다. 일반적으로 임의의 0이 아닌 유한소수(말미에 무한개의 0을 붙여서 무한소수로 봄)는 소수 부분이 있는 자리부터 9가 연속해서 반복되는 소수 표시(예를 들어 8.32, 8.31999…)를 가진다. 보통은 유한소수 표시를 선호하는 것으로서 그것이 하나의 뜻만 가진 표시라는 오해로 이어지기 쉽다. 이와 같은 현상은 임의의 다른 밑에 관한 위치 기수법이나 같은 실수의 표기법에서도 발생한다.
0.999…와 1의 등가성은 실수의 체계(해석학에서 가장 일반적으로 이용되는 체계)에 0이 아닌 무한소가 존재하지 않는 것과 깊이 관련되어 있다. 한편 초실수의 체계와 같이 0이 아닌 무한소를 포함한 다른 수 체계도 있다. 그런 체계의 대부분은 표준 해석에 따른 등식에서 0.999…의 값은 1과 같아지지만 일부 체계에서는 기호 "0.999…"에 다른 해석을 주면서 1보다 무한소만 작도록 만들 수 있다.
등식 0.999… = 1은 수학자들에게 오랫동안 받아들여져 일반적인 수학 교육의 일부였음에도 불구하고 이를 충분히 직관에 반하는 것으로 간주하고 의심하거나 거부 반응을 보이는 일부 학생들이 있다. 이와 같은 회의론은 이러한 등식을 그들에게 납득시키는 것이 얼마나 어려운가가 수학 교육의 여러 연구 주제가 되는 것에 정당성을 부여하는 정도로 당연하게 존재한다.
대수적인 증명[편집]
0.999…라는 실수를 명확히 파악하려면 소수점 이하의 자리가 모두 9임을 이용해야 한다. 위치 기수법으로 표시된 유한소수의 "자리별 사칙연산"을 무한소수에 대해서도 적용할 수 있다고 간주하면 0.999… = 1을 초등적으로 이끌어 낼 수 있다.
분수를 통한 증명[편집]
13을 소수로 표시하면 소수점 이하의 자리가 모두 3이라는 것을 이용한다. 13은 1 ÷ 3이 되는데 장제법을 취하면 순환소수 0.333…이 된다. 여기서 3은 무한히 계속된다. 이러한 소수점 이하에 있는 각각의 자리는 3배나 되는데 모두 9에서 유한소수일 때와 마찬가지로 각각의 자리에 대한 곱셈을 한꺼번에 할 수 있다고 가정한다면 무한소수 0.333…의 3배인 0.999…와 같은 값이 나온다. 또한 13 × 3 = 1이 나오는데 0.999… = 1이 된다.[내용주 1] 이와는 별도로 19 = 0.111…이라는 등식의 양 쪽에 9를 곱해서 증명하기도 한다.
위치 기수법의 성질을 이용한 증명[편집]
십진법에 따라 표시된 유한소수에 10을 곱하면 숫자는 변하지 않고 소수점이 오른쪽으로 이동한다. 이것이 무한소수에 대해서도 성립된다고 간주하면 0.999… × 10 = 9.999…가 되는데 이는 원래의 수에 비해 9 정도 큰 편이다. 자리마다 뺄셈을 취급할 수 있는 것이 무한소수에 대해서도 성립된다고 간주하면 9.999…- 0.999…= 9.000…이 된다. 그런데 소수점 이하로 무수히 이어지는 0은 수를 변화시키지 않기 때문에 이 차이는 바로 9와 같다. 문제의 소수인 0.999…를 c라고 가정하면 10c - c = 9이 되는데 이러한 방정식을 풀면 c = 1이라는 값을 얻을 수 있고 증명이 완료된다.[내용주 1] 즉 다음과 같은 등식이 나온다.
이러한 위치 기수법의 성질을 이용한 증명은 다른 유한소수(0.25와 0.24999… 등)에도 적용이 가능하다.
무수한 자릿수 조작의 정당성[편집]
위에서 언급한 2개의 증명에서 이용한 무수한 자릿수 조작(즉 곱셈이나 뺄셈)을 일제히 실시하는(즉 ... 부분에 행한다) 것은 엄밀성이 결여된 것이기 때문에 그러한 정당성이 명확하지 않다. 이 과정은 유한소수에 관해서 실수의 계산 법칙에만 의존하고 있다. 이러한 조작이 무한소수에도 적용될 수 있음을 증명하기 위해서는 해석적인 증명 문단에서 언급하는 실제 해석 기법을 필요로 한다.
해석적인 증명[편집]
0.999…라는 소수점 이하의 자리에 무수한 9를 더한다는 정의 자체가 해석적이다. 이것을 1과 같다는 것을 엄밀하게 증명하기 위해서는 실해석학에 따른 방법을 필요로 한다. 0.999…라는 무한소수를 정확히 파악하기 위해서는 소수 부분의 자리가 무수히 나열되어 있는 것을 명확하게 다시 정의하는 것이 필요하다.
차이에 주목한 증명[편집]
0.999…가 1과 같다는 것을 증명하기 위해서는 그것들의 차이가 0임을 증명하면 된다. 그만큼 무수히 나열된 9에 대한 정의는 희미하지만 초등적이고 해석적으로 이끌 수 있다.
(증명)
또한 이 증명에서는 마지막으로
인 것을 증명 없이 이용하고 있다.
이것을 증명하기 위해서는 실제 해석에 있어서의 실수의 완비성(아르키메데스 성질)이 필요하다.
무수한 자리에 대한 정의의 재고[편집]
0.999…, 일반적으로는 무한소수(소수점 이하에 무수한 자리가 나열된 실수)에 대한 명확한 정의를 다시 논의하기 위해 정식화한다. 0.999…를 생각하는데 정수 부분은 1자리만 생각하면 충분하고 음수는 생각하지 않아도 되므로 고찰해야 하는 소수 표시는
형태가 된다. 소수 부분은 정수 부분과 달리 유한한 자릿수로 제한되지 않는다. 이는 기수 10에 따른 위치 기수법이기 때문이다. 예를 들어 a1의 단위가 a2의 10배이면 a3의 단위는 a2의 110배가 된다.
급수의 계산[편집]
소수 전개의 일반적인 정의로는 아마도 급수(무한한 수열의 총합)로 정의하는 것이다. 즉
로 나타낸다.
여기에서 0.999…의 소수 부분의 계산에는 등비 급수의 공식 여기에서 0.999…의 소수 부분 계산에는 등비급수에 따른 수열의 공식[1]
- |r| < 1일 때
을 적용할 수 있다.
0.999…는 위에서 언급한 왼쪽 부분에서 첫 부분을 a = 910, 공비를 r = 110이라고 정의했기 때문에 이 공식보다
라고 쉽게 문제를 해결할 수 있다. 이 증명은 1770년경에 스위스의 수학자인 레온하르트 오일러가 집필한 《대수학 원론》(실제로는 9.999… = 10이라고 증명했음)에서 나타난다.[2]
등비급수의 공식 자체는 오일러 이전의 성과이지만 18세기까지는 그 도출이 모두 항별 연산의 증명 없이 이루어졌다. 1811년이 되어서야 보니캐슬(Bonnycastle)의 교과서 《대수학 소개》(An Introduction to Algebra)에서 등비급수에 관한 논의가 시작되었는데 이는 0.999…에 관한 항별 조작을 정당화하고 있다.[3]
19세기에는 지금까지의 너무 자유로운 무한한 합의 계산에 대한 반동으로서 "급수는 그 부분합의 극한으로서 정의된다."라는 현재의 수학에서도 이용되고 있는 정의가 만들어졌다. 현대의 증명에 근거한 미적분학이나 해석학의 입문서에서는 이와 관련된 정리를 증명하고 있으며 이러한 등비급수를 명확하게 계산하고 있다.[4]
수열 {xn}에서 번호 n을 끝없이 나아가게 하면 거리 |xn − x|가 0에 접근할 때 수열 {xn}의 극한은 x라고 정의한다. 등식 0.999… = 1 자신은 다음과 같이 극한을 나타내면서 증명한다.
마지막 등호 ()는 실수의 완비성 가운데 하나인 아르키메데스 성질을 사용하여 증명된다. 이러한 극한을 바탕으로 0.999…의 설명은 종종 알기 쉽지만 부정확한 용어로 구성되어 있음을 입증한다. 예를 들어 1846년에 출간된 교과서 《대학교 산술》(The University Arithmetic)에서는 "0.999…로 무한히 이어지는 수는 1이다. 왜냐하면 9를 축적할 때마다 그 값은 1에 가까워지기 때문이다."라고 설명하고 있으며 1895년에 출간된 《학교 산수》(Arithmetic for Schools)에서는 "9를 충분히 이용하면 0.999…와 1 간의 거리는 놀랄 만큼 작은 값이다."라고 설명하고 있다.[6] 직관에 의존하지 않고 뚜렷한 이해를 얻기 위해서 오귀스탱 루이 코시나 베르나르트 볼차노의 미적분을 엄밀한 이론으로 재구축하는 흐름이 나타났다. 1860년대에 카를 바이어슈트라스에 의해 엡실론-델타 논법이 고안되어 무한한 개념을 부등식의 임의성에 치환함으로써 항별 조작 가능성 등에 대해서도 설명이 뒤따르게 된다.
구간 축소법과 상한[편집]
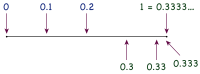
무한소수의 소수 부분을 급수로 직접 계산하는 방식의 도출에 대해서 이와는 별도로 또 하나의 방법은 무한소수가 취하지 않은 값의 범위를 배제하는 방법이다.
실수 x는 닫힌 구간 [0, 10](즉 0 이상 10 이하)에 속하며 이 구간 [0, 10]에서 한 자리마다 10개 구간 [0, 1], [1, 2], [2, 3], …, [9, 10]으로 분할(끝점에서만 겹침)한다. 실수 x는 적어도 1개에 속하며 그 구간의 하한, 예를 들어 x가 구간 [1, 2]에 속할 때에는 "1"을 기록한다. 다음에 속한 구간 [1, 2]를 소수 한 자리마다 [1, 1.1], [1.1, 1.2], …, [1.8, 1.9], [1.9, 2]로 분할하고 x가 속한 구간의 하한을 기록하는 조작을 반복하면 a0, a1, a2, a3, …에서 정해지는 구간의 감소 줄이 만들어진다. 이 수열은
라고 표현한다.
이러한 기록 방법에 따라 실수 1은 처음에 [0, 1]에 속하거나 아니면 [1, 2]에 속하는가에 따라 1 = 1.000...와 1 = 0.999…)의 2가지 표시를 얻을 수 있게 된다. 각각의 소수 기록 표시가 나타내는 실수가 동일한 것을 증명하려면 직접적으로는 극한을 사용하여 이루어지지만 순서의 논의를 계속 다른 구성 방법도 있다.[7]
직접적인 방법으로는 구간 축소법이 꼽힌다. 이 원리에 따르면 닫힌 구간의 감소열이 주어지고 그 폭이 0으로 수렴할 때, 그러한 구간의 교집합은 단지 하나의 실수로 이루어진 1점 집합인 것이 실수의 완비성으로 증명된다. 따라서 x = a0.a1a2a3…는 [a0, a0 + 1], [a0.a1, a0.a1 + 0.1], …의 모두에 속하는 유일한 실수라고 정의한다. 따라서 0.999…는 [0, 1], [0.9, 1], [0.99, 1], …의 모든 것에 속하는 유일한 실수가 된다. 반면 실수 1은 이들 모든 구간에 속하기 때문에 0.999… = 1이 된다.[8]
구간 축소법은 실수의 완비성 중에서 보다 직관적이라고 생각되는 상한의 존재에 근거하고 있다. 이 사실을 직접 사용하면 a0.a1a2a3…을 근사값의 집합 a0, a0.a1, a0.a1a2, …}의 상한으로서 정의할 수 있다.[9] 증가열 상한의 존재 정리는 실수의 연속성으로서 구간 축소법과 같은 값임을 나타낼 수 있으므로 다시 0.999… = 1을 얻게 된다. 톰 어포스톨은 다음과 같은 결론을 내렸다.[10]
실수가 다른 2개의 소수 표시를 가질 가능성이 있다는 사실은 단순히 실수로 이루어진 서로 다른 2개의 집합의 상한, 하한이 같아질 가능성이 있다는 사실의 반증에 불과하다.
실수의 구성[편집]
공리적 집합론을 이용하여 실수의 집합을 유리수의 집합을 통해 조립된 어떠한 종류의 구조로서 명시적으로 정의하는 방법은 여러 가지가 존재한다. 먼저 자연수란 물건을 셀 때 사용하는 번호를 말하며 0부터 시작하여 0, 1, 2, …과 +1씩 더하면서 얻을 수 있다. 자연수를 확장해서 정수 전체를 얻으려면 각 자연수의 반수를 첨가하면 된다. 또한 그러한 몫을 첨가하면 유리수 전체를 얻을 수 있다. 이들 수 체계에는 덧셈, 뺄셈, 곱셈, 나눗셈이라는 사칙연산과 관련되어 있으며 또한 임의의 2가지 수를 비교한 대소 관계(어느 쪽이 큰지, 작은지, 동일한지)라는 순서도 갖추고 있다.
유리수에서 실수로의 확장은(자연수에서 정수나 유리수로의 확장과 비교해서) 큰 비약이다. 이러한 확장 방법은 적어도 2가지 수법이 잘 알려져 있는데 둘 다 1872년에 발표된 유리수의 절단(데데킨트 절단)에 의한 것과 코시 열에 의한 것이다. 이러한 실수 구성법에 따라 0.999… = 1을 증명하고 있는 실제 해석 교과서는 볼 수 없다. 현대 수학에서는 해석학적으로 실수를 구성하고 그것이 수의 공리를 충족시키는 지에 주의를 기울인다. 공리에 의한 해석적 기법에 의해 0.999… = 1을 증명하게 되기 때문이다. 그러나 실수의 구성을 보다 적절하게 논리적으로 실시함으로써 0.999… = 1의 증명은 더 직접적으로 이루어진다(self-contained)라고 주장하는 사람도 있다.[내용주 2]
데데킨트 절단에 따른 구성[편집]
데데킨트 절단의 접근 방법에서 임의의 실수 x는 "x보다 작은 유리수 전체로 이루어진 무한 집합"으로 정의한다.[내용주 3] 이러한 사고 방식에서 실수 1은 "1보다 작은 모든 유리수의 집합"이 된다.[11]
정수에서의 데데킨트 절단은 소수 전개를 통해 얻을 수 있다. 소수 표시를 적당한 자리까지 잘라서 얻을 수 있는 유리수를 사용하고 그보다 작은 유리수 전체의 합집합을 만들면 되는 것이다. 이러한 방법으로 실수 0.999…라는 것이 무엇일까를 생각한다면 r < 0, r < 0.9, r < 0.99, … (즉 어떤 자연수 n에 대하여 r < 1 - (110)n을 충족시키는 모든 유리수 r이 만드는 집합)로서 정의한다고 하는 것이 된다.[12] 0.999…보다 작은 모든 유리수는 1보다 작기 때문에 이것은 실수 1의 바탕에 포함된다. 한편 실수 1의 바탕이 되는 임의의 유리수
(b ≥ 1)를 생각하면
이 되기 때문에, ab는 0.999…의 바탕이 된다. 따라서 0.999…와 1은 모두 똑같은 유리수를 바탕으로 하기 때문에 이들은 집합으로서 같다. 즉 0.999… = 1이라는 등식이 성립하는 것이다.
데데킨트 절단에 따른 실수의 정의는 1872년에 리하르트 데데킨트에 의해 처음 발표되었다.[13] 위에서 언급한 실수를 각각의 소수 전개로 귀착시키는 방법은 프레드 리치먼(Fred Richman)이 수학 잡지 《매서매틱스 매거진》(Mathematics Magazine)에 게재한 〈Is 0.999…= 1?〉이라는 해설 논문에 의한 설명이다. 이 논문은 해당 대학의 수학 교사와 학생들을 위해 집필했다.[14] 리치먼은 임의적이고 조밀한 유리수의 부분 집합에서의 절단을 생각해도 같은 결과를 가져오는 것을 지적하고 있다. 리치먼은 그 중에서도 분모가 10의 거듭제곱인 분수 전체를 이루는 조밀한 부분 집합을 이용해서 0.999… = 1의 증명을 보다 직접적으로 전달했다. 또한 x < 1이 되는 x는 절단을 갖고 있으나 x ≤ 1이 되는 x는 절단을 갖지 않는 것도 지적하면서 "이는 0.999…와 1이 달라지는 것을 배제하는 것이다. 실수의 전통적인 정의 안에서 등식 0.999… = 1은 처음부터 포함되어 있다."는 결론을 내렸다.[15] 리치먼은 이러한 절차를 수정함으로써 0.999… ≠ 1이라는 다른 구조를 이끌어냈다.
코시 열에 따른 구성[편집]
실수를 구성하는 또 다른 방법은 실수의 절단에 비하면 간접적으로나마 역시 유리수의 순서를 이용하는 것이다. 먼저, 2개의 유리수 x와 y에 대해, 거리 d(x, y)를 절댓값 |x - y|로 정의한다(z의 절댓값 |z|란 z와 -z의 작지 않은 편으로 정의하는데 음수가 아니다). 즉 실수 전체를 이러한 거리 d에 관한 유리수의 코시 열 전체를 다음과 같이 정의하는 동치류로 나눈 것으로서 정의하는 것이다(실수의 완비성도 참고할 것). 여기서 유리수열(즉 자연수에서 유리수로의 함수) xn}이 코시 열인 경우에는
- 임의의 정의 수 ε에 대해 번호 N이 존재하며 N보다 큰 모든 m, n에 대해 |xm − xn| < ε
가 성립되는(즉 번호가 충분히 앞이면 인접한 2항 간의 거리가 끝없이 작아진다) 것으로 정의된다.[16]
2개의 코시 열 xn}과 yn}는 동치임을 정의하기 위하여 xn - yn을 0으로 수렴한다. 소수 a0.a1a2a3…에 대하여 각 자리 이후를 차례로 버림으로써 얻을 수 있는 수열은 유리수의 코시 열을 정하므로 이러한 코시열이 이러한 소수의 전개가 나타내고 있는 실수의 참값으로 정해지게 된다.[17]
이러한 성질보다 0.999… = 1을 증명하기 위해서 해야 할 것은 유리수의 코시 열인데
이 같은 값이 된다. 즉
가 0으로 수렴되는 것을 증명하는 것이다.
이 극한은 단순하고[18] 수열의 극한에 대한 정의로 나타난다. 이는 0.999… = 1이라는 공식을 나타낸다.
코시 열에 의한 실수의 정의는 모두 1872년에 에두아르트 하이네와 게오르크 칸토어에 의해 최초로 독립적으로 발표되었다.[13] 0.999 … =1의 증명을 포함한 소수 전개에 의한 접근 방식은 1970년에 그리피스(Griffiths)와 힐턴(Hilton)이 집필한 교과서 《고전 수학에 관한 종합 교과서: 현대적 해석》(A comprehensive textbook of classical mathematics: A contemporary interpretation)을 따르고 있다. 이 교과서는 잘 알려진 개념에 대해 현대의 관점에서 재검토하는 것을 중점적으로 다루고 있다.[19]
다른 수 체계에서의 행동[편집]
실수는 표준적인 수 체계이지만 사람들은 "0.999…"라는 무수 자리의 표기가 있는 실수를 나타낼 것이라고 자연스럽게 생각한다. 윌리엄 티머시 가워스는 자신의 저서인 《수학: 매우 짧은 소개》(Mathematics: A Very Short Introduction)에서 등식 0.999 … = 1을 결론 짓는 것 역시 "관습"이라고 설명하고 있다. 즉
"하지만 그것은 결코 자의적인 관습이 아니다. 왜냐하면 그것을 받아들이지 않으면 색다른 새로운 대상을 발견하거나 또는 산술이 잘 알려진 규칙 몇 가지를 포기하거나 둘 중 하나가 강제되기 때문이다.[20]
표준적인 수 체계인 실수체에 대해 일반적인 경우와 다른 방법으로 수를 구성하고 0.999…라는 표기가 의미를 가지는 실수와는 다른 수 체계를 정의할 수 있다. 그러한 수 체계에 있어서는 본 항 첫머리 부근의 문단에서 언급한 증명 등은 그러한 체계에 있어서의 기술로서 다시 해석하지 않으면 안 된다. 또한 그러한 체계에 있어서(위에서 언급한 증명이 올바르다고 하는 근거를 잃거나 잘못이라고 나타내거나 해서) 0.999…와 1이 동일한 대상을 나타내는 것이 아닐 가능성이 발견되기도 한다. 그렇다고 하더라도 많은 수 체계는 (실수의 체계를 대체하는 독립된 대상으로서가 아니라) 실수의 체계가 확장되는 것이며 고로 거기서는 0.999… = 1도 계속 성립하게 된다.
그러나 그러한 체계에 있어서조차 "0.999…"라고 표시되는 수가 의미를 가지는 경우에는) 0.999…가 어떻게 행동하는가 하는 것만이 아니라 관련된 현상의 행동에 대해서 생각하기 위해 이를 대체하는 수 체계를 고찰하는 것은 의미 있는 것이라고 할 수 있다. 즉 어떤 현상이 실수 체계에 있어서의 경우와는 다른 행동을 한다면 그러한 체계에 포함된 전제 조건은 실수 체계의 그것의 적어도 하나를 망가뜨린 것이 되어야 한다(다음과 같이 제시하는 체계가 실수에 있어서의 어떠한 현상이나 조건을 부정하는가 하는 관점에 서서 설명할 수 있다).
무한소를 포함한 체계[편집]
0.999… = 1의 몇 가지 증명은 일반적인 실수가 아르키메데스 전순서군이라는 것, 즉 "0이 아닌 무한소는 존재하지 않는다."라는 것에 의존하고 있다. 특히 차이가 1 - 0.999…는 임의의 바른 유리수보다도 작을 것이므로 그것은 (0이) 무한소여야 하지만 실수 체계에서는 0이 아닌 무한소는 없기 때문에 차이는 0, 즉 2개의 값은 동일한 것으로 결론이 난다. 그래도 실수의 비아르키메데스적인 대체가 될 수 있는 여러 가지 체계를 포함한 수학적으로 일관된 순서 대수계가 존재한다.
초실수[편집]
비표준 해석학에 의해 무한소(및 그 역수)의 완전한 계열을 포함한 수체계가 제공되는[내용주 4] A. H. 라이트스톤(A. H. Lightstone)은 구간 (0, 1)∗에 속하는 초실수(hyperreal number)에 대한 소수 전개를 생각했다.[21] 라이트스톤은 확장 실수에 초자연수로 첨자된 숫자열
이 대응하는 것을 지적했다. 여기서 세미콜론의 왼쪽은 유한(표준) 자연수 자리를 나타내고 세미콜론의 오른쪽은 무한대(비표준) 자연수 자리를 나타낸다. 여기서 세미콜론 직전이나 직후 자리와 같은 것은 존재하지 않는다는 점에 주의해야 한다. 라이트스톤은 0.999…에 대해 직접 취급한 것이 아니라 이행 원리의 귀결로서 실수 1⁄3가 0.333…;…333…으로 나타난다는 점을 지적했다. 고로 0.999…;…999… = 1이다. 여기에서 말하는 의미에서의 소수 전개가 반드시 수를 나타낸다고는 할 수 없다는 것에 주의해야 한다. 특히 "0.333...; 000..."나 "0.999…; 000..."는 아무런 수와도 대응하지 않는다. 이 사실은 넘침 원리를 사용해 설명할 수 있다. 소수 전개의 각 자릿수는 맵핑 으로 간주한다. 유한한 자릿수가 모두 3이라고 가정한다. 즉
이다. 여기에 넘침 원리를 적용하면 어떠한 무한대 초자연수 이 있고
이 성립된다. 즉 는 "0.333…;…333000…"이나 "0.333…;…333001854…"처럼 어느 무한대 자릿수까지 3이 연속하는 초실수여야 한다. 이 사실은 다음과 같이 기술할 수도 있다. 초실수체는 순서체이기 때문에 순서위상을 생각할 수 있지만 (초)실수의 가산열 는 수렴하지 않기 때문에 표준 자리만 딱 9인 것과 같은 초실수는 그러한 유한 소수 표시의 위상적 극한이라고 간주한다고 해도 여전히 존재하지 않는다.
수 0.999…의 표준적인 정의는 0.9, 0.99, 0.999, …가 되는 수열의 극한이지만 그것과 다른 정의로서 테런스 타오가 초극한(ultralimit)이라고 명명한 수열 0.9, 0.99, 0.999, …의 초거듭제곱 구성에 관한 동치류 [(0.9, 0.99, 0.999, …)]는 1보다 무한소만 작다. 보다 일반적으로 층수 H의 무한대 초자연수의 위치에 마지막 9가 오는 초실수 uH = 0.999…;…999000…,는 보다 엄밀한 부등식 uH < 1을 만족한다. 이에 따라 "무한개의 9의 뒤에 0이 계속된다."는 것의 다른 해석을
라고 이해할 수 있다. 이렇게 해석한 "0.999…"는 1에 무한히 가깝다. 이언 스튜어트는 이러한 해석을 "0.999…는 1보다 "아주 조금 작다."라는 직관을 엄밀하게 정당화하는 "완전히 합리적인" 방법으로 특징지었다.[23]R. Ely (2010) 역시 학생들이 가진 0.999… < 1이라는 생각을 실수에 대한 잘못된 직관으로 보는 가정에 의문을 제기하며 오히려 그것을 '비표준적'인 직관으로 해석하는 편이 해석학의 습득에 있어서 가치가 있는 것이 아닐까하고 생각했다. 조제 베나데트(Jose Benardete)는 자신의 저서인 《무한대: 형이상학에서의 에세이》(Infinity : An essay in metaphysics)에서 지나치게 제한된 수 체계로 이야기를 한정하면 수학 이전의 자연적인 직관의 일부는 표현할 수 없다고 주장했다.
The intelligibility of the continuum has been found—many times over—to require that the domain of real numbers be enlarged to include infinitesimals. This enlarged domain may be styled the domain of continuum numbers. It will now be evident that .9999⋯ does not equal 1 but falls infinitesimally short of it. I think that .9999⋯ should indeed be admitted as a number ⋯ though not as a real number.[24] (해석: 연속체의 명확한 이해를 위해서는 실수의 영역을 무한소를 포함하도록 확대하는 것이 필요하다는 의견을 "여러차례 반복하여" 찾아냈다. 이러한 확대된 영역은 연속체 수 영역의 형태를 취할 것이다. 이제 0.9999…가 1과 같지는 않고 그보다 무한소만 작음이 분명하다. 나는 0.9999…가 실제로 "실수"는 아니지만 하나의 "수"로서 허용되어야 한다고 생각한다.)
초현실수와 조합론적 게임 이론[편집]
전항과 특별히 관련하여 조합론적 게임 이론에 있어서 같은 실수 대체 체계로서 "무한 2색 해큰부시 게임"(infinite Blue-Red Hackenbush)을 생각할 수 있다. 엘윈 벌캠프(Elwyn Berlekamp)는 1974년에 데이터 압축 아이디어에 자극을 받아서 해큰부시 문자열과 실수의 이진법 전개 관계에 대해 언급했다. 예를 들어 "해큰부시 문자열"(Hackenbush string) LRRLRL…의 값은 0.010101…2 = 13이 된다. 그러나 문자열 LRLLL… (0.111…에 대응한다)의 값은 1에 비해 극히 약간 작다. 이들의 2가지 수(LRLLL…과 1)의 차이는 초현실수 1ω (ω는 최소 무한 순서수)이다. 이와 관련된 게임은 LRRRR... 즉 0.000…2이다.[내용주 5]
뺄셈의 재고[편집]
다른 방법은 뺄셈은 아무 때나 할 수 있는 게 아니라 "1 - 0.999…는 존재하지 않는다."고 판단해서 버리는 것이다. 덧셈을 갖고 있지만 뺄셈이 갖고 있지 않은 수학적 구조에는 교환법칙 반군, 교환법칙 모노이드, 반환 등이 포함된다. 리치먼은 0.999… < 1이 되도록 디자인된 그러한 2가지 구조를 생각하였다.
먼저 리치먼은 음수가 아닌 "십진수"를 문자 그대로 소수 전개가 되도록 정의하는 한편 사전식 순서라는 덧셈을 정의했다. 여기서는 0.999… < 1임에 주의한다. 왜냐하면 단순히 하나의 자리에 있어서 0 < 1이 되기 때문이다.그러나 어떤 "무한소수" x에 대해서도 0.999… + x = 1 + x이 된다. 이에 "십진수"에 대한 특징적인 사항으로 하나는 덧셈이 반드시 타결이 되지 않는다는 점이고 다른 하나는 13에 대응하는 "십진수"가 존재하지 않는다는 점이다. 곱셈을 정의하면 "십진수"는 올바른 값에 대한 모든 순서 교환 반환을 이룬다.[25]
리치먼은 곱셈을 정의할 때에 "절단 D"(cut D)라고 부르는 다른 구조를 정의했는데 이는 소수의 절단 집합이다. 일반적인 이 정의는 실수를 이끌지만 리치먼은 d에 대하여 절단 (&-∞, d)과 "일반적인 절단" (&-∞, d] 양쪽을 허용했다. 그 결과 실수들은 소수와 불안정한 상태로 공존(living uneasily together with)하게 된다. 따라서 다시 0.999… < 1을 얻게 된다. "절단 D"에는 올바른 무한소는 존재하지 않으나 "일종의 음수 무한소" 0−가 존재한다. 0−에는 소수 전개가 존재하지 않는다. 리치먼은 0.999… = 1+0 -로 결론을 내렸으나 방정식 "0.999… + x = 1"에 대한 해를 결정하지 않았다.[내용주 6]
p진수[편집]
1 - 0.999…는 무엇이 될 것인가를 물으면 종종 "0.000...1"을 떠올리게 되는 경우가 있다. 여기에 의미를 가질 수 있는지 없는지를 떠나 0.999…의 "마지막 9"에 1을 더함으로써 차례대로 올라가고 모든 9가 0으로 바뀌어서 1번째로 1이 남겠다는 의도는 직관적으로는 명백하다. 이 생각은 (다른 이유가 있지만) 0.999…에는 "최후의 9"가 없기 때문에 부당하지만[26] "최후의 9"를 갖는 무한 문자열을 가지는 체계라고 하는 것은 존재한다.
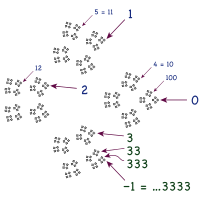
p진수는 정수론이 연구 대상으로 하는 수체계이다. 실수와 똑같이 p진수는 코시 열을 경유해서 유리수의 완비화로 만들 수 있다. 단 이 구성에는 0은 1보다도 p에 가깝고 pn에는 더욱 가깝다는(실수 구성 때와는) 다른 거리를 이용한다. p진수는 p가 소수일 때 체를 이루어 p가 소수가 아닐 때(10은 이러한 경우이다)에도 환을 이룬다. 따라서 p진수에 덧셈이나 곱셈과 같은 계산을 실행할 수 있으며 무한소는 존재하지 않는다.
p진수에는 소수 전개와 비슷함을 생각할 수 있는데 자리가 왼쪽으로 갈 수록 실수의 소수 전개와는 반대로 오른쪽으로는 유한한 자리만 진행한다. 10진 전개의 경우에는 …999를 생각한다. 한 자리에 1을 더할 수 있는데 0만 남겨두고 반올림이 계속된다. 그 결과 1 + … 999 = … 000 = 0 등식이 성립되고 …999 = -1이 된다.[27] 또 하나의 도출 방법은 등비급수를 이용한다. "…999"의 의미를 가진 등비급수는 실수에 있어서는 수렴하지 않으나 10진수로는 수렴하여 잘 알려진 공식을 다시 사용할 수 있고
이라는 등식이 성립된다(앞의 등비급수와 비교하라). 3번째 도출 방법은 중학교 1학년생에 의해 고안되었다. 이 학생은 교사가 0.999… =1을 극한으로 정의한 논의에 의문을 가졌으나, 위에서 언급한 10을 곱하는 증명을 반대 방향으로 이용해 보려고 했다. 따라서 x= …99은 10 x = … 990이므로 10x = x - 9이 되고 다시 x = -1이 된다.[27]
실수의 '이중십진' 표기[편집]
실수의 '이중십진' 표기에서는 소수점의 양쪽 모두에서 무한한 숫자열을 허용한다. (단 왼쪽의 숫자열은 결국 순환해야 한다.) p진수에서 참이지만 실수의 십진법 표기에서 참이 아닌 등식 …999 = -1와 p진수에서 거짓이지만 실수의 십진법 표기에서 참인 등식 0.999… = 1은 이중십진 표기에서는 모두 참이다. 2개의 등식 양쪽을 더해서 …999.999… = 0을 얻을 수 있다.[29]
일반화[편집]
등식 0.999… = 1의 증명은 즉시 2가지 방법으로 일반화된다. 1번째로 바로 그 특별한 경우에 있어서 생각된 것처럼 0이 아닌 모든 유한소수(즉 뒤에 0이 끝없이 반복된다)는 9가 뒤에서 계속 이어지는 다른 표현을 갖고 있다. 예를 들어 0.24999…는 0.25와 같다.[30]
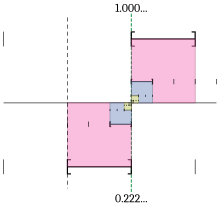
2번째로 0.999… = 1에 상당하는 결과를 다른 기수에도 적용할 수 있다. 예를 들어 이진법에서는 0.111… = 1이며 삼진법에서는 0.222… = 1이다. 일반적으로 기수를 b로 할 때 소수점 이하는 b - 1이 반복되어 늘어선다. 실해석학 교과서에서는 0.999… = 1의 예를 건너뛰고 이러한 일반화 가운데 한 쪽 또는 양 쪽을 처음부터 소개하는 경향이 있다.[31]
1의 다른 표현은 비정수를 기수로 하는 경우에도 나타난다. 예를 들어 황금비를 기수라고 한다면 2개의 표준적 표시는 1.000…과 0.101010…이지만 그 밖에도 0.11, 0.1011, 0.101011과 같이 인접한 "1"을 포함한 무수한 표현이 있다. 일반적으로 1과 2 사이에 있는 거의 모든 q에 대해 "비가산 무한"인 "1의 q진 표현"이 존재한다. 한편 (1보다 큰 자연수를 포함한) 또 다른 "비가산 무한"인 q가 1의 q진 표현(자명한 1.000…을 제외함)은 단 하나 밖에 없다. 이 결과는 1990년경에 에르되시 팔(Erdős Pál), 호르바트 미클로시(Horváth Miklos), 요 이슈트반(Joó István)이 최초로 언급했다. 1998년에는 코모르니크 빌모시(Komornik Vilmos)와 파올라 로레티(Paola Loreti)가 이러한 최소 기수로 q = 1.787231650…를 결정했다. 이 기수에 있어서는 1 = 0.11010011001011010010110011010011…인데 이 수는 순환이 되지 않는 투에-모스 수열을 부여한다.[32]
더욱이 변칙적인 규칙에 근거한 기수법(the most general positional numeral systems)에 있어서도 0.999 = 1에 상당하는 결과를 얻을 수 있다. 이들 또한 다양한 표현을 갖고 있기 때문에 어떤 의미에서는 다루기가 더욱 어렵다. 예를 들어[33]
- 평형삼진법(balanced ternary system)에 있어서는 12 = 0.111… = 1.111…라고 표현한다.
- 계승진법(factoradic system)에 있어서는 1 = 1.000… = 0.1234…라고 표현한다.
마르코 페트코브셰크(Marko Petkovšek)는 이와 같은 하나의 수를 복수의 방법으로 나타낼 수 있다고 하는 것은 위치 기수법을 이용하는 것의 필연적인 결과라고 말하면서 모든 실수를 취급하는 임의의 위치 기수법에서 복수의 표현을 갖는 실수의 집합이 항상 조밀함을 증명했다. 그는 이러한 증명을 "일반 위상 공간에 관한 교육적인 초급 연습 문제"라고 불렀다. 이는 위치 기수법에 따른 값의 집합을 스톤 공간으로 판단하고 이러한 실수 표현이 연속 함수에 의해 주어진다는 것을 증명하고 있기 때문이다.[34]
응용 사례[편집]
1의 다른 표현으로서의 0.999…에 대한 하나의 응용을 초등 정수론에서 볼 수 있다. H. 굿윈(H. Goodwin)은 1802년에 어떤 종류의 소수를 분모로 하는 분수에서는 순환 소수로 표시했을 때 9가 나타나는 것을 발표했다. 예를 들면
- 17 = 0.142857142857…, 142 + 857 = 999
- 173 = 0.0136986301369863…, 0136 + 9863 = 9999
라고 적혀 있다.
E. 미디(E. Midy)는 1836년에 이러한 분수에 관한 일반적인 결과를 증명했는데 현재는 미디의 정리라고 부르고 있다. 이 논문은 모호한 편이고 그의 증명이 직접 0.999…를 포함하는 지의 여부는 알 수 없다. 그러나 W. G. 리빗(W. G. Leavitt)이 제시한 적어도 하나 정도의 현대적인 증명에서는 포함되고 있다. 만약 0.b1b2b3… 형식의 소수가 양의 정수임을 증명하면 그것은 0.999…나 다름이 없는데 이는 이러한 정리에서 9들이 출현하는 원인이 된다.[35] 이러한 방향에 대한 연구는 최대공약수, 모듈러 산술, 페르마 소수, 군의 원래 위수, 이차 상호 법칙 등의 개념에 동기를 부여하고 있다.[36]

실해석학에서는 삼진법에서 유사한 표현인 0.222… = 1은 가장 단순한 프랙탈 가운데 하나인 칸토어 삼진 집합(the middle-thirds Cantor set)의 특징을 부여하는 데에 중요한 역할을 하고 있다.
- 단위 구간 [0, 1]의 점은 삼진법으로 0과 2만으로 표현하는 경우에 한하여 칸토어 집합에 속한다고 한다.
소수점 이하의 n번째 자릿수는 이러한 구성에서의 n단계의 점 위치에 반영한다. 예를 들어 점 23는 일반적인 0.2 또는 0.2000…으로 표현한다. 왜냐하면 그것은 1번째 결손 부분의 오른쪽에 위치하고 그 이후의 모든 결손 부분의 왼쪽에 위치하기 때문이다. 또한 점 13는 0.1 또는 0.0222…로 표현한다. 왜냐하면 그것은 1번째 결손 부분의 왼쪽에 위치하고 그 이후의 모든 결속 부분의 오른쪽에 위치하기 때문이다.[37]
9의 반복은 칸토어의 또 다른 일에서도 나타난다. 특히 칸토어가 1891년에 대각선 논법을 적용한 단위 구간 [0, 1]의 비가산성에 대한 적절한 증명을 부여한 것을 고려해야 한다. 이러한 증명에서는 특정한 2개의 실수가 소수 표현에 있어서 다르다는 것을 언급하는 것이 필요하다. 따라서 0.2와 0.1999…와 같은 조합은 피해야 한다. 간단한 방법은 모든 수를 무한소수로 나타내지만 이에 대한 방법은 9가 마지막에 연속되는 것을 배제한다.[내용주 7] 칸토어의 독자적인 논의에 가깝다고 할 수 있는 증명의 변형에서는 실제로 2진 표현을 사용하고 있으며 3진 표현을 2진 표현으로 바꿈으로서 칸토어 집합의 가산성을 동일하게 증명할 수 있다.[38]
전형적인 오해와 그 원인[편집]
수학을 처음 배우는 사람은 종종 0.999…와 1이 같은 것을 이해하지 못한다. 극한의 개념이나 무한소의 성질이 일상의 감각과 크게 다른 것이 그 이유로 여겨진다. 그러한 공통의 요인으로서는 다음과 같은 것이 있다.
- 학생은 "십진수로는 하나의 수는 단지 하나의 소수로 나타낼 수 있을 것이다."라고 믿는 경우가 많다. 표시가 다른 2개의 소수가 동일한 것을 알 수 있으면 그것이 역설인 것처럼 보인다. 외관상 잘 알려진 수 1의 등장으로 그러한 느낌이 더욱 강해진다.[39]
- "0.999…" 또는 이와 같은 표현은 많지만 유한 개수의 "9" 수열(아마도 가변이며 특정할 수 없는 길이)로 해석하는 학생도 있다. 비록 학생이 "9"의 무한개의 수열인 것을 받아들였다고 해도 아직 마지막 "9"가 '무한한 저쪽'에 있다고 기대하고 있을 지도 모른다.[40]
- 직관이나 애매한 가르침으로 인해 학생들은 수열의 극한을 하나의 정해진 값이 아닌 모종의 무한한 조작으로 생각하게 된다. 그것은 수열의 각 항이 그 극한에 이를 필요는 없기 때문이다. 학생이 수열과 그 극한의 차이를 받아들이더라도 그들은 "0.999…"를 극한이 아닌 수열을 의미하는 것으로 읽을 가능성이 있다.[41]
이러한 생각은 일반적인 실수를 취급하는 문맥에 있어서는 잘못되어 있다. 그러나 일반적인 경우와 다른 장면에서 적용하기 위해 발견되었거나 0.999…를 이해하는데 유익한 반례로서의 보다 정교한 수의 체계 구조에서는 이러한 생각들의 대부분이 부분적으로 옳다는 것이 나타난다.
이들 요인 가운데 상당수는 데이비드 톨(David Tall) 교수가 발견했다. 그는 자신이 맞닥뜨린 대학생들에 대한 오해 몇 가지를 학생들에게 심어주는 원인이 된 지도법과 인식의 특징을 연구했다. 수많은 학생들이 왜 처음에는 이 등식을 받아들이지 않는지 알아보기 위해 학생들을 면접하다가 다음과 같은 사실을 발견했다.[42]
학생은 0.999…를 정해진 값이 아닌 1에 한없이 가까워지는 수열로 이해합니다. 그 원인은 "선생님은 소수점 이하의 자릿수가 몇 개인지 분명히 가르쳐 주지 않았다."는 지도법의 결함 또는 "0.999…는 1보다 작은 수 중에서 존재할 수 있는 1에 가장 가까운 소수이다."라는 인식입니다.
초등적 증명 중에서 0.333… = 13의 양변을 3배로 늘리는 방법은 0.999… = 1인 것을 용인할 수 없는 학생에게 받아들이도록 만들기 위한 가장 유효한 수단인 것처럼 보인다. 그러나 제1등식을 믿는 것과 제2등식을 믿지 않는 것의 모순에 직면하면 이번에는 제1등식을 의심하기 시작하는 학생도 나타나고 또는 단지 그러한 불만을 품는 학생도 있다.[43] 이보다 간결하고 효과적인 설명 방법도 좀처럼 없다. 엄밀한 정의를 충분히 적용할 능력이 있는 학생이 0.999…를 포함해 더 나아간 수학의 결과에 놀라더라도 더 직관적인 상상에 의존할 수 있다. 예를 들어서 어떤 해석학을 배우는 학생은 0.333... = 13임을 상한한 부분 순서 집합 정의를 통해 증명할 수 있으나 그 후에도 옛 필산의 이해를 바탕으로 0.999… < 1이라고 주장했다.[44] 또 다른 학생은 13 = 0.333…인 것을 증명할 수는 있지만 분수를 통한 증명에 직면해서 '논리'가 수학 계산을 정복하고 있다고 주장한다.
조지프 메이저(Joseph Mazur)는 재능이 풍부한 또 다른 미적분학 학생을 소개한다. 그 학생은 "제가 수업에서 말한 것에는 거의 모두 이의를 제기하지만 제가 사용하고 있는 계산기에는 결코 이의를 제기하지 않습니다. 게다가 23개의 제곱근을 계산하는 것도 포함해서 수학을 하는 데에 필요한 것은 9자리(정도)로 믿게 되었습니다. 그 학생은 9.999… = 10이라는 극한의 논의에 여전히 불쾌한 느낌이었지만 그것은 "무한 추측을 하는 무한 개념의 성장 과정"(wildly imagined infinite growing process)이다."라고 불린다.[45]
에드 듀빈스키(Ed Dubinsky)에 의한 수학 학습 이론(APOS theory)의 한 부분으로서 듀빈스키와 공동 연구자(2005년)는 0.999…를 "1에서 무한히 작은 거리만 떨어져 있는 수를 나타내는 유한하고 불확정한 문자열"이라고 생각하는 학생은 "무한소수 구성 과정의 완전한 개념이 아직 형성되지 않았다."고 말했다. 예를 들어 0.999…의 구성 과정의 완전한 개념을 습득한 학생이라도 아직 그 과정을 (이미 가지고 있는 "1"의 개념과 같은) 하나의 '대상'으로서 다시 파악하지 못하고 0.999…라는 하나의 과정과 1이라는 수의 존재를 모순되는 것으로 볼 지도 모른다. 또한 듀빈스키는 "하나의 대상으로 간주한다."는 이러한 정신적 능력이 13 자체를 수로 간주하거나 자연수 집합 그 자체를 하나의 대상으로 취급한다는 점과 관련되어 있다고 본다.[46]
미디어에서의 논의[편집]
인터넷의 등장에 따라 0.999… = 1에 관한 논쟁은 교육 현장 뿐만 아니라 뉴스그룹이나 전자 게시판 등 평소에는 수학과 관련이 없던 공간에서도 화제가 되기도 한다. 뉴스그룹 sci.math에서 0.999…에 관한 논의는 '유행 스포츠'이며 FAQ에서 응답된 문제 가운데 하나이기도 하다.[47] 해당 FAQ는 13를 이용하는 방법, 10배로 높이는 방법, 극한을 이용하는 방법을 간결하게 취급하고 있고 이와 마찬가지로 코시 열도 언급하고 있다.
미국의 신문 《시카고 리더》(Chicago Reader)의 칼럼 코너인 〈더 스트레이트 도프〉(The Straight Dope) 2003년판에서는 잘못된 개념을 언급하면서 13이나 극한을 통한 0.999…에 대해 다음과 같이 논의하고 있다.
우리 안에 있는 유인원적인 요소가 "0.999…는 실제로 '수'를 나타내는 것이 아니라 '과정'을 나타내고 있습니다. 하나의 수를 찾기 위해 우리는 그러한 과정을 중간에서 끊어야 합니다. 그 시점에 있어서 0.999…=1이라는 개념은 붕괴됩니다."라고 말하면서 여전히 저항하고 있습니다. 이것은 넌센스입니다![48]
〈더 스트레이트 도프〉(The Straight Dope)는 "다른 게시판... 대부분 비디오 게임"에서 독립된 전용 게시판들을 통해 논쟁을 일으켰다. 이와 마찬가지로 0.999… 문제는 미국의 비디오 게임 개발사인 블리자드 엔터테인먼트의 배틀넷(Battle.net) 포럼에서 초반 7년 동안에 걸쳐 매우 일반적인 화제가 되기도 했다. 마이크 모하임(Mike Morhaime) 블리자드 엔터테인먼트 사장은 2004년 4월 1일에 만우절을 맞아 열린 기자 회견 도중에 0.999… = 1이라고 발표했다. 블리자드 엔터테인먼트는 나중에 공개된 보도자료에서 극한에 기반한 것과 10을 곱한 것 2가지 증명을 제공했다.
우리는 이 문제에 대한 명확한 결론을 내린 것에 매우 흥분하고 있습니다. 우리는 0.999…가 1과 같은 것인지 같지 않은 것인지에 대한 가슴앓이와 걱정거리를 지켜보고 왔습니다. 여기에 다음 증명(극한에 기반한 것과 10을 곱한 것)을 제시하여 우리 고객들에 대해 최종적으로 단호하게 이 문제에 대처하게 된 것을 기쁘게 생각합니다.[49]
관련된 문제[편집]
- 제논의 역설, 특히 아킬레우스와 거북이의 역설은 외관상 역설 0.999 = 1을 연상시킨다. 아킬레우스의 역설은 수학적으로 모델화되어 0.999와 같이 등비수열을 사용하면서 해결한다. 그렇지만 이러한 수학적인 취급이 엘레아의 제논이 탐구하고 있던 잠재적인 형이상의 문제에 대처하고 있는가의 여부에 대해서는 분명하지 않다.[50] 다만 무한합의 값(여기에서는 유한소수의 무한합으로서의 무한소수)은 부분합의 극한(변수가 일정한 법칙에 따라 정해진 값에 한없이 가까워질 때의 값)에 의해서 정의되고 있으므로 이러한 방법에서는 역설을 해결했다고 보기는 어렵다는 논의가 있다(유한합, 순환소수, 순환논법을 참조). 이러한 사실에 유의하면 0.999… = 1이라는 귀결은 극한에 의해서 무한소수의 값을 정의한 결과이며 반드시 자명한 것은 아니다(그러한 의미에서는 앞에서 언급한 "제1등식을 믿는 것과 제2등식을 믿지 않는 모순에 직면하자 제1등식을 의심하기 시작했다."[51]라는 태도가 어느 정도 수학적이고 감각적인 자세라고 볼 수도 있다). 원래 무한히 존재하는 값을 모두 더할 수 있는가라는 질문은 아직까지도 해결되지 않았으며(현대 수학에서는 정의로 처리하고 있다. 공리적 집합론 참조) 0.999… = 1이나 제논의 역설이라는 화제가 그것을 상기시켜 주는 모습의 소재임은 확실할 것이다.
- 0으로 나누기는 0.999…에 대한 일반적인 몇 가지 논의에서 볼 수 있지만 그것 또한 논쟁의 대상이 되기도 한다. 많은 저자들이 0.999…를 정의하는 것을 선택하는 한편 실수의 현대적 취급에서는 0에 의한 나눗셈은 정의되지 않는다라고 언급하는 것은 그것이 일반적인 실수의 범위에서는 의미를 부여할 수 없기 때문이다. 그렇지만 0에 의한 나눗셈은 복소해석학을 비롯한 다른 체계에서는 정의되어 있다. 복소해석학에서는 확장된 복소평면(리만 구)은 무한원점을 갖는다. 10을 무한대로 정의했다는 사실은 의미가 있다.[52] 또한 실제로 그 결과는 심오한 편인데 공학이나 물리학에도 응용할 수 있다. 유명한 몇몇 수학자들은 수 체계가 훨씬 발달하기 이전부터 그러한 정의를 논의했다.[53]
- 장황한 수 표기와 비슷한 사례로서 −0을 들 수 있다. 실수 등의 수 체계에서 "0"은 덧셈에 관한 항등원을 의미하며 양수도 음수도 아니다. 일반적으로 "-0"은 덧셈에 관한 0의 역원을 나타낸다고 해석되므로 −0 = 0이어야 한다.[54] 이는 몇몇 컴퓨터의 수체계(예를 들면 부호화된 숫자 표현, 1의 보수 표현, IEEE 754에서의 정의와 같은 부동소수점 표시)에서도 그러하다.[55] IEEE(전기 전자 기술자 협회) 부동소수점의 경우 -0은 주어진 정확한 수치를 나타내기에는 (절댓값이) 너무 작지만 그래도 여전히 음수인 값을 나타낸다. 따라서 IEEE 부동소수점 표시에서 "-0"은 원래 의미에서 "-0"이 아니다.
같이 보기[편집]
각주[편집]
내용주[편집]
- ↑ 가 나 cf. 같은 주제에 따른 이진법 버전도 해당 문헌에 존재한다. Silvanus P. Thompson, Calculus made easy, St. Martin's Press, New York, 1998. ISBN 0-312-18548-0.
- ↑ 통합의 역사적인 과정은 다음을 참조하라: Griffiths and Hilton (p.xiv) in 1970. 또다른 문헌은 다음을 참고하라: Pugh (p.10) in 2001. 둘 다 실제로는 공리적 해석론보다는 데데킨트 절단을 선호한다. 절단 방법에 대한 교과서는 다음을 참조하라: Pugh p.17 or Rudin p.17. 논리적 시점에 대해서는 다음을 참조하라: Pugh p.10, Rudin p.ix, or Munkres p.30.
- ↑ 엔더턴(Enderton, p.113)는 다음과 같은 글을 남겼다. "데데킨트 절단 배경에 있는 아이디어는 유리수, 즉 x보다 더 작은 모든 유리수의 무한 집합을 부여받음으로써 실수 x가 명명된다는 것이다. 순환논법을 피하기 위해 이러한 방법으로 얻을 수 있는 유리수의 집합이 특징되어야 한다."
- ↑ 비표준적인 수의 완전한 취급은 로빈슨의 《비표준적인 분석》(Non-standard Analysis) 참조.
- ↑ 벌캠프(Berlekamp), 콘웨이(Conway), 가이(Guy, pp.79-80, 307-311)는 1과 13에 대해 논의하고 있으며 나아가 1ω에 대해 언급하고 있다. 0.111…의 게임은 벌캠프의 규칙을 직접 따르고 있으며 이는 다음 문헌에 기술되어 있다. A. N. Walker (1999년). “Hackenstrings and the 0.999⋯ =1 FAQ”. 2006년 6월 16일에 원본 문서에서 보존된 문서. 2006년 6월 29일에 확인함.
- ↑ Richman pp.398-400. 러딘(Rudin, p.23)은 제1장의 마지막 연습 문제로서 이러한 대체 구조(다만 실수에 한함)를 선택하고 있다.
- ↑ 마오르(Maor, p.60)와 만키에비치(Mankiewicz, p.151)는 전자의 방법을 되돌아본다. 만키에비치는 그것이 칸토어의 일이라고 정의했는데 첫 출처는 확실하지 않다. 멍크리스(Munkres, p.50)는 후자의 방법을 언급하고 있다.
참고주[편집]
- ↑ Rudin p.61, Theorem 3.26; J. Stewart p.706
- ↑ Euler p.170
- ↑ Grattan-Guinness p.69; Bonnycastle p.177
- ↑ 이러한 예는 다음과 같은 문헌에 나타난다: J. Stewart p.706, Rudin p.61, Protter and Morrey p.213, Pugh p.180, J.B. Conway p.31.
- ↑ 이 극한의 예에 대해서는 다음과 같은 문헌에 따른다: Rudin p.57, Theorem 3.20e. 보다 직접적인 접근에 대해서는 다음 문헌을 참조하라: Finney, Weir, Giordano (2001) Thomas' Calculus: Early Transcendentals 10ed, Addison-Wesley, New York. Section 8.1, example 2(a), example 6(b).
- ↑ Davies p.175; Smith and Harrington p.115
- ↑ Beals p.22; I. Stewart p.34
- ↑ Bartle and Sherbert pp.60-62; Pedrick p.29; Sohrab p.46
- ↑ Apostol pp.9, 11-12; Beals p.22; Rosenlicht p.27
- ↑ Apostol p.12
- ↑ Rudin pp.17-20, Richman p.399, or Enderton p.119. 정확하게는 이들 세 사람은 이러한 절단을 각각 1*, 1−, 1R이라고 부르고 있다. 세 사람 모두 전통적인 1의 정의와 동일시하고 있는데 러딘(Rudin)과 엔더턴(Enderton)이 "데데킨트 절단"이라고 부르는 것에 비해 리치먼(Richman)이 "중요하지 않은 데데킨트 절단"이라고 부르는 것에 주의해야 한다.
- ↑ Richman p.399
- ↑ 가 나 J J O'Connor; E F Robertson (2005년 10월). “History topic: The real numbers: Stevin to Hilbert”. MacTutor History of Mathematics. 2007년 9월 29일에 원본 문서에서 보존된 문서. 2006년 8월 30일에 확인함.
- ↑ “Mathematics Magazine:Guidelines for Authors”. The Mathematical Association of America. 2006년 8월 23일에 확인함.
- ↑ Richman pp.398-399
- ↑ Griffiths & Hilton §24.2 "Sequences" p.386
- ↑ Griffiths & Hilton pp.388, 393
- ↑ Griffiths & Hilton p.395
- ↑ Griffiths & Hilton pp. vii, 395
- ↑ Gowers p.60
- ↑ Lightstone pp.245-247
- ↑ Katz & Katz 2010
- ↑ Stewart 2009, p.175; the full discussion of 0.999… is spread through pp.172-175.
- ↑ José Amado, Benardete (1964). 《Infinity: An essay in metaphysics》. Clarendon Press. 279쪽. 2011년 11월 27일에 확인함.
- ↑ Richman pp.397-399
- ↑ Gardiner p.98; Gowers p.60
- ↑ 가 나 Fjelstad p.11
- ↑ Fjelstad pp.14-15
- ↑ DeSua pp.902-903
- ↑ Petkovšek p.408
- ↑ Protter and Morrey p.503; Bartle and Sherbert p.61
- ↑ Komornik and Loreti p.636
- ↑ Kempner p.611; Petkovšek p.409
- ↑ Petkovšek pp.410-411
- ↑ Leavitt 1984 p.301
- ↑ Lewittes pp.1-3; Leavitt 1967 pp.669, 673; Shrader-Frechette pp.96-98
- ↑ Pugh p.97; Alligood, Sauer, and Yorke pp.150-152. 프로터(Protter)와 모리(Morrey, p.507), 페드릭(Pedrick, p.29)은 이 이 기술을 연습 문제로서 평가하고 있다.
- ↑ Rudin p.50, Pugh p.98
- ↑ Bunch, p.119; Tall and Schwarzenberger, p.6. 마지막 제안은 Burrell(p.28)에 따른다. 즉 "아마도 모든 수 중에서 가장 안심되는 수는 1일 것이다. 따라서 0.999…를 1로 취급할 때에 유난히 불안감을 느낀다."
- ↑ Tall and Schwarzenberger pp.6-7; Tall 2000 p.221
- ↑ Tall and Schwarzenberger p.6; Tall 2000 p.221
- ↑ Tall 2000 p.221
- ↑ Tall 1976 pp.10-14
- ↑ Pinto and Tall p.5, Edwards and Ward pp.416-417
- ↑ Mazur pp.137-141
- ↑ Dubinsky 외 261-262
- ↑ 리치먼(Richman, p.396)이 해당 사실을 언급했다.Hans de Vreught (1994년). “sci.math FAQ: Why is 0.9999… = 1?”. 2006년 6월 29일에 확인함.
- ↑ Cecil Adams (2003년 7월 11일). “An infinite question: Why doesn't .999~ = 1?”. 《The Straight Dope》. The Chicago Reader. 2006년 9월 6일에 확인함.
- ↑ “Blizzard Entertainment® Announces .999~ (Repeating) = 1”. 《Press Release》. Blizzard Entertainment. 2004년 4월 1일. 2007년 1월 20일에 원본 문서에서 보존된 문서. 2006년 9월 3일에 확인함.
- ↑ Wallace p.51, Maor p.17
- ↑ Tall 1976 pp.10-14
- ↑ 이러한 예는 다음을 참고하라. J.B. Conway's treatment of Möbius transformations, pp.47-57
- ↑ Maor p.54
- ↑ Kroemer, Herbert; Kittel, Charles (1980년). 《Thermal Physics》 2e판. W. H. Freeman. 462쪽. ISBN 0-7167-1088-9.
- ↑ “Floating point types”. MSDN C# Language Specification (마이크로소프트 개발자 네트워크 C 언어 사양). 2006년 8월 29일에 확인함.
참고 문헌[편집]
- Alligood; Sauer; Yorke (1996년). 〈4.1 Cantor Sets〉. 《Chaos: An introduction to dynamical systems》. Springer. ISBN 0-387-94677-2.
- 역학계에 관한 이 입문적인 교과서는 학부생 또는 초급 대학원생 대상이다(p.ix).
- Apostol, Tom M. (1974년). 《Mathematical analysis》 2e판. Addison-Wesley. ISBN 0-201-00288-4.
- 미적분학에서 보다 발전된 해석학 "수학 분석"(Mathematical analysis)으로의 변천이 "속이지 않고, 엄밀하고, 최신임과 동시에 학자 티를 내는 일이 없도록" 의도하고 있다(서문). 어포스톨(Apostol)은 실수의 구성에 상한의 존재 공리를 응용하고 있는데 무한소수는 2쪽 이후에 소개하고 있다(pp.9-11).
- Bartle, R.G.; D.R. Sherbert (1982년). 《Introduction to real analysis》. Wiley. ISBN 0-471-05944-7.
- 이 교과서는 "실제 해석의 기본적 성질과 기교를 다루는 이해하기 쉽고 적당한 진도의 교과서"를 지향한다. 실수의 구성에는 상한의 존재 공리를 이용하고 있다(pp. vii-vii).
- Beals, Richard (2004년). 《Analysis》. Cambridge UP. ISBN 0-521-60047-2.
- Berlekamp, E.R.; J.H. Conway; R.K. Guy (1982년). 《Winning Ways for your Mathematical Plays》. Academic Press. ISBN 0-12-091101-9.
- Berz, Martin (1992년). “Automatic differentiation as nonarchimedean analysis”. 《Computer Arithmetic and Enclosure Methods》 (Elsevier): 439-450.
- Bunch, Bryan H. (1982년). 《Mathematical fallacies and paradoxes》. Van Nostrand Reinhold. ISBN 0-442-24905-5.
- 이 책은 중심적인 화제인 "수학적 현실성과 물리적 현실성의 다소 희박한 관계"를 살펴보는 도구로서 역설과 잘못된 추론에 의한 해석을 소개한다. 고등학교 1학년 정도의 대수를 가정하고 있으며 (제2장의 등비수열을 포함해서) 더욱 진전된 수학은 이 책에서 발전해 간다. 0.999…는 완전히 다루어지는 것들 가운데 하나는 아니지만 칸토어의 대각선 논법을 다루는 가운데 간결하게 서술되어 있다(pp.ix-xi, 119).
- Burrell, Brian (1998년). 《Merriam-Webster's Guide to Everyday Math: A Home and Business Reference》. Merriam-Webster. ISBN 0-87779-621-1.
- Conway, John B. (1978년) [1973년 초판]. 《Functions of one complex variable I》 2e판. Springer-Verlag. ISBN 0-387-90328-3.
- 이 교과서는 필수 과목으로서의 "기본적인 미적분의 엄밀한 과정"의 역할을 담당하고 있으며 기술되어 있는 그 원칙은 "수학 입문"(An Introduction to Mathematics)으로서 복소해석학을 소개하고 대상을 명확하고 정확하게 밝히는 것이다(p. vii).
- Davies, Charles (1846년). 《The University Arithmetic: Embracing the Science of Numbers, and Their Numerous Applications》. A.S. Barnes.
- DeSua, Frank C. (1960년 11월). “A system isomorphic to the reals” (접근이 제한되어 있음). 《The American Mathematical Monthly》 67 (9): 900-903.
- Dubinsky, Ed; Kirk Weller; Michael McDonald; Anne Brown (2005년). “Some historical issues and paradoxes regarding the concept of infinity: an APOS analysis: part 2”. 《Educational Studies in Mathematics》 60: 253-266. doi:10.1007/s10649-005-0473-0.
- Edwards, Barbara; Michael Ward (2004년 5월). “Surprises from mathematics education research: Student (mis)use of mathematical definitions”. 《The American Mathematical Monthly》 111 (5): 411-425.
- Enderton, Herbert B. (1977년). 《Elements of set theory》. Elsevier. ISBN 0-12-238440-7.
- 집합론에 입문하는 학부 학생용 교과서로 "특별한 예비 지식을 전제로 하지 않는 것"이 특징이다. 공리적 집합론 또는 수 체계의 구성에 초점을 둔 학습 과정을 제공하기 위해 쓰여져 있지만 공리라는 소재는 별로 중요시되지 않는 방식으로 다루어지고 있다(pp.xi-xii).
- Euler, Leonhard (1822년) [1770년 초판]. John Hewlett and Francis Horner, English translators., 편집. 《Elements of Algebra》 (영어) 제3판. Orme Longman.
- Fjelstad, Paul (1995년 1월). “The repeating integer paradox” (접근이 제한되어 있음). 《The College Mathematics Journal》 26 (1): 11-15. doi:10.2307/2687285.
- Gardiner, Anthony (2003년) [1982년 초판]. 《Understanding Infinity: The Mathematics of Infinite Processes》. Dover. ISBN 0-486-42538-X.
- Gowers, Timothy (2002년). 《Mathematics: A Very Short Introduction》. Oxford UP. ISBN 0-19-285361-9.
- Grattan-Guinness, Ivor (1970년). 《The development of the foundations of mathematical analysis from Euler to Riemann》. MIT Press. ISBN 0-262-07034-0.
- Griffiths, H.B.; P.J. Hilton (1970년). 《A Comprehensive Textbook of Classical Mathematics: A Contemporary Interpretation》. London: Van Nostrand Reinhold. ISBN 0-442-02863-6. (LCC QA37.2 G75)
- Kempner, A.J. (1936년 12월). “Anormal Systems of Numeration” (접근이 제한되어 있음). 《The American Mathematical Monthly》 43 (10): 610-617.
- Komornik, Vilmos; Paola Loreti (1998년). “Unique Developments in Non-Integer Bases” (접근이 제한되어 있음). 《The American Mathematical Monthly》 105 (7): 636-639.
- Leavitt, W.G. (1967년). “A Theorem on Repeating Decimals” (접근이 제한되어 있음). 《The American Mathematical Monthly》 74 (6): 669-673.
- Leavitt, W.G. (1984년 9월). “Repeating Decimals” (접근이 제한되어 있음). 《The College Mathematics Journal》 15 (4): 299-308.
- Lewittes, Joseph (2006년). “Midy's Theorem for Periodic Decimals”. 《New York Number Theory Workshop on Combinatorial and Additive Number Theory》. arXiv. 2008년 3월 6일에 확인함.
- Lightstone, A.H. (1972년 3월). “Infinitesimals” (접근이 제한되어 있음). 《The American Mathematical Monthly》 79 (3): 242-251.
- Mankiewicz, Richard (2000년). 《The story of mathematics》. Cassell. ISBN 0-304-35473-2.
- 만키에비치(Mankiewicz)는 수학, 수학자의 저작, 역사적 개략의 시각적인 측면과 질적인 측면을 조합함으로써 수학의 역사를 "이해하기 쉬운 형식"으로 서술하고자 한다(p.8).
- Maor, Eli (1987년). 《To infinity and beyond: a cultural history of the infinite》. Birkhäuser. ISBN 3-7643-3325-1.
- 연대순이라기보다 화제별 무한에 관한 회고. 이 책은 "일반적인 독자를 의도하고 있다"가 "수학자의 시점에서 말하고 있다". 수학적인 엄밀성과 읽기 쉬운 말투 사이에서 마오르(Maor)는 "이 문제를 올바르게 다루는 데 성공하기를 바란다."고 말하고 있다(pp.x-xiii).
- Mazur, Joseph (2005년). 《Euclid in the Rainforest: Discovering Universal Truths in Logic and Math》. Pearson: Pi Press. ISBN 0-13-147994-6.
- Munkres, James R. (2000년) [1975년 초판]. 《Topology》 2e판. Prentice-Hall. ISBN 0-13-181629-2.
- 형식적인 예비 지식을 필요로 하지 않고 "대학 3 ~ 4학년 또는 대학원 1학년 수준"에서의 입문서를 의도하고 있으며 "독자가 집합론에 대해 잘 알고 있음을 가정조차 하지 않는 편"이다(p.xi). 멍크리스(Munkres)의 실제 수 취급은 공리적이며 이러한 도구를 갖지 않는다. 그는 이러한 구성 방법에 대해 "이러한 접근법은 많은 시간과 노력을 필요로 하며 수학적인 흥미로 다루는 것보다 훨씬 논리적이다."라고 말하고 있다(p.30).
- Pedrick, George (1994년). 《A First Course in Analysis》. Springer. ISBN 0-387-94108-8.
- Petkovšek, Marko (1990년 5월). “Ambiguous Numbers are Dense” (접근이 제한되어 있음). 《American Mathematical Monthly》 97 (5): 408-411.
- Pinto, Márcia; David Tall (2001년). “Following students' development in a traditional university analysis course” (PDF). 《PME25》: v4: 57-64.
- Protter, M.H.; C.B. Morrey (1991년). 《A first course in real analysis》 2e판. Springer. ISBN 0-387-97437-7.
- 이 책은 "미적분학의 표준적 가정을 마친 학생에게 적절한, 해석학의 이론적 구성을 소개하는 것"을 목표로 한다(p. vii). 제2장의 끝에서 저자는 실수에 대해 유계 단조열이 수렴한다고 하는 것을 공리로서 가정하고 있지만, 그 후에 구간 축소법과 상한의 존재를 증명하고 있다(pp.56-64). 소수 전개는 부록 3 "모든 기초에서의 실수의 확장"(Appendix 3 "Expansions of real numbers in any base"에서 볼 수 있다(pp.503-507).
- Pugh, Charles Chapman (2001년). 《Real mathematical analysis》. Springer-Verlag. ISBN 0-387-95297-7.
- 실수가 잘 알려진 성질을 가정하는 한편 퓨(Pugh)는 가능한 한 빠른 단계에서 실수의 절단을 소개한다.공리적인 취급에 대해 "실수의 체계에 근거해 실수가 구성되어 있는 것을 생각하면 이것은 하나의 사기이다."라고 말하고 있다(p.10). 상한의 존재의 성질과 그것과 관계하는 몇 가지 사실을 증명한 후에는 그 외의 장면에서 절단은 이용되지 않는다.
- Richman, Fred (1999년 12월). “Is 0.999… = 1?” (접근이 제한되어 있음). 《Mathematics Magazine》 72 (5): 396-400. 무료 HTML 출판 전 논문: Richman, Fred (1999년 6월 8일). “Is 0.999… = 1?”. 2006년 2월 3일에 원본 문서에서 보존된 문서. 2006년 8월 23일에 확인함. 주의: 잡지의 논문에는 출판 전 논문에는 볼 수 없는 기술이 포함되어 있다.
- Robinson, Abraham (1996년). 《Non-standard analysis》 Revis판. Princeton University Press. ISBN 0-691-04490-2.
- Rosenlicht, Maxwell (1985년). 《Introduction to Analysis》. Dover. ISBN 0-486-65038-3.
- Rudin, Walter (1976년) [1953년 초판]. 《Principles of mathematical analysis》 3e판. McGraw-Hill. ISBN 0-07-054235-X.
- 보다 진행된 학부생의 과정을 위한 교과서. 유리수로 실수를 구성하는 방법부터 시작하는 것은 (논리적으로는 옳지만) 교육상 바람직하지 않다는 것을 경험상 확신한다. 초기 단계에서는 많은 학생들이 이 일의 필요성에 대해 그 가치를 인정하지 못한다. 그 때문에, 실수의 체계는 상한이 존재하는 실수체로서 소개되어 이 성질의 흥미로운 몇 가지의 응용 사례가 곧바로 이루어진다. 데데킨트의 구성은 무시되고 있다. 이제 이것은 제1장 부록(Appendix)에 있으며 때가 되면 언제든지 공부하고 즐길 수 있다(p.ix).
- Shrader-Frechette, Maurice (1978년 3월). “Complementary Rational Numbers” (접근이 제한되어 있음). 《Mathematics Magazine》 51 (2): 90-98.
- Smith, Charles; Charles Harrington (1895년). 《Arithmetic for Schools》. Macmillan.
- Sohrab, Houshang (2003년). 《Basic Real Analysis》. Birkhäuser. ISBN 0-8176-4211-0.
- Stewart, Ian (1977년). 《The Foundations of Mathematics》. Oxford UP. ISBN 0-19-853165-6.
- Stewart, James (1999년). 《Calculus: Early transcendentals》 4e판. Brooks/Cole. ISBN 0-534-36298-2.
- 이 책은 "학생들이 미적분을 이해하는 것을 지원하고 관념에 대한 이해를 키우는 것"을 목적으로 한다(p.v). 미적분의 기본 성질의 증명은 생략되어 있다.
- D.O. Tall; R.L.E. Schwarzenberger (1978년). “Conflicts in the Learning of Real Numbers and Limits” (PDF). 《Mathematics Teaching》 82: 44-49.
- Tall, David (1976년 7월). “Conflicts and Catastrophes in the Learning of Mathematics” (PDF). 《Mathematical Education for Teaching》 2 (4): 2-18.
- Tall, David (2000년). “Cognitive Development In Advanced Mathematics Using Technology” (PDF). 《Mathematics Education Research Journal》 12 (3): 210-230.
- von Mangoldt, Dr. Hans (1911년). 〈Reihenzahlen〉. 《Einführung in die höhere Mathematik》 (독일어) 제1판. Leipzig: Verlag von S. Hirzel.
- Wallace, David Foster (2003년). 《Everything and more: a compact history of infinity》. Norton. ISBN 0-393-00338-8.
외부 링크[편집]
 위키미디어 공용에 0.999… 관련 미디어 분류가 있습니다.
위키미디어 공용에 0.999… 관련 미디어 분류가 있습니다.- .999999... = 1? from cut-the-knot
- Ask A Scientist: Repeating Decimals
- Proof of the equality based on arithmetic
- Repeating Nines
- Point nine recurring equals one
- David Tall's research on mathematics cognition
- What is so wrong with thinking of real numbers as infinite decimals?
- Theorem 0.999... on Metamath
- Hackenstrings, and the 0.999... ?= 1 FAQ
- 네이버캐스트 0.999...는 1인가?























![{\displaystyle [1,n]\subseteq \{n\in {}^{\ast }\mathbb {Z} _{+}\mid d(n)=3\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/944cb9758a042b0c8338050e293f7d1efc01795e)



