황금비

황금비는 어떠한 선으로 이등분하여 한쪽의 평방을 다른쪽 전체의 면적과 같도록 하는 분할이다. 즉, 선 AB위에 점 C가 있을 때 (AC)^2＝BC×AB 또는 AC：CB＝AB：AC가 되도록 분할하는 것이다. 이 비의 값은 로, 1.61803398....：1 또는 1：0.61803398...이 되는데 이것을 황금비라 한다. 황금비는 고대 그리스인에 의하여 발견되었고, 이후 유럽에서 가장 조화롭고 아름다운 비례(프로포션)로 간주되었다(a+b):a = a:b

황금비(黃金比, 영어: golden ratio) 또는 황금 분할(黃金分割)은 어떤 두 수의 비율이 그 합과 두 수중 큰 수의 비율과 같도록 하는 비율을 뜻한다. 즉, $(a+b)/a=a/b$인 유일한 양의 비율 $a/b$이다. 이 방정식을 $x=a/b$를 사용하여 다시 적으면 이차 방정식 $x^{2}-x-1=0$이 된다. 이 이차 방정식은 양의 실수

$\phi ={\frac {1+{\sqrt {5}}}{2}}=1.618\cdots$

와 음의 실수

$1-\phi =-{\frac {1}{\phi }}={\frac {1-{\sqrt {5}}}{2}}=-0.618\cdots$

를 두 근으로 한다. 이 가운데 양의 실근 $\phi$을 황금비로 삼는다. 황금비는 무리수이자 대수적 수이며, 약 1.618을 근삿값으로 한다. 기호는 그리스 문자 피(φ, TeX $\phi$ 또는 $\varphi$)를 쓴다.

유클리드(원론 3, 141)가 그 특징을 연구한 이래로 많은 수학자들이 자연에서 찾을 수 있는 황금비율을 연구해 왔다.

정의

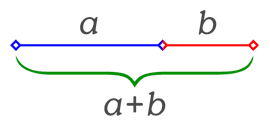
황금비는 어떠한 선으로 이등분하여 한쪽의 평방을 다른쪽 전체의 면적과 같도록 하는 분할이다. 즉, 선 AB위에 점 C가 있을 때 (AC)^2＝BC×AB 또는 AC：CB＝AB：AC가 되도록 분할하는 것이다. 이 비의 값은 ${\frac {{\sqrt {5}}+1}{2}}$로, 1.61803398....：1 또는 1：0.61803398...이 되는데 이것을 황금비라 한다.

(이 황금비는 이차방정식 $x^{2}-x-1$의 해와 같다)

황금비는 고대 그리스인에 의하여 발견되었고, 이후 유럽에서 가장 조화롭고 아름다운 비례(프로포션)로 간주되었다. 근대에 이르러 르 코르뷔지에는 황금비를 피보나치(Fibonacci) 수열의 원리에서 착안하여 인체비례와 결부시켜 '모듈(황금기준척)'을 고안했다. '섹숑 도르'(프랑스어: Section d'Or, 황금비율)라는 이름을 붙인 입체파의 화가그룹도 있다.

황금비 $\color {Blue}\varphi$(phi)는 선분을 $a,b$ 길이로 둘로 나눌 때, 다음과 같은 값으로 정의된다.

${\frac {a+b}{a}}={\frac {a}{b}}=\varphi$

이 때,

$\left({\frac {a}{b}}\right)^{2}={\frac {a}{b}}+1\qquad \qquad (*)$

가 성립하고,

황금비를 소수점 이하 50자리까지 나타내면 다음과 같다 (OEIS의 수열 A001622).

1.61803 39887 49894 84820 45868 34365 63811 77203 09179 80576

수학적 성질

황금비는 기하학에서 자주 등장하는 수학 상수이다. 특히 오각형에 연관성이 크다. 예를 들어, 정오각형의 한 변의 길이와 대각선의 길이의 비는 황금비이다.

정십이면체에서 나오는 황금비율의 표현

정이십면체에서 표현되는 황금비의 표현

또한 오각형에서 황금비가 발견되는 만큼 오각형과 관련이 있는 도형은 황금비와도 관련이 있는 경우가 많다. 예를 들어, 각 면이 정오각형으로 이루어진 정십이면체와 정십이면체의 각 면의 무게중심을 꼭짓점으로 하는 정이십면체는, 모든 꼭짓점을 한 면에 평행한 평면에 정사영시켰을 때 나오는 도형에서 바깥쪽의 꼭짓점들을 지나는 원과 안쪽의 꼭짓점들을 지나는 원의 반지름의 비가 황금비이다. 입체도형의 정사영이 가지는 성질에 비추어 볼 때, 이는 정십이면체와 정이십면체를 눈으로 볼 때 황금비가 관찰되는 것으로 해석할 수 있다.

피보나치 수는 황금비를 포함한다.

$F\left(n\right)={{\varphi ^{n}-(1-\varphi )^{n}} \over {\sqrt {5}}}={{\varphi ^{n}-(-\varphi )^{-n}} \over {\sqrt {5}}}$

또한, 피보나치 수열의 두 수의 비의 극한값은 황금비이다.

황금비의 다른 표현

• 연분수로 표현한 황금비

$\varphi =1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\ddots }}}}}}=[1;1,1,1,\dots ]$

• 다중근호로 표현한 황금비

${\sqrt {1+{\sqrt {1+{\sqrt {1+{\sqrt {1+{\sqrt {1...}}}}}}}}}}=\varphi$

같이 보기

• 미학
• 황금각
• Φ
• 황금함수
• 황금사각형
• 황금삼각형
• 플라스틱 수
• 피보나치 수열
• 닮음 (기하학)
• 백은비

참고 문헌

이 문서에는 다음커뮤니케이션(현 카카오)에서 GFDL 또는 CC-SA 라이선스로 배포한 글로벌 세계대백과사전의 〈황금분할〉 항목을 기초로 작성된 글이 포함되어 있습니다.

외부 링크

• 위키미디어 공용에 황금비 관련 미디어 자료가 있습니다.
• "Golden Section" by Michael Schreiber, Wolfram Demonstrations Project, 2007.
• Hrant Arakelian. Mathematics and History of the Golden Section, Logos 2014, 404 p. ISBN 978-5-98704-663-0 (rus.).