피보나치 수

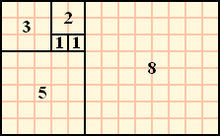
피보나치 수를 이용한 사각형 채우기

수학에서 피보나치 수(영어: Fibonacci numbers)는 첫째 및 둘째 항이 1이며 그 뒤의 모든 항은 바로 앞 두 항의 합인 수열이다. 처음 여섯 항은 각각 1, 1, 2, 3, 5, 8이다. 편의상 0번째 항을 0으로 두기도 한다.

역사

피보나치 수가 처음 언급된 문헌은 기원전 5세기 인도의 수학자 핑갈라가 쓴 책이다.

유럽에서 피보나치 수를 처음 연구한 것은 레오나르도 피보나치로 토끼 수의 증가에 대해서 이야기하면서 이 수에 대해 언급했다. n 번째 달의 토끼 수는

• 첫 달에는 새로 태어난 토끼 한 쌍만이 존재한다.
• 두 달 이상이 된 토끼는 번식 가능하다.
• 번식 가능한 토끼 한 쌍은 매달 새끼 한 쌍을 낳는다.
• 토끼는 죽지 않는다.

따라서 첫 달에는 새로 태어난 토끼 한 쌍이 있고, 두 번째 달에는 그대로 토끼 한 쌍, 세 번째 달부터는 이 토끼 한 쌍이 새끼를 낳게 되어 토끼가 2쌍이 되고, 네 번째 달에는 3쌍, 다섯 번째 달에는 5쌍이 된다. 이때 n번째 달에 a 쌍의 토끼가 있었고, 다음 n+1번째 달에는 새로 태어난 토끼를 포함해 b쌍이 있었다고 하자. 그러면 그다음 n+2 번째 달에는 a+b 쌍의 토끼가 있게 된다. 이는 n번째 달에 살아있던 토끼는 충분한 나이가 되어 새끼를 낳을 수 있지만, 바로 전 달인 n+1번째 달에 막 태어난 토끼는 아직 새끼를 낳을 수 없기 때문이다.

정의

점화식을 통한 정의

피보나치 수 $F_{n}$는 다음과 같은 초기값 및 점화식으로 정의되는 수열이다.

$F_{1}=F_{2}=1$

$F_{n}=F_{n-1}+F_{n-2}\qquad (n\in \{3,4,\dots \})$

0번째 항부터 시작할 경우 다음과 같이 정의된다.

$F_{0}=0$

$F_{1}=1$

$F_{n}=F_{n-1}+F_{n-2}\qquad (n\in \{2,3,4,\dots \})$

처음 몇 피보나치 수(0번째부터 시작할 경우)는 다음과 같다.

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, … (OEIS의 수열 A000045)

일반항

피보나치 수의 일반항은 다음과 같다.

$F_{n}={\frac {(1+{\sqrt {5}})^{n}-(1-{\sqrt {5}})^{n}}{2^{n}{\sqrt {5}}}}={\frac {1}{\sqrt {5}}}\left(\left({\frac {1+{\sqrt {5}}}{2}}\right)^{n}-\left({\frac {1-{\sqrt {5}}}{2}}\right)^{n}\right)={\frac {\varphi ^{n}-(1-\varphi )^{n}}{\sqrt {5}}}$

여기서 $\varphi =(1+{\sqrt {5}})/2$는 황금비이며, ${\sqrt {5}}$는 5의 음이 아닌 제곱근이다. 이를 비네 공식(영어: Binet's formula)이라고 한다. 이는 레온하르트 오일러가 1765년 처음 발표했으나 잊혔다가, 1848년 자크 비네에 의해 재발견되었다.

증명

피보나치 수열의 일반항에 대한 증명은 아래와 같다.

a+b=1, ab=-1 인 두 실수 a,b를 가정하자. 그러면 a,b는 이차방정식 $x^{2}-x-1=0$ 의 두 근이고 이때 판별식 D>0이므로 실수 a,b는 존재함을 알 수 있다.

그러면 피보나치 수열의 점화식 $F_{n+2}=F_{n+1}+F_{n}$ 을 $F_{n+2}=(a+b)F_{n+1}-abF_{n}$ 으로 쓸 수 있고,

우변의 $aF_{n+1}$ 을 좌변으로 이항하면 $F_{n+2}-aF_{n+1}=b(F_{n+1}-aF_{n})$ 이 된다. 즉 양변에 동일한 형태를 만들어주었으므로, 이제 $(F_{n+1}-aF_{n})$ 을 등비수열로 다룰 수 있게 된다. 이때 초항은 $F_{2}-aF_{1}$ 이고, 공비는 b가 된다.

따라서 등비수열의 일반항 공식을 이용해주면 $F_{n+1}-aF_{n}=b^{n-1}(F_{2}-aF_{1})$ 이 된다. 그런데 피보나치 수열에서 첫항과 둘째항은 둘 다 1이므로, 다시 써주면 $F_{n+1}-aF_{n}=b^{n}$ ($\cdots$ 식 1)이다(a+b=1에 의해 1-a=b이므로).

그런데 위의 변형된 피보나치 점화식에서 a와 b는 대칭적인 위치에 있으므로, $F_{n+2}=(a+b)F_{n+1}-abF_{n}$ 에서 우변의 $bF_{n+1}$ 을 좌변으로 이항한 뒤 같은 방식으로 변형해주면 $F_{n+1}-bF_{n}=a^{n}$ ($\cdots$ 식 2)으로 써줄 수 있다.

이제 식1과 식2를 변변끼리 빼주면, $(b-a)F_{n}=b^{n}-a^{n}$ , $$\therefore F_{n}=(b^{n}-a^{n})/(b-a)$$이다. 이때 앞선 이차방정식 $x^{2}-x-1=0$ 을 통해 a와 b를 직접 구해주면 둘 중 하나가 황금비가 나오는데, a와 b 중 어떤 것을 황금비로 설정하든 결과는 같다. a와 b는 대칭적인 위치에 있기 때문이다. b를 황금비라고 치면, $b=\varphi$ , $a=1-\varphi$ 이므로 $F_{n}={\frac {\varphi ^{n}-(1-\varphi )^{n}}{\sqrt {5}}}$ 이 된다.

성질

항등식

다음과 같은 항등식이 성립하며, 카시니 항등식(영어: Cassini's identity)이라고 한다.

$F_{n+1}F_{n-1}-{F_{n}}^{2}=(-1)^{n}$

다음과 같은 항등식이 성립하며, 이를 도가뉴 항등식(영어: d'Ocagne's identity)이라고 한다.

$F_{m+n}=F_{m-1}F_{n}+F_{m}F_{n+1}$

다음과 같은 항등식이 성립한다.

$\varphi ^{n}=F_{n}\varphi +F_{n-1}$

피보나치 수를 점화식을 통해 음의 정수에까지 확장할 수 있다. 이 경우, 비네 공식이 여전히 성립하며, 또한 다음이 성립한다.

$F_{-n}=(-1)^{n+1}F_{n}$

급수 공식

처음 몇 피보나치 수의 합, 교대합, 제곱합, 세제곱합은 다음과 같다.

$\sum _{k=0}^{n}F_{k}=F_{n+2}-1$

$\sum _{k=0}^{n}(-1)^{k+1}F_{k}=(-1)^{n+1}F_{n-1}+1$

$\sum _{k=0}^{n}F_{k}^{2}=F_{n}F_{n+1}$

$\sum _{k=0}^{n}F_{k}^{3}={\frac {F_{3n+2}+(-1)^{n+1}6F_{n-1}+5}{10}}$

처음 몇 피보나치 수의 홀수째, 짝수째, 3의 배수째 항의 합은 다음과 같다.

$\sum _{k=1}^{n}F_{2k-1}=F_{2n}$

$\sum _{k=0}^{n}F_{2k}=F_{2n+1}-1$

$\sum _{k=0}^{n}F_{3k}={\frac {F_{3n+2}-1}{2}}$

피보나치 수의 역수의 합은 수렴하며, 또한 다음 항등식들이 성립한다.

${\begin{aligned}\sum _{n=1}^{\infty }{\frac {1}{F_{n}}}&=3+\sum _{n=1}^{\infty }{\frac {(-1)^{n}}{F_{n}F_{n+1}F_{n+2}}}\\&={\frac {41}{12}}-{\frac {3}{2}}\sum _{n=1}^{\infty }{\frac {1}{F_{n}F_{n+1}F_{n+2}F_{n+3}F_{n+4}}}\\&={\frac {11749}{5280}}-{\frac {60}{11}}\sum _{n=1}^{\infty }{\frac {(-1)^{n}}{F_{n}F_{n+1}F_{n+2}F_{n+3}F_{n+4}F_{n+5}F_{n+6}}}\end{aligned}}$

홀수 위치에서 피보나치 수의 역수의 합은 다음 값을 갖는다:

$\sum _{n=1}^{\infty }{\frac {1}{F_{2n-1}}}={\frac {\sqrt {5}}{\pi }}{\sqrt {\lambda ^{*}[16\operatorname {arsinh} (1/2)^{2}/\pi ^{2}]}}K\{\lambda ^{*}[16\operatorname {arsinh} (1/2)^{2}/\pi ^{2}]\}$

λ*은 모듈러 람다 함수이다.

K는 제 1 종 완전 타원 적분이다.

생성 함수

피보나치 수의 생성 함수는 다음과 같다.

$\sum _{n=0}^{\infty }F_{n}x^{n}={\frac {x}{1-x-x^{2}}}$

피보나치 수의 역수의 생성 함수는 다음과 같이 나타낼 수 있다.

${\begin{aligned}\sum _{n=1}^{\infty }{\frac {1}{F_{n}}}x^{n}&=\sum _{n=1}^{\infty }{\frac {x^{n}{\sqrt {5}}}{\varphi ^{n}}}+\sum _{n=1}^{\infty }(-1)^{n}{\frac {x^{n}}{F_{n}\varphi ^{2n}}}\\&={\frac {x{\sqrt {5}}}{\varphi -x}}+\sum _{n=1}^{\infty }(-1)^{n}{\frac {x^{n}}{F_{n}(F_{2n}\varphi +F_{2n-1})}}\\&={\frac {x{\sqrt {5}}}{\varphi -x}}-{\frac {x{\sqrt {5}}}{\varphi ^{3}+x}}+\sum _{n=1}^{\infty }{\frac {x^{n}}{F_{n}\varphi ^{4n}}}\\&={\frac {x{\sqrt {5}}}{\varphi -x}}-{\frac {x{\sqrt {5}}}{\varphi ^{3}+x}}+{\frac {x{\sqrt {5}}}{\varphi ^{5}-x}}+\sum _{n=1}^{\infty }(-1)^{n}{\frac {x^{n}}{F_{n}\varphi ^{6n}}}\end{aligned}}$

점근 공식

이웃하는 피보나치 수의 비

이웃하는 피보나치 수의 비는 황금비로 수렴한다.

$\lim _{n\to \infty }{\frac {F_{n+1}}{F_{n}}}=\varphi$

또한, 다음과 같은 부등식이 성립한다.

${\frac {\varphi ^{n-1/n}}{\sqrt {5}}}\leq F_{n}\leq {\frac {\varphi ^{n+1/n}}{\sqrt {5}}}$

수론적 성질

피보나치 수열은 서로 인접한 항끼리 서로소이다. 이는 귀납법으로 간단히 증명할 수 있다.

소스 코드

파이썬

피보나치 수열은 아래와 같이 함수의 재귀적 용법으로 구현할 수 있다.

def fib(n):
    if n == 0 or n == 1:
        return n

    return fib(n-2) + fib(n-1)

위 코드는 메모이제이션을 통해 성능을 개선할 수 있다.

memo = {}

def fib(n):
    if n == 0 or n == 1:
        return n

    if n not in memo:
        memo[n] = fib(n-2) + fib(n-1)

    return memo[n]

같이 보기

• 피보나치 수의 일반화
• 엠브리-트레페텐 상수
• 메모이제이션

외부 링크

• “Fibonacci numbers” (영어). 《Encyclopedia of Mathematics》. Springer-Verlag. 2001. ISBN 978-1-55608-010-4. 
• Weisstein, Eric Wolfgang. “Fibonacci number” (영어). 《Wolfram MathWorld》. Wolfram Research.