직관 논리
논리학에서 직관 논리(直觀論理, 영어: intuitionistic logic)는 수학적 직관주의에 근거하여 귀류법을 배척하는 논리 체계이다. 직관 논리에서 참인 모든 명제는 고전적으로도 참이지만 그 역은 일반적으로 성립하지 않는 특징이있다. 이처럼 직관주의 논리학은 이중부정의 일부법칙이 성립하지 않는다.
정의[편집]
직관 논리는 힐베르트 식으로 다음과 같이 서술되는 논리 체계이다.
통사론[편집]
직관 명제 논리에서, 명제 로부터 다음과 같은 새 명제들을 구성할 수 있다.
- 논리곱 . 이는 "이며 또한 "라고 읽는다.
- 논리합 . 이는 "이거나 또는 "라고 읽는다.
- 함의 . 이는 "만약 이라면 또한 성립한다"라고 읽는다.
- 거짓 . 이는 거짓 명제로 읽는다.
이들로부터 다음과 같은 기호들을 정의한다.
직관 술어 논리에서는 명제 논리 연산자 밖에도, 자유 변수 를 가지는 명제 로부터 다음과 같은 새 명제들을 구성할 수 있다.
- (존재 술어) . 이는 "를 성립시키는 가 존재한다"라고 읽는다.
- (보편 술어) . 이는 "모든 에 대하여, 가 성립한다"라고 읽는다.
추론[편집]
직관 명제 논리의 유일한 추론법은 전건 긍정의 형식이며, 이는 다음과 같다.
직관 술어 논리에서는 다음과 같은 두 변수 일반화 규칙이 추가된다. 여기서, 는 에서 자유 변수가 아닌 변수(한정 변수이거나, 아니면 에 등장하지 않는 변수)이다.
공리[편집]
직관 명제 논리의 공리들은 다음과 같다. 임의의 명제 에 대하여,
- (함의 조건의 추가)
- (함의의 분배)
- (논리곱의 좌측 제거)
- (논리곱의 우측 제거)
- (논리곱과 함의 조건의 추가)
- (논리합의 좌측 추가)
- (논리합의 우측 추가)
- (함의 조건들의 논리합)
- (거짓은 모든 명제를 함의)
직관 술어 논리에서는 다음 두 공리들이 추가로 성립한다. 여기서 는 에서 한정 변수가 아닌 변수이다.
- (보편 기호의 특수화)
- (존재 기호의 추가)
성질[편집]
명제의 격자[편집]
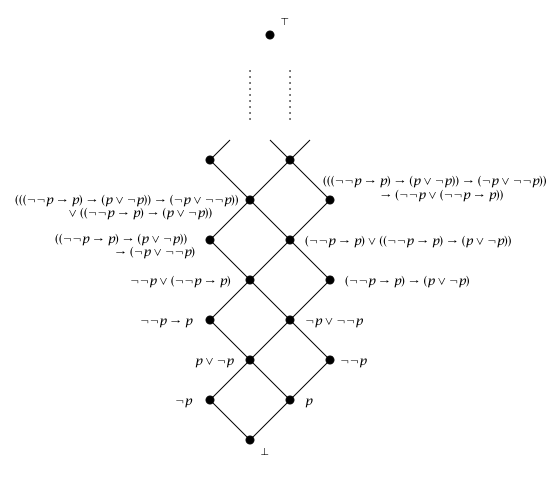
주어진 명제 로부터, 고전 명제 논리에서는 네 개의 명제밖에 정의할 수 없지만, 직관 명제 논리에서는 이로부터 무한한 수의, 서로 동치이지 않는 명제들이 존재한다. 이를 리에게르-니시무라 사다리(영어: Rieger–Nishimura ladder)라고 하며, 라디슬라프 스반테 리에게르(체코어: Ladislav Svante Rieger)[1]와 니시무라 이와오[2]가 정의하였다.
고전 논리와의 관계[편집]
직관 논리는 고전 논리의 일부분이다. 직관 논리에서 참인 모든 명제는 고전적으로도 참이지만, 고전적으로 참이지만 직관 논리에서는 증명할 수 없는 명제들이 존재한다. 이러한 명제들은 다음을 들 수 있다.
의미론[편집]
직관 논리의 경우, 다양한 의미론이 존재한다. 이 가운데 하나로는 다음과 같은 위상수학적 의미론을 생각할 수 있다. 어떤 위상 공간 에 대하여, 직관 논리를 다음과 같이 해석하자.
- 명제는 의 열린 집합에 대응한다.
- 논리합 는 합집합 에 대응한다.
- 논리곱 는 교집합 에 대응한다.
- 함의 는 교집합 에 대응한다. 여기서 는 집합의 내부이다.
- 거짓 은 공집합 이다.
이로부터 정의되는 부정과 동치는 다음과 같다.
일반적인 위상 공간에 대하여 증명할 수 있는 모든 명제들은 직관 논리에서 참임을 보일 수 있다.
이 밖에도, 양상 논리의 크립키 모형(영어: Kripke model)을 직관 논리에서도 사용할 수 있다.
역사[편집]
라위트전 브라우어르의 직관주의 수학을 형식화하기 위하여, 아런트 헤이팅이 도입하였다.
응용[편집]
직관 논리는 일반적인 토포스의 내부 논리(영어: internal logic)로 등장한다.[3] (표준적인) 집합의 토포스나, 이산 공간 위의 층의 토포스 등에서는 고전 논리가 성립하지만, 예를 들어 이산 공간이 아닌 위상 공간 위의 층의 토포스에서는 고전 논리가 성립하지 않고, 직관 논리를 사용해야만 한다.
참고 문헌[편집]
- ↑ Rieger, L. (1949). “On the lattice theory of Brouwerian propositional logics”. 《Spisy vydávané Přírodovědeckou fakultou University Karlovy》 (영어) 189: 1–40. MR 0040245.
- ↑ Nishimura, Iwao (1960년 12월). “On Formulas of One Variable in Intuitionistic Propositional Calculus”. 《The Journal of Symbolic Logic》 (영어) 25 (4): 327-331. doi:10.2307/2963526. JSTOR 2963526. MR 142456. Zbl 0108.00302.
- ↑ Mac Lane, Saunders; Ieke Moerdijk (1992). 《Sheaves in geometry and logic: a first introduction to topos theory》. Universitext (영어). Springer. doi:10.1007/978-1-4612-0927-0. ISBN 978-0-387-97710-2. ISSN 0172-5939. Zbl 0822.18001.
- 여훈근 (2000년 6월 17일). 《논리철학》. 인문사회과학총서 40. 고려대학교 출판부. ISBN 89-7641-409-8. 2016년 5월 28일에 원본 문서에서 보존된 문서. 2020년 1월 21일에 확인함.
- van Dalen, Dirk (2001년 8월). 〈Intuitionistic logic〉 (PDF). 《The Blackwell guide to philosophical logic》 (영어). Blackwell. 224–257쪽. doi:10.1111/b.9780631206934.2001.00014.x. ISBN 978-0-631-20693-4. Zbl 1002.03053.
- (직관주의 논리,한국수학사학회지 = The Korean journal for history of mathematics v.12 no.1 , 1999년, pp.32 - 44 이승온, 김혁수,, 박진원 , 이병식 )https://scienceon.kisti.re.kr/commons/util/originalView.do?cn=JAKO199911921897668&oCn=JAKO199911921897668&dbt=JAKO&journal=NJOU00294661
- (논리연구14-2(2011)pp.39~75 - 직관주의적 유형론에서의 명제와 판단, 정인교-KRF-2007-327-A00159)http://logicalkorea.com/attach/paper/14-2-ChungIK.pdf
외부 링크[편집]
- “Intuitionistic logic”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4.
- “Intuitionistic propositional calculus”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4.
- Moschovakis, Joan (2014년 5월 23일). “Intuitionistic logic”. 《Stanford Encyclopedia of Philosophy》 (영어).
- van Atten, Mark (2009년 4월 1일). “The development of intuitionistic logic”. 《Stanford Encyclopedia of Philosophy》 (영어).
- Iemhoff, Rosalie (2013년 8월 14일). “Intuitionism in the Philosophy of Mathematics”. 《Stanford Encyclopedia of Philosophy》 (영어).
- “Intuitionistic logic”. 《nLab》 (영어).