원 (기하학)

기하학에서 원(圓, 영어: circle)은 평면 위의 한 점에 이르는 거리가 일정한 평면 위의 점들의 집합으로 정의되는 도형이다. 이러한 점을 원의 중심이라고 하고, 중심과 원 위의 점을 잇는 선분 또는 이들의 공통된 길이를 원의 반지름이라고 한다.

원은 이차 곡선의 일종인 타원에서 이심률이 0인 경우이다.

용어

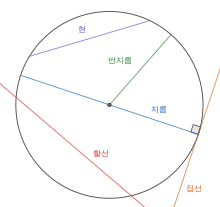
원과 관련된 기본적인 용어들은 다음과 같다.

단위원: 반지름이 1인 원
동심원: 중심이 같은 두 원
반원: 중심각이 평각인 부채꼴(활꼴)
반지름: 원의 중심과 그 원 위의 점을 잇는 선분 또는 그 선분의 길이. 반지름의 길이는 지름의 2분의 1이다.
부채꼴: 두 개의 반지름과 하나의 호로 둘러싸인 영역
사분원: 중심각이 직각인 부채꼴
원주: 원의 둘레
원주각: 한 끝점을 공유하는 두 현이 원 내부에서 이루는 각. 크기는 이에 대응하는 중심각의 1/2이다.
원판: 원으로 둘러싸인 도형
원환: 두 동심원으로 둘러싸인 도형
접선: 원과 한 점에서 만나는 직선
접현각: 원의 현과 현의 한 끝점에서의 접선이 이루는 각
중심: 원 위의 임의의 점에 이르는 거리가 일정한 그 원을 포함하는 평면 위의 점
중심각: 호의 두 끝점을 지나는 반지름이 호와 같은 쪽에서 이루는 각. 크기는 이에 대응하는 원주각의 2배이다.
지름: 원의 중심을 지나는 현 또는 그 길이. 길이는 반지름의 2배이다.
켤레호: 원의 합하여 원주 전체를 이루는 두 호
할선: 원과 두 점에서 만나는 직선
현: 원 위의 두 점을 잇는 선분
호: 원의 일부가 되는 곡선
활꼴: 같은 끝점을 갖는 호와 현으로 둘러싸인 영역
시: 할선의 중점을 수선의 발로 하는 선

역사

기원전 5세기경 안티폰은 정다각형의 변 수를 계속 늘려가면 결국엔 원이 된다고 생각했다. 이에 15세기 독일의 신학자 니콜라우스는 아무리 변을 늘려도 원이 될 수는 없다는 사상으로 반박했다.

해석적 성질

둘레와 넓이

어떤 원의 반지름의 길이를 $r$ 라고 하고, 지름의 길이를 $d$ 라고 하면, 원의 둘레는

C=2\pi r=\pi d

이다. 여기서 $\pi$ 는 원주율이다. 이는 약 3.1415…를 값으로 하는 초월수이다.

어떤 원의 반지름의 길이를 $r$ 라고 하고, 지름의 길이를 $d$ 라고 하고, 둘레를 $C$ 라고 하면, 원(으로 둘러싸인 도형)의 넓이는

A=\pi r^{2}={\frac {\pi d^{2}}{4}}={\frac {C^{2}}{4\pi }}

이다. 등주 부등식에 따르면, 이는 둘레가 $C$ 인 닫힌 곡선으로 둘러싸인 도형이 가질 수 있는 최대 넓이이다.

방정식

데카르트 좌표계

2차원 데카르트 좌표계 위의 중심이 $(a,b)$ 이고 반지름이 $r$ 인 원의 방정식은

(x-a)^{2}+(y-b)^{2}=r^{2}

이다.^[1]^{:22, §3} 이는 피타고라스 정리를 통해 유도된다.

2차원 데카르트 좌표계 위의 원의 방정식의 일반적인 꼴은

x^{2}+y^{2}+dx+ey+f=0

이다. 단, $d,e,f$ 는 실수이며,

d^{2}+e^{2}-f>0

이어야 한다.^[1]^{:23, §3.2} 좌변은 반지름의 4배에 대응하며, '=0'일 경우 한원소 집합이 되고, '<0'일 경우 공집합이 된다.^[1]^{:24, §3.2, Example 3.2}

평면 위의 모든 원은 적절한 데카르트 좌표계를 취했을 때

x^{2}+y^{2}=r^{2}

와 같은 표준적인 방정식으로 표현된다. 단, $r>0$ 이어야 한다. 이러한 꼴의 방정식을 얻으려면 원의 중심을 좌표계의 원점으로 삼기만 하면 된다.

2차원 데카르트 좌표계 위의 중심이 $(a,b)$ 이고 반지름이 $r$ 인 원은 다음과 같은 매개변수 방정식을 갖는다.^[1]^{:23, §3.2, (3.5)}

{\begin{matrix}x=a+r\cos t\\y=b+r\sin t\end{matrix}}\qquad (0\leq t<2\pi )

여기서 $\cos ,\sin$ 은 각각 코사인 함수와 사인 함수이고, $t$ 는 매개 변수이다.

극좌표계

데카르트 좌표 $(x,y)$ 대신 극좌표 $(r,\theta )$ 를 사용할 수도 있다. 즉, 극좌표계 위의 중심이 $(r_{0},\theta _{0})$ 이고 반지름이 $R$ 인 원의 방정식은

r^{2}-2rr_{0}\cos(\theta -\theta _{0})+r_{0}^{2}=R^{2}

이다.

복소평면

데카르트 좌표나 극좌표를 복소수 $z$ 로 대신하면, 원과 직선의 통일된 방정식을 얻을 수 있다.

복소평면 위에서, 중심이 $z_{0}$ 이고 반지름이 $r>0$ 인 원의 방정식은

|z-z_{0}|=r

이다. 여기서 $|\cdot |$ 는 복소수의 절댓값이다.

또한 복소평면 위의 원의 방정식의 일반적인 꼴은

Az{\bar {z}}+{\bar {B}}z+B{\bar {z}}+C=0

이다. 여기서 ${\bar {}}$ 는 켤레 복소수이다. 단, $A,C$ 는 실수이고, $B$ 는 복소수이며,

|B|^{2}-AC>0

A\neq 0

이어야 한다. 또한, $A\neq 0$ 대신 $A=0$ 을 취하고 다른 조건을 그대로 두면 복소평면 위의 직선의 방정식의 일반적인 꼴을 얻는다. 즉, $A\neq 0$ 이라는 조건을 제거하고 다른 조건을 그대로 두면 일반화 원의 방정식의 일반적인 꼴을 얻는다.

접선의 방정식

2차원 데카르트 좌표계 위에서, 원

(x-a)^{2}+(y-b)^{2}=r^{2}

의 $(x_{0},y_{0})$ 을 접점으로 하는 접선의 방정식은

(x_{0}-a)(x-a)+(y_{0}-b)(y-b)=r^{2}

이다.

원

(x-a)^{2}+(y-b)^{2}=r^{2}

의 기울기가 $m$ 인 접선의 방정식은

y-b=m(x-a)\pm r{\sqrt {m^{2}+1}}

이다.

기하적 성질

대칭

원은 지름에 대한 반사와 원의 중심에 대한 회전에 대하여 대칭이다.^[2]^{:227, §20.1, Theorem 20.3}
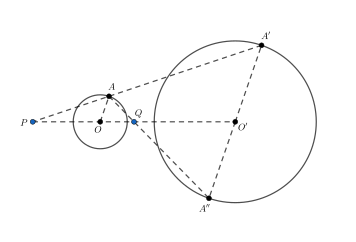
- 즉, 원의 대칭군은 2차원 직교군 $\operatorname {O} (2,\mathbb {R} )$ 이다.
임의의 두 원은 서로 중심 닮음이며, 동심원이 아닐 경우 두 원의 중심을 잇는 선분의 반지름의 비에 따른 내분점 및 외분점을 닮음 중심으로 갖는다.^[3]^{:19, §25}

반지름의 길이가 같은 모든 원은 서로 합동이다.^[4]^{:23, §1F}
공선점이 아닌 세 점을 지나는 원은 항상 유일하게 존재한다.^[4]^{:23, §1F, Theorem 1.15}
- 즉, 모든 삼각형의 외접원은 유일하게 존재한다.
- 즉, 임의의 세 점을 지나는 일반화 원은 항상 유일하게 존재한다.

호와 현

현의 수직 이등분선은 원의 중심을 지난다.^[2]^{:227, §20.1, Theorem 20.2}
- 즉, 현에 수직인 지름은 현을 이등분한다.^[2]^{:227, §20.1, Theorem 20.2}
- 즉, 지름이 아닌 현을 이등분하는 지름은 현에 수직이다.^[2]^{:227, §20.1, Theorem 20.2}
지름은 원의 가장 긴 현이다.^[4]^{:23, §1F}
(방멱 정리) 원 위에 있지 않은 점 $P$ 를 지나는 두 직선 가운데 하나는 원과 점 $A$ 와 $B$ 에서 만나고, 다른 하나는 원과 점 $C$ 와 $D$ 에서 만난다고 하면, $PA\cdot PB=PC\cdot PD$ 이다.^[4]^{:47, §1H, Theorem 1.35}
원 위의 점과 현 사이의 거리와 지름의 곱은 점과 현의 양 끝점 사이의 거리의 곱과 같다.^[3]^{:71, §101}

원과 직선의 위치 관계

평면 위의 원과 직선의 위치 관계는 원의 중심에서 직선까지의 거리 $d$ 와 원의 반지름 $r$ 의 대소 관계에 따라 다음과 같은 경우로 나뉜다.

만약 $d>r$ 라면, 원과 직선은 만나지 않는다.
만약 $d=r$ 라면, 원과 직선은 한 점에서 만난다. 즉, 직선은 원의 접선이다.
만약 $d<r$ 라면, 원과 직선은 두 점에서 만난다. 즉, 직선은 원의 할선이다.

두 원의 위치 관계

두 원의 위치 관계는 두 원의 반지름 $R,r$ 와 두 중심 사이의 거리 $d$ 에 따라 다음과 같은 경우로 나뉜다.

만약 $d>R+r$ $d>R+r$ 이거나 $d<|R-r|$ $d<|R-r|$ 라면, 두 원은 만나지 않는다.
- 만약 $d>R+r$ 라면, 두 원은 서로의 외부에 놓이며, 교점을 가지지 않는다.
- 만약 $d<|R-r|$ 라면, 작은 원은 큰 원의 내부에 놓이며, 교점을 가지지 않는다.
만약 $d=R+r$ $d=R+r$ 이거나 $d=|R-r|$ $d=|R-r|$ 라면, 두 원은 한 점에서 만난다. 즉, 두 원은 서로 접한다.
- 만약 $d=R+r$ 라면, 두 원은 서로의 외부에서 접한다. 즉, 두 원은 외접한다.
- 만약 $d=|R-r|$ 라면, 작은 원이 큰 원의 내부에서 큰 원에 접한다. 즉, 두 원은 내접한다.
만약 $|R-r|<d<R+r$ 라면, 두 원은 두 점에서 만난다.

중심각과 원주각

주어진 호에 대한 원주각의 크기는 그 호에 대한 중심각의 1/2이다.^[4]^{:25, §1F, Theorem 1.16}
같은 호에 대한 두 원주각의 크기는 서로 같다.^[4]^{:25, §1F}
켤레호에 대한 두 중심각은 서로 보각이다.
- 즉, 내접 사각형의 두 대각은 서로 보각이다.^[4]^{:26, §1F, Corollary 1.17}
- 즉, 내접 사각형의 외각의 크기는 내대각과 같다.

(탈레스 정리) 지름에 대한 원주각은 직각이다.
- 즉, 삼각형의 외심이 변 위에 있을 필요충분조건은 직각 삼각형이다.^[4]^{:30, §1F, Corollary 1.22}
원의 두 현이 원 내부에서 이루는 각의 크기는 이 각과 맞꼭지각의 내부에 포함되는 두 호에 대한 중심각의 합의 1/2이다.^[4]^{:27, §1F, Corollary 1.19}
원의 두 할선이 원 외부에서 이루는 각의 크기는 이 각의 내부에 포함되는 두 호에 대한 중심각의 차의 1/2이다.^[4]^{:27, §1F, Corollary 1.18}

접선

원 위의 한 점을 지나는 원의 접선은 유일하게 존재하고, 이는 이 점을 지나는 반지름에 수직이다.^[2]^{:228, §20.1, Theorem 20.4}^[4]^{:30-31, §1F}
- 즉, 반지름의 반지름 끝점에서의 수선은 원에 접한다.^[2]^{:228, §20.1, Theorem 20.4}
- 즉, 원의 접선의 접점에서의 수선은 원의 중심을 지난다.
원 외부의 한 점을 지나는 원의 접선은 정확히 2개이고, 이 점과 두 접점 사이의 거리는 같으며, 두 접선이 이루는 각과 두 접점을 지나는 반지름이 이루는 각은 서로 보각이다.
원의 접현각의 크기는 현을 기준으로 이와 같은 쪽에 있는 호에 대한 중심각의 1/2이다.^[4]^{:31, §1F, Theorem 1.23}
원의 접선과 할선이 원 외부에서 이루는 각은 각의 내부에 포함된 두 호의 중심각의 차의 1/2이다.^[4]^{:31, §1F, Corollary 1.24}
외접하는 두 원의 교점을 지나는 두 공통 할선 사이의 두 현은 서로 평행한다.^[4]^{:31, §1F, Problem 1.25}
(접선에 대한 방멱 정리)원 외부의 점 $P$ 를 지나는 두 직선 가운데 하나는 원과 $A$ 와 $B$ 에서 만나고, 하나는 원에 점 $T$ 에서 접한다고 하면, $PA\cdot PB=PT^{2}$ 이다.

원의 직교

두 원의 교점에서의 두 접선이 서로 수직일 경우 두 원이 서로 직교한다고 한다.^[3]^{:33, §48}
두 원의 반지름이 $r,r'$ 이고, 두 중심 사이의 거리가 $d$ 라고 할 때, 두 원이 서로 직교할 필요충분조건은 $r^{2}+{r'}^{2}=d^{2}$ 이다.^[3]^{:34, §48}
주어진 원에 직교하고 중심이 원 외부의 주어진 점인 원은 유일하게 존재한다.^[3]^{:34, §48}
주어진 원에 직교하고 원의 지름이 아닌 현의 두 끝점을 지나는 원은 유일하게 존재한다.^[3]^{:34, §48}

작도

공선점이 아닌 세 점을 지나는 원

공선점이 아닌 세 점 $A,B,C$ 를 지나는 원은 컴퍼스와 자를 사용하여 다음과 같이 작도할 수 있다.

선분 $AB$ 의 수직 이등분선을 그린다.
선분 $BC$ 의 수직 이등분선을 그린다.
선분 $AB$ 와 $BC$ 의 교점 $O$ 를 취한다.
점 $O$ 를 중심으로 하고 선분 $OA$ 를 반지름으로 하는 원을 그린다. 이 경우 원은 점 $A,B,C$ 를 지난다.

원의 중심

주어진 원의 중심은 컴퍼스와 자를 사용하여 다음과 같이 작도할 수 있다.

원 위의 두 점 $A,B$ 을 취한다.
선분 $AB$ 의 점 $B$ 에서의 수선 $BP$ 를 그린다.
직선 $BP$ 와 원의 교점 $C$ 를 취한다. 이 경우 선분 $AC$ 는 원의 지름이다.
또 다른 지름 $A'C'$ 을 작도한다.
선분 $AC$ 와 $A'C'$ 의 교점 $O$ 를 취한다. 이 경우 점 $O$ 는 원의 중심이다.

원적 문제

원적 문제는 주어진 원과 넓이가 같은 정사각형을 컴퍼스와 자로 작도하는 문제를 일컫는다. 이는 원주율 $\pi$ 가 초월수이므로 불가능하다.

기타 관련 주제

내접원, 외접원, 방접원

모든 삼각형은 유일한 내접원 및 외접원과 정확히 3개의 방접원을 갖는다. 그러나, 일반적으로 다각형은 내접원이나 외접원을 가질 필요가 없다. 어떤 다각형이 모든 변에 접하는 원을 가질 경우, 이 다각형을 외접 다각형이라고 한다. 어떤 다각형이 모든 꼭짓점을 지나는 원을 가질 경우, 이 다각형을 내접 다각형이라고 한다. 동시에 외접 다각형이며 내접 다각형인 다각형을 이중중심 다각형이라고 한다. 예를 들어, 모든 삼각형과 모든 정다각형은 이중중심 다각형이다.

주어진 원의 내접 $n$ 각형 가운데 넓이가 가장 큰 것은 정 $n$ 각형이다.^[4]^{:35, §1G}

문학

에드윈 A. 애보트의 공상 수학 소설 《플랫랜드》에서는 원이 성직자로 출현하며, 평면도형들 중 가장 고귀한 계급으로 여겨진다.

같이 보기

각주

↑ ^가 ^나 ^다 ^라 Gibson, C. G. (2003). 《Elementary Euclidean geometry》 (영어). Cambridge: Cambridge University Press. ISBN 978-0-521-83448-3.
↑ ^가 ^나 ^다 ^라 ^마 ^바 Martin, George E. (1975). 《The Foundations of Geometry and the Non-Euclidean Plane》. Undergraduate Texts in Mathematics (영어). New York, NY: Springer. doi:10.1007/978-1-4612-5725-7. ISBN 978-1-4612-5727-1.
↑ ^가 ^나 ^다 ^라 ^마 ^바 Johnson, Roger A. (1960) [1929]. 《Advanced Euclidean Geometry》 (영어). New York, N. Y.: Dover Publications.
↑ ^가 ^나 ^다 ^라 ^마 ^바 ^사 ^아 ^자 ^차 ^카 ^타 ^파 ^하 ^거 Isaacs, I. Martin (2001). 《Geometry for College Students》. The Brooks/Cole Series in Advanced Mathematics (영어). Brooks/Cole. ISBN 0-534-35179-4.

외부 링크

위키미디어 공용에 원 관련 미디어 분류가 있습니다.

[Gibson-1] 가 ^나 ^다 ^라 Gibson, C. G. (2003). 《Elementary Euclidean geometry》 (영어). Cambridge: Cambridge University Press. ISBN 978-0-521-83448-3.

[Martin-2] 가 ^나 ^다 ^라 ^마 ^바 Martin, George E. (1975). 《The Foundations of Geometry and the Non-Euclidean Plane》. Undergraduate Texts in Mathematics (영어). New York, NY: Springer. doi:10.1007/978-1-4612-5725-7. ISBN 978-1-4612-5727-1.

[Johnson-3] 가 ^나 ^다 ^라 ^마 ^바 Johnson, Roger A. (1960) [1929]. 《Advanced Euclidean Geometry》 (영어). New York, N. Y.: Dover Publications.

[Isaacs-4] 가 ^나 ^다 ^라 ^마 ^바 ^사 ^아 ^자 ^차 ^카 ^타 ^파 ^하 ^거 Isaacs, I. Martin (2001). 《Geometry for College Students》. The Brooks/Cole Series in Advanced Mathematics (영어). Brooks/Cole. ISBN 0-534-35179-4.

[1]

[2]

[3]

[4]