순서론 에서, 격자 (格子, 영어 : lattice )는 부분 순서 집합 의 하나로, 해당 집합의 임의의 두 원소로 이루어진 부분집합에 대해 항상 상한과 하한 이 존재하는 부분 순서 집합 이다. 다시 말해서, 부분 순서 집합 (S,
≤
{\displaystyle \leq }
≤
{\displaystyle \leq }
≤
{\displaystyle \leq }
≤
{\displaystyle \leq }
≤
{\displaystyle \leq }
정의 격자의 개념은 추상대수학 적으로 또는 순서론 적으로 정의할 수 있으며, 이 두 정의는 서로 동치 이다.
대수학적 정의 격자
(
L
,
∨
,
∧
)
{\displaystyle (L,\vee ,\wedge )}
이항연산
∨
,
∧
:
L
×
L
→
L
{\displaystyle \vee ,\wedge \colon L\times L\to L}
대수 구조 이다. 여기서
∨
{\displaystyle \vee }
이음 (영어 : join 조인[* ] ),
∧
{\displaystyle \wedge }
만남 (영어 : meet 미트[* ] )이라고 한다. 모든
a
,
b
,
c
∈
L
{\displaystyle a,b,c\in L}
(교환법칙 )
a
∨
b
=
b
∨
a
{\displaystyle a\vee b=b\vee a}
a
∧
b
=
b
∧
a
{\displaystyle a\wedge b=b\wedge a}
(결합법칙 )
(
a
∨
b
)
∨
c
=
a
∨
(
b
∨
c
)
{\displaystyle (a\vee b)\vee c=a\vee (b\vee c)}
(
a
∧
b
)
∧
c
=
a
∧
(
b
∧
c
)
{\displaystyle (a\wedge b)\wedge c=a\wedge (b\wedge c)}
(흡수법칙)
a
∨
(
a
∧
b
)
=
a
∧
(
a
∨
b
)
=
a
{\displaystyle a\vee (a\wedge b)=a\wedge (a\vee b)=a}
이로부터 다음을 증명할 수 있다.
(멱등성)
a
∧
a
=
a
∨
a
=
a
{\displaystyle a\wedge a=a\vee a=a}
멱등성의 증명
흡수법칙을 두 번 사용하면 다음과 같다.
a
∧
a
=
a
∧
(
a
∨
(
a
∧
a
)
)
=
a
{\displaystyle a\wedge a=a\wedge (a\vee (a\wedge a))=a}
a
∨
a
=
a
∨
(
a
∧
(
a
∨
a
)
)
=
a
{\displaystyle a\vee a=a\vee (a\wedge (a\vee a))=a}
격자
(
L
,
∨
,
∧
)
{\displaystyle (L,\vee ,\wedge )}
부분 순서
≤
{\displaystyle \leq }
a
≤
b
⟺
a
=
a
∧
b
⟺
b
=
a
∨
b
{\displaystyle a\leq b\iff a=a\wedge b\iff b=a\vee b}
(이 두 성질은 흡수법칙에 따라 동등하다.)
순서론적 정의 다음 성질을 만족시키는 부분 순서 집합
(
L
,
≤
)
{\displaystyle (L,\leq )}
격자 라고 한다.
(이음의 존재) 모든
a
,
b
∈
L
{\displaystyle a,b\in L}
{
a
,
b
}
{\displaystyle \{a,b\}}
상한
a
∨
b
∈
L
{\displaystyle a\vee b\in L}
이음 (영어 : join 조인[* ] )이라고 한다. 즉, 이는 다음을 만족시킨다.
a
,
b
≤
a
∨
b
{\displaystyle a,b\leq a\vee b}
a
,
b
≤
c
⟹
a
∨
b
≤
c
{\displaystyle a,b\leq c\implies a\vee b\leq c}
(이음의 존재) 모든
a
,
b
∈
L
{\displaystyle a,b\in L}
{
a
,
b
}
{\displaystyle \{a,b\}}
하한
a
∧
b
∈
L
{\displaystyle a\wedge b\in L}
만남 (영어 : meet 미트[* ] )이라고 한다. 즉, 이는 다음을 만족시킨다.
a
∧
b
≤
a
,
b
{\displaystyle a\wedge b\leq a,b}
c
≤
a
,
b
⟹
c
≤
a
∧
b
{\displaystyle c\leq a,b\implies c\leq a\wedge b}
이음과 만남이 유일함을 쉽게 보일 수 있다.
격자 준동형사상 격자 준동형사상이 아닌 증가함수.
u
∨
v
=
1
{\displaystyle u\vee v=1}
u
′
∨
u
′
=
u
′
≠
1
′
{\displaystyle u'\vee u'=u'\neq 1'}
두 격자
L
,
L
′
{\displaystyle L,L'}
격자 준동형사상 (영어 : lattice homomorphism )은 이음과 만남을 보존하는 사상
ϕ
:
L
→
L
′
{\displaystyle \phi \colon L\to L'}
a
,
b
∈
L
{\displaystyle a,b\in L}
ϕ
(
a
)
∧
ϕ
(
b
)
=
ϕ
(
a
∧
b
)
{\displaystyle \phi (a)\wedge \phi (b)=\phi (a\wedge b)}
ϕ
(
a
)
∨
ϕ
(
b
)
=
ϕ
(
a
∨
b
)
{\displaystyle \phi (a)\vee \phi (b)=\phi (a\vee b)}
이 경우, 만약
a
≤
b
{\displaystyle a\leq b}
ϕ
(
a
)
≤
ϕ
(
b
)
{\displaystyle \phi (a)\leq \phi (b)}
증가함수 이다. 반면, 증가함수이지만 격자 준동형사상이 아닌 함수도 존재한다.
반대 격자 주어진 격자
(
L
,
≤
L
,
∧
L
,
∨
L
)
{\displaystyle (L,\leq _{L},\wedge _{L},\vee _{L})}
반대 격자 (영어 : opposite lattice )
L
op
{\displaystyle L^{\operatorname {op} }}
L
{\displaystyle L}
a
,
b
∈
L
{\displaystyle a,b\in L}
a
∨
L
op
b
=
a
∧
L
b
{\displaystyle a\vee _{L^{\operatorname {op} }}b=a\wedge _{L}b}
a
∧
L
op
b
=
a
∨
L
b
{\displaystyle a\wedge _{L^{\operatorname {op} }}b=a\vee _{L}b}
a
≤
L
op
b
=
a
≥
L
b
{\displaystyle a\leq _{L^{\operatorname {op} }}b=a\geq _{L}b}
즉, 부분 순서 가 반대 방향이 되고, 만남과 이음이 서로 치환된다.
예 전순서 전순서 집합
(
T
,
≤
)
{\displaystyle (T,\leq )}
a
∨
b
=
max
{
a
,
b
}
{\displaystyle a\vee b=\max\{a,b\}}
a
∧
b
=
min
{
a
,
b
}
{\displaystyle a\wedge b=\min\{a,b\}}
이다.
부분집합 격자 세 원소를 가진 집합의 부분집합의 격자 집합
S
{\displaystyle S}
멱집합
P
(
S
)
=
{
A
⊂
S
}
{\displaystyle {\mathcal {P}}(S)=\{A\subset S\}}
⊂
{\displaystyle \subset }
부분 순서 집합 을 이룬다. 이 부분 순서 집합은 격자를 이루며, 이 경우 집합 S 의 어떤 두 부분 집합의 이음과 만남은 각각 두 부분 집합의 합집합 과 교집합 이다.
A
⊂
B
⟺
A
≤
B
{\displaystyle A\subset B\iff A\leq B}
A
∪
B
=
A
∨
B
{\displaystyle A\cup B=A\vee B}
A
∩
B
=
A
∧
B
{\displaystyle A\cap B=A\wedge B}
마찬가지로,
S
{\displaystyle S}
{
A
⊂
S
:
|
A
|
<
ℵ
0
}
{\displaystyle \{A\subset S\colon |A|<\aleph _{0}\}}
약수의 격자 60의 약수들의 격자 양의 정수
n
{\displaystyle n}
n
{\displaystyle n}
Z
+
{\displaystyle \mathbb {Z} ^{+}}
정수론
격자
a
∣
b
{\displaystyle a\mid b}
a
≤
b
{\displaystyle a\leq b}
lcm
(
a
,
b
)
{\displaystyle \operatorname {lcm} (a,b)}
최소공배수 )
a
∨
b
{\displaystyle a\vee b}
gcd
(
a
,
b
)
{\displaystyle \gcd(a,b)}
최대공약수 )
a
∧
b
{\displaystyle a\wedge b}
이는 환
Z
/
n
{\displaystyle \mathbb {Z} /n}
Z
{\displaystyle \mathbb {Z} }
아이디얼 들의 격자의 특수한 경우이다.
분할 격자 집합
S
{\displaystyle S}
분할
P
⊂
P
(
S
)
{\displaystyle P\subset {\mathcal {P}}(S)}
분할
격자
분할의 세분
∀
p
∈
P
:
∃
q
⊂
Q
:
p
⊂
q
{\displaystyle \forall p\in P\colon \exists q\subset Q\colon p\subset q}
P
≤
Q
{\displaystyle P\leq Q}
공통 세분
{
p
∩
q
|
p
∈
Q
,
q
∈
Q
}
{\displaystyle \{p\cap q|p\in Q,q\in Q\}}
P
∧
Q
{\displaystyle P\wedge Q}
공통 역세분
max
{
R
|
R
≥
P
,
Q
}
{\displaystyle \max\{R|R\geq P,Q\}}
P
∨
Q
{\displaystyle P\vee Q}
열린 집합의 격자 위상 공간
X
{\displaystyle X}
완비 헤이팅 대수 이다.
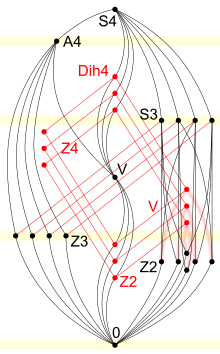
대수학에서의 격자 대칭군
S
4
{\displaystyle S_{4}}
군
G
{\displaystyle G}
부분군
격자
H
⊂
H
′
{\displaystyle H\subset H'}
H
≤
H
′
{\displaystyle H\leq H'}
H
∩
H
′
{\displaystyle H\cap H'}
H
∧
H
′
{\displaystyle H\wedge H'}
⟨
H
∪
H
′
⟩
{\displaystyle \langle H\cup H'\rangle }
H
∪
H
′
{\displaystyle H\cup H'}
H
∨
H
′
{\displaystyle H\vee H'}
1 (자명군 )
⊥
{\displaystyle \bot }
G
{\displaystyle G}
⊤
{\displaystyle \top }
마찬가지로, 주어진 군의 정규부분군 들 역시 완비 모듈러 격자 를 이룬다.
유사환
R
{\displaystyle R}
아이디얼 들의 집합
Ideal
(
R
)
{\displaystyle \operatorname {Ideal} (R)}
완비 격자 를 이룬다.
아이디얼
격자
a
⊂
b
{\displaystyle {\mathfrak {a}}\subset {\mathfrak {b}}}
a
≤
b
{\displaystyle {\mathfrak {a}}\leq {\mathfrak {b}}}
a
∩
b
{\displaystyle {\mathfrak {a}}\cap {\mathfrak {b}}}
a
∧
b
{\displaystyle {\mathfrak {a}}\wedge {\mathfrak {b}}}
a
+
b
{\displaystyle {\mathfrak {a}}+{\mathfrak {b}}}
a
∨
b
{\displaystyle {\mathfrak {a}}\vee {\mathfrak {b}}}
{
0
}
{\displaystyle \{0\}}
⊥
{\displaystyle \bot }
R
{\displaystyle R}
⊤
{\displaystyle \top }
벡터 공간
V
{\displaystyle V}
완비 격자 를 이룬다. 이 격자는 양자 논리 의 기반을 이룬다.
벡터 공간
격자
A
⊂
B
{\displaystyle A\subset B}
A
≤
B
{\displaystyle A\leq B}
A
∩
B
{\displaystyle A\cap B}
A
∧
B
{\displaystyle A\wedge B}
span
(
A
,
B
)
{\displaystyle \operatorname {span} (A,B)}
A
∨
B
{\displaystyle A\vee B}
{
0
}
{\displaystyle \{0\}}
⊥
{\displaystyle \bot }
V
{\displaystyle V}
⊤
{\displaystyle \top }
참고 문헌 Donnellan, Thomas (1968). 《Lattice theory》. Pergamon. Zbl 0194.32503 . Grätzer, G. (1971). 《Lattice theory: first concepts and distributive lattices》. A Series of Books in Mathematics. W. H. Freeman. Zbl 0232.06001 . Davey, B.A.; H. A. Priestley (2002). 《Introduction to lattices and order》 2판. Cambridge University Press. doi :10.1017/CBO9780511809088 . ISBN 978-0-521-78451-1 Zbl 1002.06001 . Birkhoff, Garrett (1967). 《Lattice theory》. AMS Colloquium Publications 25 3판. American Mathematical Society. Dilworth, Robert P.; Peter Crawley (1973). 《Algebraic theory of lattices》. Prentice-Hall. ISBN 978-0-13-022269-5 Johnstone, Peter T. (1983년 4월). 《Stone spaces》 . Cambridge Studies in Advanced Mathematics 3 . Cambridge University Press. ISBN 978-052123893-9 MR 0698074 . Zbl 0499.54001 . Bilová, Štěpánka (2001). 〈Lattice theory — its birth and life〉 . Eduard Fuchs. 《Mathematics throughout the ages. Contributions from the summer school and seminars on the history of mathematics and from the 10th and 11th Novembertagung on the history and philosophy of mathematics, Holbaek, Denmark, October 28-31, 1999, and Brno, the Czech Republic, November 2-5, 2000》. Prometheus. 250–257쪽. ISBN 80-7196-219-8 Zbl 1009.01014 . Rota, Gian-Carlo (1977년 12월). “The Many Lives of Lattice Theory” (PDF) . 《Notices of the American Mathematical Society》 44 (11): 1440–1445. Zbl 0908.06001 . 바깥 고리