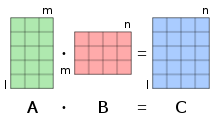
행렬 곱셈을 위해선 첫째 행렬의 열 갯수와 둘째 행렬의 행 갯수가 동일해야한다. 곱셈의 결과 새롭게 만들어진 행렬은 첫째 행렬의 행 갯수와 둘째 행렬의 열 갯수를 가진다. 행렬 곱셈 (matrix multiplication )은 두 개의 행렬 에서 한 개의 행렬을 만들어내는 이항연산 이다. 이 때 첫째 행렬의 열 개수와 둘째 행렬의 행 개수가 동일해야한다. 곱셈의 결과 새롭게 만들어진 행렬은 행렬곱 (matrix product)라 하며, 첫째 행렬의 행 개수와 둘째 행렬의 열 개수를 가진다. 행렬
A
{\displaystyle A}
B
{\displaystyle B}
A
B
{\displaystyle AB}
[ 1] [ 2]
벡터의 선형결합 또는 선형사상 의 합성 등의 의미를 부여할 수 있다.
행렬 곱셈은 1812년 프랑스의 수학자 자크 비네 가 선형 변환 의 합성 을 표현하고자 처음으로 사용하였다.[ 3] 선형대수학 의 기초가 되어 수학 , 통계학 , 물리학 , 경제학 , 공학 , 컴퓨터 프로그래밍 등의 분야에서 다양하게 응용되고 있다.[ 4] [ 5]
이 문서에서는 행렬을 굵은 대문자로(A 벡터 를 굵은 소문자로(a A a 첨자표기법 은 가장 일반적인 방식을 따라 행렬 A i j (A )ij , A ij a ij A 1 , A 2
A B m × n n × p
A
=
(
a
11
a
12
⋯
a
1
n
a
21
a
22
⋯
a
2
n
⋮
⋮
⋱
⋮
a
m
1
a
m
2
⋯
a
m
n
)
,
B
=
(
b
11
b
12
⋯
b
1
p
b
21
b
22
⋯
b
2
p
⋮
⋮
⋱
⋮
b
n
1
b
n
2
⋯
b
n
p
)
{\displaystyle \mathbf {A} ={\begin{pmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\\\end{pmatrix}},\quad \mathbf {B} ={\begin{pmatrix}b_{11}&b_{12}&\cdots &b_{1p}\\b_{21}&b_{22}&\cdots &b_{2p}\\\vdots &\vdots &\ddots &\vdots \\b_{n1}&b_{n2}&\cdots &b_{np}\\\end{pmatrix}}}
행렬곱 C = AB m × p [ 6] [ 7] [ 8] [ 9]
C
=
(
c
11
c
12
⋯
c
1
p
c
21
c
22
⋯
c
2
p
⋮
⋮
⋱
⋮
c
m
1
c
m
2
⋯
c
m
p
)
{\displaystyle \mathbf {C} ={\begin{pmatrix}c_{11}&c_{12}&\cdots &c_{1p}\\c_{21}&c_{22}&\cdots &c_{2p}\\\vdots &\vdots &\ddots &\vdots \\c_{m1}&c_{m2}&\cdots &c_{mp}\\\end{pmatrix}}}
이 때 i = 1, ..., m j = 1, ..., p C
c
i
j
=
a
i
1
b
1
j
+
a
i
2
b
2
j
+
⋯
+
a
i
n
b
n
j
=
∑
k
=
1
n
a
i
k
b
k
j
,
{\displaystyle c_{ij}=a_{i1}b_{1j}+a_{i2}b_{2j}+\cdots +a_{in}b_{nj}=\sum _{k=1}^{n}a_{ik}b_{kj},}
이는 곧 A i 번째 행과 B j 번째 열의 성분들을 각각 곱해 더한 것과 같은데, 달리 말하면 A i 번째 행과 B j 번째 열의 스칼라곱 인 것이다.[ 10]
그런고로 AB
C
=
(
a
11
b
11
+
⋯
+
a
1
n
b
n
1
a
11
b
12
+
⋯
+
a
1
n
b
n
2
⋯
a
11
b
1
p
+
⋯
+
a
1
n
b
n
p
a
21
b
11
+
⋯
+
a
2
n
b
n
1
a
21
b
12
+
⋯
+
a
2
n
b
n
2
⋯
a
21
b
1
p
+
⋯
+
a
2
n
b
n
p
⋮
⋮
⋱
⋮
a
m
1
b
11
+
⋯
+
a
m
n
b
n
1
a
m
1
b
12
+
⋯
+
a
m
n
b
n
2
⋯
a
m
1
b
1
p
+
⋯
+
a
m
n
b
n
p
)
{\displaystyle \mathbf {C} ={\begin{pmatrix}a_{11}b_{11}+\cdots +a_{1n}b_{n1}&a_{11}b_{12}+\cdots +a_{1n}b_{n2}&\cdots &a_{11}b_{1p}+\cdots +a_{1n}b_{np}\\a_{21}b_{11}+\cdots +a_{2n}b_{n1}&a_{21}b_{12}+\cdots +a_{2n}b_{n2}&\cdots &a_{21}b_{1p}+\cdots +a_{2n}b_{np}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}b_{11}+\cdots +a_{mn}b_{n1}&a_{m1}b_{12}+\cdots +a_{mn}b_{n2}&\cdots &a_{m1}b_{1p}+\cdots +a_{mn}b_{np}\\\end{pmatrix}}}
이러한 이유로 첫째 행렬의 열 갯수와 둘째 행렬의 행 갯수가 동일해야 행렬곱이 정의될 수 있는 것이다.[ 11]
대부분의 경우 행렬의 성분은 숫자이지만, 덧셈 과 곱셈 이 정의되고, 곱셈의 결합법칙 과 덧셈의 교환법칙 이 성립하여 곱셈의 분배법칙 이 성립하게 되는 다른 수학적 대상 들도 성분이 될 수 있다. 가장 대표적인 예시로 성분이 행렬인 블록 행렬 을 생각할 수 있다.
첫째 행렬의 행과 둘째 행렬의 열이 만나 행렬곱의 성분이 형성된다. 오른쪽 그림은 두 행렬 A B A B
[
a
11
a
12
⋅
⋅
a
31
a
32
⋅
⋅
]
4
×
2
matrix
[
⋅
b
12
b
13
⋅
b
22
b
23
]
2
×
3
matrix
=
[
⋅
c
12
⋅
⋅
⋅
⋅
⋅
⋅
c
33
⋅
⋅
⋅
]
4
×
3
matrix
{\displaystyle {\overset {4\times 2{\text{ matrix}}}{\begin{bmatrix}a_{11}&a_{12}\\\cdot &\cdot \\a_{31}&a_{32}\\\cdot &\cdot \\\end{bmatrix}}}{\overset {2\times 3{\text{ matrix}}}{\begin{bmatrix}\cdot &b_{12}&b_{13}\\\cdot &b_{22}&b_{23}\\\end{bmatrix}}}={\overset {4\times 3{\text{ matrix}}}{\begin{bmatrix}\cdot &c_{12}&\cdot \\\cdot &\cdot &\cdot \\\cdot &\cdot &c_{33}\\\cdot &\cdot &\cdot \\\end{bmatrix}}}}
오른쪽 그림에서 원으로 표시된 교차점의 값은 다음과 같다:
c
12
=
a
11
b
12
+
a
12
b
22
c
33
=
a
31
b
13
+
a
32
b
23
.
{\displaystyle {\begin{aligned}c_{12}&=a_{11}b_{12}+a_{12}b_{22}\\c_{33}&=a_{31}b_{13}+a_{32}b_{23}.\end{aligned}}}
선형대수학 적 계산을 행렬 곱셈을 통해 더욱 간단하게 할 수 있는데, 물리학 , 공학 , 컴퓨터 과학 분야에서 특히 빛을 발한다.
n 열 벡터
x
=
(
x
1
x
2
⋮
x
n
)
{\displaystyle \mathbf {x} ={\begin{pmatrix}x_{1}\\x_{2}\\\vdots \\x_{n}\end{pmatrix}}}
를 n 선형 변환 한 것을
y
=
A
(
x
)
=
(
a
11
x
1
+
⋯
+
a
1
n
x
n
a
21
x
1
+
⋯
+
a
2
n
x
n
⋮
a
m
1
x
1
+
⋯
+
a
m
n
x
n
)
{\displaystyle \mathbf {y} =A(\mathbf {x} )={\begin{pmatrix}a_{11}x_{1}+\cdots +a_{1n}x_{n}\\a_{21}x_{1}+\cdots +a_{2n}x_{n}\\\vdots \\a_{m1}x_{1}+\cdots +a_{mn}x_{n}\end{pmatrix}}}
라 하자. 이 때 선형 변환 A
A
=
(
a
11
a
12
⋯
a
1
n
a
21
a
22
⋯
a
2
n
⋮
⋮
⋱
⋮
a
m
1
a
m
2
⋯
a
m
n
)
{\displaystyle \mathbf {A} ={\begin{pmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\\\end{pmatrix}}}
이제 행렬을 사용해 선형변환을 표현하면 다음과 같이 나타낼 수 있다.
y
=
A
x
{\displaystyle \mathbf {y} =\mathbf {Ax} }
m 차원 벡터 공간을 p 차원 벡터 공간으로 변환하는 선형 변환 B 역시
p
×
m
{\displaystyle p\times m}
B
{\displaystyle \mathbf {B} }
합성 한 결과인
B
∘
A
{\displaystyle B\circ A}
B
A
{\displaystyle \mathbf {BA} }
결합법칙 은 행렬 곱셈 § 결합법칙 에서 다룰 것이다.
연립 일차 방정식 의 일반항은 다음과 같이 쓸 수 있다.
a
11
x
1
+
⋯
+
a
1
n
x
n
=
b
1
a
21
x
1
+
⋯
+
a
2
n
x
n
=
b
2
⋮
a
m
1
x
1
+
⋯
+
a
m
n
x
n
=
b
m
{\displaystyle {\begin{matrix}a_{11}x_{1}+\cdots +a_{1n}x_{n}=b_{1}\\a_{21}x_{1}+\cdots +a_{2n}x_{n}=b_{2}\\\vdots \\a_{m1}x_{1}+\cdots +a_{mn}x_{n}=b_{m}\end{matrix}}}
위의 여러 방정식들을 행렬을 사용하면 다음과 같이 방정식 한 개로 간단히 나타낼 수 있다.
A
x
=
b
{\displaystyle \mathbf {Ax} =\mathbf {b} }
행렬 곱셈은 일반적인 산술적 곱셈 과 비슷한 성질을 가지지만, 첫째 행렬의 열 갯수와 둘째 행렬의 행 갯수가 동일할 때에만 정의된다는 특징이 있다. 또한 행렬 곱셈이 정의될 때에도 교환법칙 이 항상 성립하는 것은 아니라는 점에서 차이가 있다.[ 12] [ 13] [ 14]
A
B
≠
B
A
{\displaystyle {AB}\neq {BA}}
하지만 특수한 조건을 만족하는 경우에는 교환법칙이 성립한다. 다음과 같은 조건을 만족할 때 행과 열의 개수가 같은 정사각행렬 A와 B에 대해 곱셈의 교환법칙이 성립한다.
A
+
B
=
A
B
{\displaystyle A+B=AB}
A
B
=
B
A
{\displaystyle AB=BA}
행렬 곱셈은 결합법칙 이 성립한다:
(
A
B
)
C
=
A
(
B
C
)
{\displaystyle (\mathbf {AB} )\mathbf {C} =\mathbf {A} (\mathbf {BC} )}
[ 증명 1] 행렬
A
=
[
a
b
]
{\displaystyle A={\begin{bmatrix}a\\b\end{bmatrix}}}
B
=
[
c
d
]
{\displaystyle B={\begin{bmatrix}c&d\end{bmatrix}}}
A
B
=
[
a
b
]
[
c
d
]
=
[
a
c
a
d
b
c
b
d
]
{\displaystyle AB={\begin{bmatrix}a\\b\end{bmatrix}}{\begin{bmatrix}c&d\end{bmatrix}}={\begin{bmatrix}ac&ad\\bc&bd\end{bmatrix}}}
A
T
B
T
=
[
a
b
]
[
c
d
]
=
a
c
+
b
d
{\displaystyle A^{T}B^{T}={\begin{bmatrix}a&b\end{bmatrix}}{\begin{bmatrix}c\\d\end{bmatrix}}=ac+bd}
B
A
=
[
c
d
]
[
a
b
]
=
c
a
+
d
b
{\displaystyle BA={\begin{bmatrix}c&d\end{bmatrix}}{\begin{bmatrix}a\\b\end{bmatrix}}=ca+db}
B
T
A
T
=
[
c
d
]
[
a
b
]
=
[
c
a
c
b
d
a
d
b
]
{\displaystyle B^{T}A^{T}={\begin{bmatrix}c\\d\end{bmatrix}}{\begin{bmatrix}a&b\end{bmatrix}}={\begin{bmatrix}ca&cb\\da&db\end{bmatrix}}}
행렬
A
=
[
a
b
c
d
]
{\displaystyle A={\begin{bmatrix}a&b\\c&d\end{bmatrix}}}
B
=
[
e
f
g
h
]
{\displaystyle B={\begin{bmatrix}e&f\\g&h\end{bmatrix}}}
A
B
=
[
a
b
c
d
]
[
e
f
g
h
]
=
[
a
e
+
b
g
a
f
+
b
h
c
e
+
d
g
c
f
+
d
h
]
{\displaystyle AB={\begin{bmatrix}a&b\\c&d\end{bmatrix}}{\begin{bmatrix}e&f\\g&h\end{bmatrix}}={\begin{bmatrix}ae+bg&af+bh\\ce+dg&cf+dh\end{bmatrix}}}
↑
각각 m × n n × p p × q m × q
(
(
A
B
)
C
)
i
j
=
∑
r
=
1
p
(
∑
s
=
1
n
A
i
s
B
s
r
)
C
r
j
=
∑
s
=
1
n
A
i
s
(
∑
r
=
1
p
B
s
r
C
r
j
)
=
(
A
(
B
C
)
)
i
j
{\displaystyle \scriptstyle ((\mathbf {AB} )\mathbf {C} )_{ij}=\sum _{r=1}^{p}\left(\sum _{s=1}^{n}A_{is}B_{sr}\right)C_{rj}=\sum _{s=1}^{n}A_{is}\left(\sum _{r=1}^{p}B_{sr}C_{rj}\right)=(A(BC))_{ij}}
↑ “Comprehensive List of Algebra Symbols” . 《Math Vault》 (미국 영어). 2020년 3월 25일. 2020년 9월 6일에 확인함 . ↑ Nykamp, Duane. “Multiplying matrices and vectors” . 《Math Insight》. 2020년 9월 6일에 확인함 . ↑ O’Connor, John J.; Robertson, Edmund F. “Jacques Philippe Marie Binet” . 《MacTutor History of Mathematics Archive》 (영어). 세인트앤드루스 대학교 . ↑ Lerner, R. G.; Trigg, G. L. (1991). 《Encyclopaedia of Physics》 2판. VHC publishers. ISBN 978-3-527-26954-9 ↑ Parker, C. B. (1994). 《McGraw Hill Encyclopaedia of Physics》 2판. ISBN 978-0-07-051400-3 ↑ Lipschutz, S.; Lipson, M. (2009). 《Linear Algebra》. Schaum's Outlines 4판. McGraw Hill (USA). 30–31쪽. ISBN 978-0-07-154352-1 ↑ Riley, K. F.; Hobson, M. P.; Bence, S. J. (2010). 《Mathematical methods for physics and engineering》 . Cambridge University Press. ISBN 978-0-521-86153-3 ↑ Adams, R. A. (1995). 《Calculus, A Complete Course》 3판. Addison Wesley. 627쪽. ISBN 0-201-82823-5 ↑ Horn, Johnson (2013). 《Matrix Analysis》 2판. Cambridge University Press. 6쪽. ISBN 978-0-521-54823-6 ↑ “Comprehensive List of Algebra Symbols” . 《Math Vault》 (미국 영어). 2020년 3월 25일. 2020년 9월 6일에 확인함 . ↑ Nykamp, Duane. “Multiplying matrices and vectors” . 《Math Insight》. 2020년 9월 6일에 확인함 . ↑ Weisstein, Eric W. “Matrix Multiplication” . 《mathworld.wolfram.com》 (영어). 2020년 9월 6일에 확인함 . ↑ Lipcshutz, S.; Lipson, M. (2009). 〈2〉. 《Linear Algebra》. Schaum's Outlines 4판. McGraw Hill (USA). ISBN 978-0-07-154352-1 ↑ Horn, Johnson (2013). 〈0〉. 《Matrix Analysis》 2판. Cambridge University Press. ISBN 978-0-521-54823-6