스칼라 (수학)

스칼라(scalar)는 선형대수학에서 선형공간을 정의 할 때, 선형공간의 원소와 스칼라 곱을 하는 체의 원소이다. 예를 들어, 1차 실수 계수 다항식들의 선형공간 $\{a+bx|a,b\in \mathbb {R} \}$에서 스칼라는 실수이다.

정의

스칼라의 정의는 N차원 공간에서 N의 0승개의 수로 표현할 수 있는 물리량이다.

그러므로 좌표계가 변환되어도 그에 따라 변화하지 않는 양이라는 것이다. 예를 들어 속도 벡터가 두 개의 성분을 가지고 있다고 할 때(x축 방향으로 100 km/h, y축 방향으로 0 km/h) 각각의 성분은 크기만을 가지고 있지만 스칼라는 아니다. 왜냐하면 그 속도를 나타내기 위한 좌표계가 바뀌면 각각의 성분도 바뀌기 때문이다(예를 들어 x'축 방향으로 80 km/h, y'축 방향으로 60 km/h 라는 식으로).

좌표계가 변함에 따라 벡터의 각 성분은 바뀐다.
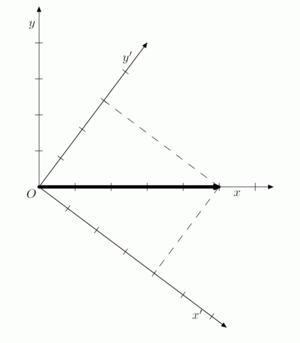
그러나 벡터의 크기는 스칼라이고 좌표계가 변해도 그 값은 불변이다. 이 그림에서 (x,y) 로 표현되는 좌표계에서 굵은 선으로 표시한 벡터의 성분은 (5,0)이지만, 벡터 자체가 변하지 않음에도 좌표계가 (x', y')으로 바뀌었을 때 각 성분은 (4,3)으로 바뀌었다.
하지만 두 좌표계에서 벡터${\overrightarrow {v}}$의 크기는 $||{\overrightarrow {v}}||={\sqrt {x^{2}+y^{2}}}={\sqrt {x'^{2}+y'^{2}}}=5$로 불변이고 따라서 스칼라이다.

하지만 막대의 길이가 1 m이면 어느 좌표계에서 재어도 1 m가 될 것이다. 따라서 막대의 길이는 스칼라이다(단 상대론적으로 움직이는 좌표계는 논외로 한다). 수학에서도 스칼라는 비슷한 의미를 가진다. 전산학에서는 스칼라를 단순히 '하나의 수'를 가리키는 말로 쓰기도 한다.

유래

스칼라(scalar)라는 말은 '사다리'를 뜻하는 라틴어 scala의 형용사형인 scalaris에서 따온 것이다. 이 용어를 수학에서 처음으로 쓴 사람은 프랑수아 비에트로, 그의 저서 《해석학입문_{In artem analyticem isagoge}》(1591년)에 쓰였다.

Magnitudines quae ex genere ad genus sua vi proportionaliter adscendunt vel descendunt, vocentur Scalares

규모의 본연과 어울려 어떤 하나에서 다른 하나로 비례적으로 상승하거나 하락하는 규모를 스칼라라고 한다.

한편 옥스포드 영어사전에 따르면 영어에서 이를 처음 쓴 사람은 윌리엄 로언 해밀턴으로, 1846년에 사원수의 실수부에 관한 내용을 서술하면서 사용하였다.

영어: The algebraically real part may receive, according to the question in which it occurs, all values contained on the one scale of progression of numbers from negative to positive infinity; we shall call it therefore the scalar part.

(대수적인 실수부는, 관련된 문제에 따라 음의 무한대에서 양의 무한대까지의 전 범위에 걸친 하나의 척도(scale)에 속하는 어느 값이든 가질 수 있다. 따라서 이 부분을 '스칼라 부'라고 부르기로 하겠다.)

해밀턴의 용례는 사원수 표기를 염두에 두고 쓴 것으로, 회전을 하나의 스칼라(사원수의 실수부)로 표현하고 벡터를 나머지 세개의 허수부로 표현하는 것이다.

같이 보기

• 스칼라곱
• 의사스칼라
• 텐서
• 스칼라웨이브
• 스칼라파

참고

• http://mathworld.wolfram.com/Vector.html
• http://mathworld.wolfram.com/Scalar.html