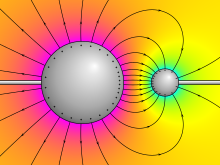
전위 (電位 , electric potential ) 또는 정전 퍼텐셜 (영어 : electrostatic potential )은 시간에 따라 변하지 않는 전기장 에서 단위 전하가 가지게 되는 전기적 위치 에너지 다. 국제단위계 에서 단위는 볼트 다.
맥스웰 방정식에 따르면
∇
×
E
=
−
∂
B
∂
t
{\displaystyle \nabla \times E=-{\frac {\partial B}{\partial t}}}
E
{\displaystyle E}
회전 이 0이 되므로 이를 어떤 스칼라함수의 기울기 로 표현할 수 있다. 보통 그 스칼라 함수를
−
V
{\displaystyle -V}
V
{\displaystyle V}
E
=
−
∇
V
{\displaystyle E=-\nabla V}
위치 에너지 가 절대적인 값이 아니라, 두 지점 사이의 위치 에너지 차이만이 절대적인 값인 것처럼, 전위 또한 상대적인 값이다. 즉 특정 지점의 전위는 임의로 정의할 수 있고, 두 지점의 전위차 만이 물리적 의미를 갖는다. (전위차는 전압 이라고도 불린다.) 수학적인 이유는
V
{\displaystyle V}
V
+
a
{\displaystyle V+a}
E
=
−
∇
V
=
−
∇
(
V
+
a
)
{\displaystyle E=-\nabla V=-\nabla \left(V+a\right)}
다만, 이론 물리학에서는 통상적으로 계에서 "무한히 먼 곳"에서의 전위를 0으로 놓는다. 전기 회로 에서는 보통 접지 (接地, ground )의 전위를 0으로 놓거나, 아니면 회로도에 어느 점의 전위를 0으로 정의하는지 표시한다.
전위는 에너지와 전하의 비(단위전하가 가지고 있는 정전기 퍼텐셜 에너지)이다. 즉, 전위의 국제 단위 인 볼트 는 다음과 같다.
볼트(V) = 줄 (J)/쿨롱 (C).
Δ
V
=
V
f
−
V
i
=
U
f
q
−
U
i
q
=
Δ
U
q
{\displaystyle \Delta V=V_{f}-V_{i}={U_{f} \over q}-{U_{i} \over q}={\Delta U \over q}}
Δ
V
=
V
A
−
V
B
=
Δ
U
q
0
=
−
∫
B
A
E
→
⋅
d
s
→
{\displaystyle \Delta V=V_{A}-V_{B}={\Delta U \over q_{0}}=-{\int _{B}^{A}{{\vec {E}}\cdot d{\vec {s}}}}}
V
=
U
q
0
{\displaystyle V={U \over q_{0}}}
V
f
−
V
i
=
−
∫
i
f
E
→
⋅
d
s
→
{\displaystyle V_{f}-V_{i}=-{\int _{i}^{f}{{\vec {E}}\cdot d{\vec {s}}}}}
두 점의 전위차(
V
f
−
V
i
{\displaystyle V_{f}-V_{i}}
보존장 이기 때문에 적분구간의 모양은 상관 없고, 적분구간의 시작점과 끝점만 중요하다.
하나의 점전하에 의해 생기는 전위 [ 편집 ]
V
=
1
4
π
ϵ
0
q
r
{\displaystyle V={1 \over 4\pi \epsilon _{0}}{q \over r}}
아무것도 없는 공간에 존재하는 점전하 q가 있을 때, 이 전하에서 r만큼 떨어진 곳의 전위는 위의 공식과 같이 정의할 수 있다.
이 공식은 무한히 먼 곳의 전위를 0V라고 놓은 다음에 세운 공식이다.
ϵ
0
{\displaystyle \epsilon _{0}}
유전율 여러 점전하에 의해 생기는 전위 [ 편집 ]
V
=
∑
i
=
1
n
V
i
=
1
4
π
ϵ
0
∑
i
=
1
n
q
i
r
i
{\displaystyle V=\sum _{i=1}^{n}V_{i}={1 \over 4\pi \epsilon _{0}}\sum _{i=1}^{n}{q_{i} \over r_{i}}}
공간에 점전하 n개가 존재할때, 특정 지점의 전위는 위의 공식과 같이 구할 수 있다.
q
{\displaystyle q}
r
{\displaystyle r}
V
=
1
4
π
ϵ
0
p
cos
θ
r
2
{\displaystyle V={1 \over 4\pi \epsilon _{0}}{{p\cos \theta } \over r^{2}}}
연속적인 전하 분포 [ 편집 ]
V
=
∫
d
V
=
1
4
π
ϵ
0
∫
d
q
r
{\displaystyle V=\int _{}dV={1 \over 4\pi \epsilon _{0}}\int _{}{dq \over r}}
E
→
=
−
∇
V
{\displaystyle {\vec {E}}=-\nabla V}
V
=
−
∫
E
→
⋅
d
s
→
{\displaystyle V=-\int {\vec {E}}\cdot d{\vec {s}}}
대전입자 계의 전기 퍼텐셜 에너지 [ 편집 ]
U
=
W
=
q
2
V
=
1
4
π
ϵ
0
{\displaystyle U=W=q_{2}V={1 \over 4\pi \epsilon _{0}}}
같이 보기 [ 편집 ]