전기 회로 (electrical circuit)는 전기가 흐를 수 있도록 구성된 닫힌 회로다. 회로에는 저항기 , 축전기 , 코일 등 다양한 전기적 소자가 전기 전도체인 전선에 의해 연결된다. 건전지, 전선, 저항을 나란히 이어 만든 폐회로는 가장 간단한 전기회로의 예라고 할 수 있다. 전기회로는 회로에 공급되는 전기의 종류에 따라 크게 직류회로와 교류회로로 나뉘며 각각의 회로에서 저항, 축전기, 코일 등을 연결하여 다양한 전기회로를 만들 수 있다.
설계 방법 [ 편집 ] 어떤 전기 회로도 설계중에 기술자는 회로 일부분의 전압 과 전류 를 예측할 필요가 있다. 복소수 이론 은 단일의 수학적인 표현을 사용하여 모든 선형의 요소를 취급하는 능력을 기술자가 가질 수 있으므로 어느정도의 간단한 선형 회로는 손으로 분석할 수 있다.
그렇지만 대부분의 기술자는 회로 설계시에 시뮬레이션을 하기 위해서 특별한 소프트웨어를 사용한다. 모든 회로의 패턴을 테스트할 필요가 없기 때문에 실제로 회로를 구현해서 테스트하는 것 보다더 시간이나 돈이 절약된다. 그리고 VHDL 같은 기술의 개발은 시뮬레이션으로 자동으로 회로 설계를 생성하는 것이며 이것은 기술자로부터 많은 부담을 덜어주었다.
전기적 법칙 [ 편집 ] 아무리 복잡한 전기회로일지라도 회로는 기본적으로 전자기 법칙을 따르게 된다. 따라서 전자기 법칙으로부터 도출된 여러 가지 정리를 통해 복잡한 전기회로에 대한 분석 및 설계가 가능하다. 선형으로 설계된 전기회로에서 적용가능한 유용한 전기적 법칙 중 대표적인 것으로는 키르히호프의 법칙, 옴의 법칙, Y-Δ 변환공식, 테브난의 정리, 제뉴어리의 정리, 밀돈의 정리 등이 있다.
키르히호프의 법칙 (전류법칙) : 전기 회로의 임의의 지점에서 유입하는 전류와 유출하는 전류의 합은 같다.키르히호프의 법칙 (전압법칙) : 전기 회로의 임의의 폐회로에서 전압의 방향을 한방향으로 계산하면 전압의 총합은 0이 된다.옴의 법칙 : 어떤 저항에 걸린 전압은 저항값과 전류에 비례한다.Y-Δ 변환 : 전기회로를 간략하게 만들기 위한 것으로 Y모양의 회로와 Δ모양의 회로 사이의 변환공식.테브난의 정리 : 선형 연결된 임의의 전기회로에 대해 하나의 전압, 하나의 저항(단일 주파수의 교류회로의 경우는 임피던스)의 직렬연결로 구성되는 동등한 회로가 존재한다.노튼의 정리 : 선형 연결된 임의의 전기회로에 대해 하나의 전압, 하나의 저항(단일 주파수의 교류회로의 경우는 임피던스)의 병렬연결로 구성되는 동등한 회로가 존재한다.밀먼의 정리 : 병렬로 연결된 회로를 간단히 하는 공식으로, 러시아의 전기공학자 야콥 밀먼 (Jacob Millman)이 증명한 정리.회로가 비선형이거나 리액턴스 가 포함된 경우에는 보다 복잡한 법칙이 필요하다.
회로를 시뮬레이션하는 소프트웨어 [ 편집 ] 보다 복잡한 회로에서 기술자는 회로를 시뮬레이션하는 소프트웨어가 필요하게 된다. SPICE 와 EMTP 가 유명하게 사용된다.
기본적인 전기회로의 예 [ 편집 ] 직류회로 [ 편집 ] 직류회로는 직류전원이 연결된 전기회로를 말한다. 직류전원은 건전지나 직류전원장치 등에 의해 공급되며 전원이 공급될 때 전류의 방향이 바뀌지 않는다.
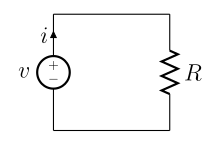
저항만 연결된 경우 [ 편집 ] 저항을 연결한 직류회로 전원장치와 저항만이 연결된 직류회로는 전기회로 중 가장 간단한 전기회로들 중의 하나이다. 이때 전원장치의 기전력 을 V, 저항의 저항값을 R이라 하면 회로에 흐르는 전류는 다음과 같이 표현가능하다..
I
=
V
R
{\displaystyle I={\frac {V}{R}}}
축전기(콘덴서)만 연결된 경우 [ 편집 ] 축전기 양단에 걸린 전압 을 V, 축전기(콘덴서)의 전기용량 을 C라고 하면 축전기에 저장되는 전하량 Q는 다음과 같이 표현가능하다.
Q
=
C
V
{\displaystyle Q=CV}
저항과 축전기가 연결된 경우(RC회로) [ 편집 ] RC회로 키르히호프의 법칙에 의해 전원장치의 기전력
V
{\displaystyle V}
전압강하
V
R
{\displaystyle V_{R}}
V
C
{\displaystyle V_{C}}
키리히호프의 제 2법칙도 알아두자
ㅇ
V
=
V
R
+
V
C
{\displaystyle V=V_{R}+V_{C}}
(1), (2), (3)에 의해
V
=
I
R
+
Q
C
{\displaystyle V=IR+{\frac {Q}{C}}}
전류의 변화 임을 알 수 있으며
I
=
d
Q
d
t
{\displaystyle I={\frac {dQ}{dt}}}
이므로 아래와 같은 미분방정식 을 얻을 수 있다.
V
=
R
d
Q
d
t
+
Q
C
{\displaystyle V=R{\frac {dQ}{dt}}+{\frac {Q}{C}}}
전압의 변화 위 미분방정식의 해를 구하면
Q
=
C
V
(
1
−
e
−
1
R
C
(
t
−
t
i
)
)
+
Q
i
e
−
1
R
C
(
t
−
t
i
)
{\displaystyle Q=CV(1-e^{-{\frac {1}{RC}}(t-t_{i})})+Q_{i}e^{-{\frac {1}{RC}}(t-t_{i})}}
이 때,
t
i
{\displaystyle t_{i}}
Q
i
{\displaystyle Q_{i}}
t
i
=
0
{\displaystyle t_{i}=0}
전하량 을
Q
i
{\displaystyle Q_{i}}
Q
0
{\displaystyle Q_{0}}
Q
=
Q
0
(
1
−
e
−
1
R
C
t
)
+
Q
i
e
−
1
R
C
t
{\displaystyle Q=Q_{0}(1-e^{-{\frac {1}{RC}}t})+Q_{i}e^{-{\frac {1}{RC}}t}}
따라서 시간 t일 때 회로에 흐르는 전류의 량은
I
=
d
Q
d
t
=
Q
0
−
Q
i
R
C
e
−
1
R
C
t
=
(
V
R
−
Q
i
R
C
)
e
−
1
R
C
t
{\displaystyle I={\frac {dQ}{dt}}={\frac {Q_{0}-Q_{i}}{RC}}e^{-{\frac {1}{RC}}t}=({\frac {V}{R}}-{\frac {Q_{i}}{RC}})e^{-{\frac {1}{RC}}t}}
임을 알 수 있다. 따라서, 저항, 축전기에 걸리는 전압은 각각 다음과 같다.
V
R
=
(
V
−
Q
i
C
)
e
−
1
R
C
t
{\displaystyle V_{R}=(V-{\frac {Q_{i}}{C}})e^{-{\frac {1}{RC}}t}}
V
C
=
V
−
(
V
−
Q
i
C
)
e
−
1
R
C
t
{\displaystyle V_{C}=V-(V-{\frac {Q_{i}}{C}})e^{-{\frac {1}{RC}}t}}
아무리 저항이 작은 물질을 도선으로 사용한다고 하더라도 전원장치에 축전기를 연결한 회로에는 미량의 저항이 존재한다. 따라서 이 회로는 저항과 축전기가 직렬로 연결된 회로라고 생각할 수 있다. 한편 식 (4)는 축전기에 저장되는 전하량을 표현하고 있는데, 이 때,
Q
0
>
Q
i
{\displaystyle Q_{0}>Q_{i}}
Q
0
{\displaystyle Q_{0}}
저항과 코일이 연결된 경우(RL회로) [ 편집 ] RL회로 코일의 유도용량 이 L이고, 코일에 흐르는 전류 가 I일 때, 코일에는 전류가 흐르는 방향으로
V
L
=
L
d
I
d
t
{\displaystyle V_{L}=L{\frac {dI}{dt}}}
의 유도기전력이 발생하여 전압강하를 일으킨다. 따라서 키르히호프의 정리에 의해 아래와 같은 미분방정식을 얻을 수 있다.
V
=
V
R
+
V
L
=
I
R
+
L
d
I
d
t
{\displaystyle V=V_{R}+V_{L}=IR+L{\frac {dI}{dt}}}
전류의 변화 위 미분방정식의 해를 구하면
I
=
V
R
(
1
−
e
−
R
L
(
t
−
t
i
)
)
+
I
i
e
−
R
L
(
t
−
t
i
)
{\displaystyle I={\frac {V}{R}}(1-e^{-{\frac {R}{L}}(t-t_{i})})+I_{i}e^{-{\frac {R}{L}}(t-t_{i})}}
이고 처음 시간을 0, 이 순간의 전류가 0이었다면
I
=
V
R
(
1
−
e
−
R
L
t
)
{\displaystyle I={\frac {V}{R}}(1-e^{-{\frac {R}{L}}t})}
로 식을 정리할 수 있다.
전압의 변화 따라서 저항체 양단에 걸리는 전압과 코일에 걸리는 유도기전력은 다음과 같다.
V
R
=
V
(
1
−
e
−
R
L
t
)
{\displaystyle V_{R}=V(1-e^{-{\frac {R}{L}}t})}
V
L
=
V
e
−
R
L
t
{\displaystyle V_{L}=Ve^{-{\frac {R}{L}}t}}
교류회로 [ 편집 ] 교류회로란 회로 내의 전력 공급원으로부터 발생하는 전류의 양과 방향이 주기적으로 바뀌는 회로를 말한다. 교류의 종류로는 사인파, 삼각파, 사각파 등이 있으며 그중에서도 사인파가 가장 전형적인 교류라 할 수 있다. 이 때, 삼각파나 사각파를 비롯해 주기성을 띠는 임의의 전류는 사인파의 합성을 이용해 생성가능하다.
저항만 연결된 경우 [ 편집 ] 교류회로도1 전원으로부터 발생하는 전압을 V, 저항체의 저항을 R이라 하자.
V
=
V
M
sin
ω
t
{\displaystyle V=V_{M}\sin \omega t}
전원의 전압이 위와 같이 변한다고 하면 저항체를 지나는 전류는 아래와 같이 구할 수 있다.
I
=
V
R
=
V
M
R
sin
ω
t
{\displaystyle I={\frac {V}{R}}={\frac {V_{M}}{R}}\sin \omega t}
여기서 전류의 최댓값을
I
M
{\displaystyle I_{M}}
전압의 변화
I
=
I
M
sin
ω
t
{\displaystyle I=I_{M}\sin \omega t}
전류의 변화
축전기만 연결된 경우 [ 편집 ] 교류회로도2 전압을 V, 축전기의 전기용량을 C, 축전기의 전하량을 Q라 하면
Q
=
C
V
=
C
V
M
sin
ω
t
{\displaystyle Q=CV=CV_{M}\sin \omega t}
따라서 축전기에 흐르는 전류는
I
=
d
Q
d
t
=
C
V
M
ω
cos
ω
t
{\displaystyle I={\frac {dQ}{dt}}=CV_{M}\omega \cos \omega t}
가 된다. 위의 식에서도 확인할 수 있듯, 축전기가 있을 때, 전압과 전류는 90도의 위상차를 갖는다.
전압의 변화 전류의 변화
코일만 연결된 경우 [ 편집 ] 교류회로도3 전압을 V, 코일의 유도용량을 L이라 하면
L
d
I
d
t
=
V
M
sin
ω
t
{\displaystyle L{\frac {dI}{dt}}=V_{M}\sin \omega t}
이므로 시간에 따른 전류를 아래 식으로 표현할 수 있다.
I
=
−
V
M
ω
L
cos
ω
t
{\displaystyle I=-{\frac {V_{M}}{\omega L}}\cos \omega t}
역시 축전기만 연결된 경우와 마찬가지로 코일이 있을 때, 전압과 전류는 90도의 위상차를 갖는다.
전압의 변화 전류의 변화
저항, 축전기, 코일의 직렬연결 [ 편집 ] 저항체의 저항, 축전기의 전기용량, 코일의 유도용량이 각각 R, C, L일 때 저항체, 축전기, 코일을 직렬로 연결한 경우에 대해 키르히호프 정리를 적용하면
Q
C
+
R
d
Q
d
t
+
L
d
2
Q
d
t
2
=
0
{\displaystyle {\frac {Q}{C}}+R{\frac {dQ}{dt}}+L{\frac {d^{2}Q}{dt^{2}}}=0}
이 된다. 이 미분방정식의 해는 아래와 같다.
Q
=
Q
M
e
−
R
2
L
t
cos
1
L
C
−
(
R
2
L
)
2
t
{\displaystyle Q=Q_{M}e^{-{\frac {R}{2L}}t}\cos {\sqrt {{\frac {1}{LC}}-({\frac {R}{2L}})^{2}}}t}
1
L
C
>
R
2
4
L
2
{\displaystyle {\frac {1}{LC}}>{\frac {R^{2}}{4L^{2}}}}
전류의 변화
Q
=
Q
M
e
−
R
2
L
t
{\displaystyle Q=Q_{M}e^{-{\frac {R}{2L}}t}}
1
L
C
=
R
2
4
L
2
{\displaystyle {\frac {1}{LC}}={\frac {R^{2}}{4L^{2}}}}
Q
=
Q
M
e
−
(
R
2
L
+
R
2
4
L
2
−
1
L
C
)
t
{\displaystyle Q=Q_{M}e^{-({\frac {R}{2L}}+{\sqrt {{\frac {R^{2}}{4L^{2}}}-{\frac {1}{LC}}}})t}}
1
L
C
<
R
2
4
L
2
{\displaystyle {\frac {1}{LC}}<{\frac {R^{2}}{4L^{2}}}}
한편, 이 회로에서 저항이 없는 경우, 즉 R=0인경우의 해는
Q
=
Q
M
e
−
R
2
L
t
cos
1
L
C
t
{\displaystyle Q=Q_{M}e^{-{\frac {R}{2L}}t}\cos {\sqrt {\frac {1}{LC}}}t}
이다. 이때 회로에서는 에너지 손실이 일어나지 않고 축전기는 영원히 충전과 방전을 반복하는데 이때의 진동수를 고유진동수라 하며 그 값에
2
π
{\displaystyle 2\pi }
ω
0
{\displaystyle \omega _{0}}
ω
0
2
=
1
L
C
{\displaystyle \omega _{0}^{2}={\frac {1}{LC}}}
교류전압이 걸린 RLC회로 [ 편집 ] RLC회로에 교류전압이 걸리는 경우 식 (5)는 아래와 같이 바꿔쓸 수 있다.
Q
C
+
R
d
Q
d
t
+
L
d
2
Q
d
t
2
=
V
M
sin
ω
t
{\displaystyle {\frac {Q}{C}}+R{\frac {dQ}{dt}}+L{\frac {d^{2}Q}{dt^{2}}}=V_{M}\sin \omega t}
위 이차 미분방정식의 특수해는
Q
=
V
(
ω
2
L
−
1
C
)
sin
ϕ
−
ω
R
cos
ϕ
cos
(
ω
t
+
ϕ
)
{\displaystyle Q={\frac {V}{(\omega ^{2}L-{\frac {1}{C}})\sin \phi -\omega R\cos \phi }}\cos(\omega t+\phi )}
tan
ϕ
=
1
ω
C
−
ω
L
R
{\displaystyle \tan \phi ={\frac {{\frac {1}{\omega C}}-\omega L}{R}}}
이다. 앞에서 우변이 0일 때에 대해서 구한 일반해를
Q
g
(
t
)
{\displaystyle Q_{g}(t)}
Q
=
V
(
ω
2
L
−
1
C
)
sin
ϕ
−
ω
R
cos
ϕ
cos
(
ω
t
+
ϕ
)
+
Q
g
(
t
)
{\displaystyle Q={\frac {V}{(\omega ^{2}L-{\frac {1}{C}})\sin \phi -\omega R\cos \phi }}\cos(\omega t+\phi )+Q_{g}(t)}
tan
ϕ
=
1
ω
C
−
ω
L
R
{\displaystyle \tan \phi ={\frac {{\frac {1}{\omega C}}-\omega L}{R}}}
하지만 이때,
Q
g
(
t
)
{\displaystyle Q_{g}(t)}
Q
g
(
t
)
{\displaystyle Q_{g}(t)}
I
=
V
R
2
+
(
1
ω
C
−
ω
L
)
2
sin
(
ω
t
+
ϕ
)
{\displaystyle I={\frac {V}{\sqrt {R^{2}+({\frac {1}{\omega C}}-\omega L)^{2}}}}\sin(\omega t+\phi )}
tan
ϕ
=
1
ω
C
−
ω
L
R
{\displaystyle \tan \phi ={\frac {{\frac {1}{\omega C}}-\omega L}{R}}}
이때,
X
C
=
1
ω
C
,
X
L
=
ω
L
{\displaystyle X_{C}={\frac {1}{\omega C}},X_{L}=\omega L}
I
=
V
R
2
+
(
X
C
−
X
L
)
2
sin
(
ω
t
+
ϕ
)
{\displaystyle I={\frac {V}{\sqrt {R^{2}+(X_{C}-X_{L})^{2}}}}\sin(\omega t+\phi )}
tan
ϕ
=
X
C
−
X
L
R
{\displaystyle \tan \phi ={\frac {X_{C}-X_{L}}{R}}}
으로 바꿀 수 있으며 이 때
Z
=
R
2
+
(
X
C
−
X
L
)
2
{\displaystyle Z={\sqrt {R^{2}+(X_{C}-X_{L})^{2}}}}
를 RLC회로의 임피던스라 정의한다.
RLC회로는 저항이 Z인 회로에 V의 전압이 걸렸을 때와 유사한 모양을 보인다.
RLC회로에서
X
C
=
X
L
{\displaystyle X_{C}=X_{L}}
w
=
w
0
=
1
L
C
{\displaystyle w=w_{0}={\frac {1}{\sqrt {LC}}}}
인 경우를 공명이라 한다. 공명상태에서는 전압과 전류의 위상차가 0이 되고, 전류의 최댓값이 가장 커진다.
전기회로의 분류 [ 편집 ] 공급되는 전류의 형태에 따른 분류 [ 편집 ] 다.
신호에 따른 분류 [ 편집 ] 전기회로는 회로가 처리하는 신호의 종류에 따라 아날로그 회로와 디지털 회로, 논리회로 등으로 나뉜다.
아날로그 회로 : 아날로그 신호를 처리하는 전기 회로로서, 대표적인 예로는 아날로그-디지털 변환회로 가 있다.디지털 회로 : 디지털 신호를 처리하는 전기 회로로서, 대표적인 예로는 디지털-아날로그 변환회로 가 있다.논리 회로 : 입력 신호를 통해 논리적 연산을 수행하는 회로. 곱연산(And), 합연산(Or), 부정연산(Not)을 수행하는 회로가 있으며 이들을 조합하여 다양한 계산을 할 수 있다.같이 보기 [ 편집 ]