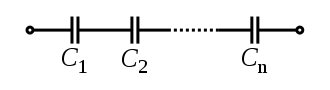축전기
이 문서의 내용은 출처가 분명하지 않습니다. (2011년 3월) |

축전기(capacitor 커패시터[*]) 또는 콘덴서(condenser)란 전기 회로에서 전기 용량을 전기적 퍼텐셜 에너지로 저장하는 장치이다. 두 개의 단자가 있는 수동소자이다. 축전기 내부는 두 도체판이 떨어져 있는 구조로 되어 있고, 사이에는 보통 절연체가 들어간다. 각 판의 표면과 절연체의 경계 부분에 전하가 비축되고, 양 표면에 모이는 전하량의 크기는 같지만 부호는 반대이다. 즉, 두 도체판 사이에 전압을 걸면 음극에는 (-)전하가, 양극에는 (+)전하가 유도되는데, 이로 인해 전기적 인력이 발생하게 된다. 이 인력에 의하여 전하들이 모여있게 되므로 에너지가 저장된다.
명칭[편집]
"콘덴서"(condenser)라는 이름은 일본에서 영문 이름을 번역한 것이 그대로 대한민국으로 유입된 것으로, 오늘날 한국물리학회 표준 용어는 "축전기"이다.[1] 뿐만 아니라, "condenser"라는 영어 용어는 광학에서 집광기(빛모으개)나 기체 역학에서 응축기(기체를 액체로 변화시키는 기구) 등 전혀 다른 기구를 일컫기도 한다.[2]
역사[편집]

1745년 최초의 축전기 형태인 라이덴병이 독일 발명가인 Ewald Georg von Kleist에 의하여 발명되었다. 1746년에는 네덜란드 라이덴 대학의 물리학자인 Pieter van Musschenbroek도 독자적으로 라이덴병을 발명하였다. 최초의 라이덴병은 운 유리병에 코르크 마개 중앙으로 도선을 삽입하여 물에 닿도록 한후 정전기를 충전시키는 단순한 형태였다. 그 후 유리병의 안과 밖에 금속박(주석박)을 입혀 극성이 서로 다른 전하를 충전시키고 도선을 서로 연결하여 충전된 전하를 방전시키는 완전한 형태의 콘덴서로 발전하게 되었다. 라이덴병에서 유리가 유전체, 주석박이 전극역할을 하고 있는 것이다.
그 후 지금과 같은 축전기가 비약적으로 발전하게 된 동기는 제2차 세계대전이 결정적인 고비가 되었다. 그 전에는 주로 자연적인 재료를 유전체로 사용하였으나 제2차 세계대전을 전후하여 독일에서 금속증착기술이 상용화되면서부터 소형화된 축전기의 출현이 가능하게 된 것이다.
축전기의 종류[편집]
축전기는 사용하는 유전체에 따라 공기 축전기·진공 축전기·가스입 축전기·액체 축전기·운모 축전기·종이 축전기·금속화종이 축전기·자기 축전기·유기막 축전기·전해 축전기 등으로 나눈다.
또 전기 용량이 변화하지 않는 고정 축전기와 변화하는 가변 축전기로도 분류한다. 가변 축전기는 흔히 바리콘이라고도 불리며 임피던스를 조절하여 전파를 수신하는데 사용된다.
이 밖에도, 용도에 따라 슈퍼 축전기 (용량이 매우 큰 축전기), 고압 축전기 (고압 전기를 축전할 때 사용, 대표적으로 테슬라 코일의 콘덴서로 사용하거나 카메라 플래시에서 순간적인 고전압을 발생 시킬 때 사용) 등으로 분류한다.
진공 축전기[편집]
진공 축전기(vacuum capacitor)란 유전체를 사용하지 않고 진공관과 같은 진공용기 속에 전극을 마주놓은 축전기이다. 진공 속에서는 글로방전이 발생하지 않고 대기 속의 습도·탄산가스 등의 영향이 없으므로 내전압(耐電壓)이 높고 안정하다. 따라서 전극 사이 거리를 좁힐 수 있으며, 소형으로 큰 용량을 얻을 수 있다. 또 높은 주파수라도 손실이 적고 안정하므로 송신기와 같은 고주파의 대전력에 적합하여 많이 사용한다. 구조는 고정용량형(동량형)과 가변용량형(가변형)이 있다. 대전력에 사용할 때는 축전기의 바깥쪽을 접지쪽으로 해서 사용하는 편이 좋다.
공기 축전기[편집]
공기 축전기(air capacitor)란 유전체로서 공기 자체를 사용하는 축전기이다. 밀봉하여 건조공기를 충전하면 시간에 따른 변화가 적으므로 이를 표준용으로 사용한다. 휴대용 이외의 라디오 AM수신기에 가변용량형 공기축전기가 사용된다. 얇은 판으로 된 금속극판이 공기 속의 음향으로 진동하면 두 금속판 사이 거리가 달라져 용량값이 변동한다. 이것을 억제하기 위해 보통 극판을 상호 결합해서 기계적 강도를 크게 한다.
금속화 종이 축전기[편집]
금속화 종이 축전기란 파라핀 등을 스며들게 한 얇은 종이의 한쪽 면에 아연·알루미늄 등의 금속을 높은 진공 속에서 증발시켜 부착시킨 금속화종이를 2장을 포개서 감은 축전기이다. MP콘덴서라고도 한다. 얇은 금속막이 전극이 되고 그 사이에 1장의 종이가 절연물로서 끼워져 여러 층으로 쌓인 구조의 축전기가 된다. 전극이 얇고 원통으로 감은 구조로 표면적이 넓어서 소형 축전기를 만들기 쉽다. 전자부품에 쓰는 원통형 축전기는 이 방식을 사용한다. 하지만 전극이 대단히 얇기 때문에 종이의 작은 구멍에서 절연파괴가 일어나기 쉽다.
전해 축전기[편집]
극성이 있으며, 띠 있는 쪽이 음극이다. 보통 용량과 정격전압이 숫자로 씌어 있다. 누설전류가 조금 있으며, 초고역에서의 주파수 특성이 좋지 않다.
마일러 축전기[편집]
유전체로 폴리에스테르 등이 사용된다. 일반적으로 다른 종류보다 저렴해서 많이 사용된다.
세라믹 축전기[편집]
크기가 작고 납작하며 유전체로 세라믹이 사용된다. 고주파를 잘 흐르게 하므로 고주파 필터에 사용될 수 있다. 일례로 RC 자동차 모터와 병렬로 연결하면 브러시로부터 발생하는 채터링을 접지로 보내는 역할을 하기 때문에 전파 간섭을 막을 수 있다.
탄탈륨 축전기[편집]
유전체로 탄탈럼 합금을 사용한 것. 전해 콘덴서와 유사하게 극성을 가지고 있으며, 비교적 쉽게 큰 용량을 만들수 있다. 특성은 전해 콘덴서보다 매우 뛰어나지만, 내압이 작다는 단점이 있다.
전기용량[편집]
평행한 축전기의 두 극판 사이의 거리가 일정할 때 양 극단에 걸린 전압 가 클수록 더 많은 전하량 가 대전되게 된다. 여기서 와 가 서로 비례관계에 있다는 것을 알 수가 있는데 여기서 는 이들 사이의 들어가는 비례상수로서 역할을 한다. 그래서 양 극단에 걸린 전압 가 같을 때 전기용량 가 클수록 더 많은 전하가 대전된다고 할 수 있고
라고 쓸 수 있다.
평행판 축전기[편집]
두 개의 평행한 판이 서로 평행하게 나란하게 있는 축전기를 평행판 축전기라고 한다. 평행판 축전기의 면적을 , 서로 떨어져 있는 거리를 라고 하며 두판에 모두 전하 와 가 대전되어 있다고 하면
식이 성립한다. 그리고
식이 성립하므로,이 식을 기존의 전기용량 식
에다가 대입하면
이 성립하게 되고 평행판에서의 전기용량
를 알 수가 있다.
원통형 축전기[편집]
원통형 축전기는 반지름이 다른 두개의 동축(同軸) 원통으로 구성된 축전기이다. 길이가 짧은 순서대로 각각 두 개의 동축 반지름을 , 라 하고 길이를 이라 할 때 길이 이 반지름 , 에 비해 매우 길다고 가정하면 가우스 법칙에 의해
이 성립한다. 이 식을 전기장 에 대해서 풀면
가 나오고
윗식을 사용해서 정리하면
를 얻는다.
를 얻는다.
구형 축전기[편집]
구형 축전기란 반지름이 서로 다른 두 구형껍질의 금속판으로 구성된 축전기다. 이 두 반지름 사이에 가우스 면을 잡으면
가 된다. 이 식을 다시 E에 대해서 풀면
나오고 위의 원통형 축전기와 마찬가지로 풀어보면
를 얻는다. 이제 Q=CV 이므로 C에 대해서 정리하면
처럼 전기용량을 구할 수 있다.
이 밖에도, 구면 하나로만 이루어진 "축전기"도 자기 전기 용량(self-capacitance)을 가지는데, 다음과 같다.
- .
여기서 는 구의 반지름이다.
축전기의 연결[편집]
직렬 연결[편집]
위의 그림과 같이 축전기가 직렬로 연결되어 있으면 각 축전기는 동일한 전하량을 갖는다. 왜냐하면 에 왼쪽 금속판에 (-)전지가 연결되어 있어 (-)전하를 띄면 의 오른쪽 판이 (+)전하를 띄게 되는데, 이 의 오른쪽 판이 왼쪽 금속판에 다시 (-)전하를 띄게 만들기 때문이다. 또한 각 축전기마다 동일한 전하를 가지고 있으므로 전체 축전기에 걸리는 전압은 각 축전기에 걸리는 전압의 합과 같다. 직렬 연결된 축전기의 합성 전기용량을 구해 보자, 먼저 각 축전기마다 동일한 전하량을 가지고 있으므로
이다. 전체 축전기의 전압은 세 축전기 전압의 합이므로
이고, 전체 합성 전기용량은
이것을 다시 풀어쓰면
가 나온다.
병렬 연결[편집]
위의 그림처럼 축전기가 병렬로 연결돼 있고 전지가 연결되어 있으면 각 축전기의 극판에 전지의 단자들이 모두 직접 연결되어 있다.그래서 각각의 축전기에는 동일한 전압 가 걸리게 되고 그에 따라 전하가 대전된다. 다시 정리하자면 병렬연결된 축전기에 전압 가 걸릴 때 전압 는 각 축전기에 동일하게 걸리고 축전기에 저장된 총 전하량은 각 축전기에 걸린 전하량의 합과 같다. 병렬 연결된 축전기의 합성 전기용량을 구해보자. 먼저, 각 축전기의 전하를 구하면
이다. 총전하량은 각 축전기의 걸린 전하량의 합이므로
이다. 그러므로 합성 전기용량은
로 쓸 수 있다.
축전기에 저장된 에너지[편집]
축전기에 저장된 전기적 위치 에너지를 구하기 위해서 대전되지 않은 하나의 축전기를 생각해보자. 대전되지 않은 축전기의 한 극판에서 다른 극판으로 전자를 옮긴다고 할 때는 일이 필요하다. 그런데 전하를 옮길 때마다 축전기에는 전기장이 생겨 점점 더 많은 일이 필요하게 된다. 어느 한 순간에 한 극판에서 다른 극판으로 전하량 를 옮긴다고 하자. 이때 양 극판의 전압차는 이고, 추가로 의 전하를 옮긴다고 하면 필요한 일은
이다. 그러므로 부터 까지 이동시키는데 한 일의 양은
이다. 이 일이 전기적 위치 에너지 U로 축전기에 저장되므로
이다. 전하 대신 전압 로 쓰면
이 된다.
같이 보기[편집]
각주[편집]
- ↑ 한국물리학회. “물리용어 조정안”. 2014년 7월 1일에 원본 문서에서 보존된 문서. 2010년 11월 6일에 확인함.
- ↑ “콘덴서”. 《표준국어대사전》. 국립국어원. 2020년 9월 28일에 확인함.