사각뿔
보이기
| 사각뿔 | |
|---|---|
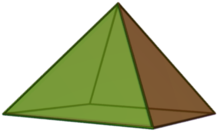 | |
| 종류 | 존슨 J92 – J1 – J2 |
| 면 | 삼각형 4개 사각형 1개 |
| 모서리 | 8 |
| 꼭짓점 | 5 |
| 꼭짓점 배치 | 4(32.4) (34) |
| 슐레플리 기호 | ( ) ∨ {4} |
| 대칭군 | C4v, [4], (*44) |
| 회전군 | C4, [4]+, (44) |
| 쌍대다면체 | 자신 |
| 특성 | 볼록 |
| 전개도 | |
 | |
기하학에서 사각뿔(四角-)은 밑면이 사각형인 각뿔이다. 꼭대기가 사각형의 중심의 수직 위에 있으면, 이것은 C4v 대칭을 가진다.
존슨의 다면체 (J1)
[편집]옆면이 모두 정삼각형이면, 각뿔은 존슨의 다면체중 하나이다(J1). 존슨의 다면체 92개는 1966년에 노만 존슨에 의해 이름이 붙여졌고 설명되었다.
존슨의 다면체는 정다각형 면을 가지지만 고른 다면체는 아닌 엄격히 볼록인 다면체 92개이다(즉, 플라톤 다면체, 아르키메데스의 다면체, 각기둥, 또는 엇각기둥이 아니다). 이것은 1966년에 이 다면체를 처음으로 나열한 노만 존슨의 이름을 따왔다.[1]
존슨 사각뿔은 변의 길이가 모두 a이라고 특성화 할 수 있다. 이 사각뿔의 높이 H (사각형의 중심에서 꼭대기까지), 표면적 A (모든 다섯 면을 포함), 그리고 부피 V는 다음과 같다:
다른 사각뿔
[편집]다른 사각뿔은 부등변삼각형 옆면을 가진다.
일반적인 밑면의 길이가 l이고 높이가 h인 사각뿔에 대해서, 표면적과 부피는 다음과 같다:
관련 다면체와 벌집
[편집]| 정각뿔 | ||||||
|---|---|---|---|---|---|---|
| 삼각 | 사각 | 오각 | 육각 | 칠각 | 팔각... | |
| 정다면체 | 등변 | 이등변 | ||||

|

|
|||||

|

|

|

|

|

| |
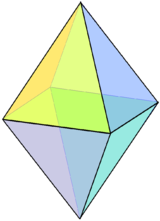
|

|
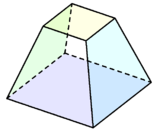
|
|---|---|---|
| 정팔면체는 사각쌍뿔로 생각할 수 있다. 즉 두존슨 사각뿔이 밑면끼리 붙은 것이다. | 사방육면체는 정육면체의 각 면에 짧은 사각뿔을 붙여서 만들 수 있다. | 사각 절두체는 꼭대기를 깎은 사각뿔이다. |
사각뿔은 정사면체, 깎은 정육면체 또는 육팔면체와 함께 공간을 채울 수 있다.[2]
쌍대 다면체
[편집]사각뿔은 위상적으로 자기쌍대 다면체이다. 쌍대 모서리 길이는 polar reciprocation 때문에 다르다.
| 사각뿔의 쌍대다면체 | 쌍대다면체의 전개도 |
|---|---|

|

|
위상
[편집]다른 모든 각뿔처럼, 사각뿔은 면의 개수와 같은 수의 꼭짓점을 가지는 자기쌍대 다면체이다.
사각뿔은 휠 그래프 W5로 나타낼 수 있다.
예시
[편집]
같이 보기
[편집]각주
[편집]- ↑ Johnson, Norman W. (1966), “Convex polyhedra with regular faces”, 《Canadian Journal of Mathematics》 18: 169–200, doi:10.4153/cjm-1966-021-8, MR 0185507, Zbl 0132.14603.
- ↑ http://woodenpolyhedra.web.fc2.com/JohnsonHoneycomb.pdf
외부 링크
[편집]- Weisstein, Eric Wolfgang. Square pyramid (Johnson solid). 《Wolfram MathWorld》 (영어). Wolfram Research.
- Weisstein, Eric Wolfgang. “Wheel graph”. 《Wolfram MathWorld》 (영어). Wolfram Research.
- Square Pyramid -- Interactive Polyhedron Model
- Virtual Reality Polyhedra www.georgehart.com: The Encyclopedia of Polyhedra (VRML model Archived 2012년 2월 18일 - 웨이백 머신)





