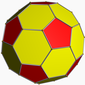
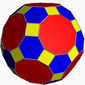
깎은 십이이십면체
| 깎은 십이이십면체 | |
|---|---|
 (클릭해서 회전하는 모델을 볼 수 있다) | |
| 종류 | 아르키메데스의 다면체 고른 다면체 |
| 성분 | F = 62, E = 180, V = 120 (χ = 2) |
| 면의 수{변의 수} | 30{4}+20{6}+12{10} |
| 콘웨이 표기법 | bD또는 taD |
| 슐레플리 기호 | tr{5,3}또는 |
| t0,1,2{5,3} | |
| 위토프 기호 | 2 3 5 | |
| 콕서터 다이어그램 | |
| 대칭군 | Ih, H3, [5,3], (*532), 120차 |
| 회전군 | I, [5,3]+, (532), 60차 |
| 이면각 | 6-10: 142.62° 4-10: 148.28° 4-6: 159.095° |
| 참조 | U28, C31, W16 |
| 특성 | 반정다면체 볼록 zonohedron |
 색칠된 면 |
 4.6.10 (꼭짓점 도형) |
 육방이십면체 (쌍대다면체) |
 전개도 |
깎은 십이이십면체는 아르키메데스의 다면체 중 하나이다. 면의 수가 62개이고 모서리만 무려 180개나 되며 꼭짓점의 수도 자그마치 120개이다. 깎인 정오각형 면과 깎인 정삼각형 면이 각각 정십각형, 정육각형 인 면이 생긴다. 마지막으로 깎인 면 역시 한 꼭짓점에 모이는 면 수처럼 정사각형 면이 생기게 된다.
| 이 글은 기하학에 관한 토막글입니다. 여러분의 지식으로 알차게 문서를 완성해 갑시다. |