둥근지붕
(둥근지붕 (기하학)에서 넘어옴)
| 둥근지붕의 집합 | |
|---|---|
 (예시: 오각둥근지붕) | |
| 면 | n각형 1개 2n각형 1개 오각형 n개 삼각형 2n개 |
| 모서리 | 7n |
| 꼭짓점 | 4n |
| 대칭군 | Cnv, [n], (*nn), 2n차 |
| 회전군 | Cn, [n]+, (nn), n차 |
| 특성 | 볼록 |
기하학에서 둥근지붕은 족 다면체이다. 이것은 지붕과 유사하지만 삼각형과 사각형이 번갈아 나타나는 것 대신에, 축을 중심으로 오각형과 삼각형이 번갈아 나타난다. 오각둥근지붕은 존슨의 다면체이다.
다른 형태들도 일그러진 등변오각형과 이면체 대칭으로 만들어질 수 있다.
다음은 둥근지붕과 관련된 고른 다면체의 설명이다.
오각둥근지붕과 관련된 고른 다면체:십이이십면체(삼각지붕으로 육팔면체를 만드는 것과 같이 밑면끼리 비틀어 붙임)
예시[편집]
| 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|
 삼각둥근지붕 |
 사각둥근지붕 |
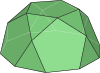 오각둥근지붕 |
 육각둥근지붕 |
 칠각둥근지붕 |
 팔각둥근지붕 |
같이 보기[편집]
참조[편집]
- Norman W. Johnson, "Convex Solids with Regular Faces", Canadian Journal of Mathematics, 18, 1966, pages 169–200. Contains the original enumeration of the 92 solids and the conjecture that there are no others.
- Victor A. Zalgaller (1969). 《Convex Polyhedra with Regular Faces》. Consultants Bureau. No ISBN. The first proof that there are only 92 Johnson solids.
| 이 글은 기하학에 관한 토막글입니다. 여러분의 지식으로 알차게 문서를 완성해 갑시다. |
