쌍각뿔
| 정 쌍각뿔의 집합 | |
|---|---|
 (육각형 형태를 예시로 들었다) | |
| 콕서터 다이어그램 | |
| 슐레플리 기호 | { } + {n} |
| 면 | 2n 삼각형 |
| 모서리 | 3n |
| 꼭짓점 | 2 + n |
| 면 배치 | V4.4.n |
| 대칭군 | Dnh, [n,2], (*n22), 4n차 |
| 회전군 | Dn, [n,2]+, (n22), 2n차 |
| 쌍대다면체 | n각기둥 |
| 특성 | 볼록, 면추이 |
| 전개도 | 
|

n각 쌍각뿔은 n각뿔과 그 거울상을 밑면에서 밑면끼리 연결하여 생긴 다면체이다. 쌍n각뿔은 2n개의 삼각형 면과 3n개의 모서리, 그리고 2 + n개의 꼭짓점을 가진다.
쌍각뿔의 이름에 쓰였던 n각형은 외부의 면이 아니라 내부의 면이다. 두 각뿔 절반을 연결하는 주 대칭면에 존재한다.
정-, 불규칙- 그리고 오목 쌍각뿔[편집]
정 쌍각뿔의 두 꼭짓점은 그 밑면의 중심의 위와 아래에 존재한다. 정 쌍각뿔이 아닌 쌍각뿔은 불규칙 쌍각뿔이라고 부른다. 정 쌍각뿔은 정다각형의 내부의 면을 가지고 대부분 직 쌍각뿔의 의미를 내포한다. 직 쌍각뿔은 내부의 다각형 P에 대해서 { } + P라고 나타낼 수 있고, 정 쌍n각뿔은 { } + {n}으로 나타낼 수 있다.
오목 쌍각뿔은 오목한 내부의 다각형을 가진다.
면추이 정 쌍각뿔은 고른 각기둥의 쌍대다면체이고, 일반적으로 이등변삼각형 면을 가진다.
구나 지구의에 쌍각뿔은 극에서 극으로 가는 n개의 등간격의 경도와 적도를 따라 이등분 하는 선으로 투영될 수 있다.
구면 삼각형으로 투영된 쌍각뿔 면들은 이면체 대칭 Dnh의 기본 영역을 나타낸다.
부피[편집]
쌍각뿔의 부피는 V =23Bh이며, B는 밑면의 넓이이고 h는 밑면에서 꼭대기 까지의 높이이다. 이 공식은 꼭대이의 위치에 관계없이, h가 밑면을 포함하는 평면에 수직한 거리로 측정되었으면 성립한다.
따라서 밑면이 변의 길이가 s인 정n각형으로 이루어졌고 높이가 h인 쌍각뿔의 부피는 다음과 같다:
정삼각형 쌍각뿔[편집]
세 종류의 쌍각뿔만이 모든 모서리의 길이가 같을 수 있다 (이것은 모든 면이 정삼각형이라는 것을 암시하며 따라서 쌍각뿔은 삼각형다면체이다): 삼각, 사각, 그리고 오각쌍뿔이다. 모서리의 길이가 동일한 삼각이나 오각쌍뿔은 존슨의 다면체(J12과 J13)로 계수되는 반면, 모서리의 길이가 동일한 사각쌍뿔, 또는 정팔면체는 플라톤의 다면체로 계수한다..

|

|

|
| 삼각쌍뿔 | 사각쌍뿔 (정팔면체) |
오각쌍뿔 |
Kalidescopic 대칭[편집]
밑면이 정다각형이고 꼭대기들을 통과하는 선이 밑면의 중심을 통과할 때, n각쌍뿔의 대칭군은 4n차의 이면체 대칭 Dnh를 가진다. 예외적으로 정팔면체의 경우는 더 큰 48차의 정팔면체 대칭군 Oh을 가지고 세 종류의 D4h을 부분군으로 가진다. 회전군은 2n차의 Dn를 가지고, 정팔면체는 더 큰 24차의 대칭군 O를 가지며 세 종류의 D4를 부분군으로 가진다.
구면 2n각쌍뿔의 이각형 면은 삼차원의 이면체 대칭의 기본 영역을 나타낸다: Dnh, [n,2], (*n22), 4n차. 반사 영역은 교대로 색칠된 삼각형을 거울상으로 볼 수 있다.
| D1h | D2h | D3h | D4h | D5h | D6h | ... |
|---|---|---|---|---|---|---|

|

|

|

|

|

|
직 정쌍각뿔[편집]
| 다면체 | 
|

|

|

|

|

| |||
|---|---|---|---|---|---|---|---|---|---|
| 콕서터 | |||||||||
| 타일링 | 
|

|

|

|

|

|

|

|

|
| 배치 | V2.4.4 | V3.4.4 | V4.4.4 | V5.4.4 | V6.4.4 | V7.4.4 | V8.4.4 | V9.4.4 | V10.4.4 |
부등변 다면체[편집]
부등변 다면체는 위상적으로 2n각쌍뿔과 같으나 동일한 부등변삼각형들로 이루어져있다.
두 종류가 존재하는데, 한 종류는 중심 주변의 2n개의 꼭짓점이 위아래로 교대된 고리를 이루고, 다른 종류는 꼭짓점 2n개는 같은 평면에 있지만 두 반지름이 교대되어있다.
첫 번째는 둘레에 있는 모서리의 중점의 2-fold 회전축과, 꼭짓점을 통한 대칭면, 그리고 그 축의 n-fold 회전대칭을 가지며, 대칭 Dnd, [2+,2n], (2*n), 2n차를 나타낸다. 결정학에서, 변이 8개와 12개가 있는 부등변다면체가 존재한다.[1] 이 모든 형태는 점추이이다.
두 번째는 대칭 Dn, [2,n], (*nn2), 2n차를 가진다.
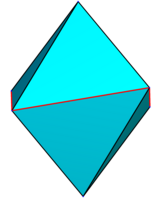
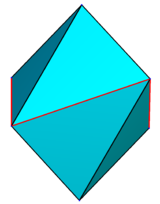
가장 작은 부등변다면체는 면이 8개이고 위상적으로 정팔면체와 동일하다. 두번째 종류는 마름모 쌍각뿔이다. 첫번째 종류는 (0,0,±1), (±1,0,z), (0,±1,−z)으로 나타나는 꼭짓점 6개를 가진다. 여기서 z는 0과 1사이의 변수이며, z = 0 일 때 정팔면체를 만들고, z = 1일 때는 동일한 면에 있는 면을 병합하면 맞붙인 쐐기꼴이 된다. z > 1일 때, 이것은 오목해진다.
| z = 0.1 | z = 0.25 | z = 0.5 | z = 0.95 | z = 1.5 |
|---|---|---|---|---|
|
|

|

|

|
별 쌍각뿔[편집]
자기 교차하는 쌍각뿔은 별 다각형을 중심도형으로 가져서 존재하고, 각각의 다각형 변을 이 두 점으로 연결하는 삼각형 면으로 정의되었다. {p/q} 쌍각뿔은 콕서터 다이어그램 ![]()
![]()
![]()
![]()
![]()
![]()
![]() 를 가진다.
를 가진다.
| 5/2 | 7/2 | 7/3 | 8/3 | 9/2 | 9/4 | 10/3 | 11/2 | 11/3 | 11/4 | 11/5 | 12/5 |
|---|---|---|---|---|---|---|---|---|---|---|---|
 |
면추이 짝수 변의 별은 다음 {8/3} 형태와 같이 비평면 지그재그형 꼭짓점, 안팎 변추이 형태, 또는 둘 다로 만들어질 수 있다:
| 정다각형 | 지그재그 정다각형 | 변추이 | 지그재그 변추이 |
|---|---|---|---|

|

|

|

|
참조[편집]
- ↑ “Crystal Form, Zones, Crystal Habit”. 《Tulane.edu》. 2017년 9월 16일에 확인함.
서지학[편집]
- Anthony Pugh (1976). 《Polyhedra: A visual approach》. California: University of California Press Berkeley. ISBN 0-520-03056-7. Chapter 4: Duals of the Archimedean polyhedra, prisma and antiprisms
외부 링크[편집]
- Weisstein, Eric Wolfgang. “Dipyramid”. 《Wolfram MathWorld》 (영어). Wolfram Research.
- Weisstein, Eric Wolfgang. “Isohedron”. 《Wolfram MathWorld》 (영어). Wolfram Research.
- Olshevsky, George. “Bipyramid”. 《Glossary for Hyperspace》. 2007년 2월 4일에 원본 문서에서 보존된 문서.
- The Uniform Polyhedra
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra


