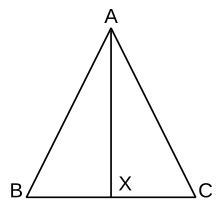
이등변 삼각형

기하학에서 이등변 삼각형(二等邊三角形, 영어: isosceles triangle)은 두 변의 길이가 같은 삼각형이다. 이 경우 길이가 같은 두 변이 마주보는 두 내각의 크기는 같다. 또한, 길이가 같은 두 변의 교점을 지나는 내각의 이등분선은 남은 한 변의 수직 이등분선과 일치한다. 길이가 같은 두 변이 마주보는 꼭짓점에서 두 변에 내린 수선과 중선, 내각의 이등분선의 길이는 세 변의 길이가 모두 같은 삼각형을 정삼각형이라고 한다. 과거 에우클레이데스의 정의에서는 이등변 삼각형을 정확히 두 변의 길이가 같은 삼각형으로 정의하여 정삼각형을 포함시키지 않았으나, 현대 기하학은 정삼각형을 이등변 삼각형의 특수한 경우로서 포함한다.
정의[편집]
삼각형의 두 변의 길이가 같다면, 이 삼각형을 이등변 삼각형이라고 한다. 이등변 삼각형의 길이가 같은 두 변을 등변(等邊, 영어: leg)이라고 하고, 남은 한 변을 밑변(-邊, 영어: base)이라고 한다. 두 등변 사이의 내각을 꼭지각(-角, 영어: vertex angle)이라고 부르며, 밑변과 등변 사이의 두 내각을 밑각(-角, 영어: base angle)이라고 부른다. 꼭지각이 예각·직각·둔각인 이등변 삼각형을 각각 예각 이등변 삼각형, 직각 이등변 삼각형, 둔각 이등변 삼각형이라고 한다. 세 변의 길이가 같은 삼각형을 정삼각형이라고 한다. 이는 예각 이등변 삼각형의 특수한 경우이다. 정삼각형에서는 임의의 변을 밑변으로 삼을 수 있다.
성질[편집]
밑변이 인 이등변 삼각형 의 다음과 같은 직선들은 서로 일치한다.
증명:
삼각형 의 밑변의 길이가 라고 하고 두 등변의 길이가 라고 할 때, 이 직선의 삼각형 내부에 포함된 부분의 길이는
이다.[1]:71, §2D
밑각[편집]
삼각형 에 대하여, 다음 두 조건이 서로 동치이다.[1]:7, §1B; 10, Exercise 1B.1
즉, 이등변 삼각형의 두 밑각의 크기는 같다. 이 명제를 당나귀의 다리라고 부르기도 한다. 반대로 크기가 같은 두 각의 대변의 길이는 같다.
증명:
증명:[1]:10, §1B
우선 가 성립한다고 가정하자. 그렇다면
이므로, 삼각형 와 는 SAS 합동에 따라 서로 합동이다. 특히, 가 성립한다.
이제 가 성립한다고 가정하자. 그렇다면
이므로, 삼각형 와 는 ASA 합동에 따라 서로 합동이다. 특히, 가 성립한다.
높이[편집]
삼각형 에 대하여, 다음 두 조건이 서로 동치이다.[1]:10, Exercise 1B.6, 1B.7; 20, §1E
- 를 지나는 의 수선 가 와 에서 만난다고 하고, 점 를 지나는 의 수선 가 와 에서 만난다고 할 때, 이다.
즉, 이등변 삼각형의 두 밑각의 꼭짓점에서 대변에 내린 수선의 길이는 같다. 반대로 두 꼭짓점에서 대변에 내린 수선의 길이가 같다면 이 두 대변의 길이는 같다.
증명:
우선 가 성립한다고 가정하자. 그렇다면
이므로, 삼각형 와 는 AAS 합동에 따라 서로 합동이다. 특히, 가 성립한다.
이제 가 성립한다고 가정하자. 그렇다면
이므로, 삼각형 와 는 AAS 합동에 따라 서로 합동이다. 특히, 가 성립한다.
중선[편집]
삼각형 에 대하여, 다음 두 조건이 서로 동치이다.[1]:10, Exercise 1B.4; 52, §2B, Problem 2.8
- 변 의 중점이 라고 하고, 변 의 중점이 라고 할 때, 이다.
즉, 이등변 삼각형의 두 밑각의 꼭짓점을 지나는 중선의 길이는 같다. 반대로 두 꼭짓점을 지나는 중선의 길이가 같다면 두 대변의 길이는 같다.
증명:
우선 가 성립한다고 가정하자. 그렇다면
이므로, 삼각형 와 는 SAS 합동에 따라 서로 합동이다. 특히, 가 성립한다.
이제 가 성립한다고 가정하자. 와 의 교점이 라고 하자. 그렇다면 는 삼각형 의 무게 중심이므로, 이고 이다. 따라서
이므로, 삼각형 와 는 SAS 합동에 따라 서로 합동이다. 특히, 이다. 따라서
이므로, 삼각형 와 는 AAS 합동에 따라 서로 합동이다. 특히, 가 성립한다.
각의 이등분선[편집]
슈타이너-레무스 정리에 따르면, 삼각형 에 대하여, 다음 두 조건이 서로 동치이다.[1]:10, Exercise 1B.5; 70, §2D, Problem 2.21
- 각 의 이등분선 가 와 에서 만난다고 하고, 각 의 이등분선 가 와 에서 만난다고 할 때, 이다.
즉, 이등변 삼각형의 두 밑각의 이등분선의 길이는 같다. 반대로 두 내각의 이등분선의 길이가 같다면 두 대변의 길이는 같다.
증명:
각의 이등분선의 길이의 제곱은
이다. 따라서 만약 라면 이고, 만약 라면 이고, 만약 라면 이다.
각주[편집]
외부 링크[편집]
- Weisstein, Eric Wolfgang. “Isosceles triangle”. 《Wolfram MathWorld》 (영어). Wolfram Research.