절두체

각뿔 절두체의 집합
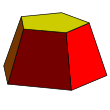예시: 오각과 사각뿔 절두체
면	사다리꼴 n개, n각형 2개
모서리	3n
꼭짓점	2n
대칭군	Cnv, [1,n], (*nn)
특성	볼록

기하학에서 절두체(frustum)는 입체(보통 원뿔이나 각뿔)를 절단하는 하나나 두 평행면 사이의 부분이다. 직 절두체는 직각뿔을 평행하게 깎은 것이다.

컴퓨터 그래픽스에서 뷰잉 프러스텀은 스크린에서 볼 수 있는 삼차원 영역이다. 이것은 잘라낸 각뿔으로 만들어진다; 특히, 절두체 컬링은 은면 검출의 방법이다.

항공 우주 산업에서, 절두체는 (세턴 V 같은) 두 단계의 다단계로켓 간의 깎은 원뿔 형태의 페어링이다.

모든 모서리의 길이를 같게 할 때, 절두체는 고른 각기둥이 된다.

원소, 특별한 경우, 그리고 관련 개념

사각뿔 절두체

정팔면체는 세 면에 정사면체를 붙여서 삼각 절두체로 만들 수 있다

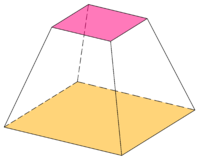
각 평면의 부분은 절두체의 바닥이나 밑면이다. 축이 있다면, 이것은 원본인 원뿔이나 각뿔의 축이다. 원형 밑면을 가지면 그 절두체는 원형이다; 축이 양 면에 수직하면 이것은 직 절두체이고 아니면 빗 절두체이다.

절두체의 높이는 두 밑면의 평면의 수직거리이다.

원뿔과 각뿔은 절단면이 꼭대기를 지나는(밑면이 점으로 줄어든) 절두체의 축퇴된 경우로 볼 수 있다. 각뿔 절두체는 기둥형 다면체의 부분 그룹이다.

두 절두체의 밑면을 붙이면 붙인 절두체를 만든다.

공식

부피

정사각뿔의 절두체의 부피 공식은 이집트 제13왕조(약 1850 BC)에 쓰인 모스크바 수학 파피루스라고 불리는 고대 이집트 수학에서 발견되었다:

$V={\frac {1}{3}}h(a^{2}+ab+b^{2}).$

여기서 a와 b는 깎은 각뿔의 밑면과 윗면의 변의 길이이고, h는 높이이다. 이집트인들은 깎은 정사각뿔의 부피를 얻는 공식을 알았지만, 모스크바 파피루스에서 주어진 이 공식에 대한 증명은 없다.

원뿔 또는 각뿔 절두체의 부피는 잘라내기 전의 입체의 부피에서 꼭대기의 부피를 뺀 것이다:

$V={\frac {h_{1}B_{1}-h_{2}B_{2}}{3}}$

이 때 B₁은 밑면의 넓이이고, B₂는 다른 밑면의 넓이이며, h₁, h₂는 꼭대기로부터 각각의 밑면까지의 수직거리이다.

다음을 고려하자

${\frac {B_{1}}{h_{1}^{2}}}={\frac {B_{2}}{h_{2}^{2}}}={\frac {\sqrt {B_{1}B_{2}}}{h_{1}h_{2}}}=\alpha$

부피의 공식은 비례 상수 α/3와 h₁과 h₂ 세제곱의 차의 곱 만으로 표현할 수 있다.

$V={\frac {h_{1}ah_{1}^{2}-h_{2}ah_{2}^{2}}{3}}={\frac {a}{3}}(h_{1}^{3}-h_{2}^{3})$

두 세제곱의 차를 인수분해 해서 ( a³ - b³ = (a-b)(a² + ab + b²) ) 절두체의 높이 h₁−h₂ = h를 얻을 수 있고 α(h₁² + h₁h₂ + h₂²)/3을 얻을 수 있다.

α를 분배하고 그 정의를 대입하면, 넓이 B₁과 B₂의 헤론 평균을 얻을 수 있다. 따라서 다른 공식은 다음과 같다:

$V={\frac {h}{3}}(B_{1}+{\sqrt {B_{1}B_{2}}}+B_{2})$

헤론은 이 식을 도출하는데 주목하고 그 가운데 마이너스 일의 제곱근인 허수와 마주하게 되었다.

특히, 원형 원뿔 절두체의 부피는 다음과 같다:

$V={\frac {\pi h}{3}}(R_{1}^{2}+R_{1}R_{2}+R_{2}^{2})$

여기서 π는 3.14159265...,이고 R₁, R₂는 두 밑면의 반지름이다.

각뿔 절두체.

밑면이 정n각형인 각뿔 절두체의 부피는 다음과 같다:

$V={\frac {nh}{12}}(a_{1}^{2}+a_{1}a_{2}+a_{2}^{2})\cot {\frac {\pi }{n}}$

여기서 a₁과 a₂는 두 밑면의 변의 수이다.

표면적

직원뿔 절두체에 대해서

${\begin{aligned}{\text{옆 면 표 면 적}}&=\pi (R_{1}+R_{2})s\\&=\pi (R_{1}+R_{2}){\sqrt {(R_{1}-R_{2})^{2}+h^{2}}}\end{aligned}}$

이고

${\begin{aligned}{\text{총 표 면 적}}&=\pi ((R_{1}+R_{2})s+R_{1}^{2}+R_{2}^{2})\\&=\pi ((R_{1}+R_{2}){\sqrt {(R_{1}-R_{2})^{2}+h^{2}}}+R_{1}^{2}+R_{2}^{2})\end{aligned}}$

이 때, R₁과 R₂는 각각 밑면과 윗면의 반지름이고, s는 절두체의 모선 길이이다.

밑면이 닯은 n각형인 직 절두체의 표면적은 아래와 같다:

$A={\frac {n}{4}}\left[(a_{1}^{2}+a_{2}^{2})\cot {\frac {\pi }{n}}+{\sqrt {(a_{1}^{2}-a_{2}^{2})^{2}\sec ^{2}{\frac {\pi }{n}}+4h^{2}(a_{1}+a_{2})^{2}}}\right]$

여기서 a₁과 a₂는 두 밑면의 변의 개수이다.

예시

• 미국 1달러 지폐의 뒷면에, 미국의 국장 반대편에 전시안이 그려진 각뿔 절두체가 나타난다.
• 일부 고대 아메리카 원주민의 둑은 각뿔의 절두체 모양을 하고 있다.
• 중국의 피라미드.
• 일리노이주의 시카고에 있는 존 핸콕 센터는 밑면이 직사각형인 절두체이다.
• 워싱턴 기념탑은 좁은 정사각형을 밑면으로 하는 절두체 위에 작은 각뿔을 올린 것이다.
• 3D 컴퓨터 그래픽스의 뷰잉 프러스텀은 각뿔 절두체로 모델링 된 가상 사진이나 비디오 카메라의 사용 가능한 시야이다.
• 스타니스와프 렘의 단편소설 모음집 The Cyberiad의 영어 번역본에서, 시 Love and tensor algebra에서는 claims that "모든 절두체는 원뿔을 갈망한다(every frustum longs to be a cone)"라고 주장하였다.
• 바구니와 특정한 전등갓은 원뿔 절두체의 일상적인 예시이다.
• 유리잔이나 어떤 우주 왕복선또한 그 예시이다.

참조

1.^ "frustum"이라는 용어는 조각, 단편이라는 뜻을 가지는 라틴어 frustum에서 왔다. 영어 단어는 종종 frustrum으로 철자를 틀리는데, 이 라틴어 단어는 영어 단어 "좌절하다(frustrate)"에 대응한다. 이 두 단어간의 혼동은 매우 오래되었다: 용어에 대한 주의는 Appendix Probi에서도 찾아볼 수 있고, 플라우투스의 작품에도 그에 관한 말장난이 있다.

외부 링크

• Derivation of formula for the volume of frustums of pyramid and cone (Mathalino.com)
• Weisstein, Eric Wolfgang. “Pyramidal frustum”. 《Wolfram MathWorld》 (영어). Wolfram Research. 
• Weisstein, Eric Wolfgang. “Conical frustum”. 《Wolfram MathWorld》 (영어). Wolfram Research. 
• Paper models of frustums (truncated pyramids)
• Paper model of frustum (truncated cone)
• Design paper models of conical frustum (truncated cones)