부분군
수학의 한 분야인 군론에서, 이항연산 ∗ 하에 주어진 군 G에 대하여, G의 부분집합 H 또한 이항연산 ∗ 하에서 군을 이룰 때, H를 G의 부분군이라고 한다. 더 정확히는, H가 G의 부분군이라는 것은 ∗의 H × H 에 대한 제한이 H에서의 군 연산인 것을 말한다. 이를 대개 H ≤ G로 나타내고, "H는 G의 부분군"이라고 읽는다.
임의의 군의 자명한 부분군은 항등원만을 갖고 있는 부분군 {e}이다.
군 G의 진부분군이란 G의 진부분집합인 부분군 H를 말한다. (즉, H ≠ G). 이를 대개 H < G로 나타내고 "H는 G의 진부분군"이라고 읽는다. 몇몇 저자들은 또한 자명한 군을 진부분군으로부터 제외하기도 한다 (즉, H ≠ {e}).
H가 G의 부분군일 때, 때때로 G를 H의 초군이라고 부른다.
보다 일반적으로 같은 정의를 G가 임의의 반군일 때도 적용하기도 하나, 이 글에서는 군의 부분군에 대해서만 다룰 것이다. 군 G가 때때로 순서쌍 (G, ∗)로 표기되는데, 대개 G가 다수의 대수적 또는 다른 구조들을 가지고 있을 때 연산 ∗를 강조하기 위함이다.
부분군의 기본 성질[편집]
- 군 G의 부분집합 H가 부분군일 필요충분조건은 H가 공집합이 아니고 곱과 역원에 대해 닫혀 있는 것이다. (닫혀 있다는 조건은 다음을 의미한다: a와 b가 H의 원소이면, ab와 a−1 또한 H의 원소이다. 이 두 조건은 하나의 동치 조건으로 결합될 수 있다: a와 b가 H의 원소이면, ab−1 또한 H의 원소이다.) H가 유한집합인 경우에, H가 부분군일 필요충분조건은 H가 곱에 대해 닫혀 있는 것이다. (이 경우에, H의 모든 원소는 H의 유한순환부분군을 생성하고, a의 역원은 n이 a의 위수일 때, a−1 = an−1)
- 위의 조건은 준동형사상의 용어로 서술될 수 있다; 즉, H가 G의 부분군일 필요충분조건은 H가 G의 부분집합이고 H에서 G로의 준동형인 포함사상이 존재하는 것이다. (즉, 모든 a에 대하여 i(a) = a)
- 부분군의 항등원은 군의 항등원이다: G가 항등원 eG,를 갖는 군이고 H가 항등원 eH,를 갖는 부분군이면, eH = eG.
- 부분에서의 원소의 역원은 군에서의 원소의 역원이다: H가 G의 부분군이고, a와 b가 ab = ba = eH,를 만족하는 H의 원소이면, ab = ba = eG.
- 부분군 A와 B의 교집합은 다시 부분군이다. 부분군 A와 B의 합집합이 부분군일 필요충분조건은 A와 B 중 하나가 다른 것을 포함할때인데, 예를 들어 2와 3은 2Z와 3Z의 합집합의 원소이나 그들의 합인 5는 그렇지 않다. 또다른 예는 평면에서 (덧셈 연산을 가지는) x축과 y축의 합집합이다. 이는 또한 교집합이 정확히 항등원인 두 부분군의 예이기도 하다.
- S가 G의 부분집합이면, S를 포함하는 가장 작은 부분집합이 존재하는데, 이는 S를 포함하는 모든 부분군의 교집합을 취해 찾을 수 있다; 이를 ⟨S⟩로 쓰고 S에 의하여 생성된 부분군이라고 부른다. G의 원소가 ⟨S⟩에 있을 필요충분조건은 이것이 S의 원소의 유한곱이고 그들의 역원일 때이다.
- G의 모든 원소 a는 순환부분군 ⟨a⟩를 생성한다. 만일 ⟨a⟩가 적당한 양의 정수 n에 대하여 Z/nZ 와 동형이면, n은 an = e가 되는 최소의 양의 정수이고, n을 a의 위수라고 부른다. ⟨a⟩가 Z와 동형이면, a는 무한 위수를 갖는다고 부른다.
- 임의의 주어진 군의 부분군들은 포함관계 하에 완비 격자를 이루는데, 이를 부분군 격자도라 부른다. (여기서 하한은 보통의 집합론적 교집합이나, 부분군의 집합의 상한은 부분군의 집합론적 합집합에 의하여 생성된 부분군이지, 이 자체의 집합론적 합집합이 아니다.) e가 G의 항등원이면, 자명한 부분군 {e}는 G의 부분군의 최소원이나, 부분군의 최대원은 G 자신이다.

잉여류와 라그랑주의 정리[편집]
주어진 부분군 H와 G의 원소 a에 대하여, 좌잉여류를 aH = {ah : h는 H의 원소}로 정의한다. a가 가역이므로, φ(h) = ah로 주어진 사상 φ : H → aH는 전단사이다. 더욱이, G의 모든 원소는 정확히 H의 좌잉여류 하나에 들어있다; 좌잉여류는 다음과 같이 정의된 동치관계에 대한 동치류이다. a1 ~ a2 라는 것은 a1−1a2 H의 원소인 것이다. H의 좌잉여류의 개수를 G에서의 H의 지수라 하고, [G : H]로 쓴다.
라그랑주의 정리는 유한군 G와 H에 대하여 다음을 진술한다.
여기서 |G| 와 |H|는 각각 G와 H의 위수를 가리킨다. 특히, G의 모든 부분군의 위수 (그리고 G의 모든 원소의 위수는) |G|의 약수여야 한다.[1]
우잉여류는 유사하게 Ha = {ha : h in H}로 정의한다. 이는 또한 적절한 동치관계에 대한 동치류들이고, 그들의 개수는 [G : H]와 같다.
만일 모든 G의 원소 a에 대하여 aH = Ha 이면, H를 정규부분군이라고 한다. 지수가 2인 모든 부분군은 정규부분군이다: 좌잉여류들과, 또한 우잉여류들이, 부분군이고 여집합이다. 더 일반적으로, p가 유한군 G의 위수를 나누는 가장 작은 소수이면, 지수 p를 갖는 임의의 부분군은 (만약 존재한다면) 정규부분군이다.
예: Z8의 부분군[편집]
G가 원소가 다음과 같은 순환군 Z8 이라고 하자.
그리고 이것의 군 연산은 법 8에 대한 덧셈이다. 이것의 케일리 표는
| + | 0 | 2 | 4 | 6 | 1 | 3 | 5 | 7 |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 2 | 4 | 6 | 1 | 3 | 5 | 7 |
| 2 | 2 | 4 | 6 | 0 | 3 | 5 | 7 | 1 |
| 4 | 4 | 6 | 0 | 2 | 5 | 7 | 1 | 3 |
| 6 | 6 | 0 | 2 | 4 | 7 | 1 | 3 | 5 |
| 1 | 1 | 3 | 5 | 7 | 2 | 4 | 6 | 0 |
| 3 | 3 | 5 | 7 | 1 | 4 | 6 | 0 | 2 |
| 5 | 5 | 7 | 1 | 3 | 6 | 0 | 2 | 4 |
| 7 | 7 | 1 | 3 | 5 | 0 | 2 | 4 | 6 |
이 군은 두 개의 비자명한 부분군을 갖는다: J={0,4} 와 H={0,2,4,6}, 여기서 J는 H의 부분군이기도 하다. H에 대한 케일리 표는 G에 대한 케일리 표의 왼쪽 위의 사분면이다. 군 G는 순환군이고, 이것의 모든 부분군도 그러하다. 일반적으로, 순환군의 부분군은 또한 순환군이다.
예: S4의 부분군 (4개의 원소 위의 대칭군)[편집]
모든 군은 주대각선 상의 중립 원소들만큼 작은 부분군을 갖는다:
자명한 군과 두 원소의 군인 Z2이다. 이 작은 부분군들은 다음 목록에서 세지 않는다.
 |
원소 12[편집]

부분군:





원소 8[편집]
 부분군:   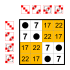 |
 부분군: 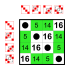  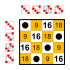 |
 부분군: 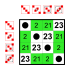  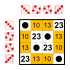 |
원소 6[편집]
 부분군:  |
 부분군:  |
 부분군:  |
 부분군:  |
원소 4[편집]
 |
 |
 |
 |
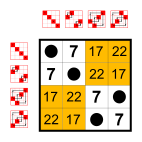 |
 |
 |
원소 3[편집]
 |
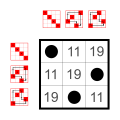 |
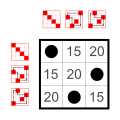 |
 |
다른 예[편집]
- 짝수 정수들은 정수의 덧셈군의 부분군이다: 두 개의 짝수를 더하면 짝수를 얻는다.
- 환 의 이데알은 덧셈군 의 부분군이다.
- 벡터공간의 선형 부분공간은 벡터의 덧셈군의 부분군이다.
- 를 아벨군이라 하자; 유한 주기를 갖는 의 원소들은 의 부분군을 형성하는데, 이를 의 꼬임 부분군이라 한다.
같이 보기[편집]
각주[편집]
- ↑ S., Dummit, David (2004). 《Abstract algebra》. Foote, Richard M., 1950- 3.판. Hoboken, NJ: Wiley. 90쪽. ISBN 9780471452348. OCLC 248917264.
참고 문헌[편집]
- Jacobson, Nathan (2009), Basic algebra, 1 (2nd ed.), Dover, ISBN 978-0-486-47189-1.
- Hungerford, Thomas (1974), Algebra (1st ed.), Springer-Verlag, ISBN 9780387905181.
- Artin, Michael (2011), Algebra (2nd ed.), Prentice Hall, ISBN 9780132413770.
- S., Dummit, David (2004). 《Abstract algebra》. Foote, Richard M., 1950- 3.판. Hoboken, NJ: Wiley. ISBN 9780471452348. OCLC 248917264.



![{\displaystyle [G:H]={|G| \over |H|}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e64b76d0605e6c7891273e65da28b5e431d4ea4)


