이 문서는 수학에서
리 대수 를 분류하는 벡터의 집합에 관한 것입니다.
식물학 에서 식물의 뿌리들의 구조에 대해서는
뿌리 문서를, 대한민국의 지명에 대해서는
근계리 문서를 참고하십시오.
예외 리 군 G2 의 근계.
α
{\displaystyle \alpha }
β
{\displaystyle \beta }
리 군 이론에서, 근계 (根系, 영어 : root system )는 일련의 기하학적 성질을 만족하는 유한 차원 벡터 의 집합 이다. 근계의 원소인 벡터는 근 (根, 영어 : root )이라고 부른다. 주어진 근계에 대하여 특정 성질을 만족하는 부분집합인 단순근 (單純根, 영어 : simple root )의 집합을 고를 수 있고, 이를 딘킨 도표 (영어 : Dynkin diagram )로 나타내어 분류할 수 있다. 반단순 리 군 에 근계를 대응시킬 수 있으며, 이를 통해 반단순 리 군들을 분류할 수 있다.
모든 근계는 기약 근계 (旣約根系, 영어 : irreducible root system )의 합으로 나타낼 수 있다. 기약 근계(의 동형류)는 복소수체 위의 단순 리 대수 (의 동형류)와 일대일로 대응한다.
유한 차원 실수 내적 공간
(
V
,
(
⋅
,
⋅
)
)
{\displaystyle (V,(\cdot ,\cdot ))}
Φ
⊆
V
{\displaystyle \Phi \subseteq V}
근계 라고 한다.
(선형 생성)
V
=
Span
R
Φ
{\displaystyle V=\operatorname {Span} _{\mathbb {R} }\Phi }
V
{\displaystyle V}
Φ
{\displaystyle \Phi }
선형 결합 으로 나타낼 수 있다. (이는 유일하지 않을 수 있다.)
(스칼라배의 제한)
α
∈
Φ
{\displaystyle \alpha \in \Phi }
−
α
∈
Φ
{\displaystyle -\alpha \in \Phi }
t
Φ
{\displaystyle t\Phi }
t
∈
R
{\displaystyle t\in \mathbb {R} }
Φ
{\displaystyle \Phi }
(반사에 대한 닫힘) 임의의
α
,
β
∈
Φ
{\displaystyle \alpha ,\beta \in \Phi }
α
{\displaystyle \alpha }
β
{\displaystyle \beta }
β
−
2
α
(
α
,
β
)
/
(
α
,
α
)
{\displaystyle \beta -2\alpha (\alpha ,\beta )/(\alpha ,\alpha )}
Φ
{\displaystyle \Phi }
(정수성)
0
∉
Φ
{\displaystyle 0\not \in \Phi }
∀
α
,
β
∈
Φ
:
2
(
α
,
β
)
/
(
α
,
α
)
∈
Z
{\displaystyle \forall \alpha ,\beta \in \Phi \colon 2(\alpha ,\beta )/(\alpha ,\alpha )\in \mathbb {Z} }
유한 집합 이다.근계의 원소는 근 이라고 부른다. 근계의 계수 (階數, 영어 : rank )는
V
{\displaystyle V}
두 실수 내적 공간
V
{\displaystyle V}
V
′
{\displaystyle V'}
Φ
⊆
V
{\displaystyle \Phi \subseteq V}
Φ
′
⊆
V
′
{\displaystyle \Phi '\subseteq V'}
f
(
Φ
)
=
Φ
′
{\displaystyle f(\Phi )=\Phi '}
전단사 실수 선형 변환
f
:
V
→
V
′
{\displaystyle f\colon V\to V'}
(
f
(
α
)
,
f
(
β
)
)
V
′
(
f
(
α
)
,
f
(
α
)
)
V
′
=
(
α
,
β
)
V
(
α
,
α
)
V
∀
α
,
β
∈
Φ
{\displaystyle {\frac {(f(\alpha ),f(\beta ))_{V'}}{(f(\alpha ),f(\alpha ))_{V'}}}={\frac {(\alpha ,\beta )_{V}}{(\alpha ,\alpha )_{V}}}\qquad \forall \alpha ,\beta \in \Phi }
라면,
(
V
,
Φ
)
{\displaystyle (V,\Phi )}
(
V
′
,
Φ
′
)
{\displaystyle (V',\Phi ')}
동형
특히, 동형이 등거리 변환 일 필요는 없다. 예를 들어, 항등 함수
(
V
,
(
−
,
−
)
)
→
(
V
,
2
(
−
,
−
)
)
{\displaystyle (V,(-,-))\to (V,2(-,-))}
노름 을
2
{\displaystyle {\sqrt {2}}}
1
{\displaystyle 1}
2
/
3
{\displaystyle {\sqrt {2/3}}}
통상적으로, 다음과 같은 표기를 사용한다.
⟨
α
,
β
⟩
=
2
(
α
,
β
)
(
α
,
α
)
{\displaystyle \langle \alpha ,\beta \rangle ={\frac {2(\alpha ,\beta )}{(\alpha ,\alpha )}}}
(이는 물론 쌍선형 형식 을 이루지 못한다.)
양근과 단순근 [ 편집 ] 근계
Φ
{\displaystyle \Phi }
양근의 집합 (陽根의 集合, 영어 : set of positive roots )
Φ
+
⊂
Φ
{\displaystyle \Phi ^{+}\subset \Phi }
임의의
α
∈
Φ
{\displaystyle \alpha \in \Phi }
α
∈
Φ
+
{\displaystyle \alpha \in \Phi ^{+}}
−
α
∈
Φ
+
{\displaystyle -\alpha \in \Phi ^{+}}
{
α
,
−
α
}
⊂
Φ
+
{\displaystyle \{\alpha ,-\alpha \}\subset \Phi ^{+}}
α
,
β
∈
Φ
+
{\displaystyle \alpha ,\beta \in \Phi ^{+}}
α
+
β
∈
Φ
{\displaystyle \alpha +\beta \in \Phi }
α
+
β
∈
Φ
+
{\displaystyle \alpha +\beta \in \Phi ^{+}}
양근의 집합의 원소를 양근 (陽根, 영어 : positive root )이라고 한다. 양근의 집합
Φ
+
⊆
Φ
{\displaystyle \Phi ^{+}\subseteq \Phi }
{
v
∈
V
:
∀
α
∈
Φ
:
α
∨
(
v
)
∈
Z
}
{\displaystyle \{v\in V\colon \forall \alpha \in \Phi \colon \alpha ^{\vee }(v)\in \mathbb {Z} \}}
위에 다음과 같은 부분 순서 를 줄 수 있다.
u
≤
v
⟺
∀
α
∈
Φ
+
:
α
∨
(
v
−
u
)
≥
0
{\displaystyle u\leq v\iff \forall \alpha \in \Phi ^{+}\colon \alpha ^{\vee }(v-u)\geq 0}
이 구성은 리 대수 의 표현론 에 등장하며, 이 경우 위의 격자는 정수 무게 의 격자에 해당한다.
단순근 [ 편집 ] 어떤 양근의 집합이 주어졌을 때, 단순근 (單純根, 영어 : simple root )은 두 양근의 합으로 나타낼 수 없는 근이다. 단순근들의 집합은
V
{\displaystyle V}
기저 를 이룬다.
카르탕 행렬 [ 편집 ] 근계
Φ
{\displaystyle \Phi }
단순근 의 열
α
1
,
…
,
α
r
{\displaystyle \alpha _{1},\dots ,\alpha _{r}}
카르탕 행렬 (영어 : Cartan matrix )
M
{\displaystyle M}
r
×
r
{\displaystyle r\times r}
정사각 행렬 이다.
M
=
(
M
i
j
)
i
,
j
=
1
,
…
,
r
{\displaystyle M=(M_{ij})_{i,j=1,\dots ,r}}
M
i
j
=
2
(
α
i
,
α
j
)
(
α
i
,
α
i
)
{\displaystyle M_{ij}=2{\frac {(\alpha _{i},\alpha _{j})}{(\alpha _{i},\alpha _{i})}}}
정의에 따라, 카르탕 행렬의 대각선 성분의 값은 모두 2이다.
카르탕 행렬이 주어지면, 이에 대응하는 근계 (및 복소수 반단순 리 대수 )를 재구성할 수 있다.
딘킨 도표 [ 편집 ] 기약근계의 딘킨 도표 각 근계
(
V
,
Φ
)
{\displaystyle (V,\Phi )}
딘킨 도표 (Дынкин圖表, 영어 : Dynkin diagram )라는, 일종의 유향 그래프 를 대응시킬 수 있다. 우선, 임의로
(
V
,
Φ
)
{\displaystyle (V,\Phi )}
Φ
+
⊆
Φ
{\displaystyle \Phi ^{+}\subseteq \Phi }
딘킨 도표는 각 단순근에 대응하는 꼭짓점 을 갖는다.
두 꼭짓점 사이에는 0개, 1개, 2개, 또는 3개의 변(邊)이 존재할 수 있다. 변이 2개 또는 3개인 경우, 변은 방향을 가지며, 이 방향은 항상 더 짧은 단순근을 가리킨다. (이 경우 두 단순근의 길이는 항상 다르다.)
두 꼭짓점 사이의 변의 수는 두 단순근 사이의 각도에 대응하며, 다음 표를 따른다.
근 사이 각 (라디안 )
근 사이 각 (°)
변의 종류
π
/
2
{\displaystyle \pi /2}
90°
변 없음
2
π
/
3
{\displaystyle 2\pi /3}
120°
하나의 변
3
π
/
4
{\displaystyle 3\pi /4}
135°
두 개의 변 + 화살표
5
π
/
6
{\displaystyle 5\pi /6}
150°
세 개의 변 + 화살표
딘킨 도표는 단순근의 선택에 관계없이 동일하다.
기약 근계의 딘킨 도표는 연결되어 있다. 딘킨 도표의 연결 성분 분해는 근계의 (기약 근계들로의) 직합 분해와 같다.
정수성 공리에 따라, 두 근 사이의 각은
π
/
2
{\displaystyle \pi /2}
π
/
3
{\displaystyle \pi /3}
π
/
4
{\displaystyle \pi /4}
π
/
6
{\displaystyle \pi /6}
근계의 정수성은 두 근 사이의 각들을 제한한다. 정수성 공리에 따라, 두 근 사이의 각의 코사인 은 정수의 제곱근의 반이어야 한다.
Z
∋
2
(
α
,
β
)
(
α
,
α
)
⋅
2
(
α
,
β
)
(
β
,
β
)
=
4
(
α
,
β
)
2
|
α
|
2
|
β
|
2
=
4
cos
2
(
θ
)
=
(
2
cos
(
θ
)
)
2
.
{\displaystyle \mathbb {Z} \ni 2{\frac {(\alpha ,\beta )}{(\alpha ,\alpha )}}\cdot 2{\frac {(\alpha ,\beta )}{(\beta ,\beta )}}=4{\frac {(\alpha ,\beta )^{2}}{\vert \alpha \vert ^{2}\vert \beta \vert ^{2}}}=4\cos ^{2}(\theta )=(2\cos(\theta ))^{2}.}
2
cos
(
θ
)
∈
[
−
2
,
2
]
{\displaystyle 2\cos(\theta )\in [-2,2]}
cos
θ
=
0
,
±
1
2
,
±
2
2
,
±
3
2
,
±
1
{\displaystyle \cos \theta =0,\pm {\tfrac {1}{2}},\pm {\tfrac {\sqrt {2}}{2}},\pm {\tfrac {\sqrt {3}}{2}},\pm 1}
이다. 즉,
θ
{\displaystyle \theta }
스칼라배 [ 편집 ] 근계
(
V
,
Φ
)
{\displaystyle (V,\Phi )}
t
∈
R
∖
{
0
}
{\displaystyle t\in \mathbb {R} \setminus \{0\}}
M
∈
O
(
V
;
R
)
{\displaystyle M\in \operatorname {O} (V;\mathbb {R} )}
(
V
,
t
M
Φ
)
{\displaystyle (V,tM\Phi )}
(
V
,
Φ
)
{\displaystyle (V,\Phi )}
두 근계
(
V
,
Φ
)
{\displaystyle (V,\Phi )}
(
V
′
,
Φ
′
)
{\displaystyle (V',\Phi ')}
직합
Φ
⊕
Φ
′
{\displaystyle \Phi \oplus \Phi '}
Φ
⊕
Φ
′
=
ι
(
Φ
)
∪
ι
′
(
Φ
′
)
{\displaystyle \Phi \oplus \Phi '=\iota (\Phi )\cup \iota '(\Phi ')}
V
→
ι
V
⊕
V
′
←
ι
′
V
′
{\displaystyle V{\xrightarrow {\iota }}V\oplus V'{\xleftarrow {\iota '}}V'}
여기서
ι
{\displaystyle \iota }
ι
′
{\displaystyle \iota '}
직합 의 정의에 등장하는 표준 포함 사상이다.
기약 근계 (旣約根系, 영어 : irreducible root system )는 두 (자명하지 않은) 근계의 합이 아닌, 자명하지 않은 근계다. 모든 근계는 기약 근계의 합으로 유일하게 나타낼 수 있다.
기약 근계의 근은 모두 길이가 같거나, 길이가 두 가지가 있다. 길이가 두 가지가 있을 경우는 긴 것은 긴 근 (영어 : long root ), 짧은 것은 짧은 근 (영어 : short root )으로 분류한다. (만약 길이가 모두 같다면, 모든 근이 긴 근이다.) 이 경우, 긴 근과 짧은 근의 노름 의 비는
2
{\displaystyle {\sqrt {2}}}
2
{\displaystyle {\sqrt {2}}}
1
{\displaystyle 1}
쌍대 근계 [ 편집 ] 근계
(
V
,
Φ
)
{\displaystyle (V,\Phi )}
쌍대 근계 (雙對根系, 영어 : dual root system )는 다음과 같다.
V
∨
{\displaystyle V^{\vee }}
V
{\displaystyle V}
쌍대 공간 이다. 물론, 내적을 사용하여 표준적인 동형 사상
V
→
V
∨
{\displaystyle V\to V^{\vee }}
Φ
∨
=
{
α
∨
:
α
∈
Φ
}
{\displaystyle \Phi ^{\vee }=\{\alpha ^{\vee }\colon \alpha \in \Phi \}}
임의의
u
,
v
∈
V
{\displaystyle u,v\in V}
u
∨
∈
V
∗
{\displaystyle u^{\vee }\in V^{*}}
u
∨
(
v
)
=
⟨
u
,
v
⟩
=
2
(
u
,
v
)
/
(
u
,
u
)
{\displaystyle u^{\vee }(v)=\langle u,v\rangle =2(u,v)/(u,u)}
그렇다면
(
V
∨
,
Φ
∨
)
{\displaystyle (V^{\vee },\Phi ^{\vee })}
임의의 근계
(
V
,
Φ
)
{\displaystyle (V,\Phi )}
(
V
∨
∨
,
Φ
∨
∨
)
{\displaystyle (V^{\vee \vee },\Phi ^{\vee \vee })}
단순 근계 가운데,
B
n
{\displaystyle B_{n}}
C
n
{\displaystyle C_{n}}
A
n
{\displaystyle A_{n}}
D
n
{\displaystyle D_{n}}
E
6
,
E
7
,
E
8
,
F
4
,
G
2
{\displaystyle E_{6},E_{7},E_{8},F_{4},G_{2}}
기약 근계의 목록 [ 편집 ] 기약 근계는 다음과 같이 분류한다. 고전 근계 (영어 : classical root system )는 네 개의 족
A
n
{\displaystyle A_{n}}
B
n
{\displaystyle B_{n}}
C
n
{\displaystyle C_{n}}
D
n
{\displaystyle D_{n}}
예외 근계 (영어 : exceptional root system )
G
2
,
F
4
,
E
6
,
E
7
,
E
8
{\displaystyle G_{2},F_{4},E_{6},E_{7},E_{8}}
고전군 (직교군 , 특수 유니터리 군 , 심플렉틱 군 )의 리 대수 (의 복소화)의 근계이나, 예외 근계는 그렇지 않다. 아래 표에서는 관례를 따라 긴 근의 길이가
2
{\displaystyle {\sqrt {2}}}
[1]
근계
근의 수
짧은 근 수
긴 근 부분격자의 지표
카르탕 행렬식
바일 군의 크기
콕서터 수
h
{\displaystyle h}
이중 콕서터 수
h
∨
{\displaystyle h^{\vee }}
딘킨 도표
콕서터 라벨[2] :43
이중 콕서터 라벨[2] :43
An n ≥ 1)
n (n + 1)
n + 1(n + 1)!
n
+
1
{\displaystyle n+1}
∙
−
∙
−
⋯
−
∙
{\displaystyle \bullet -\bullet -\cdots -\bullet }
1
−
1
−
⋯
−
1
{\displaystyle 1-1-\cdots -1}
Bn n ≥ 2)
2n 2
2n
2
2
2n n !
2
n
{\displaystyle 2n}
2
n
−
1
{\displaystyle 2n-1}
∙
−
∙
−
⋯
−
∙
⇒
∙
{\displaystyle \bullet -\bullet -\cdots -\bullet \Rightarrow \bullet }
1
−
2
−
⋯
−
2
⇒
2
{\displaystyle 1-2-\cdots -2\Rightarrow 2}
1
−
2
−
⋯
−
2
⇒
1
{\displaystyle 1-2-\cdots -2\Rightarrow 1}
Cn n ≥ 3)
2n 2
2n (n − 1)
2
2
2n n !
2
n
{\displaystyle 2n}
n
+
1
{\displaystyle n+1}
∙
−
∙
−
⋯
−
∙
⇐
∙
{\displaystyle \bullet -\bullet -\cdots -\bullet \Leftarrow \bullet }
2
−
2
−
⋯
−
2
⇐
1
{\displaystyle 2-2-\cdots -2\Leftarrow 1}
1
−
1
−
⋯
−
1
⇐
1
{\displaystyle 1-1-\cdots -1\Leftarrow 1}
Dn n ≥ 4)
2n (n − 1)
4
2n − 1n !
2
n
−
2
{\displaystyle 2n-2}
∙
−
∙
−
⋯
−
∙
<
∙
∙
{\displaystyle \bullet -\bullet -\cdots -\bullet <{\bullet \atop \bullet }}
1
−
2
−
⋯
−
2
<
1
1
{\displaystyle 1-2-\cdots -2<{1 \atop 1}}
E6 72
3
27 ×34 ×5
12
∙
−
∙
∙
−
∙
>
∙
−
∙
{\displaystyle {\bullet -\bullet \atop \bullet -\bullet }>\bullet -\bullet }
1
−
2
1
−
2
>
3
−
2
{\displaystyle {1-2 \atop 1-2}>3-2}
E7 126
2
210 ×34 ×5×7
18
∙
−
∙
∙
>
∙
−
∙
−
∙
−
∙
{\displaystyle {\bullet \atop {}}{- \atop {}}{\bullet \atop \bullet }>\bullet -\bullet -\bullet -\bullet }
2
−
3
2
>
4
−
3
−
2
−
1
{\displaystyle {2 \atop {}}{- \atop {}}{3 \atop 2}>4-3-2-1}
E8 240
1
214 ×35 ×52 ×7
30
∙
−
∙
∙
>
∙
−
∙
−
∙
−
∙
−
∙
{\displaystyle {\bullet \atop {}}{- \atop {}}{\bullet \atop \bullet }>\bullet -\bullet -\bullet -\bullet -\bullet }
2
−
4
3
>
6
−
5
−
4
−
3
−
2
{\displaystyle {2 \atop {}}{- \atop {}}{4 \atop 3}>6-5-4-3-2}
F4 48
24
4
1
27 ×32
12
9
∙
−
∙
⇒
∙
−
∙
{\displaystyle \bullet -\bullet \Rightarrow \bullet -\bullet }
2
−
3
⇒
4
−
2
{\displaystyle 2-3\Rightarrow 4-2}
2
−
3
⇒
2
−
1
{\displaystyle 2-3\Rightarrow 2-1}
G2 12
6
3
1
22 ×3
6
4
∙
⇛
∙
{\displaystyle \bullet \Rrightarrow \bullet }
2
⇛
3
{\displaystyle 2\Rrightarrow 3}
2
⇛
1
{\displaystyle 2\Rrightarrow 1}
고전적 기약 근계 [ 편집 ]
A
n
{\displaystyle A_{n}}
R
n
+
1
{\displaystyle \mathbb {R} ^{n+1}}
α
1
=
(
1
,
−
1
,
0
,
…
,
0
,
0
)
{\displaystyle \alpha ^{1}=(1,-1,0,\dots ,0,0)}
α
2
=
(
0
,
1
,
−
1
,
…
,
0
,
0
)
{\displaystyle \alpha ^{2}=(0,1,-1,\dots ,0,0)}
⋮
{\displaystyle \vdots }
α
n
=
(
0
,
0
,
…
,
1
,
−
1
)
{\displaystyle \alpha ^{n}=(0,0,\dots ,1,-1)}
B
n
{\displaystyle B_{n}}
α
1
=
(
1
,
−
1
,
0
,
…
,
0
,
0
)
{\displaystyle \alpha ^{1}=(1,-1,0,\dots ,0,0)}
α
2
=
(
0
,
1
,
−
1
,
…
,
0
,
0
)
{\displaystyle \alpha ^{2}=(0,1,-1,\dots ,0,0)}
⋮
{\displaystyle \vdots }
α
n
−
1
=
(
0
,
0
,
…
,
1
,
−
1
)
{\displaystyle \alpha ^{n-1}=(0,0,\dots ,1,-1)}
α
n
=
(
0
,
0
,
…
,
0
,
1
)
{\displaystyle \alpha ^{n}=(0,0,\dots ,0,1)}
C
n
{\displaystyle C_{n}}
α
1
=
(
1
,
−
1
,
0
,
…
,
0
,
0
)
{\displaystyle \alpha ^{1}=(1,-1,0,\dots ,0,0)}
α
2
=
(
0
,
1
,
−
1
,
…
,
0
,
0
)
{\displaystyle \alpha ^{2}=(0,1,-1,\dots ,0,0)}
⋮
{\displaystyle \vdots }
α
n
−
1
=
(
0
,
0
,
…
,
1
,
−
1
)
{\displaystyle \alpha ^{n-1}=(0,0,\dots ,1,-1)}
α
n
=
(
0
,
0
,
…
,
0
,
2
)
{\displaystyle \alpha ^{n}=(0,0,\dots ,0,2)}
D
n
{\displaystyle D_{n}}
α
1
=
(
1
,
−
1
,
0
,
…
,
0
,
0
)
{\displaystyle \alpha ^{1}=(1,-1,0,\dots ,0,0)}
α
2
=
(
0
,
1
,
−
1
,
…
,
0
,
0
)
{\displaystyle \alpha ^{2}=(0,1,-1,\dots ,0,0)}
⋮
{\displaystyle \vdots }
α
n
−
1
=
(
0
,
0
,
…
,
1
,
−
1
)
{\displaystyle \alpha ^{n-1}=(0,0,\dots ,1,-1)}
α
n
=
(
0
,
0
,
…
,
1
,
1
)
{\displaystyle \alpha ^{n}=(0,0,\dots ,1,1)}
예외적 기약 근계 [ 편집 ] 예외적 기약 근계는 E₆ , E₇ , E₈ , F₄ , G₂ 총 5개가 있다. 이들의 단순근들은 다음과 같다.
E8
1
-1
0
0
0
0
0
0
0
1
-1
0
0
0
0
0
0
0
1
-1
0
0
0
0
0
0
0
1
-1
0
0
0
0
0
0
0
1
-1
0
0
0
0
0
0
0
1
-1
0
0
0
0
0
0
1
1
0
-½
-½
-½
-½
-½
-½
-½
-½
F4
1
-1
0
0
0
1
-1
0
0
0
1
0
-½
-½
-½
-½
G2
2
/
3
{\displaystyle {\sqrt {2/3}}}
0
−
3
/
2
{\displaystyle -{\sqrt {3/2}}}
1
/
2
{\displaystyle 1/{\sqrt {2}}}
낮은 차원의 근계 [ 편집 ] 0차원 근계는 (자명하게) 하나 밖에 없다.
1차원 근계는 하나 밖에 없으며,
{
−
2
,
2
}
⊂
R
{\displaystyle \{-{\sqrt {2}},{\sqrt {2}}\}\subset \mathbb {R} }
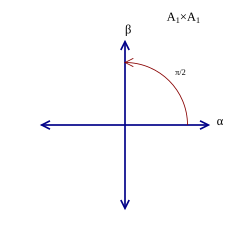
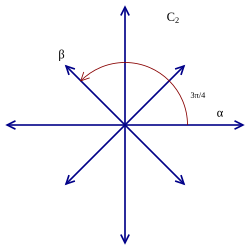
2차원 근계는 총 4개가 있으며, 이들 가운데 3개는 기약 근계이다. (아래 표에서,
B
2
{\displaystyle B_{2}}
C
2
{\displaystyle C_{2}}
A
1
×
A
1
{\displaystyle A_{1}\times A_{1}}
D
2
{\displaystyle D_{2}}
A
1
×
A
1
{\displaystyle A_{1}\times A_{1}}
A
2
{\displaystyle A_{2}}
B
2
{\displaystyle B_{2}}
C
2
{\displaystyle C_{2}}
D
2
{\displaystyle D_{2}}
G
2
{\displaystyle G_{2}}
3차원 기약 근계는 세 가지가 있으며, 이들은 정육면체 ·정팔면체 의 모양을 가진다.
반단순 리 대수에 대응되는 근계 [ 편집 ] 복소수체 위의 반단순 리 대수
g
{\displaystyle {\mathfrak {g}}}
카르탕 부분 대수
h
⊆
g
{\displaystyle {\mathfrak {h}}\subseteq {\mathfrak {g}}}
h
{\displaystyle {\mathfrak {h}}}
g
{\displaystyle {\mathfrak {g}}}
킬링 형식 을 통해 자연스럽게 유한 차원 실수 내적 공간 을 이룬다.
그렇다면,
g
{\displaystyle {\mathfrak {g}}}
딸림표현 에 대응하는
h
{\displaystyle {\mathfrak {h}}}
무게 들
Φ
=
{
α
∈
h
∨
:
g
α
≠
0
}
⊆
h
∨
{\displaystyle \Phi =\{\alpha \in {\mathfrak {h}}^{\vee }\colon {\mathfrak {g}}_{\alpha }\neq 0\}\subseteq {\mathfrak {h}}^{\vee }}
을 생각하자. 그렇다면,
(
h
∨
,
Φ
)
{\displaystyle ({\mathfrak {h}}^{\vee },\Phi )}
g
{\displaystyle {\mathfrak {g}}}
단순 리 대수 들로의 직합 분해는
(
h
∨
,
Φ
)
{\displaystyle ({\mathfrak {h}}^{\vee },\Phi )}
특히, 단순 리 대수 에 대응하는 근계는 기약 근계이다.
두 반단순 리 대수 가 서로 동형일 필요 충분 조건 은 그 대응하는 근계가 서로 동형인 것이다. 근계의 이론은 복소수 반단순 리 대수 의 표현론 에서 비롯하였다. 각 반단순 리 대수에는 근계를 대응시킬 수 있으며, 단순 리 대수 에 대응되는 근계는 기약 근계이다.
카르탕 행렬의 개념은 엘리 카르탕 이 도입하였다. 딘킨 도표의 개념은 예브게니 딘킨 이 도입하였다.
참고 문헌 [ 편집 ] Dynkin, E. B. The structure of semi-simple algebras. Uspehi Matem. Nauk (N.S.) 2, (1947). no. 4(20), 59–127. 외부 링크 [ 편집 ] 같이 보기 [ 편집 ]


























































![{\displaystyle 2\cos(\theta )\in [-2,2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a5c767297a7512c69089c0b49082c5623727b25)











































































