이항분포
확률 질량 함수
누적 분포 함수
매개변수
n
≥
0
{\displaystyle n\geq 0}
정수 )
0
≤
p
≤
1
{\displaystyle 0\leq p\leq 1}
실수 )
지지집합
k
∈
{
0
,
…
,
n
}
{\displaystyle k\in \{0,\dots ,n\}\!}
확률 질량
(
n
k
)
p
k
(
1
−
p
)
n
−
k
{\displaystyle {n \choose k}p^{k}(1-p)^{n-k}\!}
누적 분포
I
1
−
p
(
n
−
⌊
k
⌋
,
1
+
⌊
k
⌋
)
{\displaystyle I_{1-p}(n-\lfloor k\rfloor ,1+\lfloor k\rfloor )\!}
기댓값
n
p
{\displaystyle np\!}
중앙값 one of
{
⌊
n
p
⌋
,
⌈
n
p
⌉
}
{\displaystyle \{\lfloor np\rfloor ,\lceil np\rceil \}}
[1]
최빈값
⌊
(
n
+
1
)
p
⌋
{\displaystyle \lfloor (n+1)\,p\rfloor \!}
분산
n
p
(
1
−
p
)
{\displaystyle np(1-p)\!}
비대칭도
1
−
2
p
n
p
(
1
−
p
)
{\displaystyle {\frac {1-2p}{\sqrt {np(1-p)}}}\!}
첨도
1
−
6
p
(
1
−
p
)
n
p
(
1
−
p
)
{\displaystyle {\frac {1-6p(1-p)}{np(1-p)}}\!}
엔트로피
1
2
ln
(
2
π
n
e
p
(
1
−
p
)
)
+
O
(
1
n
)
{\displaystyle {\frac {1}{2}}\ln \left(2\pi nep(1-p)\right)+O\left({\frac {1}{n}}\right)}
적률생성함수
(
1
−
p
+
p
e
t
)
n
{\displaystyle (1-p+pe^{t})^{n}\!}
특성함수
(
1
−
p
+
p
e
i
t
)
n
{\displaystyle (1-p+pe^{it})^{n}\!}
이항 분포 (二項分布)는 연속된 n 번의 독립적 시행에서 각 시행이 확률 p를 가질 때의 이산 확률 분포 이다. 이러한 시행은 베르누이 시행이라고 불리기도 한다. 사실, n =1일 때 이항 분포는 베르누이 분포 이다.
이항 분포는 양봉 분포 (Bimodal distribution)와는 다른 것이다.
기본적인 예: 일반적인 주사위를 10회 던져서 숫자 6이 나오는 횟수를 센다. 이 분포는 n = 10이고 p = 1/6인 이항분포이다.
다른 예로는, 아주 많은 인구의 5%가 쌍꺼풀이 있다고 해보자. 그리고 100명을 무작위적으로 선택한다. 당신이 선택한 쌍꺼풀을 가진 사람의 수는 n = 100이고 p = 0.05인 이항분포를 따른다.
상세내용 [ 편집 ] 확률 질량 함수 [ 편집 ] 일반적으로, 확률변수 K 가 매개변수 n 과 p 를 가지는 이항분포를 따른다면, K ~ B(n ,p )라고 쓴다. n 번 시행 중에 k 번 성공할 확률은 확률 질량 함수 로 주어진다:
Pr
(
K
=
k
)
=
f
(
k
;
n
,
p
)
=
(
n
k
)
p
k
(
1
−
p
)
n
−
k
{\displaystyle \Pr(K=k)=f(k;n,p)={n \choose k}p^{k}(1-p)^{n-k}}
이 때, k = 0, 1, 2, ..., n 이고,
(
n
k
)
=
n
!
k
!
(
n
−
k
)
!
{\displaystyle {n \choose k}={\frac {n!}{k!(n-k)!}}}
는 이항 계수(C (n ,k ) 또는 n Ck 라고 쓰기도 함)이다. 이 식은 다음과 같이 이해할 수 있다: 우리는 k 번의 성공(p k n − k 번의 실패((1 − p )n − k k 번의 성공은 n 번의 시도 중 어디서든지 발생할 수 있고, 또한 k 번의 성공을 가지는 분포는 C(n , k )개가 있다.
이항 분포 확률에 대한 참고표를 만들 때, 표는 대체로 n /2개의 값으로 채워져 있다. 이것은 k > n /2에 대해 확률이 다음과 같이 계산될 수 있기 때문이다.
f
(
k
;
n
,
p
)
=
f
(
n
−
k
;
n
,
1
−
p
)
.
{\displaystyle f(k;n,p)=f(n-k;n,1-p).\,\!}
그러므로 다른 k 와 다른 p 를 보아야 한다(이항 분포는 일반적으로 대칭적이지 않음).
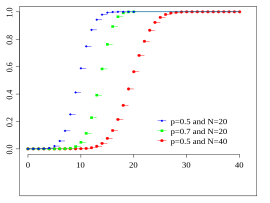
누적 분포 함수 [ 편집 ] 누적 분포 함수는 다음과 같이 베타함수꼴로 쓸 수 있다:
F
(
k
;
n
,
p
)
=
Pr
(
X
≤
k
)
=
I
1
−
p
(
n
−
k
,
k
+
1
)
{\displaystyle F(k;n,p)=\Pr(X\leq k)=I_{1-p}(n-k,k+1)\!}
이 때, k 는 정수이고, 0 ≤ k ≤ n 이다. 만약 x 가 정수일 필요가 없거나 양수일 필요가 없다면 다음과 같이 쓸 수 있다:
F
(
x
;
n
,
p
)
=
Pr
(
X
≤
x
)
=
∑
j
=
0
Floor
(
x
)
(
n
j
)
p
j
(
1
−
p
)
n
−
j
.
{\displaystyle F(x;n,p)=\Pr(X\leq x)=\sum _{j=0}^{\operatorname {Floor} (x)}{n \choose j}p^{j}(1-p)^{n-j}.}
k ≤ np 를 만족하는 k 에 대해에 대해 분포 함수의 낮은 꼬리에 대한 상계를 유도할 수 있다. 특히, 호에프딩 부등식을 이용하면 다음을 얻는다:
F
(
k
;
n
,
p
)
≤
exp
(
−
2
(
n
p
−
k
)
2
n
)
,
{\displaystyle F(k;n,p)\leq \exp \left(-2{\frac {(np-k)^{2}}{n}}\right),\!}
그리고 체르노프 부등식은 다음의 경계를 유도하는 데 사용할 수 있다:
F
(
k
;
n
,
p
)
≤
exp
(
−
1
2
p
(
n
p
−
k
)
2
n
)
.
{\displaystyle F(k;n,p)\leq \exp \left(-{\frac {1}{2\,p}}{\frac {(np-k)^{2}}{n}}\right).\!}
평균, 분산, 최빈값 [ 편집 ] 만약 X : B(n , p )라면, X 의 기댓값 은
E
(
X
)
=
n
p
{\displaystyle \operatorname {E} (X)=np\,\!}
이고 분산 은
Var
(
X
)
=
n
p
(
1
−
p
)
.
{\displaystyle \operatorname {Var} (X)=np(1-p).\,\!}
이것은 쉽게 증명할 수 있다. 먼저 한 번의 베르누이 시행을 생각해보자. 결과는 1과 0 두 가지이고, 1이 나올 확률이 p , 0이 나올 확률이 1 − p 이다. 이 시행의 평균은 μ = p 이다. 분산의 정의를 이용하면 다음을 얻는다.
σ
2
=
(
1
−
p
)
2
p
+
(
0
−
p
)
2
(
1
−
p
)
=
p
(
1
−
p
)
.
{\displaystyle \sigma ^{2}=\left(1-p\right)^{2}p+(0-p)^{2}(1-p)=p(1-p).}
이제 n 번의 시행에 대한 분산을 구한다고 생각해보자(일반적인 이항 분포). 각 시행은 독립이므로, 각 시행에 대한 분산들을 더하면
σ
n
2
=
∑
k
=
1
n
σ
2
=
n
p
(
1
−
p
)
.
{\displaystyle \sigma _{n}^{2}=\sum _{k=1}^{n}\sigma ^{2}=np(1-p).\quad }
X 의 최빈값은 (n + 1)p 와 같거나 작은 가장 큰 정수이다; 만약 m = (n + 1)p 이 정수라면, m − 1과 m 이 둘 다 최빈값이다.
평균과 분산의 명확한 유도 [ 편집 ] 명확한 유도를 위해 다음의 식을 이용한다.
∑
k
=
0
n
Pr
(
X
=
k
)
=
∑
k
=
0
n
(
n
k
)
p
k
(
1
−
p
)
n
−
k
=
1
{\displaystyle \sum _{k=0}^{n}\operatorname {Pr} (X=k)=\sum _{k=0}^{n}{n \choose k}p^{k}(1-p)^{n-k}=1}
먼저, 기댓값 의 정의를 적용하면
E
(
X
)
=
∑
k
x
k
⋅
Pr
(
x
k
)
=
∑
k
=
0
n
k
⋅
Pr
(
X
=
k
)
=
∑
k
=
0
n
k
⋅
(
n
k
)
p
k
(
1
−
p
)
n
−
k
{\displaystyle \operatorname {E} (X)=\sum _{k}x_{k}\cdot \operatorname {Pr} (x_{k})=\sum _{k=0}^{n}k\cdot \operatorname {Pr} (X=k)=\sum _{k=0}^{n}k\cdot {n \choose k}p^{k}(1-p)^{n-k}}
k 가 0이므로 첫 번째 항(k' = 0)은 0이다. 이것은 제외될 수 있으므로, 하한을 k = 1로 바꿀 수 있다.
E
(
X
)
=
∑
k
=
1
n
k
⋅
n
!
k
!
(
n
−
k
)
!
p
k
(
1
−
p
)
n
−
k
=
∑
k
=
1
n
k
⋅
n
⋅
(
n
−
1
)
!
k
⋅
(
k
−
1
)
!
(
n
−
k
)
!
⋅
p
⋅
p
k
−
1
(
1
−
p
)
n
−
k
{\displaystyle \operatorname {E} (X)=\sum _{k=1}^{n}k\cdot {\frac {n!}{k!(n-k)!}}p^{k}(1-p)^{n-k}=\sum _{k=1}^{n}k\cdot {\frac {n\cdot (n-1)!}{k\cdot (k-1)!(n-k)!}}\cdot p\cdot p^{k-1}(1-p)^{n-k}}
우리는 n 과 k 를 팩토리얼로부터 꺼냈고, p 를 하나 빼냈다.
E
(
X
)
=
n
p
⋅
∑
k
=
1
n
(
n
−
1
)
!
(
k
−
1
)
!
(
n
−
k
)
!
p
k
−
1
(
1
−
p
)
n
−
k
{\displaystyle \operatorname {E} (X)=np\cdot \sum _{k=1}^{n}{\frac {(n-1)!}{(k-1)!(n-k)!}}p^{k-1}(1-p)^{n-k}}
여기서 m = n - 1 이고, s = k - 1라고 하자.
E
(
X
)
=
n
p
⋅
∑
s
=
0
m
(
m
)
!
(
s
)
!
(
m
−
s
)
!
p
s
(
1
−
p
)
m
−
s
=
n
p
⋅
∑
s
=
0
m
(
m
s
)
p
s
(
1
−
p
)
m
−
s
{\displaystyle \operatorname {E} (X)=np\cdot \sum _{s=0}^{m}{\frac {(m)!}{(s)!(m-s)!}}p^{s}(1-p)^{m-s}=np\cdot \sum _{s=0}^{m}{m \choose s}p^{s}(1-p)^{m-s}}
이 합은 전체 이항 분포에 대한 합이다. 그러므로
E
(
X
)
=
n
p
⋅
1
=
n
p
{\displaystyle \operatorname {E} (X)=np\cdot 1=np}
분산을 다음과 같이 쓸 수 있다는 것은 증명할 수 있다:
Var
(
X
)
=
E
(
X
2
)
−
(
E
(
X
)
)
2
.
{\displaystyle \operatorname {Var} (X)=\operatorname {E} (X^{2})-(\operatorname {E} (X))^{2}.}
이 식을 사용하면 X 2 의 기댓값 역시 필요하다는 것을 알 수 있다. 이것은 다음과 같이 구할 수 있다.
E
(
X
2
)
=
∑
k
=
0
n
k
2
⋅
Pr
(
X
=
k
)
=
∑
k
=
0
n
k
2
⋅
(
n
k
)
p
k
(
1
−
p
)
n
−
k
.
{\displaystyle \operatorname {E} (X^{2})=\sum _{k=0}^{n}k^{2}\cdot \operatorname {Pr} (X=k)=\sum _{k=0}^{n}k^{2}\cdot {n \choose k}p^{k}(1-p)^{n-k}.}
이를 이용해 계산하면,
E
(
X
2
)
=
n
p
⋅
∑
s
=
0
m
k
⋅
(
m
s
)
p
s
(
1
−
p
)
m
−
s
=
n
p
⋅
∑
s
=
0
m
(
s
+
1
)
⋅
(
m
s
)
p
s
(
1
−
p
)
m
−
s
{\displaystyle \operatorname {E} (X^{2})=np\cdot \sum _{s=0}^{m}k\cdot {m \choose s}p^{s}(1-p)^{m-s}=np\cdot \sum _{s=0}^{m}(s+1)\cdot {m \choose s}p^{s}(1-p)^{m-s}}
(마찬가지로, m = n - 1 이고, s = k - 1로 치환). 합을 두 부분으로 나누면,
E
(
X
2
)
=
n
p
⋅
(
∑
s
=
0
m
s
⋅
(
m
s
)
p
s
(
1
−
p
)
m
−
s
+
∑
s
=
0
m
1
⋅
(
m
s
)
p
s
(
1
−
p
)
m
−
s
)
.
{\displaystyle \operatorname {E} (X^{2})=np\cdot {\bigg (}\sum _{s=0}^{m}s\cdot {m \choose s}p^{s}(1-p)^{m-s}+\sum _{s=0}^{m}1\cdot {m \choose s}p^{s}(1-p)^{m-s}{\bigg )}.}
첫 번째 항은 위에서 계산한 평균과 같다. 결과는 mp 이다. 두 번째 항은 1이다.
E
(
X
2
)
=
n
p
⋅
(
m
p
+
1
)
=
n
p
(
(
n
−
1
)
p
+
1
)
=
n
p
(
n
p
−
p
+
1
)
.
{\displaystyle \operatorname {E} (X^{2})=np\cdot (mp+1)=np((n-1)p+1)=np(np-p+1).}
이 결과와 평균(E(X ) = np )을 이용해서 분산을 다시 표시해보면 다음과 같다.
Var
(
X
)
=
E
(
X
2
)
−
(
E
(
X
)
)
2
=
n
p
(
n
p
−
p
+
1
)
−
(
n
p
)
2
=
n
p
(
1
−
p
)
.
{\displaystyle \operatorname {Var} (X)=\operatorname {E} (X^{2})-(\operatorname {E} (X))^{2}=np(np-p+1)-(np)^{2}=np(1-p).}
같이 보기 [ 편집 ]
↑ Hamza, K. (1995). The smallest uniform upper bound on the distance between the mean and the median of the binomial and Poisson distributions. Statist. Probab. Lett. 23 21–25.